一种风电场自适应最优惯量控制器设计

刘宏伟，谢雅雯，洪 昊，江奕军，王雅新，李宇骏，张建良

（1.国网杭州供电公司，浙江 杭州 310000；2.浙江大学 电气工程学院，浙江 杭州 310027；3.杭州电力设备制造有限公司，浙江 杭州 310004；4.西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

近年来，可再生能源发展迅速，特别是随着风电高渗透率接入电网，给系统稳定性带来了诸多挑战[1]，[2]。一方面是变速风机中使用的电力电子变换器解耦了风机转速和系统频率之间的关系，无法及时响应系统频率偏差[3]；另一方面，变速风机功率控制中经常采用最大功率跟踪（MPPT）算法，无法预留功率备用量，当风电功率与系统需求不平衡时，将对系统稳定性产生较大的影响[4]。为了将这种影响降到最低，关键是要挖掘并发挥风机的系统惯量支撑能力。

目前，通过变速风机进行系统惯量支撑主要有两种控制模式。第一种是调节风机叶片的桨距角改变风机出力，以预留功率备用来支撑系统频率[5]。这种方案迫使风机偏离MPPT工作点，不可避免地产生风能损失问题。此外，桨距角响应相对较慢，且控制系统的频繁激活也会增加风机的机械应力和疲劳损耗。第二种是通过设计惯量控制器，调节风机转子转速参与系统频率调节[6]～[8]。然而，惯量控制也必然会偏离MPPT运行点，造成风能捕获能力的下降。为了更好地支撑系统频率，同时尽可能减少风能捕获的损失，选取合适的下垂控制系数将是惯量控制的重要工作[9]。

在传统的惯量控制方法中，每台风机被简单地设置为具有相同的下垂控制系数，以平均分担系统功率偏差量。然而，由于风电场中尾流效应的影响，不同风机所面临的有效风速是不同的，处于上风向的前排风机所面临的有效风速将远大于下风向的后排风机。因此，当发生系统过频干扰事件时，转速较高的前排风机通过转速提升而降低出力的潜在能力将远远小于转速较低的后排风机。在传统方案中通常配合采用桨距角控制以降低前排风机出力，从而不可避免地导致风电场总体风能 捕 获 能 力 的 下 降[6]，[7]。

本文以含双馈感应风机（DFIG）的风电场参与系统支撑为背景，将风电场的惯量支撑问题建模为风机转速的优化问题，并根据最优转速自适应调整惯量控制器的下垂增益参数，实现系统的惯量支撑能力，同时最大限度地减少对风能捕获的影响。通过仿真表明，相比于采用相同下垂增益的传统惯量控制方案，本文方案在有效提供系统功率支撑的同时，能够为风电场捕获更多的风能。

1 传统惯量控制策略

1.1 双馈感应风机模型

DFIG从风中汲取的机械功率为

式中:ρ为空气密度；R为风轮机的叶片半径；Vw为风速；λ为叶尖速比；Cp为风能利用系数，与桨距角β和λ有关。

式中:δ为参数。

式中:ωB为风机叶片的转速；ω0为风机转子的转速；kg为风机叶片和转子之间的齿轮传动比。

根据式（1），在DFIG稳定运行的情况下，若不考虑风机损耗，则:

根据MPPT算法可得:

式中:Cpmax为最优风能利用系数；KG为功率与转速间的关系系数。当DFIG运行于非MPPT点，由式（2）可知，Cp是一个高阶非线性表达式，用多项式对Cp进行拟合，可得:

式中:aj为第j次项的系数；D为拟合的多项式最高次数。

风机i的输出有功功率为

1.2 传统惯量控制模型

DFIG功率调节主要通过MPPT和桨距角控制共同实现，如图1所示。

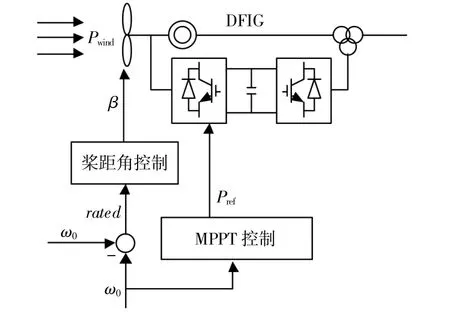
图1 DFIG功率控制Fig.1 Power control of DFIG

在额定风速以下，桨距角控制不动作，当风机稳态运行时，此时风机功率输出值Pref等于MPPT下最大有功功率。

为了让DFIG具有惯量响应特性以实现系统支撑作用，传统方法是在MPPT控制下的功率输出PMPPT添加一个功率偏差量 ΔPad，从而构 成DFIG新的功率输出参考值Pref。

ΔPad通过图1所示的DFIG功率控制中加入一个关于系统频率偏差的下垂控制回路，下垂增益为Kp，从而实现对Pref的调节，建立惯量控制环节。在传统惯量控制中，一般将风电场中各个风机的Kp设置为相同量，即对风电场中的任意风机i∈N，其功率偏差量为

式中:Δf为系统频率偏差量。

风电场在传统惯量控制下，所能提供的功率P为

式中:N为风电场中风机集合。

2 自适应最优惯量控制器设计

传统惯量控制中所有风机的Kp均相等，故每台风机所承担的功率减载量相同[9]，因而处于高风速条件下的前排风机，必须启动桨距角控制才能实现其有功功率的降低，因此造成了风电场对于风能捕获的损失。

实际上，在风电场惯量支撑过程中，相比前排风机，后排风机可以通过更大地提升转速幅度以降低其功率输出，将风能转化为旋转叶片中的动能并存储起来[10]，[11]。风机初始转速越低，则其转子转速的提升空间就越大，其有功降低的幅度就越大，参与惯量支撑的能力就越强。因此，首先建立风电场功率调节目标下风机转子转速的最优设定模型，进而基于最优转速值自适应地调节惯量控制中的Kp，实现风电场自适应最优惯量控制器设计。

2.1 风机最优转速设定

对于特定风电场，当系统发生过频事件时，风机在最优转速下，首先应当满足系统功率平衡支撑，同时尽量减小风机偏离最优运行点带来的风能捕获的损失，即将存储在风机叶片中的动能最大化。基于此，风机最优转速设定问题本质上是一个同时满足功率平衡约束和转速运行约束下转子动能的最大化问题。

①优化目标:对于任意风机i∈N，其转子的动能为

式中:J为风机i的转动惯量。

假定风电场中所有风机的型号相同，故转动惯 量 相 同。在 最 优 转 速 ωopt=（ω1opt，ω2opt，…，ωnopt）下，风电场中所有风机叶片存储的动能最大，即:

②功率平衡约束:对于任意风机i∈N，当面临的风速恒定时，根据式（8），其功率输出为最优转速的多项式函数，即:

风电场总功率输出为

当过频事件发生后，风电场总功率输出应与负荷需求平衡，即最优转速下功率满足平衡条件。

③转速约束:以DFIG为代表的变速风机，其转速可以在一定的范围内变化，从而调节其功率输出水平实现系统支撑。令 ωi0为风机i在过频事件发生前运行在MPPT下的初始转子转速，ωiupbound为风机i转子转速上限，一般取1.25 p.u.，则最优转速优化范围为

风机最优转速的设定问题可以建模为

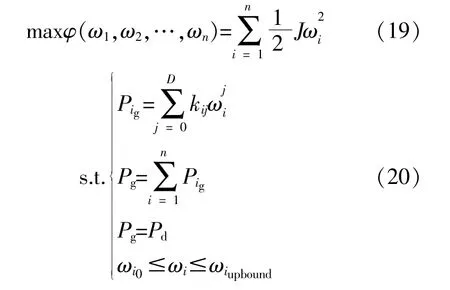
求解上述约束优化问题即可得到风电场内各风机在发生过频事件后的最优转速 ωiopt。如果过频事件中功率差额可以被风电场中所有风机分担，则不用启动桨距角控制。

2.2 自适应惯量控制器设计

根据分析可知，越后排的风机在惯量控制中具有更大的转速上升空间，故其惯量支撑作用就越大。对于第i∈N台风机，其下垂增益Kip的设计正比于风机最优转速 ωiopt与初始转速 ωi0的差值，以保证系统过频事件发生后，转子转速能提升至最 优 转 速 ωi_opt。

式中:Kb为基准下垂增益。

假定在最优转速条件下，风电场中所能提供的功率偏差总量可以抵消负荷功率的偏差量，即:

将 式（21）代 入 式（22）得:

联 立 式（21）～（23），可 得 惯 量 控 制 器 中 风 机i的Kip。

由 式（10），（11），风 机i的 功 率 偏 差 量 为

可知风机i的有功输出参考值为

显然，根据风机i的 ωiopt与Kip之间的对应关系，当Kip满足方程（21）时，风机转 子转 速 ωi为本节所提最优化模型的解 ωiopt。对于具有n台风机的风电场，其自适应最优惯量控制器的设计如图2所示。

图2 风电场自适应最优惯量控制器框图Fig.2 Adaptive optimal inertia control for wind farm

3 仿真实验及分析

为了对比本文方法与传统方法的差异，在MATLAB R2017b软件环境下，以图3所示的包括DFIG、负荷和传统同步机组成的5节点系统为例进行仿真，其中风电场中WT1，WT2，WT3和WT4分别为4台容量为2 MW的DFIG，其主要参数如表1所示。

图3 五节点仿真实验系统Fig.3 Five-bus simulation system

表1 风电场DFIG机组主要参数Table 1 Main parameters of DFIG

仿真系统利用一个容量为20 MW的7阶同步发电机模型SG代表主网，其参与一次调频的有功输出变化范围为其容量的4%，4台DFIG通过馈线连接到升压变压器，并通过PCC点升压后与同步发电机SG相联系，Pload是微网内总负荷。在本仿真实验中，仅考虑过频事件下PCC点断开后风电场的惯量控制仿真过程。

风电场中最前排风机WT1处于上风向位置，顺着风向在风电场中依次排列着WT2，WT3和WT4，最后排风机WT4处于下风向。根据尾流模型[9]设 置WT1，WT2，WT3和WT4面 临 的 风 速 分别 为14，13，12 m/s和11 m/s。在 过 频 事 件 发 生 前，所有风机均工作于MPPT点，因而WT1，WT2，WT3和WT4的初始转速分别为1.25，1.111 2，1.022 p.u.和0.936 9 p.u.，而风电场总有功功率为5.68 MW（0.71 p.u.）。当系统运行到第8秒时，由于部分负荷切除，为应对过频事件，PCC点与主网断开连接，由风电场中风机承担有功波动，因此风电场须要将有功功率降低为5.2 MW（0.65 p.u.），以保证系统的功率平衡。

3.1 风机转子转速实验

针对图3所示的仿真系统，在传统方案下，每台风机分担功率差额相同时，各风机转子转速如图4所示，而采用本文方案下，各风机转子转速如图5所示。

图4 传统方案各风机转子转速变化曲线Fig.4 Rotor speed of each turbine based on traditional scheme

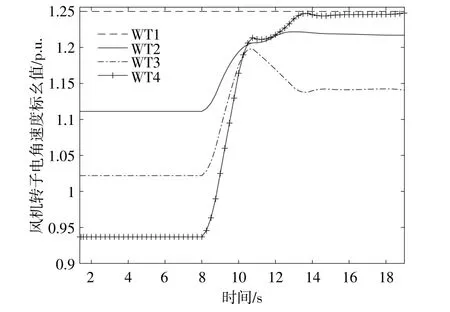
图5 本方案各风机转子转速变化曲线Fig.5 Rotor speed of each turbine based on proposed scheme

通过对比分析图4，5可知:在传统方案下，有功不平衡量由所有风机等额分担，由于WT1已经运行于额定最高转速，为了降低有功输出，只能启动桨距角控制，而WT2，WT3和WT4分别将其转速 提 升 到1.25，1.197 p.u.和1.096 3 p.u.，可 以 看 到后排风机WT3和WT4转速提升不明显 （表1），剩余的功率差额还需要开启桨距角控制才能实现。这种方案会带来一系列问题，比如响应速度慢、频繁激活桨距角会增加机械疲劳损伤，同时造成风能捕获量的降低，显然传统方案不是最优方案；在本文方案下，WT4转子转速提升最大，而随着所面临风速的升高，WT3和WT2转子转速提升幅度依次减少，WT1未承担降低功率输出的任务，转速仍保持在额定转速（图5），但是桨距角控制未激活。

3.2 风电场转子动能实验

在惯量支撑过程中，本文方案和传统方案风能捕获的不同如图6所示。

图6 风电场储存的动能Fig.6 Kinetic energy stored in wind farm

在传统方案下，通过功率差额均分，部分风机必须启动桨距角来消减其出力；而在本文方案下，功率差额并不是平均分担，而是根据最优转速设定值，实现自适应调整Kp。表2为恒定风速设置下的实验结果。前排风机WT1并不参与分担功率差额，其Kp为0，而其他风机因为未达到最高转速，通过最优转速设定大幅提升其转速，这样不但可以实现系统支撑，而且通过超速运行可以将更多的风能转化为转子动能。因此，在本文方案下，风电场中储存的风能有较大提升。

表2 实验数据Table 2 Experimental parameters

从表2可知，通过采用本文所提方案，风机转速的可提升幅度是不同的，通过合理设计Kp，在不启动桨距角控制系统的情况下，风机分担不同的功率差额。同时，本文方案在响应速度和风能有效利用方面具有明显的优越性。

3.3 变风速下风机转子转速分析

为了进一步比较本文方案的性能，在湍流风速下（图7），对比在过频事件下风电场内各风机转子转速的变化情况，结果如图8所示。

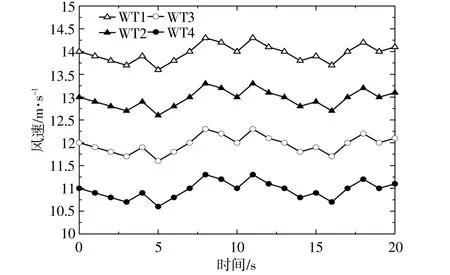
图7 风电场湍流风速Fig.7 Variable wind speeds in wind farm

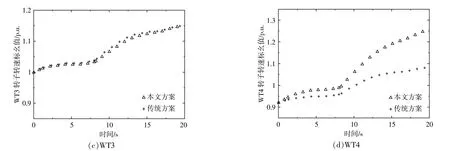
图8 风机转子转速Fig.8 Rotor speed of each wind turbine

湍流风速下仿真系统设置如下:在0～8 s时，系统正常运行，风机运行在MPPT模式，桨距角保持为0；当系统运行到第8秒时，由于部分负荷切除，系统过频事件发生；8～10 s为桨距角启动阶段，同时WT1转子转速持续增加以降低输出功率；10 s后WT1桨距角控制系统发挥作用，根据随机风速实时调整桨叶的角度，以承担功率消减任务来应对系统过频事件。

由 图8（b）～（d）中 转 子 转 速 变 化 可 知，对 于 后排风机WT2，WT3和WT4，由于其转子的初始转速处于较低水平，从而拥有较大的提速空间，可以通过大幅提升自身转速以承担更多的功率消减量，尤其是WT4，其惯量支撑能力最为突出。以WT1为例，在传统方案和本文方案下，WT1的桨距角变化情况如图9所示。

图9 WT1桨距角情况Fig.9 Pitch angle of WT1

4 结论

针对大规模风机并网造成的系统惯量支撑问题，本文设计了一种自适应最优惯量控制器。通过将风电场的惯量响应问题建模为风机转速优化问题，建立风机最优转速与下垂增益之间的关系，进而自适应设计惯量控制中最优下垂控制参数。仿真结果表明，本文方案在为系统提供惯量响应支撑的同时，最大限度地减少了风电场风能捕获能力的损失。