含分布式电源的主动配电网分层故障定位方法

2021-09-24李明阳张沈习程浩忠杨丹丹高勉伟倪识远

电力系统及其自动化学报 2021年8期

李明阳，张沈习，程浩忠，杨丹丹，高勉伟，倪识远

（1.上海电力大学电气工程学院，上海 200090；2.上海交通大学电子信息与电气工程学院，上海 200240；3.国网福建省电力有限公司宁德供电公司，宁德 352100；4.国网福建省电力有限公司经济技术研究院，福州 350003）

分布式电源DG（distributed generation）接入使传统的单电源辐射状配电网变为复杂的多电源配电网，由此造成故障电流的流向由单向流动变为双向流动[1-2]，同时DG投入与切除、故障电流信息发生畸变以及网络节点规模不断增加等问题对含DG的主动配电网故障定位提出了新的要求和挑战[3-5]。

主动配电网发生故障后，安装于各开关处的馈线终端单元FTU（feeder terminal unit）会检测到故障电流信息，并将其上传至监视控制与数据采集SCADA（supervisory control and data acquisition）系统[6-7]。现有研究已经提出了众多基于FTU 故障信息编码方式的故障定位方法。文献[8-9]采用矩阵算法进行配电网故障定位，考虑DG接入，动态构建信息矩阵，但是该算法求解变量维度大、计算复杂，在大规模配电网中定位速度较慢；文献[10]采用蚁群算法进行故障定位，当发生少量信息畸变时，具有较好的容错性，但对信息畸变问题的处理需要依赖于测量设备的精度，难以适用于配电网发生大规模信息畸变的情况；文献[11]结合区域划分思想，针对故障定位层级模型，采用二进制粒子群算法进行各层模型的求解进行求解，但没有针对各层模型的特点采用不同的算法分别求解，故障定位速度较慢；文献[12-13]采用遗传算法对配电网进行故障定位，提高了故障搜索能力，但是计算复杂度较高，定位速度较低，且容易陷入局部收敛；文献[14]在进行遗传操作时，通过动态地调整交叉、变异算子，收敛速度得到了提高，并且增强了算法的局部搜索能力，但是在遗传因子调整过程中仅考虑了种群在进化时的整体水平，忽略了个体间的差异性，变异与交叉因子的变化不够精确；文献[15-16]考虑DG 接入配电网引起的故障电流的多向性，对开关函数进行改进，但当DG投切情况发生改变时，需重新规定各开关所流过故障电流的正方向，在灵活多变的主动配电网中难以适用。

综上所述，目前针对含DG 接入的主动配电网故障定位研究主要存在以下问题：一是现有研究普遍采用单层故障定位模型，容错率和准确率较低，且定位速度较慢，随着大规模DG的接入，主动配电网节点规模逐渐增加，现有故障定位方法已难以满足故障定位快速性和准确性要求；二是智能算法普遍存在早熟收敛的问题，容易造成故障定位误判、漏判的情况发生。因此，研究新形势下具有快速性、高容错性的故障定位方法，对提高主动配电网安全稳定运行能力具有重要意义。

本文提出了含DG的主动配电网分层故障定位方法。首先，建立主动配电网故障信息编码方式以及开关函数；然后，通过分析故障位置对开关函数的影响，构建了基于端口定位以及区段定位的分层故障定位模型；针对该模型，提出了基于改进遗传算法GA（genetic algorithm）的端口定位方法以及整数线性规划ILP（integer linear programming）算法的区段定位方法。仿真结果表明，本文所提分层故障定位方法在发生大面积信息畸变的情况下，仍然可以实现准确定位，具有较高的容错性，并且与其他模型及算法相比，求解速度快，准确率高。

1 含分布式电源的主动配电网分层故障定位模型

1.1 故障信息编码方式与开关函数的构建

1.1.1 故障信息编码方式

主动配电网发生故障后，SCADA系统得到的是安装在节点开关的FTU 上传的开关故障电流信息[17]。本文用xi（i=1,2,…,D）表示第i条区段的故障状态信息，其中D为系统中所含区段总数，其编码方式为

用Sj表示开关j处FTU 上传的故障电流状态信息，其编码方式为

1.1.2 开关函数

要通过分析FTU 上传的开关故障电流信息实现故障定位，需要将其与区段故障信息建立起关系，开关函数就是起到此作用。

对于单电源的传统配电网，开关函数的表达式为

式（3）开关函数只适用于传统单电源辐射状配电网，对于含有DG的主动配电网而言，其网络结构复杂多变，上述开关函数已不再适用。因此，为了将区段状态和开关状态建立联系，本文定义网络关系系数用来描述开关与区段之间的拓扑关系，并规定开关j与主电源或其他分支线路开关之间的区段称为开关上游区段，其与本线路其他开关之间的区段称为开关下游区段，其网络关系系数表示为

同时，为了能够动态适应DG 的投切，引入DG投切系数kDGj来动态反映DG 的投切状态，建立了改进的开关函数为

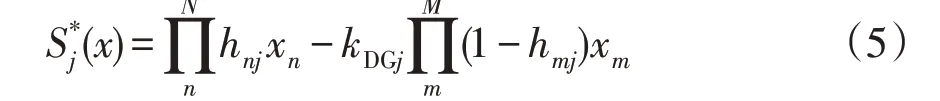
式中：xm为开关j上游区段m的状态信息，故障时为1，正常时为0；xn为开关j下游区段n的状态信息，故障时为1，正常时为0；kDGj为开关j的DG 投切系数，反映该开关所在分支是否接入DG，若接入DG 则为1，否则为0；M为开关j上游的馈线区段集合。

1.2 基于对外等效定则的网络简化分析

对于含有众多节点的主动配电网而言，单层定位模型一方面扩大了变量规模，求解耗时增加，难以满足故障定位实时性的要求；另一方面需要在每个节点开关处安装功率方向元件，这无疑会导致投资成本的增加。同时单层定位模型没有反馈修正环节，难以保证故障定位的准确性及容错性。

以含多分支的主动配电网为例，分析开关函数构建中的逻辑规律，含有5个分支的主动配电网拓扑如图1所示。

图1 主动配电网拓扑Fig.1 Topology of active distribution network

（1）当分支L5 上的区段（15）发生故障时，根据式（5）计算可得分支L1～L2上各开关的开关函数分别为

通过上述分析可知，故障区段所在分支上无论发生几处故障，对其他非故障分支中所有开关的开关函数影响均相同。因此，本文根据二端口网络对外等效定则，对图1所示的主动配电网各分支进行二端口等效，结果如图2所示。

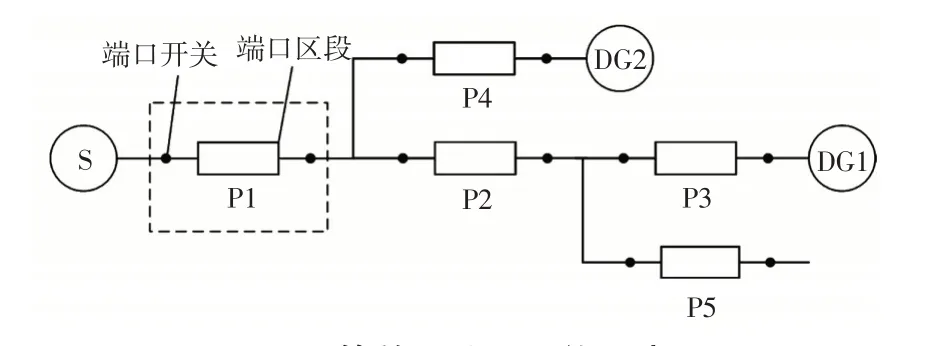
图2 等效二端口网络示意Fig.2 Schematic of equivalent two-port network

图2 中各端口内靠近主电源侧的开关定义为端口开关，端口内部所包含的区段为端口区段。最终，节点18 主动配电网等效为5 个二端口，变量维度较单层故障定位模型下降72.22%，这为构建分层故障定位模型提供了理论基础。

1.3 分层故障定位模型的建立

1.3.1 端口定位模型0，0]，目标函数为：f(x)=70-(0+1)=69。

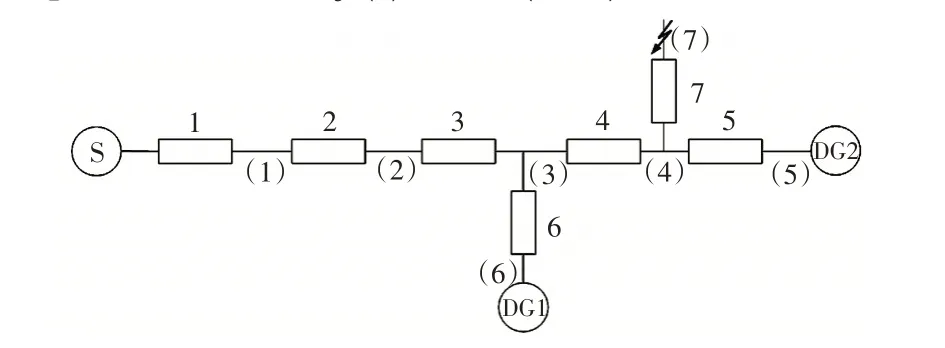
图3 含DG 的主动配电网Fig.3 Active distribution network with DGs

式中，D1为主动配电网等效二端口个数。

1.3.2 区段定位模型

区段定位是在故障端口内部展开的，配电网经二端口等效以后，其内部一般所含开关及区段相对较少。考虑到区段定位模型的变量即为故障端口内各区段的状态，均为0-1离散变量，并且ILP在解集较小时适用性更好，求解速度更快，但端口定位模型式（14）中存在绝对值，因此难以利用ILP进行求解。

本文引入辅助变量Aj(x)、Bj(x)，约束为

为了描述网络中各开关与区段间的上下游关系，引入网络描述矩阵H，表示为

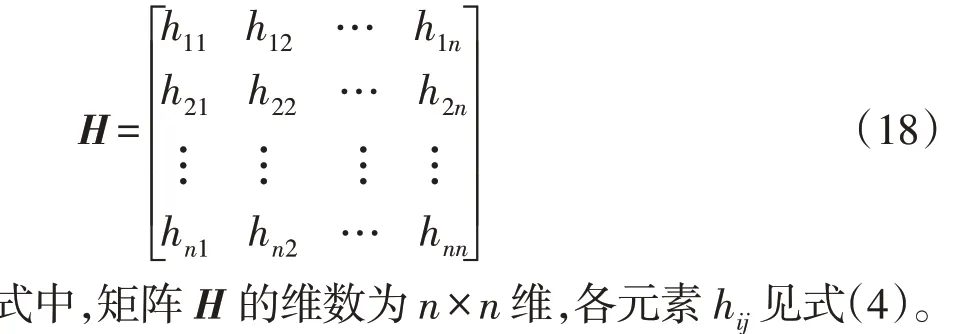
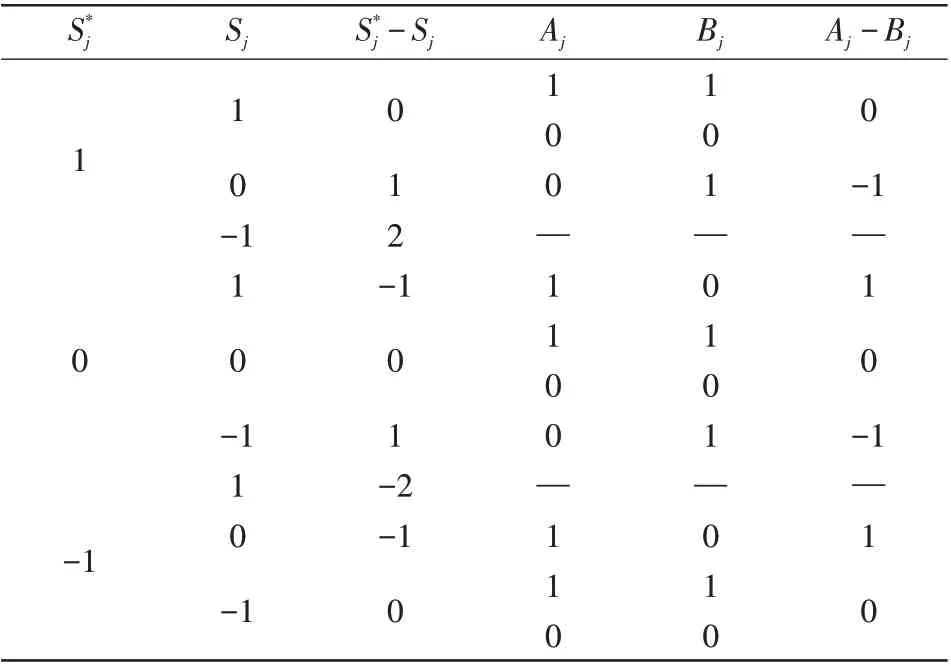
表1 开关函数、故障电流、辅助变量状态Tab.1 Status of switch function，fault current，and auxiliary variable

为了描述主动配电网中各开关所在线路的DG投切状态，引入DG投切矩阵KDG，即

式中，D2为故障端口内部所含区段数。可以看出，每次DG 投入或切除时，只需修改各开关所对应的DG 投切系数kDGi即可重新生成新的DG 投切矩阵KDG，从而能够动态适应DG的投切。

2 分层故障定位模型的求解策略

本文所建立的故障定位分层模型有含绝对值的端口定位模型和不含绝对值的区段定位模型。具体求解思路为：①针对端口定位模型，目标函数中因含有绝对值运算，变量维度较大，采用遗传算法进行求解将具有优势，故本文利用遗传算法对端口定位模型进行求解，来验证所建端口定位模型的正确性；②针对区段定位模型，输入变量为各故障端口内部的开关的故障电流状态信息，变量维度一般较小，采用ILP算法即可快速确定故障区段。

2.1 端口定位模型求解

在遗传算法中，变异决定着算法的局部搜索能力，交叉表示个体间基因是否进行重组，决定着算法的全局搜索能力，因此只有合理选择交叉概率和变异概率，才能提高遗传算法的寻优能力，保证良好的收敛性能[21]。

在传统遗传算法中，交叉概率和变异概率为一固定值，即每个个体具有相同的进化特性，可能会导致优良个体的基因被破坏，并且不利于遗传算法进行快速准确求解。针对传统遗传算法普遍存在早熟以及收敛速度慢的问题，本文引入评价系数用来反映每代种群不同个体间的进化特性，使种群在进化时，可以依据其进化特性动态地调整交叉概率及变异概率，提升搜索能力的同时能够避免算法陷入局部收敛。其中第i代个体j的评价系数u(i,j)为

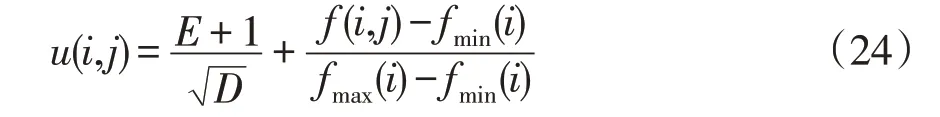
式中：E为期望值，反映种群适应度的平均水平；D为方差，反映个体间的偏离程度；f(i,j)为要进行变异、交叉的第i代个体j的适应度，fmax(i)和fmin(i)分别为第i代中个体适应度最大值与最小值。

式（24）考虑了各代个体之间的相似程度，可作为不同个体进化特性的评判依据，使个体在进化时能根据各自的评价系数动态地调整交叉概率以及变异概率，按照本身的进化特性以及与其他个体间的关系进化。在进化前期，种群内个体之间的差异比较大，相似程度较低，种群基因比较丰富，此时远离最优解，因此应给予较大的交叉概率和较小的变异概率，增加算法的全局搜索能力，以便更快地出现最优解；随着进化代数的增加，种群内适应度值较高的个体接近最优解时，种群基因多样性逐渐降低，个体间相似程度较大，种群趋于收敛。为了避免陷入局部收敛，应适当增大变异概率，同时为了避免优良基因被破坏，通过最优保持的选择手段保留上一代适应度前10%的个体。

Sigmoid 函数是一个在遗传进化过程中常见的S型函数，也称为S型增长曲线，能够较好地反映个体间的差异特征，其定义为

式中，各参数根据交叉、变异的概率范围进行取值，一般取pc∈[0.7,0.9] ，pm∈[0.05,0.1] ，则kc1=0.9 ，kc2=0.2，km1=0.05，km2=0.05。可见，随着评价系数u(i,j)的增加，个体交叉概率减小，变异概率增加。

由于传统GA 算法的交叉操作是随机的，在进化后期可能造成大量个体集中于一点，导致近亲繁殖，为此，本文将所有个体均标上X、Y染色体，将种群分为2种不同性别的子种群，在一定程度上避免了局部收敛情况的发生，提高了GA 搜索速度的同时保证了种群基因的多样性。

本文采用种群中出现适应度为(M-w)的个体或者迭代次数超出最大迭代次数时端口定位结束，其中最大迭代次数设置为60 代。最后将适应度最大的个体作为故障端口输出结果。

2.2 区段定位模型求解

根据所提分层故障定位模型的特点，第1 层端口定位模型通过二端口等效将原始网络化简后，利用改进GA 进行求解可确定故障端口，其内所含开关及区段即为第2层区段定位模型的输入变量，每个端口内部包含的开关数目一般较少，变量维数得到大幅降低，只需在故障端口内部进行寻优即可。考虑到ILP 适用于解空间较小的样本，具有全局寻优能力且求解速度快，因此本文采用ILP 对区段定位模型进行求解。

2.3 分层故障定位模型求解流程

首先，根据第1.2节所述的方法，将主动配电网中所含馈线支路分别等效为一个二端口，形成端口定位模型，各端口内部所含开关和区段为区段定位模型；然后，根据FTU上传至SCADA系统的故障电流信息，提取各端口开关对应的部分，采用改进GA对端口定位模型进行求解，确定故障端口；然后，读取故障端口内部所有开关的故障电流信息，并通过ILP 对区段定位模型进行求解，若端口定位结果与区段定位结果相一致，则输出该端口故障区段，否则判定为该端口开关发生畸变，端口无故障；接着对下一个故障端口内进行区段定位，当所有故障端口均完成区段定位时，定位结束，输出所有故障区段。具体分层故障定位流程如图4所示。

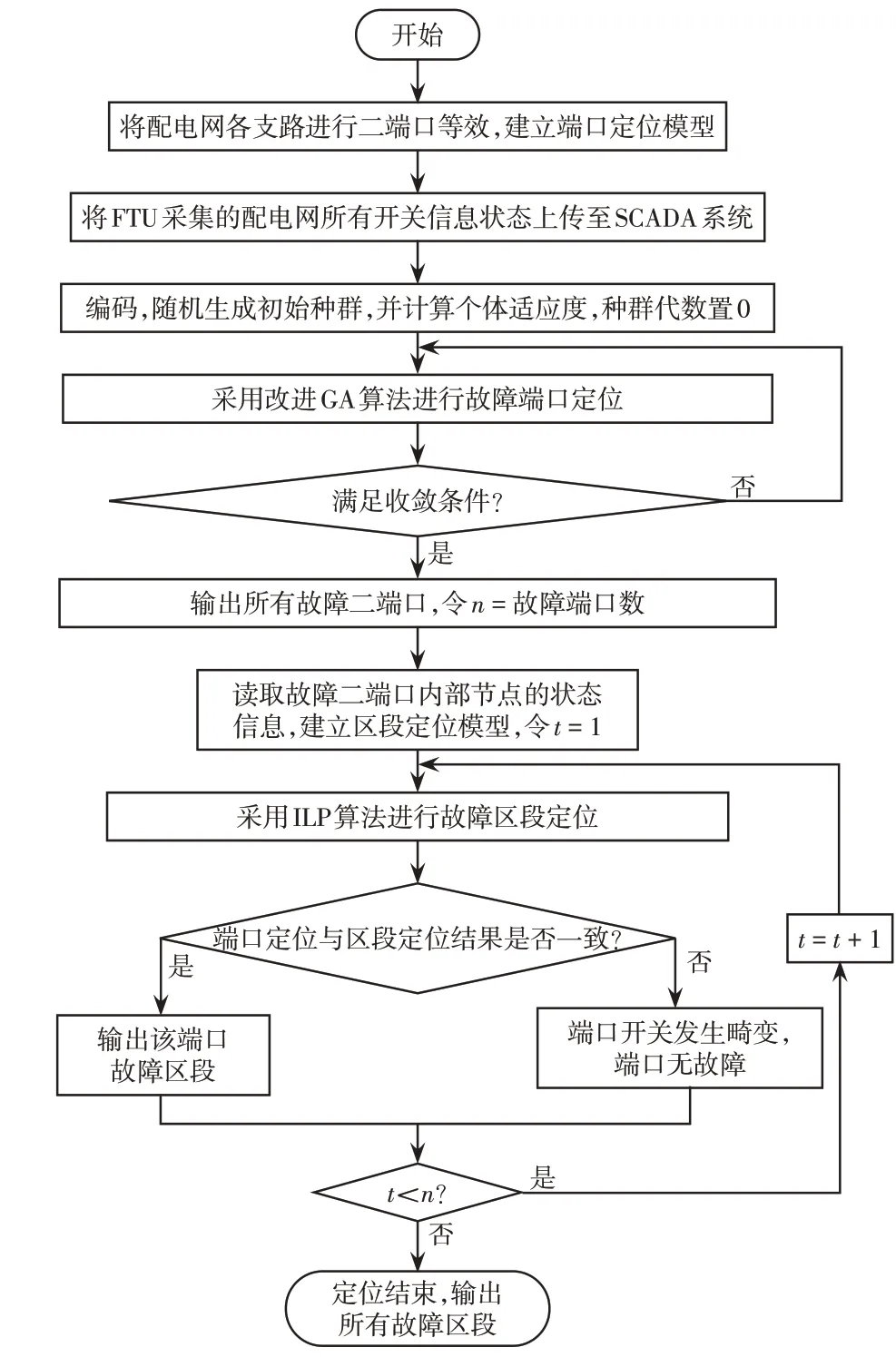
图4 分层故障定位流程Fig.4 Flow chart of hierarchical fault location

3 算例分析

针对所建立的主动配电网分层故障定位模型及其求解方法，在Matlab R2018a 环境下编写程序。计算机采用的系统配置为Intel（R）Core（TM）i7-8750H 处理器，CPU2.20GHz，内存8 GB，Win⁃dows10操作系统。

3.1 单故障与多故障分析

为验证本文所提分层故障定位模型及求解算法的有效性，以如图5所示含DG的改进IEEE 33节点主动配电网作为算例。其中，白色长方形为开关，编号1～33；两长方形之间为馈线区段，编号（1）～（33）。定义K为DG 投切矩阵，规定K=[k1，k2，k3，k4，k5]，其中各元素分别为DG1～DG5 所对应的DG投切系数。

图5 IEEE 33 节点主动配电网Fig.5 IEEE 33-node active distribution network

1）原始网络的二端口等效

首先，根据第1.2节所述方法，以馈线分支处靠近主电源的开关作为端口开关，将图5的主动配电网等效为端口P1～P10，如图6所示。各端口内包含的开关和区段如表2所示，表中首开关为端口开关。

图6 第1 层故障定位模型Fig.6 First-level fault location model

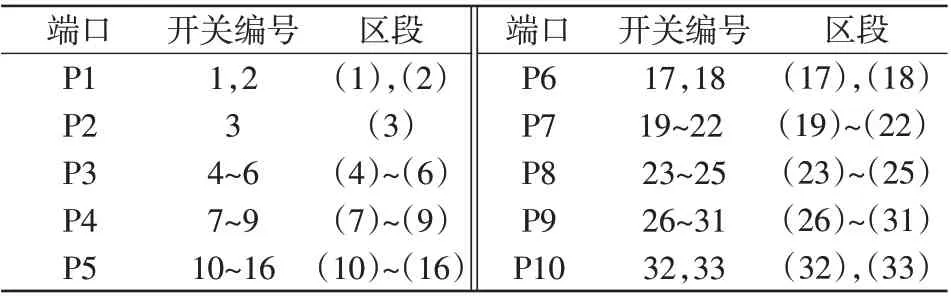
表2 二端口内包含的开关和区段Tab.2 Switches and segments included in two ports

2）故障仿真验证

对图6所示系统中端口P3的区段6设置故障，所有DG均投入运行。FTU上传的故障电流状态信息为[1，1，1，1，1，1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，0，0，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，0，0]，读取表2 中二端口包含的所有端口开关的故障电流信息[1，1，1，-1，-1，0，-1，-1，-1，0]，利用改进GA进行故障端口定位。

当改进GA 迭代至第10 代时，满足收敛条件，出现个体目标函数最大值为69.5，对应编码为[0，0，1，0，0，0，0，0，0，0]，判定端口P3 发生故障。读取P3内部包含的开关故障电流信息[1，1，1]，利用ILP进行区段定位，当出现个体的目标函数为69.5时定位结束，其编码为[0，0，1]，判定区段（6）发生故障。

考虑单一、多重故障，以及不同DG 的投切组合、FTU 上传数据畸变的情况，对故障定位进行仿真验证，其仿真结果如表3所示。

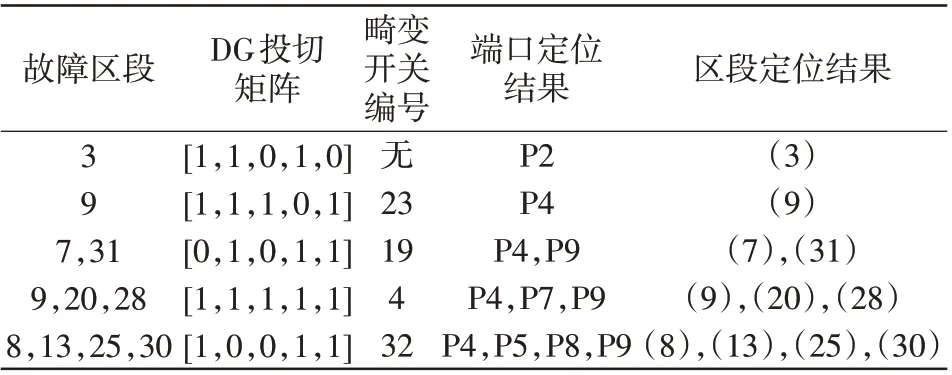
表3 单故障与多故障仿真结果Tab.3 Simulation results under single and multiple faults

以上仿真表明，无论是发生单故障还是多故障，将故障定位分层模型运用于含DG 的主动配电网中，变量维度较采用单层定位模型降低了69.7%，极大地简化了故障定位模型，最终故障端口、故障区段定位的结果也与预先设置的故障位置一致。综上所述，在含DG的主动配电网发生单一、多重故障时，所提分层故障定位方法均能够准确定位出故障区段，自适应性良好。

3.2 容错性分析

FTU开关通常选择安装在户外，并且运行环境较为恶劣，导致其上传故障电流信息畸变的情况时有发生。为验证本文所提模型及算法在故障信息发生畸变情况下故障定位的容错性，设置端口P5的区段10 和端口P10 的区段33 同时发生故障，端口P3内的开关4的和端口P8内的开关23处上传的故障电流信息发生畸变，分别从1变为-1和从-1变为1。首先采用改进GA对端口定位模型进行求解，所得结果为端口P3、P5、P8、P10 发生故障。随后，采集故障端口内开关的故障电流状态信息，采用ILP 对区段定位模型进行求解，区段故障定位结果如表4所示。

表4 区段故障定位结果Tab.4 Results of segment fault location

由表4 可知，由于端口定位模型中所采用的为各个端口开关的故障电流信息，因此端口P3、P8内的端口开关4 和23 信息发生畸变导致区段定位结果与端口P3、P8定位结果相矛盾，端口定位出现部分错误，此时应判定端口P3、P8无故障。而区段定位结果与端口P5、P10 定位结果相一致，即端口内存在故障，定位结果为区段（10）、（33）同时发生故障，输出故障区段。从上述分析可知，端口P3、P8内开关发生信息畸变，但通过区段定位与端口定位结果的一致性选择是否输出故障区段，能够准确实现故障定位，保证故障定位具有一定容错性的同时还可及时发现端口开关故障电流信息的畸变情况。

3.3 与其他模型及算法对比

为验证本文所提分层故障定位模型在容错性上的优越性，设置不同畸变开关规模，并将其与采用传统GA算法求解的单层模型、文献[11]中采用二进制粒子群优化BPSO（binary particle swarm opti⁃mization）算法求解的分层模型进行对比，定位结果如表5所示。

表5 容错性对比结果Tab.5 Comparison results of fault tolerance

结果表明，采用单层故障定位模型时，当开关畸变数量超过3 个，开始无法准确定位故障线路，而文献[11]与本文均采用分层故障定位模型，定位过程分两次进行，变量维数较低，受畸变影响较小，在开关畸变数量达到5个时，依然能够准确定位故障线路，但当畸变开关数量达到6个时，文献[11]所采用的方法定位出现错误，而本文所提方法仍然可以准确实现故障定位，这是由于本文采用的改进GA可以根据种群的进化特性自动调整个体的进化因子，从而有效避免陷入局部收敛，并且本文所提模型在进行求解时，能够根据所提分层定位模型的特点，采取改进GA 与ILP 的混合求解策略，保证了故障定位具有较强的容错性，能够良好地适应大规模开关故障电流信息发生畸变的情况。

为了验证本文所提的分层故障定位模型及求解算法在准确性及定位速度的优势，将其与采用传统GA 算法的单层模型、文献[11]中采用BPSO 算法的分层模型进行对比分析。设置区段（7）发生单故障和区段（7）、（21）、（16）、（31）发生多故障，并在两种故障情况下采用上述模型及算法分别运行100次，统计准确率及求解时间。图7 和图8 分别为单故障与多故障100次仿真耗时曲线运行结果。

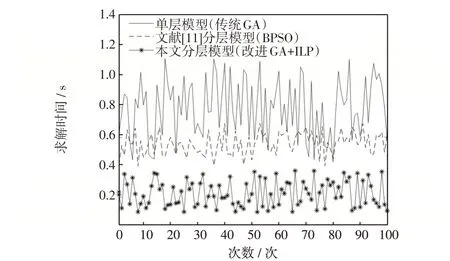
图7 单故障100 次仿真耗时曲线Fig.7 Curves of simulation time under single fault for 100 times

图8 多故障100 次仿真耗时曲线Fig.8 Curves of simulation time under multiple faults for 100 times

单故障对比结果和多故障对比结果分别如表6和表7所示。其结果表明，在单故障情况及多故障情况下，采用传统GA 求解的单层定位模型准确率仅有92%和89%，平均求解时间分别为0.794 6 s 和1.611 8 s。采用文献[11]中的分层模型并利用BPSO求解，在发生单故障时定位准确率为99%，发生多故障时，准确率稍有降低为97%。平均求解时间较采用单层定位模型在发生单故障及多故障情况下分别降低了29.85%和40.61%。但在单故障与多故障情况下的平均求解时间相差较为明显，说明该方法受故障点数量的影响较大。采用本文所提的分层模型并利用改进GA 与ILP 相结合的策略进行混合求解，在发生单故障及多故障时，定位准确率均可达到100%。平均求解时间分别为0.224 4 s 和0.246 8 s，较文献[11]中的方法在发生单故障及多故障时分别降低了59.75%和74.21%，并且在发生单故障及多故障情况下，平均求解时间相差不大，说明本文所提模型及求解方法可适用于发生大面积故障的情况。