计及需求侧响应的光伏微网群与主动配电网双层优化

2021-09-24吕智林廖庞思

电力系统及其自动化学报 2021年8期

吕智林，廖庞思，杨啸

（广西大学电气工程学院，南宁 530004）

太阳能、风能等可再生能源取之不尽用之不竭的特性将使其成为未来电力系统主要能源。而主动配电网ADN（active distribution network）的发展旨在提高配电网侧的可再生能源渗透率，优化能源结构[1]。多个微电网组成微网群，相互成为备用能量，互济富余电力也成为对可再生能源进行充分利用的有效方法之一。在电力市场环境下，微网与微网或微网与主动配电网相连才能获得更大利益[2]。

目前已有许多文献对微网并入主动配电网做了讨论和研究。文献[3]提出了一种并网多微网-主动配电网双层优化模型，利用上层ADN 系统的优化结果约束下层多微网MMG（multi-microgrid）从而得到MMG 的分布式电源DG（distributed genera⁃tion）规划；文献[4]采用目标级联法对ADN 系统和MMG 分别进行优化调度，通过将联络线功率作为解耦变量，实现微网自治模型与配网优化模型的解耦与并行求解；文献[5]提出了一种以上层配电系统作为领导者，下层微网作为追随者的非线性双层优化模型，解出上层最小化成本和下层MMG 的最大化利润；文献[6]提出一种多微网-主动配电网两层嵌套模型，以内层ADN 系统的调度结果作为外层微网调度模型的约束实现多微网的经济优化调度。

上述文献都是对微网和ADN 系统分别进行建模和优化，从而使双方达到经济效益的最大化，但在优化过程中没能考虑不同类型微网用户的用电特性。为了能更好地引导用户进行需求侧响应，本文结合了商业型、办公楼型和住宅型3种微网的用电特性，利用需求侧响应DR（demand-side response），引导用户改变用电习惯来节能降耗。需求侧响应是供需侧制定用电协议，由用户自发进行用电调整来参与供需功率平衡调节的方式。需求侧管理不仅能够提高分布式电源的渗透性，还能弥补DG 发电的间歇性[7]。文献[8]提出了一种基于多智能体系统的多步分层优化算法，将储能电池、需求侧响应和可控发电厂作为调节单元根据各微网的能量盈余和短缺信息实时进行调控；文献[9]结合冷热电可平移负荷的特性，建立了包含可平移负荷的综合能源运行成本的优化调度模型，最后算例表明了负荷平移具有削峰填谷，减少综合运行成本等方面的作用。在考虑能源效益方面，使用基于多智能体一致性的分布式能源管理方法能有效解决微网群中能源互联网的能源管理问题[10]，微网间将剩余能量进行互济调节能提高可再生能源消纳率，且每个子微网只需要与相邻微网进行少量的信息交换，与传统集中式调度方法相比，收敛速度更快，加快指令产生与下达，符合实时动态调度的需求[11]。

针对城镇区域光伏发电较普及而风力发电较少的情形，本文提出了考虑用户需求侧响应的光伏微网群-主动配电网双层优化调度模型，将下层光伏微网通过一定的拓扑结构组成微网群集系统，使用一致性算法将经济调度问题转换为功率分配过程中成本一致性问题，在保证微电网群整体实时功率平衡的同时能降低功率调节所耗费的成本。微网群通过联络线PCC（point of common coupling）与ADN进行买卖电交易，根据微网群的电能情况来决定其是当作虚拟负荷，还是当作虚拟电源来参与上层主动配电网最优潮流的优化调度，上层的配电网模型以系统网络损耗最小为目标函数，对最优潮流模型进行线性化出处理，解出满足潮流约束下的配电网层DG出力。

1 微网群-主动配电网协调优化调度策略

为提高微网的经济效益和环境效益以及能源效益，本文提出的策略主要考虑微网群并网运行时与ADN 系统交互的两种情况：有能量剩余向ADN系统售电，无法满足用电需求时先微网群内部互济调节再向ADN 系统购电，通过与ADN 交互减小分布式电源出力的不确定性和负荷波动性对微网群的影响；上层ADN 系统与下层微网群作为不同的利益主体分别建模优化，上下层优化调度既独立又互相关联，上下层之间以PCC功率作为解耦变量进行优化，分别求解出各自的决策变量与目标函数。

1.1 下层微网群功率调节策略

本文将多个光伏微网互联组成微网群，使得微网群里的各个子微网实现能源共享，在各自负荷高峰和低谷时段能进行能量互济。各子微网都含有光伏PV（photovoltaic）发电机、储能系统ESS（ener⁃gy storage system）、固定负荷FL（fixed load）以及需求侧的柔性负荷。柔性负荷包括可转移负荷TL（transferable load）和可中断负荷IL（interruptible load），其中，可转移负荷是指一类使用时间灵活的负荷，根据协议用户可在用电高峰时段的原本用电需求转移到用电低谷时段或可再生能源出力高峰时段使用；可中断负荷则是根据协议在用电高峰时段可直接中断使用的负荷。

本文研究的对象是光伏微网群与主动配电网，因此对微网群进行功率调节时从供给侧和需求侧两个方面来考虑，所以主要的调节方式包括：储能系统充放电、多微网间的协调、需求侧响应以及向ADN系统买卖电。

1.2 上层主动配电网优化调度策略

改进的IEEE-33 节点主动配电网系统结构如图1 所示。本文提出的微网群-主动配电网联合调度策略通过PCC 联络线将微网群接入配电网的14节点处，微网群优化得到的PCC功率会作为线路参数参与上层的经济调度。

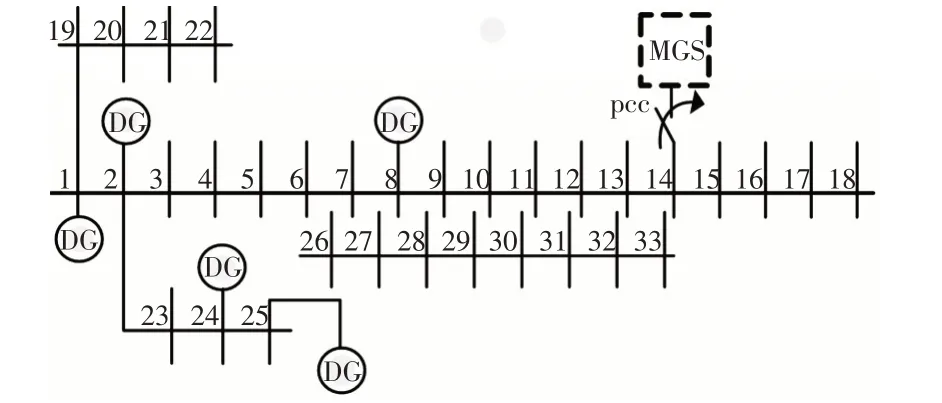
图1 接入微网群的主动配电网系统结构Fig.1 Structure of ADN system connected with MMG

2 微网群-主动配电网协调优化调度数学模型

2.1 微网群优化调度模型

微网群的优化调度以储能电池充放电、向外购电和需求侧响应3 种功率调节方式来实现功率平衡，平抑光伏出力和负荷的波动。以微网群经济成本最优的角度建立微网群优化调度模型，在满足各调节单元的功率约束条件下，实现微网群供电可靠性和经济性。

2.1.1 微网群优化目标

微网群的优化目标是实现微网群售电收益最高，调节成本最低，因此目标函数是售电收益与调节成本之和，表达式为

式中：Pb,t为t时段微网群向ADN购电或售电功率；ρ1为购电价格，购电情况下Pb(t)为负；ρ2为售电价格，售电情况下Pb(t)为正。

各调节单元的调节成本分别表述。需求侧响应的调节成本为式中：Ppv,i,t为微网i在t时段的光伏出力功率；Pb,t为t时段微网群与主动配电网交易功率，即PCC 联络线功率；PL,i,t为微网i在t时段的负荷需求；Pdr,i,t为微网i在t时段的需求侧响应功率，包括该时段从原本负荷需求功率中转移出去和中断使用的负荷功率。每个子微网在t时段的需求侧响应功率为上述两种类型的需求侧响应功率之和，即

式中：Ptr,i,t为微网i在t时段的转移负荷功率；Pir,i,t为微网i在t时段中断的负荷功率。需求侧响应调节中进行负荷转移的优先级比中断负荷高，即若需要进行需求侧响应的时段正好在转出负荷的时间约束内则优先考虑转出负荷。

（2）储能系统功率约束为

式中：Ptr,i,max为微网i的最大转移负荷功率；Pir,i,max为微网i的最大可中断负荷功率。微网i在t时段的转移状态变量di,t和转移负荷功率Ptr,i,t分别为

（5）联络线功率约束为

式中，Ppcc,min和Ppcc,max分别为PCC 联络线功率的最小值和最大值。

下层优化得出的微网向配电网购电或售电功率Pb即为联络线功率。

2.2 上层配电网系统最优潮流模型

2.2.1 目标函数

最优潮流模型以ADN 系统网络损耗最低为目标，求出网损最低情况下的发电成本。目标函数为

式中：C(PGi)为发电机组运行成本；PGi为第i个发电机组的有功发电功率；N为发电机组个数；αi、βi、γi分别为第i个发电机的耗量特性曲线参数。

2.2.2 约束条件

（1）功率平衡约束为

（2）功率上、下限约束和电压上、下限约束为

式中：Vi_min、Vi_max分别为节点i电压幅值的上、下限；PGimax、PGimin分别为发电机组i有功出力的上、下限；QGimax、QGimin分别为发电机组i无功出力的上、下限。

（3）二阶锥约束为

3 双层优化调度模型的求解

3.1 微网群优化模型的求解

下层微网群优化调度模型使用离散一阶一致性算法进行求解，该算法选取子微网的调节成本作为一致性变量。基于一致性算法的功率调节策略不需要中央控制器，当微网群功率不平衡时，子微网间只需要交换自身实时更新的一致性变量，达成一致后再各自逐级反解出决策变量。

由于迭代收敛得到的一致性变量即各微网的调节成本是一定的，所以已知调节成本可以根据调度优先级先后反解出分配到各调节单元的功率。在该功率调节策略中，储能单元输出功率、需求侧响应功率以及向ADN 购电功率3 个决策变量由一致性变量逐级反解得到，具体表现为调节成本低的单元优先启动。一致性算法求解过程中，若某个调节单元分配到的功率超出约束条件的限制，则取最大值为调节功率，若取该调节单元的最大调节功率仍不能满足功率平衡则启动下一个调节成本较低的调节单元进行调节，直到总调节功率能够填补微网群总体功率不平衡量且调节成本达到一致收敛。

单个微网的调节成本包括蓄电池充放电折旧成本Cdr,i、需求侧响应成本Ces,i和购电成本Cb,i，即

式中，Ci为第i个微网的总调节成本。

由文献[13-14]的一致性算法图论基础，3 个微网由环形结构的通信拓扑结构进行通信得出通信迭代矩阵为H，则微网的一致性变量更新公式为

式中，θ为收敛误差，本文取0.000 1。

综上，微网群的优化调度求解算法流程如图2所示。

图2 微网群功率调节流程Fig.2 Flow chart of MMG power regulation

在判断各微网出力是否满足负荷时，已经能实现自给自足的子微网独立运行，退出通信拓扑。当微网群中的子微网有电能剩余时，优先考虑把电能传输给电能不足的子微网，再考虑自身的储能进行充电。为避免弃光造成能源的浪费，售电功率取各子微网进行电能互济及ESS充电后剩余电量出售给配电网，微网群售电过程不需要进行一致性功率调节。

3.2 主动配电网优化模型的求解算法

上层的配电网模型以网络损耗为目标函数，将下层优化得出PCC 联络线功率代入上层最优潮流模型中求解出满足潮流约束下的配电网层DG 出力。式（17）导致了上层模型的非凸非线性，因此在模型求解之前用二阶锥技术通过重新定义变量将式（17）转化为式（19），再用Gurobi 求解器进行求解。模型求解步骤如下。

步骤1 将下层优化得到的PCC功率代入主动配电网线路参数中，开始读取数据。

步骤2 用二阶锥技术转化上层优化模型。

步骤3 调用Gurobi求解器解上层优化模型并输出DG出力与目标函数。

4 算例分析

4.1 算例参数

4.1.1 微网群基本参数

本文将微电网群视为能够直接实现能量互济的互联系统，不考虑微网间具体的接线方式。各微网所含设备与设备容量如表1所示。

表1 微网群的设备容量及数量Tab.1 Equipment capacity and quantity of MMG

假设蓄电池的初始荷电状态为10%，在光伏发电高峰期进行充电，在负荷需求峰值时段进行放电，对负荷曲线起到削峰填谷作用，充放电效率为90%，充放电折旧系数为0.05 元/kW。假设光伏消纳率为100%。一个调度周期为24 h，微网群的24 h光伏预测出力如图3所示。

图3 微网群光伏出力及负荷预测Fig.3 Photovoltaic output and load forecasting of MMG

图3 中负荷表示每个微网的总负荷，包括固定负荷、可中断负荷和可转移负荷，MG1 是商场区域微网，总负荷需求较高且高峰期在下午到晚上；MG2 是办公楼型微网，负荷用电高峰期在白天；MG3 是住宅区微网，高峰期为08：00 和20：00。为提高用户进行需求侧响应的积极性，根据可进行需求侧响应的负荷量并结合各时段用户响应的实际意愿为3个不同类型MG设定相应的补偿价格，3个微网支付给用户的需求侧响应补偿价格r1、r2、r3如图4所示。本文微网群与主动配电网的交易电价采用尖峰电价[15]，一个调度周期各时段电价如表2所示。

图4 微网群需求侧响应补偿价格Fig.4 Demand-side response compensation price of MMG

表2 微网群与ADN 交易的电价Tab.2 Electricity price for transaction between MMG and ADN

4.1.2 ADN 系统基本参数

ADN系统结构如图2所示，发电机组基本参数如表3所示。

表3 ADN 系统中各机组的特性参数与出力范围Tab.3 Characteristic parameters and output range of each unit in ADN system

4.2 结果与分析

4.2.1 微网群优化调度结果

对微网群进行24 h 调度，得到3 个微网的需求侧响应功率、与ADN 交易的电能功率以及储能充放电功率，结果分别如图5～图7所示。

图5 微网群需求侧响应功率Fig.5 Demand-side response power of MMG

图6 微网群买卖电功率Fig.6 Purchase and selling electric power by MMG

图7 储能充放电功率Fig.7 Charging and discharging power of energy storage

结合图3～图7，由于07：00—17：00 光伏出力充足，不需要向ADN 购电及启动需求侧响应进行调节，需求侧响应功率为0。在时段00：00—06：00和17：00—24：00 则需充分利用储能、需求侧响应以及向外购电来满足微网电能需求。图6 中数值为负表示购电，为正表示售电。MG1储能和需求侧响应调节单元的调节能力较强，需要承担更多的调节功率。但当3 个微网总调节成本达成一致时，MG2 和MG3 由于进行需求侧响应功率较小，所以需要帮MG1承担购电量，所以从图6可以看出MG2和MG3的购电量较大。3个MG在一个调度周期内的储能充放电情况如图7 所示，数值为正表示充电，为负表示放电。

图8 为3 个微网分别在一个调度周期内的收益，即功率调节成本与卖电收益的总和。在01：00—05：00、19：00—24：00 时段中3 个微网使用一致性算法进行功率调节，调节成本达成一致，所以3 个微网的调节成本相同。

图8 微网群收益Fig.8 Revenue of MMG

商业型MG1和住宅型微网MG3需求侧响应类型包含可转移负荷和可中断负荷，而办公楼型微网MG2只包含可中断负荷。实施DR调度后转移的负荷、中断负荷与原始负荷占比如图9～图11所示。

图9 MG1 实施DR 后的负荷功率Fig.9 Load power after DR of MG1

图10 MG2 实施DR 后的负荷功率Fig.10 Load power after DR of MG2

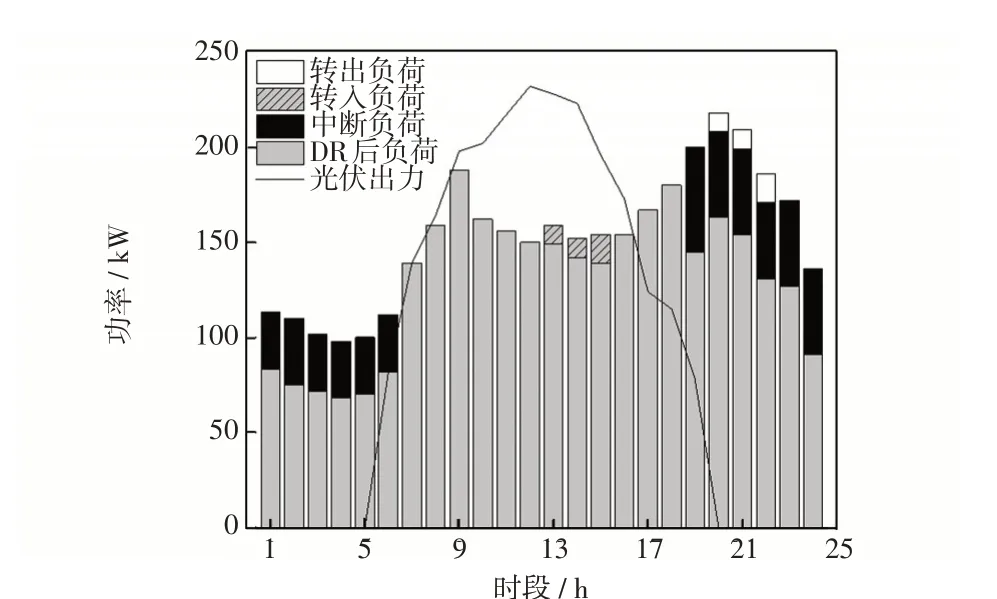
图11 MG3 实施DR 后的负荷功率Fig.11 Load power after DR of MG3

图9～图11 中的“DR 后负荷”表示进行需求侧响应后的总负荷（包括固定负荷和无需中断或转移负荷）。白色部分表示转移出去的负荷，阴影部分表示实施DR后转入使用的负荷。对比光伏出力曲线可知白天的光伏发电充足可以满足用户用电需求，不需要进行需求侧响应。进行负荷转移能起到一定的削峰填谷作用，协调进行两种需求侧响应能使调度周期内的负荷尽量趋近光伏发电输出功率曲线。

为验证下层基于一致性算法的功率调节策略的有效性，本文采用微网分散自治模式进行对比分析。模式1 中3 个微网互联成微网群，根据本文提出的功率调节策略进行调度。模式2中3个微网不互联，各自进行功率调节。2 种运行方式一个调度周期内功率调节费用如表4所示。

表4 2 种模式下微网功率调节费用Tab.4 Power regulation cost in two modes of microgrid

由表4可知：模式1中，微网群的调节费用比较平均地由3个微网承担，因为在此模式下微网间互通信息，总体功率不平衡时先由调节费用最低的储能单元放电，再根据各子微网进行DR 和向外购电调节费用高低进行调节功率的分配；模式2中，MG1的调节费用比MG2高出很多是因为MG1供需功率不平衡量较大，所以需要更多的DR 功率和向外购电来调节，产生的费用最多。然而使用模式1后能充分利用其他微网可调资源，把自身的调节压力分给另外两个调节成本较低的微网，实现微网群的能量互济且在使微网群实现功率平衡的前提下调节成本最小，获得更好的经济效益。

4.2.2 ADN 层联合优化调度结果

主动配电网24 h 调度的分布式电源出力如图12所示。

图12 主动配电网DG 出力Fig.12 DG output from ADN

图12中01：00—06：00和17：00—24：00时PCC功率为负说明微网群作为虚拟负荷连接到ADN 系统中。由于DG8 和DG24 机组参数较小，因此DG8和DG24 承担较大的出力变化，由图12 也可以看出，其他DG的出力变化较小。

ADN 系统的网络损耗如图13 所示，由图13 可知06：00—17：00时段的ADN系统网络损耗有所降低，因为该时段微网群向ADN系统售电，在ADN系统充当发电单元的角色，ADN的其他机组就可以减少发电，使得网损降低。

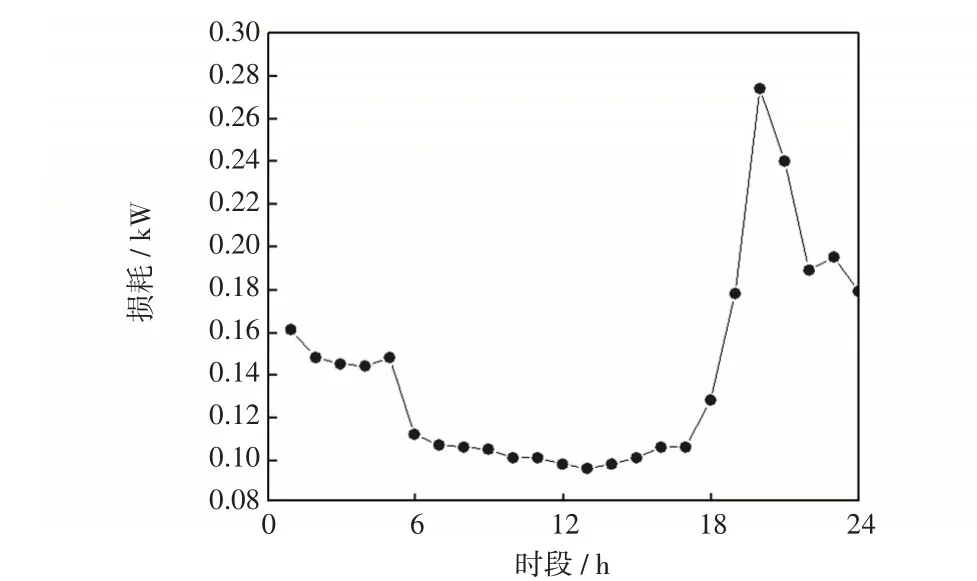
图13 主动配电网网络损耗Fig.13 Network loss of ADN

算例中把下层优化得到的PCC 功率代到上层最优潮流优化时，若在微网群可再生能源出力高峰时段不与主动配电网进行交易，弃风弃光的能量为629 kW，对自然资源造成很大的浪费。同时若在负荷高峰时段仅使用向外购电方式进行功率调节会使调节成本增多，所以采用本文提出的微网群-主动配电网联合调度方案能在保证用电可靠性的前提下提高经济效益和环境效益。

ADN 系统发电成本如图14 所示。由图14 可知，微网群向ADN售电时段，PCC联络线在ADN系统中当做电源供电，其他DG就可以减少出力，减小ADN系统的发电成本。