基于多尺度超像素的高光谱图像分类研究
2021-09-24李卫卫李志刚陈学业
王 华,李卫卫,李志刚,陈学业,孙 乐
(1.自然资源部城市土地资源监测与仿真重点试验室,深圳 518034;2.郑州轻工业大学河南省食品安全数据智能重点实验室,郑州 450002;3.南京信息工程大学计算机与软件学院,南京 210044)
0 引言
遥感影像由于其较高的时效性,一直被用作土地利用分类、医学图像处理、目标检测识别等信息采集、更新的主要数据源。高光谱遥感影像不仅包含地物空间信息,还包含丰富的地物光谱信息,在高光谱图像分类研究中,特征提取、数据处理、算法运用等因素会影响最终分类精度。因此,全面考虑图像特征信息、灵活运用算法对于提升高光谱图像分类精度具有非常重要的意义[1]。
目前,用于高光谱图像(hyperspectral image,HSI)分类的算法包括决策树[2-3]、支持向量机(support vector machines,SVM)[4-5]、深度学习[6-7]等,相比于一般遥感影像,HSI数据提供了更加庞大的细微光谱特征[8-10],使得传统的逐像素方法极易受噪声影响,并且在提取图像特征时往往忽略相似特征聚类的重要性,降低了分类精度[11]。超像素分割能够将图像中空间位置相邻且色彩、亮度、纹理等特征相似的像素点划分成小区域,能够将像素级影像抽象为区域级的高维数据[12-15],是应用较为广泛的图像分割方法[16-18]。将超像素分割方法运用到HSI分类或目标检测,可以提取更加有效的样本空间特征,进而提升分类效果或目标检测效率,如陈允杰等[19]基于超像素方法提升HSI的分类精度;刘忠林等[20]基于超像素图像模型,极大地提高了复杂背景下的小目标检测准确率。上述方法表明,基于超像素的改进方法可有效提高目标分类精度,但是将超像素分割应用到HSI分类中仍然存在以下缺陷:①将图像在单一尺度下进行超像素分割,无法精确判断初始超像素个数,数值过小可能会丢失关键判别信息,初始数值过大会包含过多干扰信息;②单一尺度的特征提取与单一核的特征分类很难提取较为精细的图像信息。较为合理的方法应在满足减少干扰信息的情况下,尽可能提取更加全面的判别信息。
基于上述研究,为有效提高HSI分类精度,本文提出一种耦合多尺度超像素分割与合成核(multi-scale spatial spectrum synthesis kernel,Ms-SSSK)的分类方法。该方法将HSI的第一主成分分量,在多个尺度下进行超像素分割,并融合所有尺度下的分割图像,以提取较为全面的图像空间光谱特征核矩阵,并通过权重与原始光谱核矩阵结合,形成多尺度空间光谱合成核矩阵,完成分类模型的构建与预测。本研究以Washington DC Mall HYDICE为实验数据,在MATLAB平台上对本文所提方法进行实现与测试,并将本文方法所得高光谱影像分类结果与多尺度滤波空间光谱核(multi-scale filtering spatial spectrum kernel,Ms-FSSK)、单一尺度下空间光谱合成核(single-scale spatial spectrum synthesis kernel,Ss-SSSK)方法、原始空间光谱合成核(original spatial spectrum synthesis kernel,O-SSSK)方法进行对比,验证改进方法的有效性及可行性。
1 研究方法
1.1 方法流程
Ms-SSSK方法将多尺度超像素和空间光谱特征结合,有效地提升了HSI的分类精度,方法总体研究流程如图1所示。

图1 模型流程图Fig.1 Overall flowchart
由图1可知,该方法提取了空间光谱特征和原始光谱特征2种分类特征,其中空间光谱特征获取步骤如下:①采用主成分分析(principal component analysis,PCA)算法对HSI降维,提取HSI的第一主成分分量;②在多个尺度下将提取的主成分分量采用基于熵率的超像素分割算法(entropy rate superpixel,ERS)进行超像素分割处理;③通过径向基核函数(radial basis function,RBF)计算每一尺度下的空间光谱核矩阵;④将所有尺度下的核矩阵做均值运算,得到空间光谱核矩阵。原始光谱特征获取步骤如下:①计算原始HSI中各像素所有波段的光谱均值;②使用RBF核函数计算各像素间的相似性,形成原始光谱核矩阵。随后,通过权值将空间光谱核矩阵和原始光谱核矩阵结合形成多尺度超像素空间光谱合成核,并随机选取训练样本和测试样本,索引出训练核矩阵与测试核矩阵,随后通过LIBSVM软件包进行分类模型的构建与预测。
1.2 数据降维
本文使用的HSI具有191个波段,每个像素点均包含大量的光谱信息,此外,相邻的波段之间具有紧密的空间、光谱关系,若使用全部波段的光谱信息进行影像空间光谱核形成的实验,将会因数据维数大导致实验时间的延长、实验工作的繁重。因此,为了快速、高效地完成空间光谱核形成工作,需要对HSI进行降维,目的是在众多波段中挑选出包含HSI大部分光谱信息的主成分分量,再使用该主成分分量进行实验,能够极大地提升分类效率。
一般情况下,用于数据降维的算法有线性判别分析(linear discriminant analysis,LDA)、PCA、局部线性嵌入(locally linear embedding,LLE)等,其中应用较为广泛的降维方法[21]是PCA,此方法降维步骤如下:①输入原始HSI数据a×b×n,将原始矩阵处理成m×n(m=a×b)的二维矩阵;②求出m×n矩阵的均值(μ)与协方差矩阵(C)n×n,计算C的特征值(λ)与特征向量(E);③将特征值从大到小依次排列,特征值越大则代表此特征越重要,若只提取前p个特征,则选取E中前p个列向量构造模式矩阵Ep;④将原始图像去中心化后形成矩阵A,最后通过计算[EpT×AT]T形成降维后的矩阵。本研究通过调用MATLAB软件中的PCA函数进行数据降维获得第一个主成分分量且贡献率为81.7%。
1.3 超像素分割
采用PCA算法提取高光谱影像的第一主成分分量之后,需要对第一主成分分量进行超像素分割处理,以确保具有相同或相似光谱特征的相邻像素同属一个类别标签,除此之外,图像进行超像素分割后,按超像素区域块执行运算操作,避免了逐像素运算的繁琐过程。
目前,用于超像素分割的常用算法有ERS、基于梯度下降法的超像素分割算法(simple linear iterative clustering,SLIC)、基于图论的超像素分割算法(Graph-based)等,本文基于ERS[22]对提取的主成分分量进行多尺度超像素分割处理。该方法通过定义目标函数计算每个像素顶点与其邻像素间边的函数值,函数值越大代表2个像素相似性越高、属于同一类别的可能性越大,将函数值最大的边删除,使2个像素同属一个超像素,依次计算所有像素顶点直至超像素个数等于设定超像素数值。通过ERS算法分割图像能够最大程度地保留图像边缘信息生成较优的超像素图像,并且在多个尺度下对图像分别进行超像素分割处理,能够使某一尺度中较难获取到的特性在某个尺度中轻松提取。每个尺度的数值需满足M=2L-1[23],其中L为尺度个数,超像素数量N=M×q,q为初始超像素个数,根据现有研究[24],本文选择4个尺度进行图像分割处理,并且q设置为400,各个尺度下的超像素分割图像如图2所示。

(a)N=400 (b)N=800 (c)N=1600 (d)N=3200
1.4 SVM
SVM是较为常用且能有效解决分类问题的机器学习算法,针对维度较高、样本较少等问题表现出良好的分类效果,最常见的是线性分类问题,对待线性不可分问题,需要通过核函数完成低维空间至高维空间的映射,随后进行分类研究[25],核函数定义为:
K(x,y)=<φ(x),φ(y)>,
(1)
式中:φ为映射;x,y为空间内任意点。常用的核函数有sigmoid核函数、高斯(RBF)核函数与线性核函数等,针对大、小样本,RBF核函数能够产生很好的性能,且涉及参数相对较少[26],因此本文选择RBF核函数进行研究,其表达式为:
K(Xi,Xj)=exp (-||Xi-Xj||/2δ2),
(2)
式中:δ是宽度参数,该数值的选取对分类精度会产生较大的影响;Xi,Xj为空间内任意点。基于2个有效核K1,K2,一个新的有效核可由下式产生,即
K(Xi,Xj)=K1(Xi,Xj)+K2(Xi,Xj),
(3)
K(Xi,Xj)=K1(Xi,Xj)·K2(Xi,Xj),
(4)
K(Xi,Xj)=μK1(Xi,Xj);μ>0,
(5)
式中μ为权重值。新构造的核函数K(Xi,Xj)由K1和K2进行组合,并且K1和K2可以应用于不同来源、时相的高光谱遥感影像数据[27-28],本研究通过式(3)将不同尺度下的空间光谱特征进行结合形成新的空间光谱核,通过式(5)以赋予权重值的形式将空间光谱核与原始光谱核结合形成合成核进行分类。
1.5 Ms-SSSK分类
本研究使用的高光谱数据集经过PCA提取主成分分量之后,在多个尺度下进行超像素分割处理,并将超像素特征定义为超像素中所有像素的光谱特征均值,通过RBF核函数计算每2个超像素的线性内积代表超像素之间的相似性,使样本映射至核空间形成核矩阵。实验中某一像素Xi1,其所在超像素Si={Xi1,Xi2,Xi3…Xik},超像素中像素集合的光谱均值为:

(6)

<Φ(Si),Φ(Sj)>=K(Si,Sj)=K(Simean,Sjmean),
(7)
由式(7)计算得出空间光谱核矩阵,遍历训练集中各个像素所在超像素位置并提取训练核矩阵,p个训练样本的训练核矩阵为p×p,随后在核空间中查找出测试样本中每个像素所在超像素位置,并找出与所有训练样本所在超像素间的相似性构成测试核矩阵。图像的尺度不同获得的核矩阵不同,将所有尺度下的核矩阵结合,公式为:
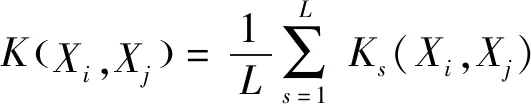
(8)
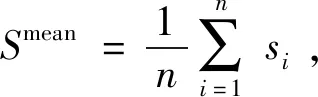
空间光谱信息的提取有利于建立各像元间空间关系,原始光谱信息的提取则更加注重地物间光谱差异有利于区分不同物体。提取出训练集与测试集的原始光谱核矩阵,并分别将训练集与测试集的空间光谱核矩阵与原始光谱核矩阵结合,公式为:
K=ϑKpp+(1-ϑ)Kyp,
(9)
式中:ϑ为平衡参数,范围为[0,1];Kpp为空间光谱核矩阵;Kyp为原始光谱核矩阵。用于构建分类模型的多尺度超像素空间光谱合成核矩阵的计算公式为:

(10)
式中si和sj分别为像素i和j的光谱信息。由式(10)计算得出训练核矩阵与测试核矩阵,并应用LIBSVM软件包进行分类模型的构建与测试样本集分类结果的预测,以验证本文方法分类性能,并通过分类模型得出整个区域内样本的所属类别,由此观察此区域地物分类现状。
1.6 实验方案
本文实验在原有Ms-SSSK方法的基础之上,设置了3组对照实验,分别为Ms-FSSK,Ss-SSSK和O-SSSK,每组实验的计算方法如下:
1)Ms-FSSK方法。Ms-FSSK由多尺度滤波和空间光谱核共同组成,其中多尺度滤波空间光谱核获得方式如图3所示。

图3 多尺度滤波空间光谱核获取流程Fig.3 Multi-scale filtering spatial spectrum kernel acquisition process
该方法中不同大小的滤波窗代表不同的尺度,将所有尺度下的空间光谱核结合求均值,得到多尺度空间多谱核,并通过RBF核函数获得原始光谱核,多尺度滤波空间光谱核与原始光谱核通过权值结合形成Ms-FSSK。
2)Ss-SSSK方法。Ss-SSSK由单尺度超像素空间光谱核与原始光谱核共同组成,其中单尺度超像素空间光谱核获得方式如图4所示。

图4 单尺度超像素空间光谱核获取流程Fig.4 Single-scale superpixel spatial spectrum nuclear acquisition process
获取原始高光谱影像各个像素所有波段的光谱均值信息,并通过RBF核函数得到原始光谱核矩阵,单尺度超像素空间光谱核矩阵与原始光谱核矩阵通过权值结合形成Ss-SSSK进行高光谱影像分类。
3)O-SSSK方法。O-SSSK由原始空间光谱核与原始光谱核共同组成,其中原始空间光谱核的获得方式如图5所示。

图5 原始空间光谱核获取流程Fig.5 Original space spectrum nuclear acquisition process
获取高光谱影像的第一主成分分量,随后使用5×5的窗口对主成分图像进行光谱均值提取,并使用RBF核函数获取原始空间光谱核矩阵,将原始空间光谱核矩阵与原始光谱核矩阵通过权值结合形成O-SSSK进行高光谱影像分类。
2 实验结果与分析
2.1 实验数据
本文实验使用的高光谱数据集为Washington DC Mall,去除不透明波段之后,此影像剩余波段个数为191。影像像素大小为1 280×307×191,本研究使用图像为591行以下部分数据(690×307×191)作为研究对象,并根据地面实际情况将研究区分为住宅、公路、街道、草地、林地、水域和阴影7种类别,各波段包含像素个数为211 830,其中样本集个数为5 471,7个类别的训练集和测试集个数如下表1所示。

表1 样本类别与样本集个数Tab.1 Number of sample categories and sample sets (个)
2.2 Ms-SSSK模型结果分析
本文选取具有191个有效光谱波段的HSI为分析对象,并将样本集中的5 471个已知地物类别的样本点进行标注,随机抽取其中的820个样本作为训练集构建分类模型,其余4 651个样本作为测试集验证分类模型性能。选取RBF核构建Ms-SSSK分类模型,并结合7次交叉验证及网格搜索,遍历出最佳核函数参数值g为9.196,最佳惩罚因子c为16.489。
ϑ为空间光谱核权重系数,(1-ϑ)为原始光谱核权重系数,Ms-SSSK方法中的合成核形成时,参数ϑ的选取对分类精度会产生一定的影响[27],因此Ms-SSSK方法在区间[0,1]内以0.1为增幅进行权值的搜索,在每个ϑ值下运行5次实验程序并计算平均分类精度,找出获得最高平均分类精度的最佳ϑ值。针对测试集,不同权值ϑ下的分类精度如图6所示。

图6 权值ϑ对应的分类精度Fig.6 Classification accuracycorresponding to the weight ϑ
由图6可知,当ϑ为0或1时,代表最终分类核矩阵由单一核构成,并且单一原始光谱核分类精度为85.87%,低于单一空间光谱核分类精度91.79%;当ϑ从0递增至0.6时,测试集的分类精度承上升状态,当ϑ从0.6递增至1时分类精度开始下降,因此可以认为,当ϑ为0.6时分类精度最高,为98.53%。
由此可以看出,在基于Ms-SSSK方法的高光谱影像分类实验过程中,用于构建合成核的空间光谱核与原始光谱核都占有重要作用,并且空间光谱核的贡献率略高于原始光谱核。各类地物都有其独特的原始光谱特征,但是同谱异物、同物异谱的现象时有发生,Ms-SSSK方法中原始光谱特征占比较大时,具有较精细的空间光谱特征发挥不出优势,较易导致整体分类精度的下降,使用权值ϑ合理地分配空间光谱和原始光谱特征,可以极大地提高高光谱影像分类精度。
2.3 方法对比分析
当ϑ为0.6时,按照原来的c和g参数和训练集、测试集个数设置,将Ms-SSSK,Ms-FSSK,Ss-SSSK和O-SSSK这4种分类方法分别运行5次,得出测试集的平均分类精度和所有地物分类精度如表2所示。

表2 分类结果对比Tab.2 Comparison of classification results
从表2中可以看出,Ms-SSSK的分类精度最高,达到98.53%,O-SSSK的分类精度最低,为91.60%。相比于O-SSSK,Ss-SSSK的分类精度提升3.73个百分点;相比于Ms-FSSK,Ss-SSSK和O-SSSK这3种方法,Ms-SSSK的分类精度分别提高2.04,3.20和6.93个百分点。相比于现有深度学习方法[29],针对该数据集Ms-SSSK方法的分类精度提升了6.97个百分点。表2中的4种高光谱影像分类方法,采用Ms-SSSK得到的阴影、公路、草地的分类精度提升幅度较大,其中,阴影从O-SSSK的87.73%、Ss-SSSK的96.60%和Ms-FSSK的96.98%提升到Ms-SSSK的98.16%;草地的分类精度从O-SSSK的89.16%、Ss-SSSK的92.12%和Ms-FSSK的95.25%提升到Ms-SSSK方法的97.35%;公路的分类精度从O-SSSK的87.55%、Ss-SSSK的92.68%和Ms-FSSK的94.36%提升到Ms-SSSK方法的98.32%。4种模型的测试集分类结果如图7所示。由图7可以看出,数据集中阴影所占面积小且布局分散,当住宅面积较大时,极易将住宅与阴影分为一类;研究区中的林地与草地在空间格局上不够聚集且散布整个区域,并且二者具有较为相似的光谱特征,因此草地与林地在分类时易产生混淆;公路在整个区域中所占面积较大,并且与草地、林地,住宅等像元毗邻,因此分类时易被误划入上述地类。

(a)原始测试集 (b)Ms-SSSK (c)Ms-FSSK (d)Ss-SSSK (e)O-SSSK
Ss-SSSK方法将图像在一个尺度下进行超像素分割,无法判断最佳原始超像素个数,相较于多尺度超像素而言,无法考虑较为精细的图像特征信息;Ms-FSSK和O-SSSK方法采用滤波窗的方式获得图像空间光谱均值信息,然而最佳窗口的大小很难被确定,窗口过小无法包含全部重要信息,窗口过大会包含干扰信息,相较于超像素而言无法自适应均值计算区域;因此3种方法很难获得优于Ms-SSSK方法的分类效果。将在测试集上训练完成的模型用于分类原始图像,形成全区域分类结果如图8所示。并选取了2个典型区域用于分类细节信息对比,如图9所示。

(a)原始地物图 (b)Ms-SSSK (c)Ms-FSSK (d)Ss-SSSK (e)O-SSSK

(a)原始地物图1 (b)Ms-SSSK1 (c)Ms-FSSK1 (d)Ss-SSSK1 (e)O-SSSK1
O-SSSK方法针对大住宅附近公路的分类效果较差,并且易混淆草地和林地,如图8(e)和图9(e)(j)所示;Ss-SSSK方法可以大致对7种地物进行分类,但是缺少空间细节,如图8(d)和图9(d)所示;Ms-FSSK方法的分类结果中阴影细节较为明显,但是总体分类结果出现较多差错,尤其是公路与草地,如图8(c)和图9(c)(h)所示;Ms-SSSK方法考虑的图像特征较为精细,相比于另外2种方法,图像细节区分较为明显(如图8(b)和图9(b)(g)所示),获得了较高的地物分类精度。
为了继续探讨上述4类方法在不同规模样本集上的分类精度变化情况,分别从样本集合中随机抽取200,400,600和800个样本点用来训练模型,剩余样本作为测试集验证模型性能,针对不同规模测试集各模型的相对误差如图10所示。

图10 各模型相对误差结果图Fig.10 Relative error results of each model
从图10中可以看出,样本量从200递增到800,各模型的分类误差都在不断下降,且样本数目为200时,Ms-SSSK模型的分类相对误差在10%~15%内,与另外3个模型差距最大,随着样本数目的递增,分类精度差距逐渐缩小至2%~4.5%。该结果证明Ms-SSSK模型的空间光谱合成核方法能够在核空间中学习样本的相似性特征,进而融合图像多维特征,以获得较为精细充分的图像信息,在训练样本集规模较小时,依然可以获得较为理想的HSI分类精度。
3 结论
本研究针对高光谱影像具有的高维光谱特征信息,提出了耦合多尺度超像素空间光谱特征与原始光谱特征的Ms-SSSK分类模型,以Washington DC Mall高光谱图像为实验对象进行高光谱影像分类,并将分类结果与Ms-FSSK,Ss-SSSK和O-SSSK方法进行对比分析,主要结论如下:
1)Ms-SSSK方法得到的测试集分类精度为98.53%,相比于另外3种方法,该方法可以有效提升HSI分类精度,较易区分林地与草地等空间相邻且光谱特征相似的地类,有利于土地监管人员了解更为准确的地物现势信息。
2)多尺度超像素方法的运用,有利于提取更加精细的空间信息,并且能够减少最佳初始超像素个数对分类精度的影响。合成核的运用在注重图像空间关系的同时,合理利用丰富的光谱信息,使提取的特征更加全面。
3)在样本集规模很小的情况下,Ms-SSSK模型依然可以获得高于另外2种方法的分类精度,表明特征提取的全面性和精细程度在分类过程与分类精度有很大的关系。
Ms-SSSK方法能够有效解决图像光谱无法自适应、光谱信息获取不全面的问题,能够显著提升高光谱影像分类精度,对未来精准目标识别、地物准确分类、医学正确检测等具有重要意义。但是,不同地物具有不同的纹理特征,本文未探讨纹理特征在HSI分类中的影响,因此,在后续研究中考虑进一步结合图像纹理特征和空间光谱特征,研究出更高精度的高光谱遥感影像分类方法。
