起伏地表叠前深度偏移成像方法研究

宋 亮

（中国地震局第二监测中心，陕西 西安 710021）

随着地震勘探技术发展迅速，以及油气藏需求量的日益增长，地震勘探的方向已经从最开始的水平地表勘探转向起伏地表条件下的区域，例如山区以及海底等，这对地震勘探技术提出了新的挑战。起伏地表勘探中，激发点与接收点存在不确定性的高程差，这使以往的勘探技术以及资料处理技术已经不再适用，需要一种能适应起伏地表观测方式的特殊偏移成像流程。针对起伏地表勘探当中存在的诸多问题，许多学者做了大量研究，1979年Berryhill发表波动方程基准面校正法，并在1984年将其应用到叠前资料中；1984年Gazdag发表相移-插值法基准面校正法，能够适应介质横向变速较小的情况；1991年Reshef提出“逐步-累加”法，解决了地表起伏剧烈情况下对地下构造成像的影响；1992年Beasley等提出了“零速层”法；1999年Yang提出了“直接下延”基准面校正方法；2002年，何英提出了“波场上延”法。本文根据“波场上延”法的理论基础，实现了相移上延偏移成像与傅里叶有限差分上延偏移成像。

1 方法原理

1.1 波动方程基准面校正

波动方程基准面校正，是针对常规高程静校正的一种改进，解决了各种复杂地表条件造成的波形畸变问题，使地震成像精度大大提高。如图1（a）所示，波动方程基准面校正能够将地震波沿传播方向上延，真实地反映了波在介质中的传播过程。而图1（b）所示的高程静校正法则忽略横向传播，存在较大误差。

图1 基准面校正射线路径示意图

1.2 “波场上延”法

“波长上延”法是波动方程基准面校正法的一个分支，经过数次改进而来的较为成熟的基准面校正法，其建立在零速层法以及“逐步-累加”法的理论基础上，其具体实现思路为：将基准面设定在观测面的最高点或者最高点之上的水平面，然后将野外观测的波场数据向上延拓到所定义的基准面，经过这种处理之后，就可以将起伏地表观测的数据校正为水平面观测的地震数据，消除起伏地表带来的时距曲线畸变。在基准面校正过程中，实际观测面与基准面之间的速度一般选取低降速带速度进行计算。在“波长上延”过程中，可选取相移波动方程或傅里叶有限差分法等不同的延拓算子进行波场延拓，以适应不同的地质情况，保证计算效率以及精确度。

相移波动方程只能适用于简单的地下结构情况，但其过程能够清晰表达波长延拓的原理，因此以相移法为例表达“波长上延”过程。

波场在二维情况下的传播方程为：

上式中，P为波场记录P（x，z;t），t为时间，v为横波或纵波的传播速度。

为方便计算，令式（1）分别对x，t做二维傅氏变换，可得：

以介质横向速度均匀为前提，则式（2）可以在每个延拓步长中，在频率-波数域直接求解，即：

上式中，c1、c2为待定常数，此时的波场依然是耦合的。根据前文所推导的解耦延拓算子，在进行波场延拓前，对上、下波场进行解耦，得到：

从而可推出频率波数（F-K）域内的向上、下波场相移延拓表达式：

2 模型试算

2.1 水平地表倾斜地层模型试算

为验证本文所推导波场延拓算子以及程序正确性，此处设计一在水平地表激发并接收的简单斜层模型，图2（a）是斜层纵波速度模型，模型长度x=500m，深度z=500m，网格间距dx=dz=1m，纵波速度的最小值和最大值分别是1000m/s和2000m/s。利用分区多步LTI射线追踪正演波场记录，波场记录总共40炮，第一炮位于0m处，最后一炮位于312m处，炮间距是8m，均采用左侧零偏放炮方式，每炮48道接收，道间距是4m；采用60Hz主频的雷克子波作为震源，采样间隔2ms，采样长度是630ms，延拓步长取3m，延拓深度为498m。图2（b）是其1~3炮炮集记录。利用相移延拓算子与傅里叶有限差分延拓算子分别进行偏移成像试算，对比两种算子的偏移成像准确度与运算效率。图3（a）为相移算法偏移成像结果，图3（b）为傅里叶有限差分法偏移成像结果。表1是两种方法的计算效率对比。

图2 倾斜地层理论模型及正演记录

由图3（a）和图3（b）可知，相移法偏移成像和傅里叶有限差分法偏移成像，都可以得到准确的成像结果，并且成像结果相似，证明了本文所设计的偏移成像算法的正确性。但由表1可得出，对于同一倾斜层模型，相移法偏移成像的计算效率远高于傅里叶有限差分偏移成像，因此对一些横向速度变化简单的简单模型，可以用相移法偏移成像，在保证成像准确度的同时，可以大大提高计算效率。

表1 相移法与傅里叶有限差分法计算效率对比

图3 倾斜地层偏移成像结果

2.2 “波场上延”法模型试算

为验证“波场上延”基准面校正法的有效性，设计一简单起伏观测面速度模型用于数值模拟，并以相应的水平地表模型进行对比分析。如图4（a）是水平观测面纵波速度模型，图4（b）是起伏观测面纵波速度模型，两模型基本参数一致，均为长度x=400m，深度z=400m，网格间距dx=dz=1m，纵波速度最小值和最大值分别为1000m/s和1500m/s。两模型利用分区多步LTI射线追踪正演计算得到炮集记录，正演炮集记录共1炮，炮点位于x=0m处，采用左侧零偏放炮方式，单炮101道接收，道间距是4m；采用60Hz主频的雷克子波作为震源，采样间隔1ms，采样长度是1300ms。不同之处在于图4（a）水平模型的激发与接收均在x=0的水平面上，而图4（b）起伏模型的震源、检波点都位于地表S1上，基准面设为地表最高点所在水平面R1，即x=0平面上。图5（a）为水平模型的正演单炮记录，图5（b）则为起伏模型的正演单炮记录。分别用800m/s、1000m/s、1200m/s作为上延速度场进行波场上延基准面校正，分别得到如图6（a）、6（b）、6（c）所示结果。

图4 理论速度模型

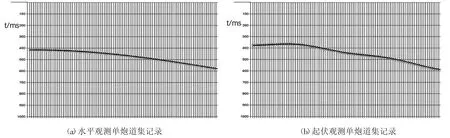
图5 正演单炮道集记录

图6 基准面校正结果

由图5（a）可以看出，在水平面激发与接收的条件下，其单炮地震记录为规则的双曲线，其对应的是图4（a）的水平地表模型。而在图4（b）中，激发与接收都在起伏地表S1面上，最终得到的单炮地震记录为图5（b），其几何特征已经远非双曲线形态。基准面校正的过程，也就是将波场由S1面校正到水平面R1，在波场上延校正过程中，需要在校正路径中填充速度场，分别选择800m/s、1000m/s、1200m/s，得到图6（a）、（b）、（c）三种校正结果。可以看出，无论是选取800m/s还是1200m/s作为上延速度场，最终校正结果皆与双曲线特征有肉眼可见的差别，如图6（a）与图6（c）所示。只有当校正速度为1000m/s，最终得到如图6（b）所示的单炮道集校正记录，才几乎完全恢复双曲线特征。由此可见，波场上延基准面校正法中，校正速度的选取尤为重要，最好选取与近地表低速带相近的校正速度，才能够得到较为准确的校正结果。在理论模型试算时，由于近地表速度已知，因此校正速度的选取较为简单，能够得到较好的校正结果。在处理实际资料时，需要尽可能获得足够精确的近地表或近海底速度，才能够选取较为恰当的校正速度场，从而进行最为精确的基准面校正，达到简化波场特征和提高地震资料横向分辨率的效果。

2.3 起伏地表模型试算

为验证本文设计起伏地表叠前深度偏移成像流程的正确性，设计一起伏地表理论模型，炮点与检波点不在同一水平面。如图7所示为一起伏地表理论纵波速度模型，横向x=4000m，纵向z=3500m。该模型最上层速度1500m/s，下方地层速度最小为2000m/s，最大3500m/s。炮集记录采用LTI射线追踪正演得到，共160炮，第一炮位于x=0，y=0处，炮间距25m，每炮60道接收，检波器为起伏地表固定放置，第一道x=500m，z=200m，道距50m，最后一道x=3500m，z=200m。采样间隔0.001s，采样长度1000ms。图8为起伏地表观测方式下第1~3炮地震记录。对起伏地表观测方式下的地震波场采用“波场上延”基准面校正法，以傅里叶有限差分波场延拓算子进行校正，得到校正后的地震记录，就如同从海面激发与接收的地震记录，如图9所示为1~3炮地震记录经基准面校正后结果。以校正后的地震记录进行偏移成像，其中延拓步长为10m，延拓步数340。

图7 起伏地表理论速度模型

由图8与图9对比可知，经过波场上延法基准面校正后，原本的地震记录反射同相轴具有的非双曲畸变已经得到修正，较好地消除了炮检点高程不一致对地震记录带来的影响。以校正后的地震记录进行后续偏移成像，即相当于在水平表面激发并接收，分别用相移算法与傅里叶有限差分算法进行成像，得到如图10（a）与10（b）所示结果。对比两种算法的成像结果可以发现，两种偏移算法都能够得到较为准确的成像结果，但利用傅里叶有限差分偏移算子得到的偏移成像结果比相移偏移算子得到的成像结果更加清晰，并且傅里叶有限差分算法的成像剖面噪声也更低。相移延拓算法的计算效率高于傅里叶有限差分延拓算法，这是成像算法高阶运算带来的必然结果，因此在进行地震记录的偏移成像运算时，需要选取合适的延拓算法，来满足不同要求下的成像精度与计算效率。

图8 第1~3炮原始地震记录

图9 第1~3炮地震记录基准面校正结果

图10 起伏地表模型偏移成像结果

由本节对起伏地表模型的测试结果可以得出，建立在“波场上延”基准面校正法基础上的波动方程叠前深度偏移成像方法，不仅可以消除炮检点高程起伏带来的地形影响与观测方式影响，更可以较好地对地下复杂构造进行较为精确的成像，起到解决观测表面与地下介质双重复杂地质条件的问题，得到较好的偏移成像结果。

3 结论

（1）“波场上延”波动方程偏移成像方法，利用波动方程波场延拓的方法，将炮点与检波点延拓至同一水平面，然后用常规水平地表偏移成像方法进行后续处理，可以很好地消除起伏地表地震勘探中炮检点高程不一致带来的波形误差，是实现起伏地表地震勘探成像的有效手段，能够得到良好的成像结果，具有非常广阔的应用前景。

（2）波动方程基准面校正法可以同时解决炮检点起伏的问题与介质横向变速严重的问题，这是因为传统高程静校正只做了简单的垂直时移处理，波动方程基准面校正则将野外静校正包含其中，最终的校正量同时包含了旅行时以及波场的水平分量和垂直分量，最终的偏移成像结果精度更高，更为准确，是今后基准面校正方法的主要发展方向。

（3）波场延拓算法对于最终成像结果和计算效率影响巨大，在面对不同的地下结构情况时，需选取恰当的延拓算法，可以在保证偏移成像准确性的同时，提高算法的效率。