基于傅里叶变换下的水银测量元件的特性研究

刘宇轩，杜 苗，王 菁

（天水师范学院 电子信息与电气工程学院，甘肃 天水 741000）

对于传统的水银温度计而言存在着水银膨胀系数的误差、毛细管直径不均匀的误差、毛细管刻度的误差、热滞后的误差、露茎的误差等问题[1]。但是文章重点讨论水银本身性质上的问题。利用傅里叶分析，并且通过设计一个补偿系统和去噪系统，可以有效地提高水银温度计的精度与使用效率。在家庭生活方面占据着不可忽视的地位，可以大大降低判断身体温度的失误率。

1 傅里叶级数[2-3]（Fourier Series）

对于一个由成谐波关系的复指数，是一种通过线性组合而成的信号，见式（1）：

式（1）称为傅里叶级数。此处ak的表达式为式（2）：ak为傅里叶级数系数（Fourier Series Coefficient）。

2 傅里叶变换[2-3]（Fourier Transform）

用傅里叶级数来表示一个周期信号时，当周期T逐渐增加时，该信号的基波频率就会相应减少，对应的成谐波关系的各个分量在频域上也会逐渐靠近；那么进一步的扩展开来，当周期T趋于无穷大的时候，这些频率分量也就变成了一个连续域，从而在傅里叶级数求和的过程中，就演变成了求积分的问题。

对于一个信号x（t）来说，形如：

就称为对函数x（t）进行傅里叶变换。那同样的，它的逆变换为：

式（3）和式（4）称为傅里叶变换对（Fourier Transform Pair）。函数X（jw）称为x（t）的傅里叶变换或傅里叶积分（Fourier Integral）。则函数x（t）为X（jw）的逆变换，所以式（4）称为傅里叶逆变换（Inverse Fourier Transform）。傅里叶变换是一种对于信号进行分析的工具，它既可以分解和分析信号，也可以将分解的信号合成为一个信号。一般情况下，傅里叶变换是用正弦波充当信号的主要成分。

3 逆系统（Inverse System）

当H（jw）*Y（jw）=1时，则这两个系统互为逆系统。假如该系统在不同的信号激励作用下产生了不同的响应，那么则称该系统为可逆系统。并且对于每一个可逆系统来说，都存在一个逆系统。当原系统与这个逆系统级联后，输出信号与输入信号则相同。

4 补偿系统的设计（Design of Compensation System）

当把测量装置的输出提供给该补偿系统时，其所产生的输出等于待测量液体的瞬时温度。假设这个装置对温度的响应为单位阶跃响应，见式（5）：

则该响阶跃应的冲激响应，见式（6）：

该系统的频率响应，见式（7）：

现在需对上方系统构建一个逆系统，因此该逆系统的频率响应为G（jw），见式（8）：

对G（jw）进行傅里叶逆变换得到式（9）：

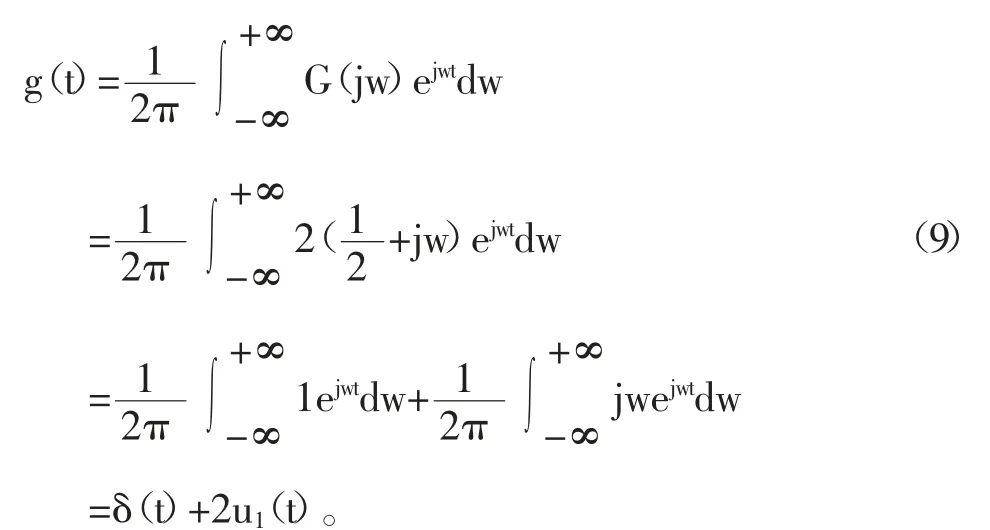
5 误差分析（Error Analysis）

在周期信号中存在均方误差，即

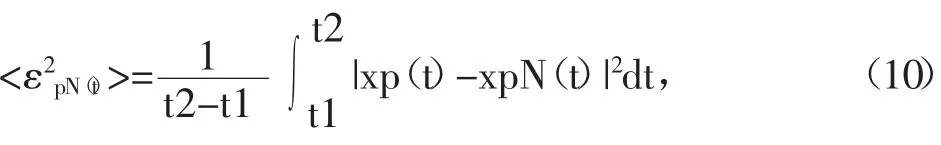
周期信号的最小均方误差为

在把逆系统作为测量装置的补偿器时，常常发生的一个问题是：如果由于装置内部发生了微小而且还无规律的一些现象，比如分子运动、化学变化等等[4]。就导致了测量装置的实际总输出可能会包含有一定程度的误差，那么也可能会产生相对较大的读数误差。尤其对于温度计这样一种很敏感的医疗测量工具来说是无法接受的。但是往往在实际的系统当中，这种误差源总是存在的，因此就必须要将这些误差纳入到考虑范围当中，也就是要进行误差分析。为了证明这一点，现在研究一个测量装置，假定它的总输出还是可以用式（5）所表示的测量装置的响应s（t）与干扰“噪声”信号n（t）之和来表示和模拟。该模拟的模型图见图1。

图1中包括了逆系统，该系统以测量该装置的总输出作为输入。假定n（t）=sin（wt），那么当n（t）通过该逆系统时，经傅里叶分析的计算可得输出p（t）为式（13）：

图1 误差分析的模型图

显然输出是直接取决于w的取值，跟其他的值无关，满足该系统为线性时不变系统这个条件。因此，随着w的增加，噪声对输出的影响也会增大。

6 去噪系统（Denoising System）

对于水银来说，水银容易受到紫外线、辐射、高频场直射等干扰[4]，也就是干扰“噪声”信号。干扰“噪声”信号在许多线性时不变系统分析应用中是一个很重要，而且绝对不可忽视的问题。具体而言，要在系统的响应速度和系统抑制高频干扰的能力之间进行基本的平衡。这种平衡意味着，如果提高测量装置的响应速度，也就是采用前面所述加入一个逆系统。那么就产生了一个把那些不需要的正弦信号也放大了的系统。为了进一步说明，考虑一个测量装置，它对被噪声污损了的温度变化做出了瞬时响应。这个系统的响应模型图见图2。

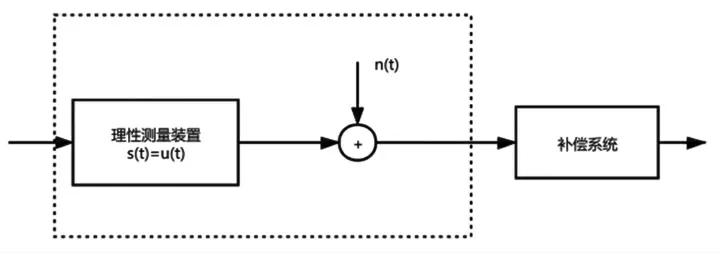
图2 去噪系统模型图

即该系统的响应可以利用理想化测量装置的响应与污损信号n（t）的响应之和来表示。假如我们希望设计一个新的补偿系统，该补偿系统的作用就是可以减慢对实际温度变化响应的同时，也衰减了噪声n（t）。设这个补偿系统的单位冲激响应（Unit Impulse Response）为式（14）：

使得图2的总系统在对噪声n（t）=sin6t所产生的输出幅度不大于1/4的情况下，对温度阶跃变化的响应尽最大可能的快。

对该系统的响应进行傅里叶变换得：

当|H（jw）|2≤，恰好当w=6的时候，即的时候，就可以得到。此时这个范围内的a的取值才能使图2中的总系统在对噪声n（t）=sin（wt）（w值取6的时候）所产生的总输出幅度不大于的条件下，对温度的阶跃变化的响应加快。也就是使得水银温度计受外界干扰的程度降低，那么自然该系统就稳定、精确。

7 结束语

对于温度计当中水银的一些特性，按照传统的温度计来看，该温度计是无法快速做出反应的，但是利用傅里叶分析进行改进的话，可以最大限度地避免光线、热辐射等[4]问题对它的影响，使得该温度计会更加灵敏、测量精度更加高。通过设计一个补偿系统和去噪系统，在水银温度计的灵敏度方面得到了很大提高，在日常家庭生活当中起到不小的作用。