基于QCSP和NSGA-II的产品质量参数鲁棒性设计
2021-09-23王宇星朱伏平曹婷婷
王宇星,朱伏平,曹婷婷
(西南科技大学制造科学与工程学院,四川 绵阳621010)
1 引言
目前的机械产品质量参数设计,都在假定条件中认为整个生命周期内设计参数没有受外面因素扰动。然而事实上,机械产品在生产阶段中由于受到不确定性因素影响,产品的质量参数会产生变差,输出质量参数不稳定,为企业带来难以估量的损失。鲁棒(robust)设计也称田口方法,由日本学者田口玄一提出,将质量重点由生产制造过程向前推移到产品设计过程,强调设计对质量的重要作用[1]。可以调整设计参数及控制其容差,使产品的质量特性对各种不确定要素的随机扰动,产生较强抗干扰能力。机械产品特性会更稳定,质量也会更可靠。若机械产品设计方案即便在各种因素的扰动下,质量特性也是稳定的,就认为其具有鲁棒性。进行鲁棒设计可以使机械产品在生产过程中很大程度上保证质量参数的鲁棒性。
国内外学者对于鲁棒特性设计的探索,按不确定要素处理方式可分出两种,其中一种是概率鲁棒设计。文献[2]设计了一种适用于电力系统组件多参数指标的鲁棒优化方法。采用概率方法表达了驾驶条件的不确定性,设计了电力系统的试验参数。文献[3]考虑了随机因素对弓头支撑疲劳寿命的影响,分析了各变量的概率分布特征,提出了一种基于6σ鲁棒优化设计的方法。文献[4]提出了一种用于齿轮设计宏观和微观几何参数的多目标优化方法。对于齿轮设计,使用一千个随机制造误差样本进行蒙特卡罗模拟,以评估对制造误差的稳健性。每个嵌入刚度的有效值和STE的波动由概率密度函数描述。文献[5]确定了网络物理经验方法的概率鲁棒保真度,提出了一种基于建模和主动学习的替代方法的计算方法,并利用薄海洋结构的主动截断问题测试了效率。另一种是非概率鲁棒设计。文献[6]提出了区间变量和随机变量共存设计问题的可靠性指标,定量表征了设计方案的稳定性程度,构建了具有区间概率的混合鲁棒优化模型。文献[7]将可靠的参数设计思想与多目标理念相结合,创造了一个多维多目标模型,提高了弹簧参数的可靠性。文献[8]结合蒙特卡罗模拟和人工神经网络,提出了一种基于汽车手柄设计建模的RBRDO搜索方法。搜索方向基于设计变量和响应之间的相关系数,并选择最佳搜索方向和步长。文献[9]借助第一通道理论定义了非概率时变不确定性下的混合可靠性测度,提出了一种混合时间依赖可靠性模型,研究了基于混合时间相关可靠性的新优化策略。
综上所述,概率鲁棒设计要求获得不确定要素的概率分布规律或者函数,在鲁棒性优化中包括概率信息的计算,工程应用复杂,并且建模所需的概率分布和统计信息在工程应用中不容易获取。而非概率鲁棒设计方法不必要获得不确定要素的概率信息,但是需要模型中的目标和约束函数连续且可导。因此,本文运用基于量词约束满足问题(Quantified constraint satisfaction problem,QCSP)的鲁棒优化设计方法。该方式不需要获得概率分布和统计信息,创建的模型对函数的可导性没有要求,具有一定的优越性。
2 质量特性问题
产品质量可被理解为产品的“特征”满足客户的“要求”的程度。“特征”包含多个方面:性能,可信度,安全性,适应性,经济性和时间管理等,记为Y=(y1,y2,…,ym)。产品在生产阶段中受到一些不确定要素的影响,包含一些不可控要素。不确定因素可引起产品在工艺设计过程中的设计参数p产生偏差Δp=(Δp1,Δp2,…,Δpk),进而导致质量特征值yj产生改变,记为y′i。鲁棒优化设计的目标,就是产品质量特性在设计参数存在Δp变差的状态下,仍可以符合工艺设计约束的要求,并确保y′i的变差在允许范围内,在此约束条件下计算y′i的极值。因此,产品鲁棒优化设计获取的质量设计方案对不确定要素的影响才有较小的灵敏度,且产品的质量特性值同时满足于工艺设计约束,甚至更优于由经验设计得到的方案。
3 QCSP模型描述
3.1 存在性变量和普遍性变量
QCSP模型的变量包含有设计参数变量和噪声参数变量。设计参数变量是产品设计中主要关键尺寸的变量,噪声参数变量则是设计参数的变化值。以QCSP模型表达变量为QV=∃X⋃∀ΔP,式中X是设计参数变量,Δp是噪声参数变量。产品质量参数鲁棒优化问题中的所有设计参数变量为X={x1,x2,…,xn},这些是QCSP模型中的存在性变量,且要求变量具有独立性;噪声变量即设计参数变差为普遍性变量。
值域D由X和Δp的自变量定义域构成,也称之为优化设计的搜索域。质量参数鲁棒优化设计在设计参数波动范围给定状态下,通过满足约束计算设计变量的可行解,因此可行域Ds包括设计参数变量的值。
3.2 模型约束
QCSP模型的约束包含目标函数约束和设计参数约束。数学形式表达如下:

(1)目标约束
式中:yi(X,P)-≤0—质量特性目标约束,yi(X,P)—模型中的目标函数—目标函数值。由于噪声变化量Δp的扰动,设计参数变成了区间变量,根据区间函数理论得出,目标函数yi(X,P)变成了相应的区间函数Yi(X,PI)。对应每个解sj,有则sj∈Dsolution的条件为
(a)鲁棒性要求设计参数变化在允许范围之中,即Yij的区间宽度为为预先设定的Y的最大波动。
(b)在符合以上两个前提的Yij里选最优,即选择最小的值。Yi为区间数,会涉及区间数之间的大小比较。
(2)设计约束
设计参数约束主要包括产品参数信息,关乎产品质量特征的功能满足和结构要求等。式(1)中的gj(X,P)≤0是不等式设计约束,hk(X,P)=0是等式设计约束。若设计参数是区间数,那么约束函数就变为了对应的区间函数Gj(X,P)和Hk(X,P)。
(a)对于原不等式约束gj(X,P)≤0,现有在对照这两区间的值时,一个区间变为了0,可得到小于0的概率,如公式(2)所示:

P(Gj≤0)=[0,1]是QCSP模型设计约束的鲁棒性指标。求目标函数的值是本模型的重点,因此某些参数约束条件可以有相当程度的不符和。需要不等式约束的鲁棒性大于等于ξj,那么不等式设计约束可以表达为:1,2,…,β。
(b)对于原等式约束hk(X,P)=0,现有给定等式约束波动范围则Hk位于区间的概率,如式(3)所示。

设计要求约束鲁棒性大于等于ςk,那么等式设计约束可表达为:
3.3 鲁棒解概念表达
对于QCSP模型,产品质量参数设计求得的解si不仅要求是有效的且要确保在设有噪声扰动Δp的状态下,设计参数约束和目标函数约束同时达到符合,那么称si为鲁棒解,称为srobust。根据量词概念理论描述鲁棒优化的QCSP模型如下:

式中:QV=∃X⋃∀ΔP,QV—模型变量,Q∈{}∃,∀,∃—存在和∀表示所有。X—设计变量集;ΔP—因为噪声干扰引起的设计参数的波动范围。若QCSP模型存在有效的鲁棒解,则可表示如下:
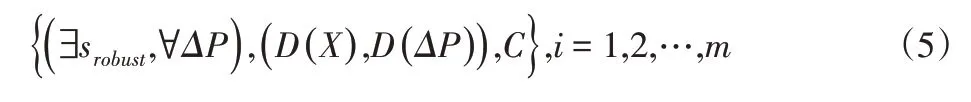
4 NSGA-II求解算法
NSGA-II算法由Srinivas和Deb在NSGA算法的基础上改进完善,使用快速非支配排序算法大大降低了复杂度。它使用拥挤度和拥挤度比较算子来扩展准帕累托域中的个体,并使得个体保持均匀分布。取代了共享半径Qshare,保持了种群的多样性。它还设定精英策略,扩大了样本的采集空间,防止遗失最优个体,提高计算效率和算法的鲁棒性程序流程,如图1所示。

图1 NSGA II算法流程图Fig.1 NSGA II Algorithm Flow Chart
5 应用案例
5.1 压力机的质量参数鲁棒优化模型
机械压力机普遍用以锻压、挤压、冲压和粉末冶炼等工艺,在数目上约占各种锻压机械总和的一半以上,具有动作平稳,作业可靠等优点。它的工作原理是通过电动机的旋转,带动曲柄滑块机构中的滑块做上下往复运动,锻压配料成形。
某型号曲柄连杆压力机的设计要求为滑块的拉深深度大于250 mm,行程为1000 mm,在工作过程中,连杆等构件不能发生干涉且须使得滑块在拉深范围内速率趋向稳定。如图2所示,杆l1是主动件,电动机带动杆l1匀速转动,经过其余连杆间相互传动,使得滑块在纵向做往复运动。θ′为杆l3与杆l4之间的夹角,θ″为杆l6与杆l7之间的夹角。x0,y0分别为两固定支点在x轴与y轴上的距离。

图2 曲柄连杆机构简图Fig.2 Schematic Diagram of the Crank Linkage Mechanism
曲柄连杆压力机拉深质量参数设计要领总体上有如下两方面:
(1)压力机拉深深度设计要求
如图2所示,运用解析法分析曲柄连杆结构的运动,滑块位移计算公式如下:

式中:H=-l1sinθ+l7cosε6+l8cosε7,θ—l1与x轴正向的夹角,ε6,ε7满足

滑块的拉深范围相对应在曲柄连杆机构运动的下死点前100°范围内,由此得到滑块在拉深结束时的曲柄转角,因此,产品质量特征的第一目标函数计算公式为:

转化为最小化问题为:

式中:θ*—滑块机构拉深至机构下死点时的曲柄转角。
(2)压力机拉深速率波动设计要求
为确保锻压工件的表面质量,在滑块拉深范围内,必须控制滑块的速率波动。因此,由曲柄转角筛选相等间隔的转角角度求解滑块在拉深过程中的速率波动,公式如下:
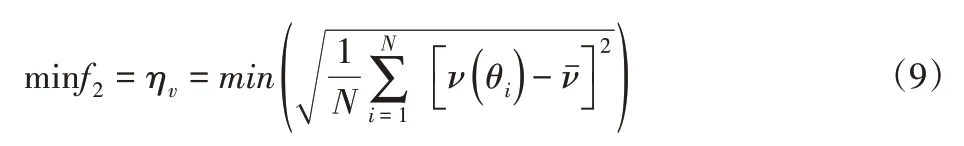
式中:N—滑块在拉深中平均取值的个数,νˉ—滑块平均拉深速率。
为确保拉深部件的质量特征,滑块允许的行程偏差为ΔS≤1mm,即
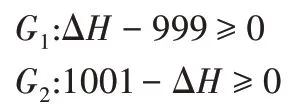
QCSP模型的设计变量除了符合约束上下限外,还应该符合曲柄连杆机构中存在曲柄的前提,即曲柄的杆长最短,且最长杆与曲柄杆长的总和应小于另外两根杆的杆长,约束表达公式如下:

同时,为了确保该曲柄连杆机构具有较高的效率,必须使机构的连杆l2和l3间的夹角δ∈[40,140]

由于锻压工件在滑块拉深中受材料特性的限定,为确保产品合格率,滑块的最大拉深速率不能超出许用拉深速率,公式为

式中:[ν]—滑块的许用拉深速率,当滑块每分钟14次往复运动时,规定最大许用拉深速率是25 m/min。
建立机械压力机质量参数的鲁棒优化模型,以几何参数l1,l2,…l8,θ′,θ″,x0,y0作为设计变量,首先不考虑噪声扰动,针对设计变量建立模型如下:

实际生产制造阶段中,由于受到多维不确定性要素的干扰,连杆的杆长及杆间夹角角度存在波动,式中上下拉杆的杆长、和上下摇杆之间的夹角生成的设计参数波动范围为Δp,长度偏差范围为1 mm,角度偏差范围为0.50,即Δp={( Δl2,Δl5,Δθ″):-0.5≤Δl2≤0.5,-0.5≤Δl5≤0.5,-0.25°≤Δθ″≤0.25°}曲柄连杆压力机在锻压工件时,滑块的拉深深度和速率波动因为波动所造成的质量特征允许误差为Δf=( Δf1,Δf2)=( 5mm,5mm/s)。考虑了噪声扰动造成的设计参数波动范围Δp,建立鲁棒优化的QCSP模型如下:
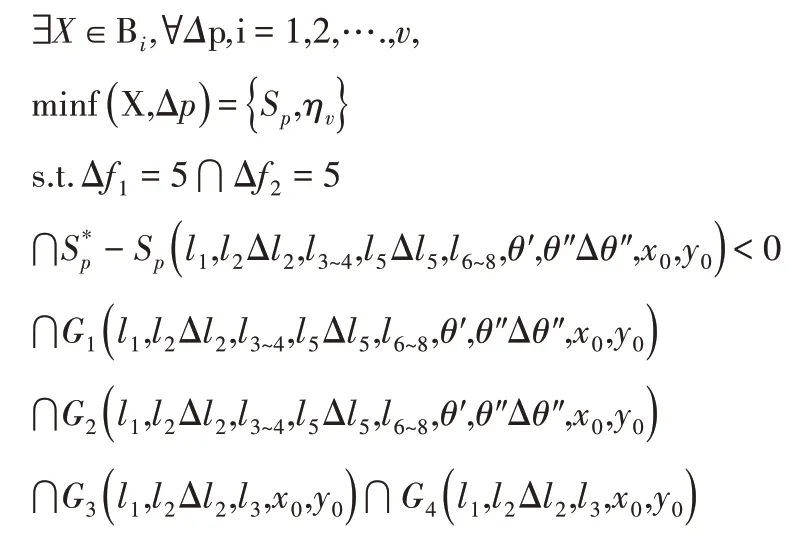

式中:X=(l1,l2,…l8,θ′,θ″,x0,y0)—设计变量集。模型里有10个不等式约束条件,分别记为约束条件(1)-(10)。前面三个为质量参数的目标函数约束;后面七个约束为设计参数约束。对于约束(4)-(7),由于设计参数波动的存在,在优化改善中需对其度量鲁棒性指标,记其鲁棒性指标为P(Y1≤0),P(Y2≤0)和P(G1≤0)(约束均转化为Yi≤0或Gi≤0的形式)。根据设计要求,鲁棒性指标需满足P(Y1≤0)≥ξ1,P(Y2≤0)≥ξ2及P(G1≤0)≥ξ3,其中ξ1=1.00,ξ2=1.00,ξ3=0.90,由此可见目标约束必须得到完全满足。
5.2 压力机质量特性鲁棒优化实现
以某型号的压力机作为参数设计的算例,根据设计行业规范,详细设计参数变量原始值及变量取值范围,如表1所示。

表1 原始设计值及上下限Tab.1 Original Design Value and Upper and Lower Limits
最低设计要求=250。利用算法鲁棒性强的特点,搜索鲁棒解,令迭代次数Gmax=500,生成初始种群规模为S=500,交叉概率设定为0.8,变异概率设定为0.1。运用Matlab 2016b对模型优化求解,运行环境为Core(TM)i5-3230M(2.6 GHz),8GB内存系统。求解结果,如图3所示。

图3 曲柄连杆压力机鲁棒优化解Fig.3 Robust Optimization Solution of Crank Connecting Rod Press
由图3可知,拉深速率波动幅度随着拉深深度的增加而变大,滑块拉深深度在[10,25]范围内,拉深速度波动变化比较平缓。通过NSGA-II算法鲁棒优化求解,得到33个表征压力机关键尺寸参数的Pareto设计解。
根据基于信息熵的优选理论,Pareto的解χi的熵权计算公式如下:
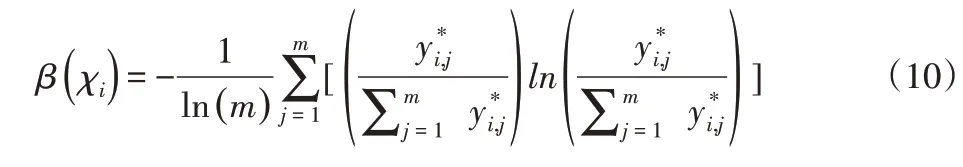
式中:m—优化目标的个数;yij—χi在第j个优化目标上的取值,yij是区间值当的中值,即对yij规范化和标准化处理后得到的值。β(χi)越大,说明该解在各目标上的分布多样性越小,总体性能越好。利用公式进一步优选,计算每个非支配解的熵权,选出信息熵最大值β(χ20)=0.7533,其对应的压力机滑块拉深深度和拉深速率波动分别为Sp=274.6,ηv=5.24。设计变量值,如表2所示。
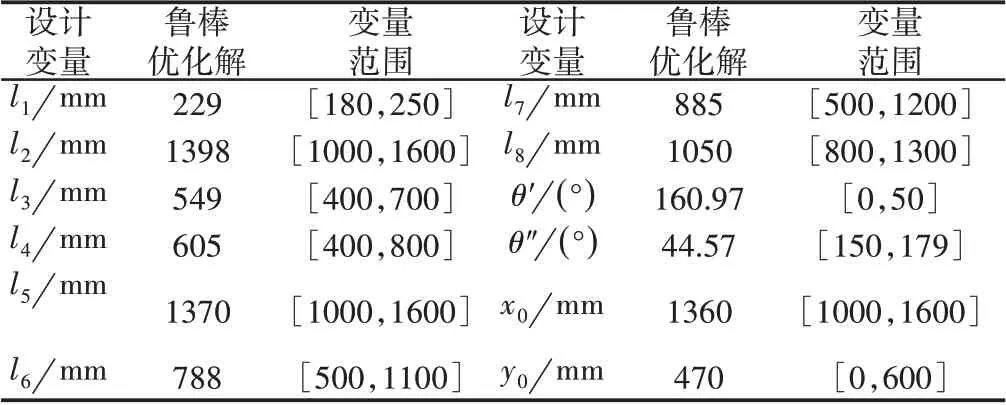
表2 压力机鲁棒性优化解Tab.2 Robust Optimization Solution of Press
表3针对压力机参数优化的鲁棒设计方案和初始方案,在质量参数值、质量参数波动及约束鲁棒性这些地方做了对比。该鲁棒优化方案以损失一小部分设计参数约束的鲁棒性的代价,使得完全符合目标函数约束且减小了质量参数波动,分析得出优化方案远优于原始方案。通过比较,鲁棒优化方案的解相比于原始设计,对设计参数变差敏感度低,使得压力机的拉深性能具有较高的鲁棒性。

表3 优化方案与原始方案对比Tab.3 Comparison Between Optimization Scheme and Original Scheme
6 结论
本文针对机械产品的设计参数由于设备生产阶段中受不确定要素扰动引起的质量参数波动变化问题,在QCSP理论基础上建立了产品质量参数鲁棒设计的优化模型。采用了鲁棒设计获取使产品质量鲁棒性较高的Pareto最优解。并采用NSGA-II求解模型得Pareto解集,结合模糊信息熵权理论选最优。最后应用该方法对某型机械压力机的拉深性能质量参数进行优化设计,通过对比优化解与初始解的鲁棒性指标,验证了方法的有效性。
