基于有限元分析耐高压试验观察装置设计

刘 洋，崔立军

（1.天津职业大学机械工程实训中心,天津30022；2.天津职业技术师范大学工程实训中心，天津300410）

1 引言

耐高压试验观察装置主要用于模拟深海试验装置受力情况，最高可以模拟7000米海水的压力作用，便于研究观察窗受海水循环压力作用时的应力、应变和疲劳及裂纹的情况［1］。该装置可有效改善目前标准试验的缺陷，可以针对具体的海水压力情况进行模拟试验，使得试验研究更能接近海试过程中观察窗的受力情况。因此对耐高压试验观察装置进行设计分析，具有重要的应用价值。

国内外学者对此进行了一定的研究：文献［2］研究不同的密封装置对海底耐高压观察窗的受力影响；文献［3］基于软件模拟，分析不同的参数对观察装置密封圈Von Mises应力的影响规律；文献［4］采用等效试验研究观察装置的受力情况；文献［5］采用试验方法分析密封装置在深海的受力状态，为优化设计提供参考。

针对应用于圆锥形观察窗研究的试验用耐高压观察装置进行设计，对比球壳型和圆筒型压力装置的优缺点，选取圆筒型进行尺寸设计，基于有限单元法对结构强度进行分析；对密封装置进行设计，选取O型圈结构，利用Marc软件对O型圈进行密封分析，获得最佳密封间隙和压缩率；并对密封间隙和压缩率对O型圈应力的影响进行分析；根据设计最大加压情况，对连接装置和加压装置进行设计；对比实测观察窗主轴位移拟合值与理论分析、仿真分析结果的差异，验证装置的可靠性。

2 试验装置设计

针对观察窗应用于深海设备，所受的海水压力较大，可以承受80Mpa的试验压力，要求具有良好的密封性，可以同时进行大小两种尺寸的观察窗试验［6］，因此，设计球壳型和圆筒型压力装置模型，如图1所示。

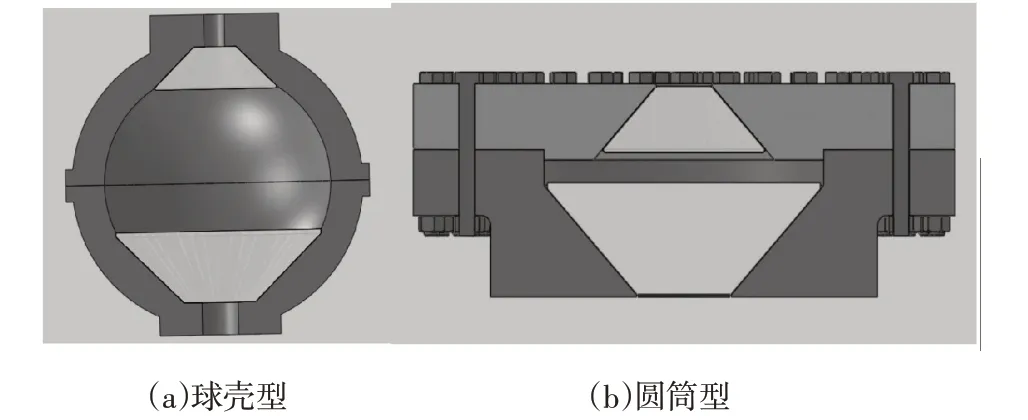
图1 观察试验装置模型Fig.1 Observation Window Pressure Device Model

图1（a）所示的结构可将大观察窗和小观察窗放在同一个压力容器进行试验，这样不仅可以正确模拟大小观察窗在海底受压的情况，而且避免单独对大观察窗和小观察窗进行试验，可以减少压力试验的次数，较少试验步骤。图1（b）中所示为该结构将大观察窗和小观察窗在压力装置中安放的位置，因为压力容器和大小观察窗之间充满介质。

2.1 尺寸设计

海底7000m深海压力约70MPa，为了避免安全系数重复，取设计压力为80MPa。取压力装置的内径为650mm，此时所设计容器为高压容器，所以根据强度理论，得到球壳类压力容器的壁厚为：

式的使用范围：p≤0.6［σ］φ，若p=80Mpa，则壁厚结果为72.22mm。

筒状压力容器的壁厚为：

式中：δ—容器壁厚，mm；Di—圆筒容器内直径，mm；［δ］—材料许用应力。Φ—设计温度下材料强度减弱系数。根据计算，得到筒状压力容器的壁厚为160mm。

圆筒状压力容器制造较为简单，成本较低，所以本次试验采用圆筒状结构设计压力容器，在压力容器的尺寸设计上，要考虑到大观察窗和小观察窗的位置及尺寸，保证大观察窗和小观察窗合理放置［7］，同时尽量减少液压油的占用空间，因为大观察窗为最大受力面，直径为634mm，则将内径设计为650mm。

2.2 有限元分析

装置主要用于测试海底7000米处观察装置所有的压力，在此深度的深海压力约70MPa，考虑到安全因素，取设计压力为80MPa，此处在受压面施加的载荷为80Mpa的压力。采用普通结构钢做压力装置的材料［8］。根据尺寸，建立壁厚为160mm、外圆直径为900mm的三维模型，对球壳型压力容器进行有限元分析。上下盖板，在7000米压力下的应力应变，如图2所示。

图2 应力和应变结算结果Fig.2 Stress and Strain Settlement Result

根据图3有限元分析结果可知，最大应力值为114Mpa，最大应变为0.010527mm，上盖板和下盖板的危险截面均出现在底部开口位置，且整个压力装置最危险的截面出现在安装大观察窗上盖的底部。可以改善此位置的结构提高强度，保证压力装置的结构强度［9］。

压力筒的应力应变分析结果，如图3所示。

图3 压力装置的应力和应变图Fig.3 Stress and Strain Diagram of the Pressure Device

根据图3分析结果，压力装置的最大应力值为336.39Mpa，最大应变为0.001682mm，最大应力的计算结果小于结构钢的强度极限值，因此，尺寸设计符合要求。

3 装置密封设计

为了能确保压力可以达到预计的80Mpa，压力容器的密封的设计尤为重要，它的设计直接影响到整个压力容器的压力值的大小。本试验装置采用有“密封之王”美誉的O形橡胶圈密封［10］。采用非线性有限元分析软件MARC对密封结构进行建模，进而分析和计算不同的结构参数对密封性能的影响，从而选择合适的参数进行优化，得到最优解。

3.1 O形圈结构参数设计

O形圈安装在沟槽和被密封面之间，截面受压缩变形使密封圈对接触面即密封面力的作用即产生反弹力，形成初始密封。

当处于预紧密封状态的O形圈受流体压力作用时，会被挤压到沟槽的一侧。流体压力越大，O形橡胶圈给密封面的压力越大，形成的自紧密封就越大。结构示意图，如图4所示。自紧密封程度取决于压缩变形量，压缩变形量则用压缩率ε来表示：

图4 结构示意图Fig.4 Structure Diagram

式中：d2—密封截面的直径；H0—密封沟槽底面距密封面的高度。形成自紧密封要满足：

式中：Kc—压力传递系数；σmax—最大密封接触压力；σ1max—最大初始接触压力；p—工作压力。

O形圈的密封圈模型的结构参数，如图5所示。

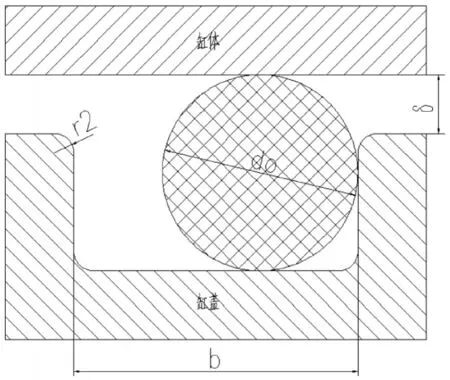
图5 O形橡胶密封圈模型结构参数Fig.5 O-shaped Rubber Seal Model Structure Parameter

3.2 MARC有限元分析

采用的O形橡胶圈为美国PARKER公司的产品，硬度为IRHD（国际橡胶硬度等级）85，为简化计算，模型采用2D平面建模。取O形圈为研究对象。由于载荷和结构的轴对称性，因而在建立有限元网络模型的时候，O形圈的压缩率为15%。将密封圈的二维图导入Marc Mentat 2010里，橡胶圆周长为18.84mm，间隙为0.1mm，网格划分应小于0.1mm，所以在橡胶圈外圆周2等分种子点，自动划分网格，网格划分结果，如图6（a）所示。

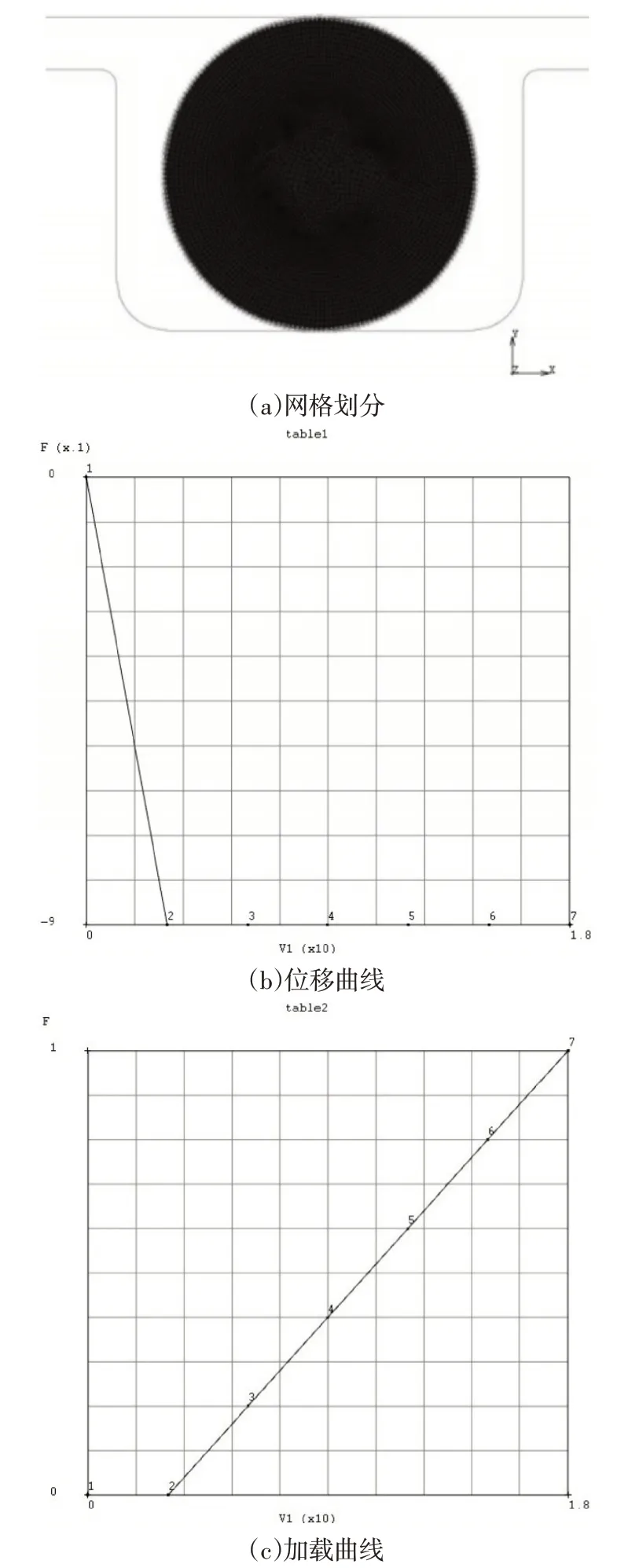
图6 网格划分和参数设置Fig.6 Meshing and Parameter Setting

用图6（b）位移曲线控制。在边界条件的设置中，在橡胶圈的受压侧加载80Mpa，用图6（c）加载曲线控制加载情况。

在载荷步的定义中，定义总加载时间为18s，总子步数为180，收敛容差为0.2。密封圈采用四边形单元quad11，采用Mooney-Rivlin模型分析和计算橡胶材料的力学性能，橡胶的硬度为85，利用公式算得Rivlin的系数C10和C01，分别为1.87和0.47，体积模量VALUE为23400。

3.3 计算结果分析

运行软件得等效应力和接触压力，如图7（a）和图7（b）所示。沿主密封面的接触压力曲线，如图7（c）所示。

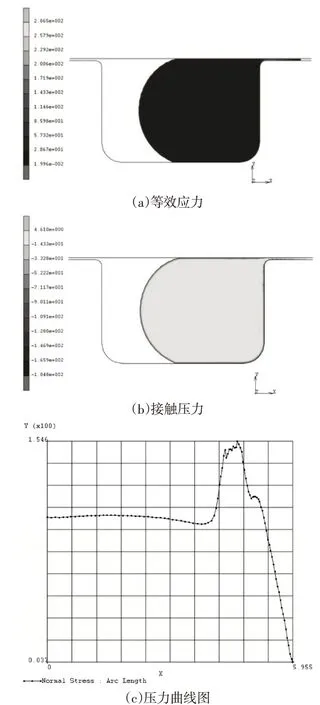
图7 分析结果Fig.7 Analysis Result

从图中得知，橡胶圈在80Mpa内压力作用下，部分被挤入间隙中。分析结果最大等效应力为286.5Mpa，最大接触压应力154.6Mpa＞100Mpa，由于O形密封圈密封的必要条件是密封界面上的最大接触压应力σmax不小于工作内压p，即本密封满足自紧密封。

下面研究6mm直径的O型密封圈的密封间隙对于最大接触压应力和Von Mises应力的影响。槽深的数据，如表1所示。

表1 槽深的数据Tab.1 Data of Groove Depth

研究不同密封间隙下，80Mpa油压作用，密封圈的接触压应力和Von Mises应力的大小。根据有限元的分析，不同密封间隙的最大接触压应力和Von Misess应力的结果，如图8所示。

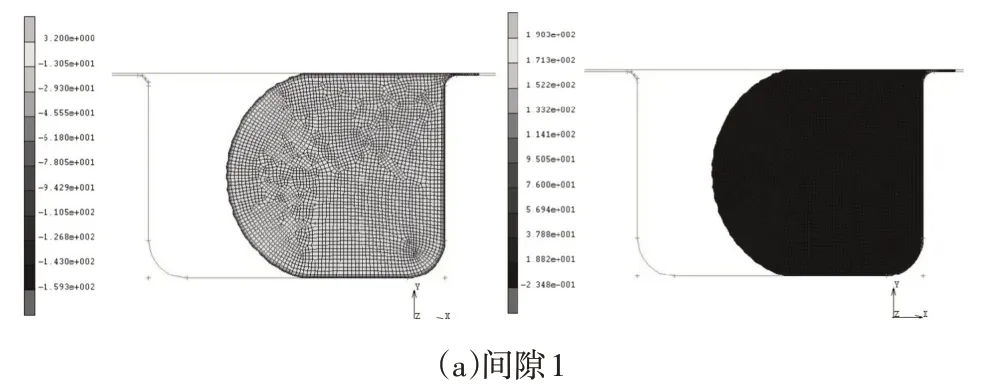
图8 不同密封间隙分析结果Fig.8 Different Sealing Gap Analysis Result

根据公差的大小来选定密封间隙的范围，H7的公差的密封间隙为0.043mm-0.146mm选取三个间隙进行分析。根据Marc非线性有限元分析结果显示，随着密封间隙的增大，最大接触压应力在减小，Von Mises应力在增大。一般来讲，应力值越大的区域，材料越容易产生裂纹。

再分析压缩变形量对最大接触压应力和Von Mises应力的影响根据有限元的分结果，如图9所示。

图9 不同压缩率分析结果Fig.9 Different Compression Rate Analysis Result

根据Marc非线性有限元分析得，随着压缩率的增加，最大接触压应力的变化规律呈现先减小后增大的趋势，而最大Von Mises应力呈现的是先增大后减小的趋势。为了尽可能减少最大Von Mises和增大最大接触压应力的值，应该选取较小的密封间隙和压缩率。

结果显示最大接触压应力都大于80Mpa，符合自紧密封条件，为了寻找密封尺寸规律，统计不同密封间隙和不同压缩率条件下其最大接触压力和最大Von Mises应力的具体数值结果，如表2所示。

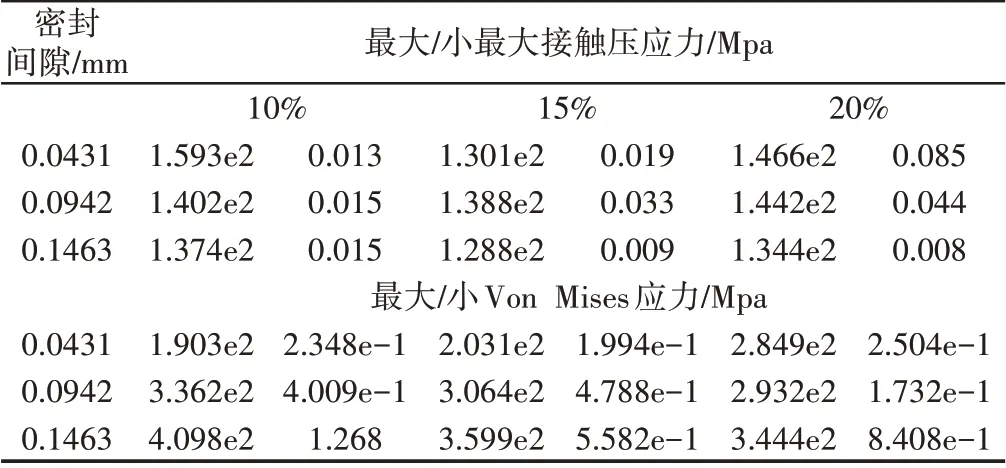
表2 不同参数分析结果Tab.2 Analysis Result of Different Parameter

运用Matlab软件得出图10所示曲线，从曲线中可看出不同压缩率的曲线趋势大致相同，密封间隙为0.043mm，压缩率为10%的Von Mises最小。

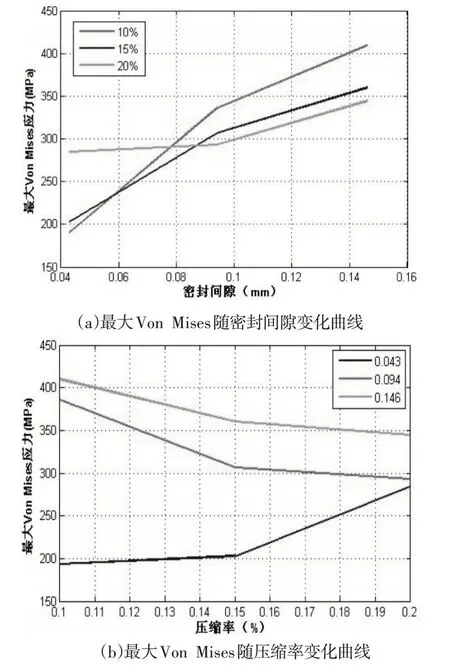
图10 参数变化曲线Fig.10 Parameter Variation Curve

由图可知，密封间隙在公差范围0.043mm-0.146mm之间，压缩率在10%-20%之间，最大接触压应力超过80Mpa，满足自紧密封条件；随着密封间隙的增大，接触压应力呈现减小的趋势，最大Von Mises应力趋势相反；随着压缩率的增加，最大接触压应力先减小后增大，Von Mises应力是先增大后减小，说明80Mpa下，小的密封间隙和压缩率对于较小接触压应力和最大Von Mises应力具有积极的作用，可作为设计超高压压力容器的O形圈的密封尺寸设计提供参考依据；使用非线性有限元分析软件MARC进行优化，O形橡胶圈都有不同程度挤入间隙内。优化结果是：密封间隙为0.043mm，槽深为5.357mm，压缩率为10%的O形圈密封结构。

4 试验分析

根据设计尺寸，采用筒状结构，对耐高压观察试验装置进行加工，为压力装置的装配图，如图11所示。

图11 试验装置Fig.11 Test Device

试验过程中，压力由0MPa加载到80MPa，取3次加载过程的观察窗低压面中心点的轴向位移，将试验拟合值与理论值、有限元分析结果进行对比，如图12所示。

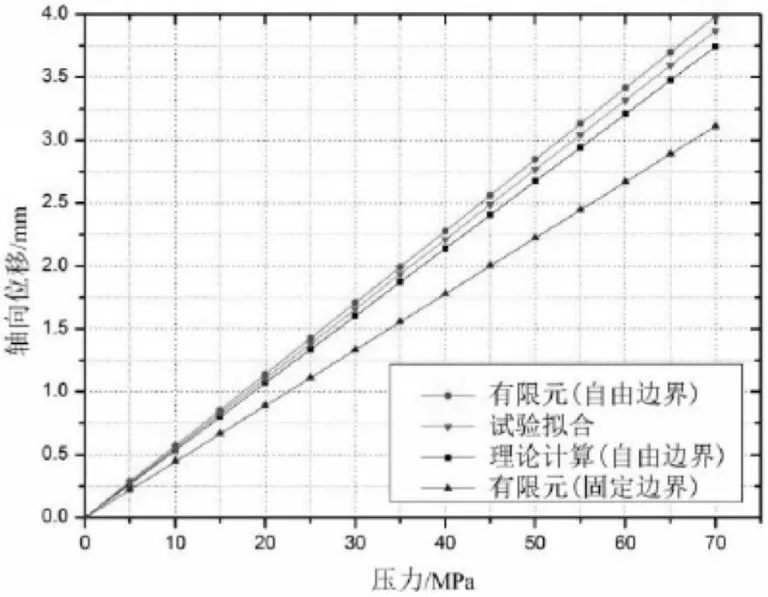
图12 轴向位移对比分析Fig.12 Comparative Analysis of Axial Displacement

由图可知，实际轴向位移与自由边界的理论值基本一致，表明装置设计合理，由于观察窗采用有机玻璃材料，存在一定的蠕变变形，造成试验值略大于理论值。

5 结论

针对耐高压试验观察装置结构和尺寸等进行设计，并采用试验方法对装置可靠性进行分析，结果可知：

（1）用数值的方法计算压力装置的内径、壁厚等基本的尺寸，再建立相应的三维立体模型，通过有限元分析的方法对三维模型进行有限元分析，以验证压力装置尺寸的合理性，最后的计算结果符合强度要求；

（2）试验装置采用O型圈结构，密封间隙在公差范围0.043mm-0.146mm之间，压缩率在10%-20%范围内，利用Marc软件对O型圈进行密封分析，得出较为合适的密封间隙和压缩率，分别为0.043mm和10%，并得到了80Mpa下O型圈随着密封间隙和压缩率的变化其最大接触压应力和最大Von Mises应力的变化趋势，对今后选择合适的密封间隙和压缩率有一定的指导意义；

（3）采用试验、理论分析及有限元仿真对比分析观察窗主轴位移，结果表明理论分析和试验结果基本一致，表明装置设计合理，可以作为试验分析的依据。