自控网络Petri模型下机器人装配线多目标平衡1

郭艳红，李建伟

（1.山西传媒学院，山西 晋中030619；2.太原科技大学计算机学院，山西 太原030024）

1 引言

装配线是在汽车和消费电子行业中非常重要的以流程为导向的系统。近年来，机器人已被广泛应用于这些类型的系统中［1］。机器人装配线的有效利用演变为解决机器人装配线平衡问题的需要，装配线平衡研究难点在于满足生产节拍、作业顺序等约束下，组合并优化分配作业单元，避免资源浪费，提高生产效率。针对装配线平衡问题，相关领域学者进行了研究，刘雪梅等［2］基于工位复杂性测度的随机型装配线平衡优化，运用数学模型方法建立工位平衡规划模型，并进行编程求解；文献［3］考虑了工序间的优先关系约束和节拍约束，将工序和机器分配到工位中，应用混合灰狼算法来解决装配线平衡问题；文献［4］提出考虑能效的多机器人协同装配线平衡方法，以能源消耗、机器人总投入成本最小化为目标，采用延迟爬山算法提高机器人搜索性能，经验证该方法有效。

本研究借鉴既往研究经验，利用自控网络的智能性自动求取机器人装配生产线多目标平衡问题最优解。最后为测试自控网络的应用效果，进行实证分析。结果表明：自控网络应用下，机器人在设定的约束条件下，装配节拍缩短、平滑系数降低，装配平衡率提高，实现多目标平衡的目的。

2 利用自控网络Petri模型优化机器人装配多目标平衡问题

装配平衡旨在实现目标最优化，以达到某种目的，如成本最低、资源消耗最少、时间最短等等［5］。为此，利用自控网络求解机器人装配生产线多目标平衡问题最优解。

2.1 自控网络Petri模型

Petri模型是自控网络系统的抽象［6］。为了方便研究机器人装配生产线多目标平衡问题，首先根据自控网络系统建立形式化模型，以明确机器人的装配过程，为后续建立目标函数方程奠定基础。

2.1.1 自控网络基本Petri模型

自控网络Petri模型主要由四个基本目标组成，如表1所示。

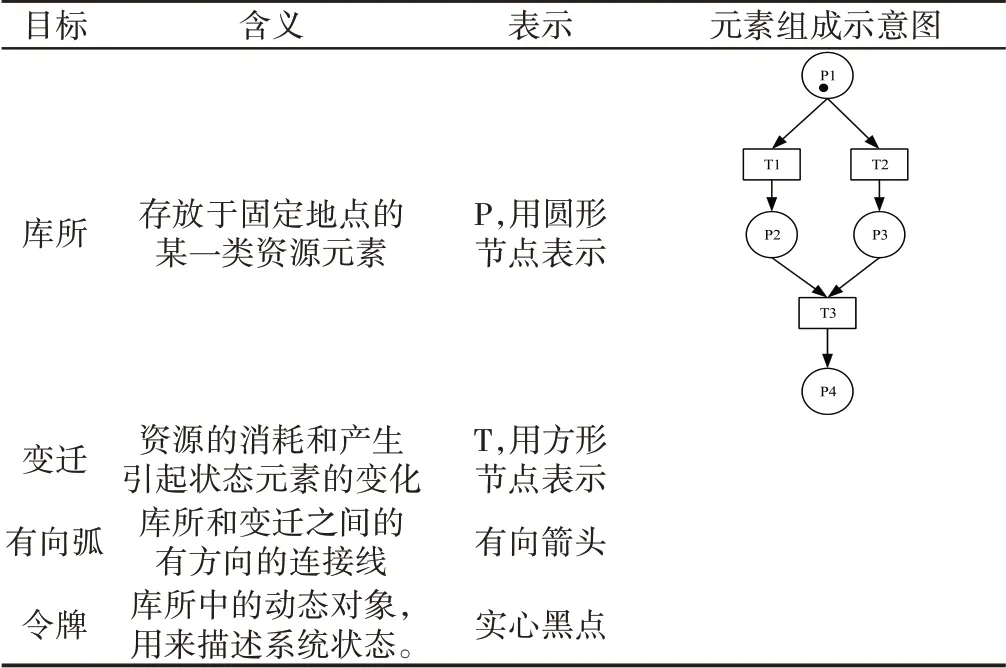
表1 自控网络Petri模型基本组成目标Tab.1 The Basic Composition Goal of Automatic Control Network Petri Model

2.1.2 自控网络Petri模型建模方法

自控网络Petri模型建模主要有三种，自上而下法、自下而上法、二者混合法，如表2所示。

表2 自控网络Petri模型建模方法Tab.2 Modeling Method of Automatic Control Network Petri Model

基于混合法的优点，采用该方法建立自控网络Petri模型分析这些模块的运行机制，建立宏观模型［7］。具体过程如下：

步骤1：确定机器人装配生产线自控网络建模总目标；步骤2：针对机器人装配生产线环境中自控网络的应用特点，将其划分为多个子模块，每个子模块相当于一个中层局部模型。这些子模块既相互独立又相互联系；步骤3：分析每个子模块的内部运行机制和特征，并再次进行分解，得到若干个底层对象，最后以此建立Petri网模型。步骤4：综合步骤2和步骤3，建立顶层模型。步骤5：将模型的每个对象被看作是一个封装起来的库所，给出工艺流程图；步骤6：为判断自控网络Petri模型的正确性以及是否符合实际装配线系统，利用关联矩阵法对其进行分析；步骤7：检验第6步的分析结果，若存在问题则返回第2步进行逐层检查。

2.2 建立自控网络多目标控制方程

2.2.1 基本假设

假设1：各个装配环节的作业是明确的；假设2：装配环节之间的逻辑顺序是已知的；假设3：不同产品的同一作业要素只能分配到同一个工作站；假设4：装配生产的总时间确定。假设5：每个工作站只有一个机器人；假设6：单个作业要素的时间均小于理论节拍；假设7：装配生产线上不存在并行工作站的情况；假设8：每个机器人的技术水平相同，能够胜任任意一项工作；假设9：生产线上同时装配的产品结构和工艺相似［8］。

2.2.2 自控网络控制方程

自控网络在机器人装配生产线多目标平衡中应用的目的是期望通过协调控制多个装配流程，以提高产品生产效率和生产质量［9］。为实现上述目的，建立多目标函数方程，具体如公式（1）所示。

式中：minT的目标是实现生产节拍最小化；minB的目标是实现装配成本最小化；minC的目标是实现装配线上各工作站的工作负荷最小化。方程中其余参数和变量表示，如表3所示。

表3 方程关联参数和变量表示Tab.3 Expression of Related Parameters and Variables of Equations

2.2.3 约束条件

上述建立的多目标函数方程需要在一定的约束条件下才能求出最大值或最小值，设置自控网络控制方程约束条件。具体有五个：

（1）约束条件一：每个项任务均被分配到同一个工作站，其表达式为：

（2）约束条件二：遵循装配生产线任务的优先次序。其表达式为：

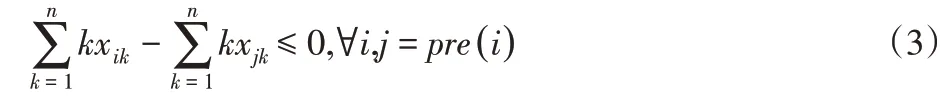
式中：pre(i)按照作业任务的优先关系，先于作业任务i完成的作业任务集合。

（3）约束条件三：生产线上的机器人至多可以划分到一个工作站。其表达式为：

（4）约束条件四：每个工作点被分配到产品的加权作业所需时间，保持在装配生产线的理论周期。其表达式为：

式中：R—装配线的理论节拍。

（5）约束条件五：任务分配和机器人分配的决策变量都是0/1型变量。其表达式为：

至此，完成自控网络多目标函数方程约束条件的建立，是实现装配生产线多目标平衡的重要步骤。

2.3 自控网络控制方程求解

建立自控网络控制方程后，求解在上述五种条件约束下装配生产线多目标平衡的最优解。由于建立的自控网络控制方程的三个目标之间具有一定的制约关系，选取粒子群算法进行求解，加入遗传算法改进基本粒子群算法，利用遗传算法的自然选择机制提高算法的搜索性能。算法基本流程，如图1所示。

图1 算法基本流程Fig.1 Basic Flow of Algorithm

步骤1：输入作业数目、作业时间以及作业优先关系矩阵等相关参数。步骤2：初始化粒子群粒子的速度和位置；步骤3：利用遗传算法的编码方法对粒子进行编码；步骤4：计算每个粒子的适应值；步骤5：更新粒子速度和位置；步骤6：排序整个粒子群的适应值。将前一半粒子速度和位置代替后一半较差的粒子，保持pbest（每个粒子根据自身找到的最好位置）和gbest（群体找到的最好位置）不变。步骤7：对邻域进行搜索，设搜索次数为k，当前解为s，邻域为s′，若s′优于s，则k不变；否则k=k+1，直至k=5。步骤8：判断是否满足迭代终止条件。若满足，则输出解，否则回到步骤3。

3 仿真实验与分析

为验证自控网络在机器人装配生产线多目标平衡中的应用效果，实验操作系统为Windows 10，CPU型号为Core i5-661，主频3.33GHz，运行内存为8G。在MATLAB（R2018a）软件中进行编程与仿真。

3.1 参数设置

表4 参数设置Tab.4 Parameter Setting

3.2 机器人装配线建模

以某汽车企业座椅装配生产线为例探究多目标平衡问题。该企业座椅机器人装配线建模，如图2所示。

图2 汽车座椅机器人装配线模型局部Fig.2 Part of Assembly Line Model of Automobile Seat Robot

在该装配生产线上，共有18个作业任务，8个工作站，8个装配机器人、5个产品类型。

3.3 建立自控网络Petri模型

利用正文章节（一）中自控网络Petri模型建立流程建立汽车企业座椅装配线Petri模型，如图3所示。

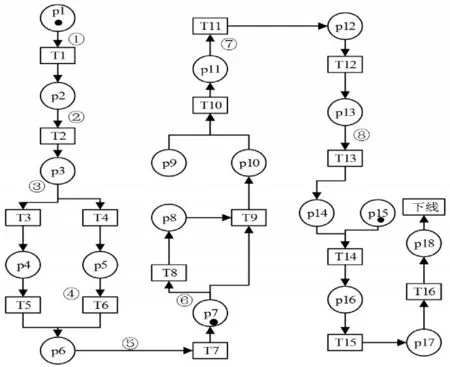
图3 座椅装配生产线Petri模型Fig.3 Petri Model of Seat Assembly Line

图3中，p1～p18个库所变迁过程代表18个作业任务，分别在装配线上分别有①～⑧个工作站，配置8个装配机器人，其作业任务分别为滑轨总成装配、坐垫总成装配、靠背总成装配、护板安全带锁扣装配、头枕装配、线束整理、外观功能检测及包装。

3.4 评价指标

（1）生产节拍C：是指连续生产相邻两个产品至生产完成所需要的时间间隔。间隔越小，生产节拍越好，装配生产能力越好。（2）平滑系数SI：是衡量装配线上工作站负荷是否均衡的指标，其计算公式为：

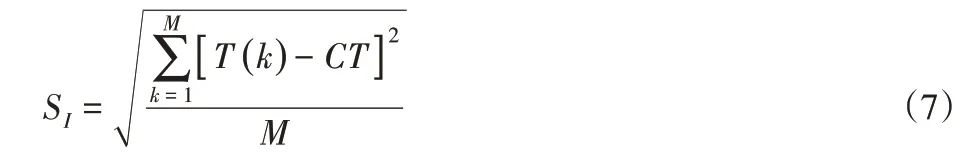
式中：T(k)—第k个工作站时间。平滑系数SI越小，工作站之间负荷越均衡。（3）装配线平衡率BP—反映装配线平衡效果的指标，其计算公式为：

式中：T—总作业时间，M—工作站总数，CT—节拍。装配平衡率BP越大多目标均衡效果越好。

3.5 结果分析

利用所提自控网络方法、文献［2］（基于工位复杂性测度的随机型装配线平衡优化）、文献［3］（基于混合灰狼算法实现第Ⅱ类机器人U型装配线能耗优化）、文献［4］（考虑能效的多机器人协同装配线平衡方法）方法求解机器人装配生产线多目标平衡的性能。实验1为生产节拍对比，基于上述实验环境，测试四种方法生产18个作业任务之间的生产节拍。利用仿真平台计算时间，共计9组数据，具体实验数据，如图4所示。

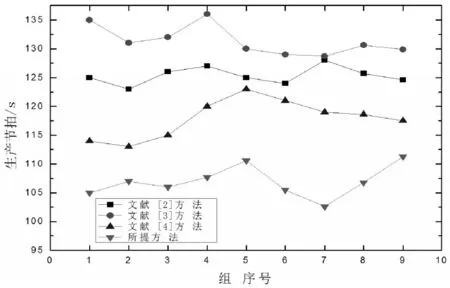
图4 生产节拍对比Fig.4 Comparison of Production Rhythm

由图4可知，在相同实验条件下，所提方法与文献［2］/［3］/［4］三种方法相比，生产节拍较低，最低用时为102.6s。因为所提方法在自控网络方程的构建中考虑了生产节拍最小化要素，并遵循装配生产线任务的优先次序的约束条件，缩短了生产节拍。

实验2为平滑系数对比，验证不同工作站下四种方法的平滑系数趋势，具体实验结果，如图5所示。

由图5可知，所提方法平滑系数低于对比的三种方法，且波动幅度较小，最低平滑系数为5.05，说明运用该方法后各工作站之间负荷较均衡，可以较好地疏通工作站之间的空闲及堵塞。实验3为装配线平衡率对比，也是评价装配线平衡效果的重要指标，利用仿真平台记录不同方法的装配平衡率，具体结果，如表5所示。

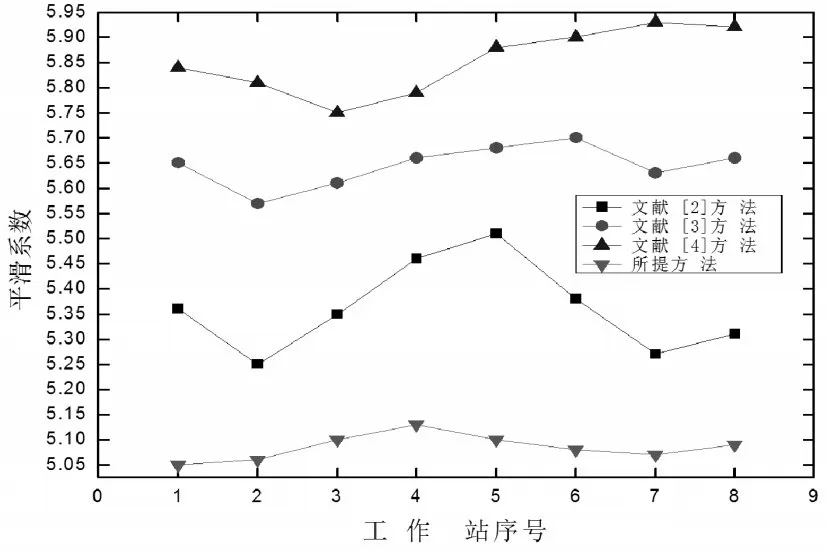
图5 平滑系数对比Fig.5 Comparison of Smoothing Coefficients

表5 装配平衡率对比Tab.5 Comparison of Assembly Balance Rate 单位：%

由表5可知，在不同装配站数量下，对比其他三种方法所提方法的平衡率较高，最高装配线平衡率为95.62%。因为所提方法对自控网络控制方程设置了不同的约束条件，完善了装配生产线的难点问题，提高了生产线多目标平衡。证明自控网络在机器人装配生产线多目标平衡中具有较好的应用效果。

4 结束语

保证机器人装配线多目标平衡是现今研究的重点内容，为此，进行自控网络在机器人装配线多目标平衡中的应用研究。通过建立自控模型，求解模型最优解，完成平衡问题的探讨。通过验证分析，证明了自控网络的应用效果。本研究只针对直线型、单一品种的装配线平衡问题，在今后的研究中需要进行扩展，探讨更多类型装配线的平衡问题。