均匀分布与反馈补偿优化脉冲噪声抑制

刘 岩，王 月

（1.国网冀北电力有限公司营销服务中心（计量中心），北京102208；2.辽宁对外经贸学院,辽宁 大连063210）

1 引言

电力线通信能够依托现有电力网络实现信息传输，具有成本低廉、连接方便等优点，在智能电网、智能家居等领域有着十分广泛的应用［1］。但是，电力线网络并不是专用通信网络，用于信息传输存在信道损耗大、多径效应严重以及噪声干扰强等问题。为克服这些缺陷，电力线通信系统采用能够适应多载波通信的正交频分复用（OFDM）。然而，与大多数通信系统不同的事，电力线通信中的噪声不能直接建模为加性高斯白噪声［2，3］。脉冲噪声通常是由于电力网络中各种设备瞬时开关引起的会导致OFDM通信出现突发性比特错误，抑制噪声脉冲是电力线通信系统研究的热点问题［4］。

目前，抑制脉冲噪声的方法主要包括非线性处理法［5］、迭代消除法［6］、压缩感知法［7］等。为了抑制电力线通信脉冲噪声，研究人员提出了多种抑制方法，文献［8］提出基于接收信号峰值估计脉冲频率，建立峰值频谱与脉冲特征之间的关系，据此实现峰值消引脉冲噪声抑制，可用于未知噪声条件下电力线通信噪声抑制；文献［9］针对非线性脉冲噪声抑制方法存在非线性失真，提出基于脉冲噪声重构与迭代的非线性失真补偿方法，降低了电力线通信误比特率，但该方法对重度脉冲噪声抑制性能不佳。

针对上述问题，文中提出了一种用于电力线通信系统脉冲噪声抑制的改进方法。算法在发射端将传统瑞利分布信号峰值转换为均匀分布，降低发射信号PAPR；然后，对非线性置零操作后的信号，设计了基于反馈补偿的脉冲噪声再抑制方法；最后，利用频域重构补偿脉冲噪声抑制过程中的非线性失真，仿真实验验证了所提改进方法对电力线通信系统脉冲噪声抑制的有效性。

2 系统模型

电力线通信发射端的信号可以表示为：

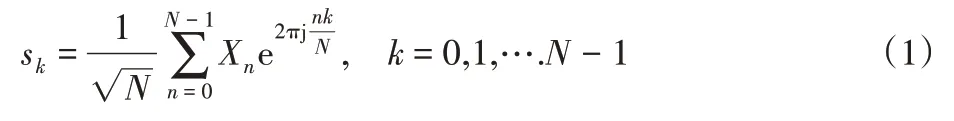
式中：n、k—信号的时域和频域采样，Xn—经过编码、交织和星座映射后的基带调制符号，基带调制符号是由发送符号经过编码、交织与星座映射得到的，满足共轭对称性，N—离散点数，则OFDM信号幅度为：

式中：sr、si—信号的虚部与实部。根据中心极限定理，sr和si均为独立同分布的高斯分布变量，因此信号峰值幅度服从瑞利分布，其概率密度函数（pdf）为：

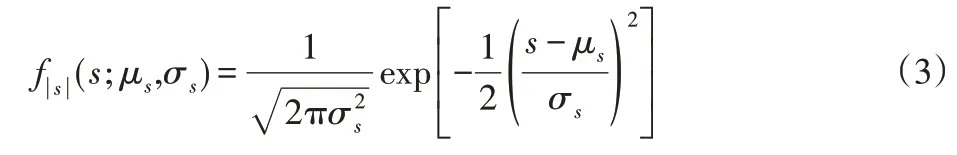
式中：μs、σs—信号包络的均值和标准差，P=‖As‖∞各OFDM信号子载波的峰值幅度，‖· ‖∞—无穷范数。

脉冲噪声严重影响了电力线通信性能，为有效抑制脉冲噪声，研究人员提出了多种电力线通信脉冲噪声模型［10］，文中应用伯努利高斯过程描述电力线通信脉冲噪声。该模型基于高斯过程表征脉冲噪声的幅度特性，即zi,k=bk,nw,k，式中nw,k为零均值高斯白噪声，k=0,1,…,N-1，bk为独立同分布的伯努利随机过程，其概率密度函数可表示为：

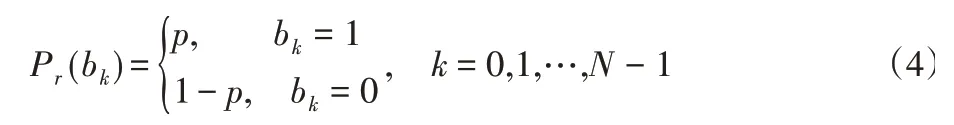
式中：p—电力线通信过程中脉冲噪声出现的概率。实际电力线通信过程中，某一时间段的总噪声概率密度为：

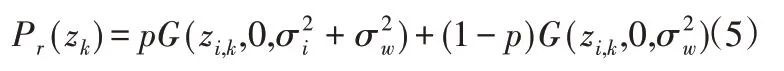
式中：σw、σi—背景噪声和脉冲噪声幅度的标准差。

目前，电力线通信常用的脉冲噪声抑制方法为非线性抑制方法，但其存在以下问题：（1）OFDM子载波数量较多的宽带通信信号的峰值平均功率比（PAPR）增加，降低了置零方法的脉冲噪声抑制性能；（2）非线性方法对重度脉冲噪声污染信号抑制能力有限；（3）非线性方法会引起较为严重的失真，影响信号解调性能。为此，文中提出一种改进的电力线通信系统脉冲噪声抑制方法。

3 改进脉冲噪声抑制方法

3.1 基于均匀分布优化发射信号

文中将信号峰值的瑞利分布转换为均匀分布，实现降低信号的PARP，优化过程为：

式中：sgn(x)=x/||x—信号的相位，F||s(s)—传统瑞利分布信号幅度的累积密度函数（CDF），—累积密度函数逆变换。根据式（6），OFDM信号峰值由瑞利分布转换为均匀分布。CDF和PDF之间存在积分与导数关系，因此OFDM信号的幅度可以表示为：

瑞利分布转化为均匀分布的过程扩展了低功率信号的幅度，压缩了高功率信号的幅度，但随着m的增加，指数转换方法的低功率信号振幅的提升会随之减小，影响转换后信号的均匀度。为此，采用基于艾里函数的转换方法：

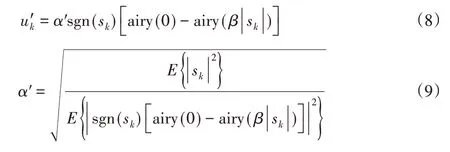
式中：airy(·)—艾里函数，将OFDM幅度转化为均匀分布能够显著降低信号峰值功率，进而降低PAPR，优化后OFDM信号的PAPR为：

从生成OFDM信号中选择PARP最小的信号进行传输，信号子载波个数不同对PARP降低的程度也不同，为此采用互补CDF（CCDF）来评估信号PAPR的降低程度。

3.2 基于反馈补偿的脉冲噪声再抑制

对于受到重度脉冲噪声污染的电力线通信信号，经过置零操作对脉冲噪声进行初步抑制后，仍然会有大量的脉冲噪声残留在剩余信号中，从面影响后续进行的通信信号OFDM解调性能。为此，在已有研究基础上，提出了基于反馈补偿的脉冲噪声再抑制方法，以对剩余信号中的重度脉冲噪声进行再抵制，其实现流程如图1所示，图中，z^k和Z^k分别为对傅立叶变换后电力线通信信号叠加的反馈补偿信号及其傅立叶变换信号。

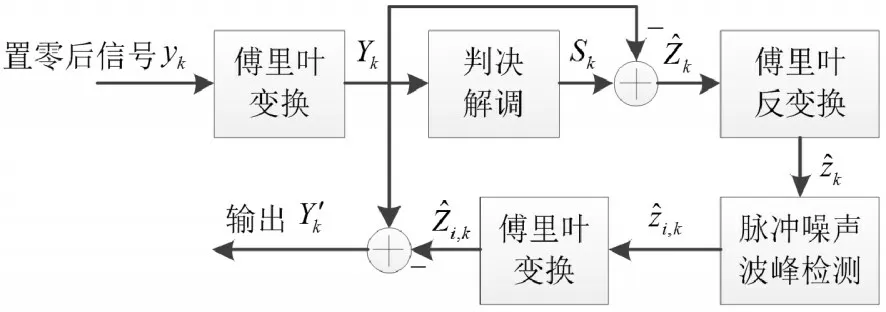
图1 反馈补偿脉冲噪声再抑制流程Fig.1 Feedback Compensation Impulse Noise Suppression Process

首先，计算置零操作输出信号的傅里叶变换，将其变换到频域，为简化过程，假设信道为均衡信道，将变换后的频域信号输入到判决解调模块中，按照发射端调制方式在频域进行解调操作，获得解调后频域信号此时，背景噪声和脉冲噪声之和的估计值进行逆傅里叶变换，得出噪声之和的时域估计结果z^k。

噪声之和的平均功率可以表示为：

由和式（11）所示平均功率，可以实现脉冲噪声的波峰检测，即：

式中：η—噪声脉冲波峰检测门限系数。

4 仿真实例分析

以电力线通信模型构建仿真链路测试文中改进方法性能。仿真链路中，电力线通信编码方式采用1/2卷积码，信号调制方式为8PSK，信号采样频率为25MHz，数据块长度为1024，子载波个数为511，背景噪声模型采用高斯白噪声，脉冲噪声模型采用伯努利高斯过程。

采用COB门限和DPTE门限进行对比测试。采用均匀分布优化，两种门限对电力线通信系统脉冲噪声的抑制性能仿真结果如图2所示，脉冲噪声概率p=0.1。

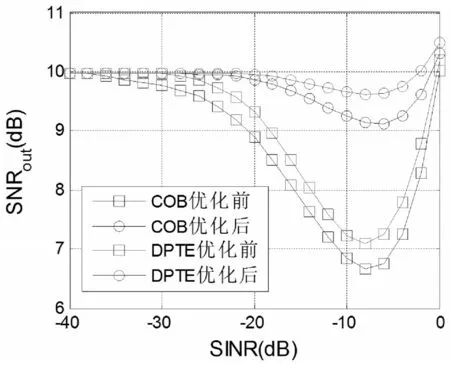
图2 均匀分布优化性能Fig.2 Uniform Distribution to Optimize Performance

仿真结果表明，采用均匀分布优化发射信号后，基于两种门限的置零方法对系统脉冲噪声的抑制能力均得到了增强。SINR为-20dB时，对于COB门限置零方法，均匀分布优化前，输出信噪比约为8.9dB，优化后输出信噪比约为9.8dB，提升了约0.9dB；对于DPTE门限置零方法，优化前输出信噪比约为9.3dB，优化后输出信噪比约为9.9dB，提升了约0.6dB。这是因为在发射端将传统瑞利分布转化为均匀分布后，能够有效降低信号PAPR，增加将OFDM峰值信号从接收信号中识别出来的概率，信噪比的提升间接地提高了脉冲噪声抑制能力。

为进一步测试文中算法（记为INMUDFCFR）的性能，将其与频域峰值估计脉冲噪声抑制方法［8］和基于改进置零门限的脉冲噪声抑制方法［10］在同等条件下进行仿真实验，统计电力线通信系统误比特率作为评价指标，脉冲噪声概率p=0.25，即重度脉冲噪声污染，实验结果如图3所示。

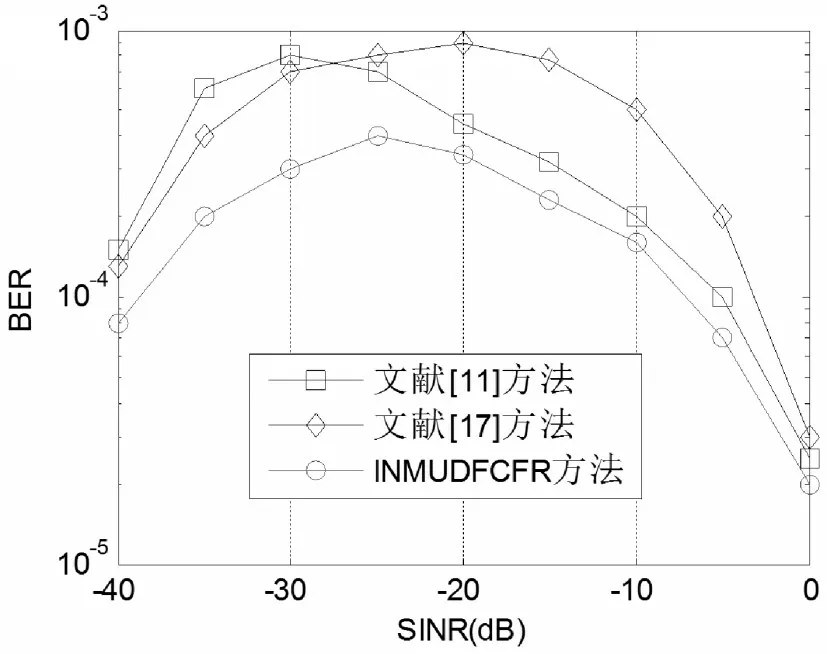
图3 算法性能对比结果Fig.3 Performance Comparison Results of Different Algorithms

仿真实验结果表明，对于重度污染信号，随着SINR的增加，三种脉冲噪声抑制算法的误比特率呈现出先上升后下降的趋势，文中提出的INMUDFCFR算法对电力线通信系统脉冲噪声抑制性能更优，这是因为该算法将传统瑞利分布峰值幅度转换为均匀分布，有效降低了信号PAPR，采用反馈补偿进一步抑制置零操作后的残留脉冲噪声，并利用频域重构对脉冲噪声抑制产生的非线性失真进行补偿，能够在有效抑制系统脉冲噪声的同时降低误比特率，仿真实验结果验证了理论分析的正确性。

5 结束语

针对电力线通信系统脉冲噪声抑制问题开展了研究，提出了一种基于均匀分布优化和反馈补偿的电力线脉冲噪声抑制算法。该算法首先将发射信号的瑞利分布进行分析，并将其峰值转换为均匀分布峰值，以降低信号的峰值平均功率比（PAPR），然后针对非线性置零信号设计了一种基于反馈补偿网络的重度脉冲噪声再抑制方法，进一步提高算法对脉冲噪声的抗干扰能力，最后，通过频域重构补偿过程对算法在噪声抑制过程中引起的非线性失真进行补偿，以保持原信号特征。仿真实验结果表明，算法能够有效抑制电力线通信中的重度脉冲噪声，降低了电力线通信误比特率，从而验证了算法的有效性。