散热器自动穿管机构定位误差预测
2021-09-23郑永樑
郑永樑,张 斌,夏 鑫
(1.贵州大学机械工程学院,贵州 贵阳550025;2.贵航工业贵州永红航空机械有限公司,贵州 贵阳550025)
1 引言
散热器在生产过程中其穿管的方法与手段会影响散热器总成的质量和产量,目前国内散热器制造中穿管工序仍需人工完成,工人劳动强度大,穿管的精度和效率低,成品一致性差,已成为国内企业散热器制造的技术瓶颈。因此需要开发出可实现散热器自动穿管的机构,提高企业生产效率和产品质量。
管导向升降部件通过气缸作用实现垂直运动,但由于滚珠丝杠综合误差的存在以及气缸作用在运动件时,出现爬行等原因,导致穿管机构的精度难以保证,穿管机构的定位误差决定穿管工序质量,因此平台位置的定位误差预测是关键。平台定位误差确定已有许多学者研究:文献[1]对五轴数控机床建立三次样条插值的转角定位误差数学模型,并建立相应的误差实时补偿系统,结果显示模型拟合度高,可有效提高机床旋转轴转角定位精度。文献[2]运用激光干涉仪对重型数控机床的X轴的定位精度和重复定位进行了测量,达到预定的目标。但激光干涉仪测量设备安装复杂且成本高。文献[3]将机器视觉运用于重复定位精度测量上,测试方法简单,测量精度达到亚像素级,可用于微米级以下设备定位精度的测定,然而照明光源和分辨率会影响照片的质量,成本费用亦会增加。文献[4]分析了进给私伺服系统定位误差增长的原因,并基于BP神经网络建立工作台与螺母座间隙、滚珠丝杠倾斜度、工件负载与定位误差之间的映射模型,对定位误差进行预测。文献[5]等提出基于动态模糊神经网络,对数控机床时变定位误差补偿,结果表明该模型预测精度高,有良好的鲁棒性和泛化能力。但BP神经网络的误差按负梯度方向减少,过多的训练样本会使网络陷入局部收敛。文献[6]运用支持向量回归机建立精密数控平台X、Z轴的热误差模型,并依据支持向量回归机热误差模型的预测数据进行补偿实验,实验结果证明支持向量回归机建模方法具有较高的预测精度、泛化能力、补偿精度和鲁棒性。文献[7]基于支持向量机对镗孔加工为实验对象的加工系统误差模型,预测精度比RBF神经网络的要好。然而支持向量回归机的受惩罚因子和核函数参数的影响,容易陷入盲目搜索及“早熟”[8]。
穿管定位误差的快速预测是提高穿管效率和精度的基础,针对传统定误差度预测方法的弊端,利用支持向量回归机建立穿管机构定位误差预测模型,收集并训练穿管工序数据,预测定位误差,引入粒子群算法优化SVR的惩罚因子和核函数参数,提高预测准确度,为穿管的误差补偿提供依据。
2 自动穿管机构
自动穿管机构由穿管机构结构和散热器片夹紧工作台组成。穿管机构结构的主要功能是整齐容纳散热管,调节穿管升降部件和散热片夹紧工作台的高度,使散热管精确穿进散热片垄;散热器片夹紧工作台的作用是整理并夹紧散热片。
2.1 穿管机构结构
穿管机构结构主要由穿管机架、穿管导向升降部件和推管传动机架等组成,如图1所示。在气缸作用下穿管导向升降部件可在垂直方向运动,配合散热器片工作台的高度,伺服电机卷动推管从动带,继而带动管子推板,在管子推板的作用下,散热管沿着穿管导向板穿入夹紧的散热片。

图1 穿管机构结构Fig.1 Structure of The Tube-piercing Mechanism
2.2 散热片夹紧工作台
如图2所示,散热片夹紧工作台包括穿管工作台基础板,穿管工作台面板,散热片压紧板以及垂直和水平压紧散热片气缸等。零部件安装在穿管工作台基础板上,在垂直和水平压紧气缸作用下,散热片压紧板使在穿管工作台面板上的散热片固定压紧,散热管从穿管机构结构穿进散热片垄,完成穿管。

图2 散热器片夹紧工作台Fig.2 Heat Sink Clamping Table
2.3 自动穿管流程
送料机械手把散热管运送至穿管导向板,每根散热管头都有一根锥形头的穿管引导导向管,其作用是利于散热管穿入散热片,散热片上下有两排内孔。推管从动带带动管子推板,继而使散热管穿入散热片上排内孔,然后再进行散热片下排内孔的穿管,当穿管导向板中的传感器在穿管时的压力小于指定数值,则判断穿管成功,需进行2次穿管完成一个散热器芯穿管工序。完成穿管后散热器片夹紧工作台在滚珠螺杆作用下移动至压栅收口机构进行管子收口。
2.4 自动穿管机构定位误差影响因素
散热管和散热片属于小间隙配合,且散热片质地柔软,在穿管过程中,穿管机构的定位精度不满足要求,将会影响穿管工序质量。影响定位误差的因素有:
(1)气缸位移误差。为克服传统气缸定位精度不足的缺点,采用磁流变阻尼器的气动控制系统,通过改变电流大小,控制磁场强弱,改变气缸内的阻尼力,从而精确控制气缸位移。根据牛顿第二定律得到气缸的动力平衡方程:

式中:A—气缸腔活塞有效作用面积;P1—气缸1腔的压力;P2—气缸2腔的压力;Fz—外负载力;Ff—摩擦阻尼力;Fs—阻尼器产生的阻尼力;M—负载质量;y—活塞位移;y¨—活塞的加速度。其中Fs根据磁流变材料性能和控制磁阀路函数拟合以及Bingham本构关系[9],可由下式表示:
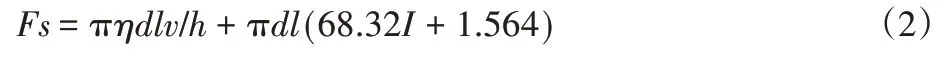
式中:d—主轴直径;I—电流;l—励磁线圈有效长度;η—磁流变液的粘度系数;h—主轴与阻尼器壳体内侧之间的间隙;v—主轴速度。式(2)中电流变化将影响气缸的作用力,进而导致气缸产生定位误差y,即:

而ΔI是电流扰动。
(2)丝杠变形。滚珠螺杆副在长时间运动后,摩擦产生的热量和环境温度的变化引起的热误差使丝杠副变形,将会影响散热器片压紧工作台的在水平位置的定位精度。
假设电机作用于丝杠的轴向力为F,则丝杠轴向力与擦力矩之间的关系可以下式表示:

丝杠发热量H:

式中:M—轴向摩擦力矩;F—丝杠受到的轴向力;n—参与接触的滚珠个数。
式(4)和(5)中,当电机施加给丝杠的轴向力不一样时,丝杠的轴向伸长量发生变化,且轴向力与轴向伸长量呈正相关,轴向力越大,产生的热量更多,进而使丝杠的变形量会更多,发热量H和环境温度K变化使丝杠的热变形量设为h,则:

电机转矩受电压U影响,且成正相关,可得:

(3)工作台与螺母座的间隙。穿管机构中滚珠丝杠与支撑轴间的间隙,连接部件的间隙以及联轴器间的间隙,会随着时间t推移变大,造成穿管机构连接部件的松动,影响定位精度,依据邓超[4]给出的间隙δ的指数函数表示关系为:

根据上述分析,穿管机构结构和散热片压紧工作台在X(散热器片压紧工作台水平运动方向)和Z(穿管导向升降部件垂直方向)方向的位置定位误差是难以确定的(Y是穿管方向),设定位误差为e=g(y,h,δ)。自动穿管设备运行一段时间后,工作台与螺母座的间隙变化小,且设备经过一段时间工作后进行维护,因此本文忽略间隙对穿管机构定位误差的影响,则e=g(y,h)。在穿管过程中,通过穿管导向板的传感器测出散热管受到的阻力在某个值范围之内,视为穿管成功,可建立散热管阻力T与穿管定位误差的关系,T↔e,T越大,则表示误差e也更大,则T=g(y,h)又结合式(3)和(7),得到新的映射关系:T=g(ΔI,U,K)。但由于T是复杂的非线性函数,难以通过精确建模得到准确的数值,而添加测量设备来测量误差会增加成本,因此可以把穿管机构定位误差视为“黑箱”,利用改进的支持向量回归机可以任意逼近复杂非线性函数及很好的泛化能力,建立穿管机构定位误差模型,通过上述推导,将自动穿管机构工作过程中的气缸输入电流I、滚珠丝杠电机的电压U和工作环境温度K作为输入,而输出则为穿管过程散热管受到的阻力T,预测穿管机构定位误差,为误差补偿提供依据。
3 支持向量回归机与粒子群算法
3.1 支持向量回归机(SVR)
设一个有n个样本的训练集为(Xi,yi),其中输入向量Xi∈Rn,输出yi∈R。样本可以通过高维特征空间中的线性函数进行拟合:

式中:φ(·)—非线性映射函数;ω—特征空间的权重向量;b—阈值。根据结构风险最小原理,综合考虑函数的复杂程度和误差值,支持向量回归可以如下表示:

式中:ζi,ζ*i—松弛变量;ε—误差。
引入拉格朗日乘子(αi,α*i),可将问题转化为:
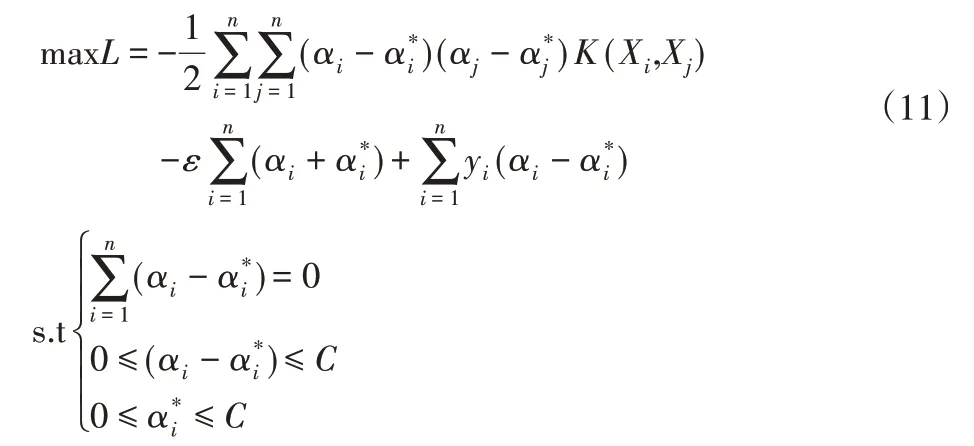
式中:K(Xi,Xj)=φ(Xi)φ(Xj)—核函数;C—惩罚因子。对上式进行求解可得SVR的预测模型:

SVR核函数有多种,本文选用径向基函数(RBF)作为核函数,即K(X,Xi)=exe(-‖X-Xi‖2/(2σ2)),其中σ是核函数的参数。SVR的模型准确度取决于核函数参数σ和惩罚因子C:过大的σ将会降低模型的准确度,但过小会造成拟合过度。而惩罚因子C则会影响模型的误差和复杂度[10]。因此,选择一种合适的方法来优化SVR参数σ和C对模型的建立至关重要。本文采用粒子群算法实现自动搜索得到SVR的最佳参数σ和C。
3.2 粒子群算法(PSO)优化支持向量回归机(SVR)
PSO是Eberhart和Kennedy在1995年提出的一种寻找连续非线性函数最优值的算法。粒子群算法初始化为一群粒子,每个具有d维空间的粒子有两个特征:位置和速度,即Xi={Xi1,Xi2,...,Xid}T和Vi={Vi1,Vi2,...,Vid}T。Pi={Pi1,Pi2,...,Pid}T是搜索空间内第i个粒子的最佳位置,而Pg={Pg1,Pg2,...,Pgd}T是全局最优位置。通过更新每个粒子的位置和速度,可以得到粒子个体极值Pib和粒子群全局极值Pgb。PSO可以根据以下方程进行迭代更新:
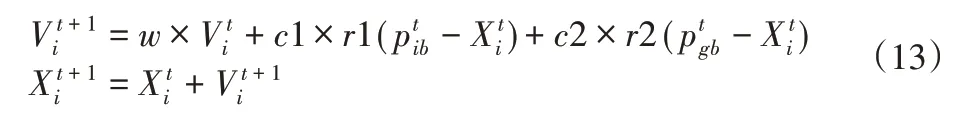
式中:t—迭代次数;c1,c2—搜索加速系数且都是正数;r1,r2—在(0,1)的随机数;w—惯性权重因子。
PSO优化SVR的流程图如图3所示:
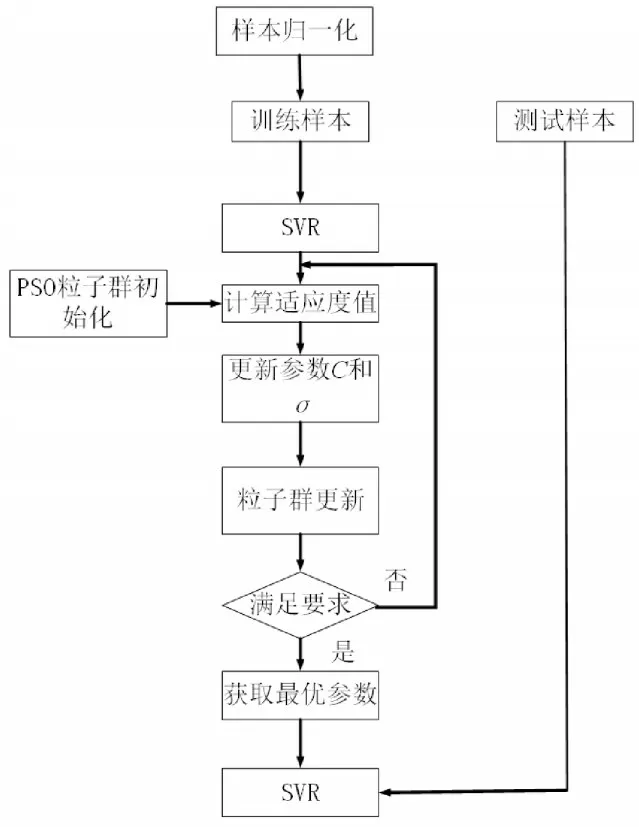
图3 PSO-SVR流程图Fig.3 The PSO-SVR Flowchart
(2)将归一化后的样本分为训练样本和测试样本。训练样本的作用是训练SVR模型,利用测试样本对建立的SVR模型进行测试。
(3)粒子群初始化。通过粒子群算法的更新和迭代,逐渐减小适应度值,达到目标要求后得到SVR模型的最优参数σ和C。
(4)得到的最优参数的SVR模型。
4 穿管机构定位误差预测
4.1 数据采集与PSO-SVR模型建立
在生产过程中获取穿管机构维护后初期(磨合磨损阶段),工作一段时间(稳定磨损阶段),及维护前(剧烈磨损阶段)的数据:气缸输入电流、丝杠电机电压,工作环境温度及穿管阻力,目的是让样本足够丰富。初始化粒子群参数,粒子数为30,迭代次数取100,其中c1=1.5,c2=1.7,w=1,而r1,r2是在(0,1)的随机数。
4.2 评价指标
通过计算平均相对误差(MRE),均方根误差(RMSE)及决定系数(R2)判断模型的优劣。
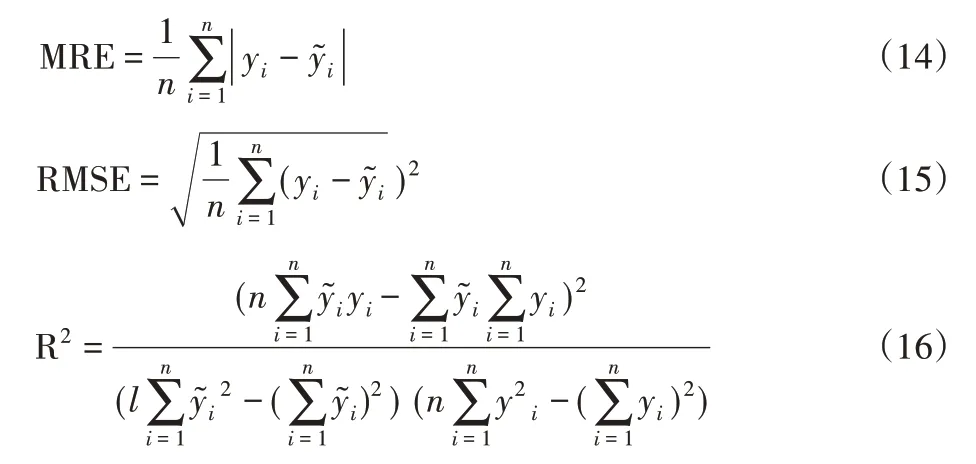
4.3 仿真分析
采集气缸气压、电机转矩、环境温度以及穿管最大阻力数据,将数据分为训练样本和测试样本,其中训练样本550组,测试样本50组,结果如下所示。
图4是粒子群算法对SVR惩罚因子C和核函数参数σ进行寻优,适应度值经过大约5代后逐渐收敛,得到最优参数C=24.9510,σ=2.2455。将优化后的C和σ代入SVR里,对测试样本进行预测。
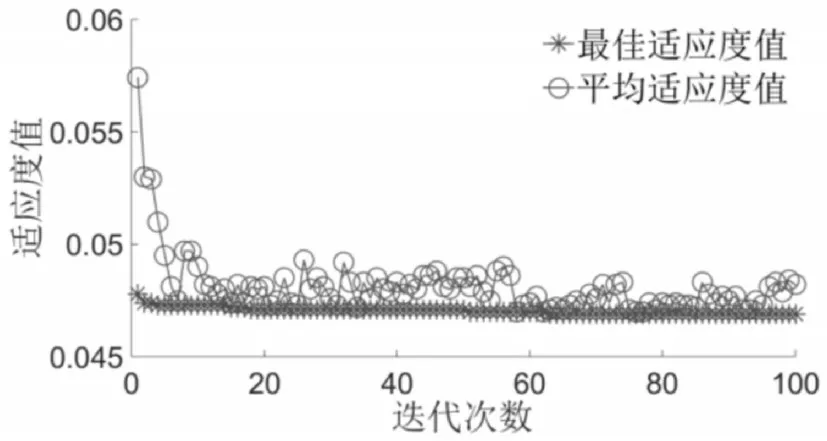
图4 适应度值Fig.4 Fitness Value

表1 SVR预测结果Tab.1 SVR Prediction Results

表2 PSO-SVR预测结果Tab.2 PSO-SVR Prediction Results
从图5和图6可以得出:在50个测试样本中,PSO-SVR的上下排预测穿管阻力值较SVR更接近真实的阻力值,PSO-SVR预测性能更好。SVR的决定系数R2上排穿管为0.875,下排为0.889,而PSO-SVRR2达到了0.94以上,PSO-SVR对模型的解释能力优于SVR;PSO-SVR的预测平均误差(MRE)在4%以内,比SVR的上下排穿管预测准确度分别高4.38%、5.06%,并且PSOSVR的均方根误差(RMSE)更小,表明PSO-SVR的预测能力更强。

图5 上排穿管预测Fig.5 The Upper Row Tube-piercing Prediction

图6 下排穿管预测Fig.6 The Lower Row Tube-piercing Prediction
5 结论
运用PSO-SVR预测穿管机构定位误差得到以下结论:
(1)运用粒子群优化SVR的惩罚因子C和核函数σ,,避免SVR盲目的搜索和“早熟”,优化后的SVR具有更好的泛化能力和较短的时间来实现全局最优搜索。
(2)PSO-SVR可以实现非接触式预测穿管机构定位误差,预测过程耗时短,实现快速预测穿管精度,很好地适应散热器穿管工序的节拍,提高穿管的效率和精度。
