基于AMD和小波阈值去噪的电机轴承故障诊断
2021-09-23朱明斯李飞龙
姜 磊,朱明斯,李飞龙
(1.浙江工业职业技术学院,浙江 绍兴312000;2.北京信息科技大学,北京100101;3.中矿龙科能源科技股份有限公司,北京101300)
1 引言
轴承是异步电机将电能转化为机械能的关键部件,轴承内圈因高速运转而承受较大载荷,是电机所有常见故障类型中发生故障概率最大的部件[1]。文献[2]利用ITT变换方法抑制振动信号中低频杂波和背景噪声对故障特征信号的影响,增强故障信号的冲击特征,从而准确识别出风电机组滚动轴承的故障类型。谢国民等[3]针对电动机中常见的轴承故障,在对机械故障信号进行深入分析的基础上,提出一种基于正交小波的电机故障诊断方法来判断故障部位及类型。文献[3]运用正交小波及专家系统对滚动轴承进行故障诊断取得了一定成效,但是专家系统的建立需要大量故障工作信息,建立过程具有很大难度[4],而且没有相关的数据分析,不能很好的论证所提方法的优越性。目前对异步电动机常用的诊断方法为定子电流谐波检测法,信号处理技术是谐波法异步电机故障诊断技术的核心。小波阈值法具有直观性、操作便利性以及去噪性能较好等特点,所以广泛应用。解析模态分解(AMD)算法[5]可以在确定信号频率成分的前提下进而确定二分频率值对信号进行AMD分解[6],达到从信号中提取频率成分的目的。
本文针对故障谐波信号中含有不同频率谐波的情况,将小波阈值去噪算法与AMD算法相结合,用于实现谐波法电机轴承故障诊断中的特征频率检测,从而提升故障诊断的准确性和可靠性。
2 轴承故障机理分析
轴承故障较为繁琐,出现的故障往往与其结构有关,故障可分为内外圈故障、滚动体和保持体故障,轴承故障时,其特征频率就是振动频率。
滚动轴承故障产生的振动,会引起电机旋转的转轴中心变动。这样使得电机定转子之间的气隙长度发生变化,从而导致电机气隙磁场的磁通波形发生畸变,从而在定子电流中感应出相应频率的谐波电流[7]。下面对轴承内圈、外圈、滚动体故障特征频率的表达式[8-9]进行分析。
轴承在运转时,其保持架的速度Vc为:

式中:Vo—轴承外圈速度;Vi—轴承内圈速度。

式中:Do—轴承外圈直径;no—轴承外圈转速;Di—轴承内圈直径;ni—轴承内圈转速。

式中:Dc—轴承保持架直径;Db—轴承滚动体直径;α—轴承滚动体接触角。
将式(3)和式(2)带入式(1)得:
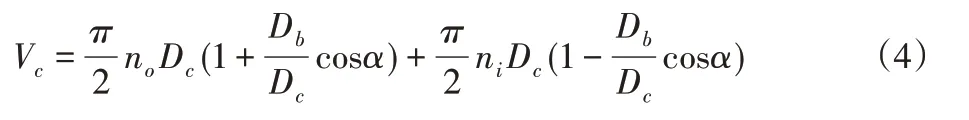
继而可得到保持架的旋转速度nc为:

(1)轴承外圈故障的振动频率fo
根据式(5),可得保持架相对于外圈的旋转速度nco为:

因为保持架与滚动体相对静止,可得一个滚动体相对于外圈的旋转速度nbo为:

对于一个含有N个完全相同的滚动体的轴承来说,滚动体相对于外圈的转速nboN为:

已知,轴承在运转时,其外圈固定在感应电机的保护罩上,内圈与感应电动机转子相连,即

式中:n—感应电动机转子转速。
所以式(8)可改写为:

由式(10)可得到轴承外圈出现故障时的振动频率fo为:

式中:fr—感应电动机转子旋转频率。
(2)轴承内圈故障的振动频率fi
与推导轴承外圈故障的振动频率一样,可以得到电动机轴承内圈出现故障时的振动频率fi:

(3)轴承滚动体故障的振动频率fb
轴承某个滚动体自身的旋转速度nb为:
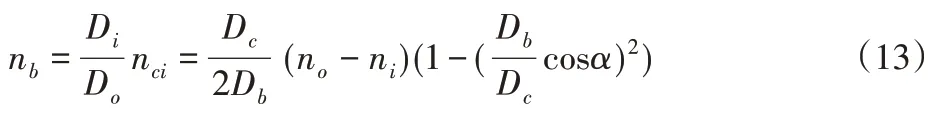
同理可得轴承滚动体出现故障时的振动频率fb为:

(4)轴承保持架故障的振动频率fc
已知保持架的旋转速度nc如公式(5),同理可推出轴承保持架出现故障时的振动频率fc为

感应电动机轴承发生故障时,会使轴承发生特定频率的振动,如fo、fi、fc、fb。轴承类故障在定子电流中所产生的特征频率计算如下:
与轴承外滚道故障对应的定子电流信号特征频率为:

式中,k=1,2,3…;f为电源供电频率。
与轴承内滚道故障相对应的定子电流信号特征频率为:

与轴承滚动体故障相对应的定子电流信号特征频率为:

轴承故障所对应的定子电流谐波信号特征频率不仅与轴承结构有关,也与交流电源频率以及电机转速有关,而且该特征频率幅值较小容易被基波分量旁瓣和噪声淹没。因此,对轴承类故障进行诊断时通常采用振动信号检测方法。
3 小波阈值故障信号去噪分析
小波阈值法去噪的本质是根据预先设定的阈值对变换后的小波系数进行判决,若设定的阈值偏小,去噪后的信号中仍会有大量噪声,其产生的尖峰突起会对特征频率的提取产生干扰,导致故障诊断的误诊;若设定的阈值偏大,则能量较小的有用信号会被当作噪声而阈值化处理掉,这会导致有用信号的能量丢失,使特征频率分量频谱模糊,进一步导致无法诊断出故障类型。
在诊断电机故障信号时,除可用的有效信号外,其还含有大量的噪声,如何有效消除噪声干扰对电机故障诊断的准确性有较大影响。有用信号和噪声的小波分解系数在小波域的不同尺度上分布特性不同,根据这一特点,可以利用小波阈值法进行故障谐波信号去噪。传统的软、硬阈值函数具有重构信号失真和产生震荡、光滑性变差等缺点,本文提出的一种新的阈值函数,可有效客服这些问题。
4 AMD和小波阈值去噪的谐波检测方法
4.1 解析模态分解算法原理
AMD算法原理是将一个时间信号分解为两个信号之和,这两个信号的频谱分布在两个相互排斥的频带内,算法实本质上是一个自适应的低通滤波器,是利用希尔伯特变换将某一特定的频率成分的信号解析分解出来。基于AMD算法能够将时间信号分解成两个时间序列的能力,可用其实现各个频段的滤波功能,且不会产生信号衰减的现象。当预知信号中的频率组成分量时,可从信号中提取预知分量。
4.2 仿真测试分析
针对故障谐波信号中含有不同频率谐波的情况,将小波阈值去噪算法与AMD算法相结合,用于实现谐波法异步电机故障诊断中的特征频率检测。根据上述轴承故障机理分析相关模型使用该方法进行谐波特征频率检测。其中小波分解层数为3层,小波基函数选择“sym6”小波基。原始故障信号及小波阈值去噪后的信号,如图1所示。
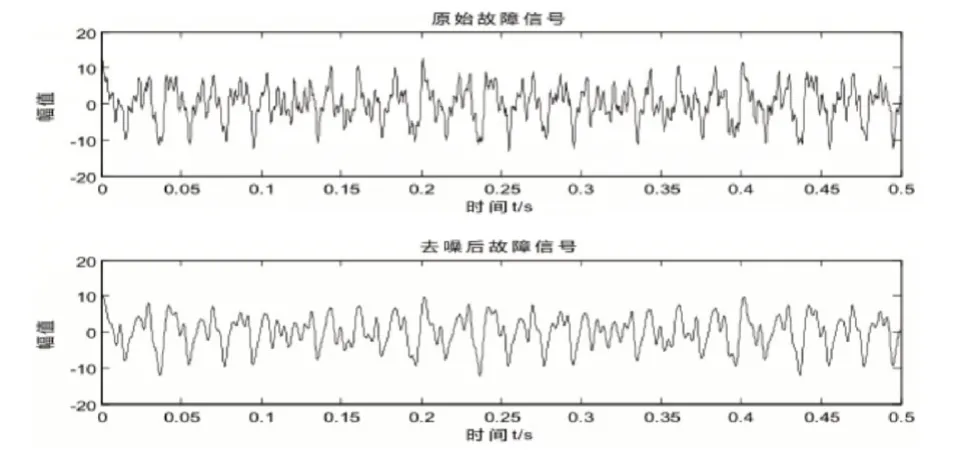
图1 原始信号和去噪后信号Fig.1 Original Signal and Denoised Signal
用AMD算法对去噪后的信号进行分解,分解出的各个分量的时域波形图,如图2所示。

图2 去噪后信号AMD分解结果Fig.2 Theresult Ofsignal AMD Decomposition After Denoising
用AMD对去噪后的信号进行分解,分解出的各个频率分量很好的保留了谐波原有的特性,去噪效果良好。图2中所示的个分量频谱图,如图3所示。
如图3所示,在各个IMF分量的频谱中可以看出原始信号中所包含的6次、3.5次、2次、1.4次和0.9次谐波间谐波和基波均被准确的分解提取出。综合上述分析,将基于分层阈值和新阈值函数的小波阈值去噪算法与AMD算法相结合用于电动机轴承故障信号谐波检测具有可行性。

图3 AMD分解结果中各IMF分量频谱图Fig.3 Spectrum of IMF Components in AMD Decomposition Results
4.3 轴承故障特征提取实例
根据前面轴承故障机理分析所述,电机轴承故障的特征频率可以通过计算公式计算出,即所要提取的频率成分是预知的,这符合AMD分解算法的基本要求。实验数据选用的故障电机的参数为:单点损伤的直径和深度分别为0.5334mm、0.2794mm。轴承转速为1750r/min,轴承直径为39.04mm,滚动体直径为:7.94mm,滚动体个数为:9个,触角为00,采样频率为12000Hz,采样点数为6000。依据轴承故障机理分析研究的轴承故障特征频率计算公式可以得出不同故障的特征频率,外圈故障对应107Hz,内圈故障对应162Hz,滚动体故障对应141Hz,保持架故障对应12Hz。下面对电动机轴承振动信号进行分析和处理,振动信号时域波形图,如图4所示。

图4 轴承故障信号时域图Fig.4 Time Domain Diagram of Bearing Fault Signal
用小波阈值去噪发对故障信号进行去噪,去噪后的时域波形图,如图5所示。

图5 去噪后故障信号时域图Fig.5 Time Domain Diagram of Fault Signal After Denoising
用AMD算法对去噪后的故障信号进行分解,分解成了7个内禀模态函数(IMF)分量和一个余量,由于最后一个分量频率过低,这里将最后一个IMF和余量均忽略,只显示前6个IMF分量,其时域波形图。
分解出的IMF1分量和IMF2分量具有频率高、持续时间段、幅值小能量低的特点,因此可以判断出这两个分量是残留的噪声。图7为6个IMF分量的频谱图,如图6所示。

图6 轴承故障信号AMD分解结果Fig.6 Decomposition Result of Bearing Fault Signal AMD
IMF6分量包含了故障特征频率142Hz和162Hz,这两个频率分量与前面分析的轴承滚动体故障特征频率和内圈故障频率相符,说明该电动机出现了这两种故障,通过本方法准确的检测出了电动机故障谐波分量,并进一步诊断出了故障类型,在IMF6中出现的其他频率成分是由噪声和负载振动等因素的影响,如图7所示。
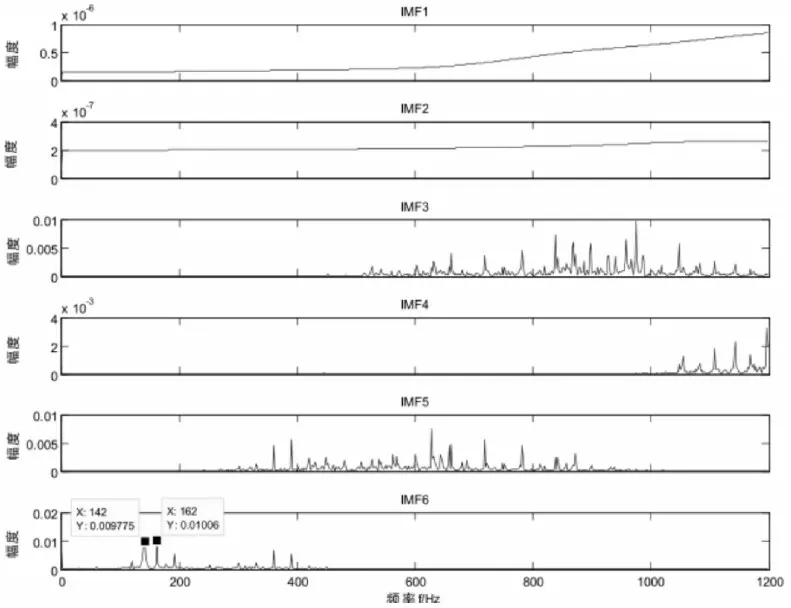
图7 AMD分解结果IMF分量频谱图Fig.7 IMF Component Spectrum of AMD Decomposition Results
5 结论
本文运用AMD算法对信号特征频率分量提取,通过模拟仿真验证了算法的准确性。由于电动机故障谐波信号频率成分可以通过故障机理公式计算得出,这与AMD算法在提取特征频率时需预知频率成分的前提相符。因此,提出将小波阈值去噪算法和AMD算法相结合的电动机故障信号谐波检测的方法,通过对同时具有轴承内圈故障和滚动体故障的电动机振动故障谐波信号分析和处理,准确的提取出故障特征频率,验证了该方法的准确性和有效性。
