基于遗传模拟退火算法改进BP神经网络的中长期电力负荷预测

徐 扬 张紫涛

基于遗传模拟退火算法改进BP神经网络的中长期电力负荷预测

徐 扬 张紫涛

（河海大学能源与电气学院，南京 211100）

针对目前中长期负荷预测方法中存在过拟合、预测精度和效率较低等问题，本文提出一种基于遗传模拟退火算法（GSA）改进BP神经网络的中长期电力负荷预测模型，即BP-GSA模型。首先建立标准三层神经网络，即输入层、隐藏层和输出层，选择国民生产总值、第二产业生产总值、市区常驻人口及月平均温度四个影响因子作为输入变量，月度负荷为输出变量。其次利用遗传模拟退火算法不断修正网络节点连接权值，以最优适应度为标准，确定最优网络节点连接权值分布。最后，代入权值最优解，通过训练样本数据，获取最小方均差预测模型。分别应用本文提出的BP-GSA模型及其他四种传统方法，对某市2020年月度负荷进行预测。误差分析表明，BP-GSA模型预测精度最高。随后将BP-GSA模型分别应用于不同年份的月度负荷预测，预测结果表明其误差稳定，证明了模型的鲁棒性。

负荷预测；遗传算法；模拟退火；BP神经网络

0 引言

随着负荷种类的多样化和我国电力市场的逐渐完善，负荷预测成为电力调度的重要一环。负荷预测主要分为长期、中期和短期预测三大类。对于全社会而言，由于GDP增长情况与全社会用电量变化趋势基本保持一致，因此中长期负荷预测尤为重要。但是中长期负荷预测所需数据集较大、时间跨度较长，不确定影响因素多[1]。传统的中长期电力负荷预测模型（例如时间序列模型[2]，多回归分析模 型[3-5]，累积平均气温模型[6]）过于简单，无法准确模拟中长期电力负荷的阶段性特征。

近年来，由于深度学习算法在处理非线性因素时具有良好的性能，因此被广泛应用于中长期负荷预测。文献[7]通过构建多变量灰色遗传的中长期负荷预测模型，显著提高预测精度；文献[8]基于大数据聚类方法进行了中长期负荷预测，有效避免复杂的调参过程，提高了预测效率；采用Dempster合成法则和Yager组合规则，文献[9]提出一种基于改进的证据理论的中长期负荷预测方法。

上述文献所提出的负荷预测方法均为单一结构模型，预测能力有限，准确性仍有待提高，因此组合预测模型得到广泛应用。文献[10]将灰色Verhulst模型与等维新息灰色理论线性组合，充分发挥了灰色Verhulst模型所需数据少、不受特定负荷数据及等维新息灰色理论影响的优势；但是该模型针对不同数据样本的结果波动较大，鲁棒性有待提高。文献[11]提出了一种基于数据分组处理方法来优化粒子群算法-最小二乘支持向量机（particle swarm optimization-least squares support vector machine, PSO-LSSVM）的中长期电力负荷预测模型，由于核函数的选取直接影响支持向量机性能优劣，而目前有关核函数及其参数选取的相关文献较少，因此该方法具有一定的随机性。文献[12]基于马尔科夫-云模型，提出了一种预测模型筛选与变权重组合预测的方法，兼顾了负荷预测的效率和精度，但是在处理噪声数据时，该模型性能较差。文献[13]提出一种组合残差与修正的BP神经网络（back propagation neural network, BPNN）模型，拟合精度和可靠性均得到提高，但是文章中没有直接的方法指导神经网络的开发，其结构主要由重复的试验决定，需要更多的训练时间。此外，上述模型均没有考虑预测过程中的过拟合问题，实际预测性能有待提高。

因此，针对上述问题，本文提出一种基于遗传模拟退火算法改进BP神经网络（BP neural network improved by genetic simulated annealing algorithm, BP-GSA）的中长期电力负荷预测模型。该模型选择大规模历史数据作为神经网络的训练集，并通过遗传模拟退火算法修正神经网络节点的连接权值。由于该修正具有试探性，因此网络在训练过程中可以避免陷入极小值点，解决了现阶段中长期负荷预测模型存在的过拟合问题。实际算例表明，BP-GSA模型避免了复杂的参数设置，在预测精度和预测效率方面，均优于其他方法，且具有良好的鲁棒性。

1 理论基础

1.1 标准BP神经网络

标准BP神经网络由误差反向传播算法训练而成，是一种三层前馈网络，即输入层、隐藏层和输出层，标准BP神经网络拓扑如图1所示。BP神经网络通过监督学习方法进行训练，该学习方法包括信号的正向传播和误差的反向传播。在正向传播过程中，如果输出层的信息不符合预期，则通过隐藏层将输入信息传输到输出层，然后进入反向传播过程，即期望输出和实际输出之间的误差从输出层进入隐藏层，并经过连接节点权重和阈值的不断修改而减少。重复此过程，以使整个网络朝误差减少的方向更正，直到将误差减少到目标值为止。

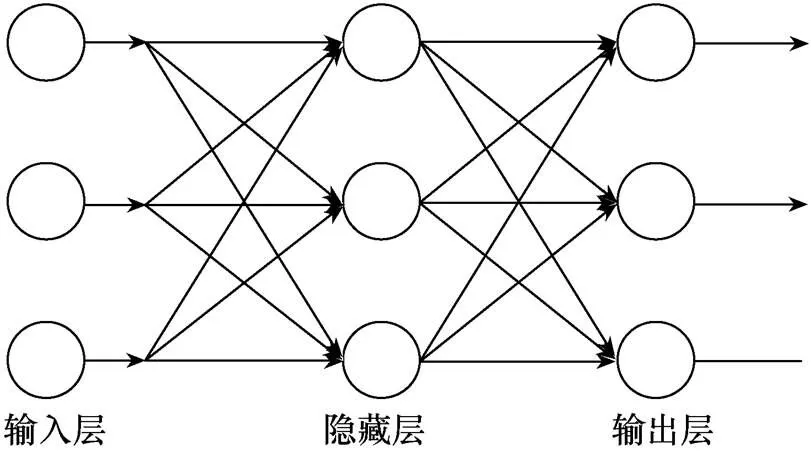
图1 标准BP神经网络拓扑

1.2 遗传模拟退火算法

遗传算法（genetic algorithm, GA）是一种由自然进化过程衍生出来的算法，并成为一种基于生物学的杰出随机搜索技术。GA首先从一组初始的随机解决方案开始，将每一个目标编码为一条染色体，代表问题的解。在连续迭代过程中，染色体不断进化，并基于适应度的标准来评判该染色体是否为最优解。其后代是通过使用交叉算子将当前一代的两个染色体合并或使用突变算子对染色体修饰而形成。

模拟退火（simulated annealing, SA）算法灵感来自于温度变化的过程，该过程导致固体加热和冷却后能量发生变化。SA具有很强的局部搜索能力。根据Metropolis标准的概率规则，可以接受目标函数的增加。该标准依赖控制参数，类似于物理退火，因此被称为系统温度。SA在温度不断下降过程中通过重复采样，得到问题的全局最优解。

遗传模拟退火（genetic simulated annealing, GSA）算法以提高效率为目的，将上述两种算法相组合。GSA算法既保留了遗传算法全局搜索的优点，又结合了模拟退火算法局部搜索的长处。GSA算法本质上是从一组随机产生的初始解开始，进行最优解搜索[14]。首先基于一系列遗传操作产生一组新的个体，然后引入SA过程进行修正，该过程类似于随机梯度下降法，最后将退火结果作为新个体。

2 遗传模拟退火算法优化的BP神经网络

2.1 BP-GSA原理

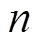
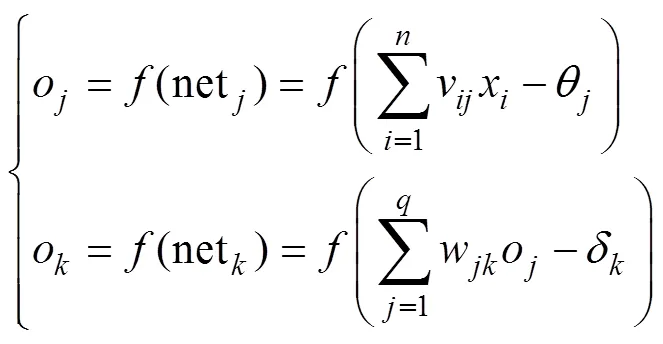
式中：x为输入层样本数据；net, net分别为隐藏层第个节点和输出层第个节点的净输入；θ、δ分别为隐藏层第个节点和输出层第个节点的阈值；(net)为sigmod函数，即

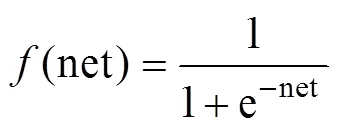
误差反向阶段，误差信号为

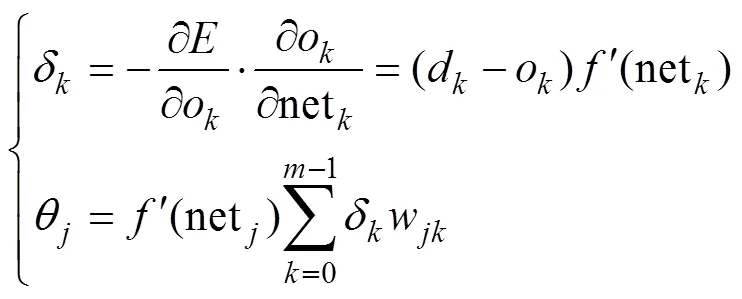
式中：为总误差；d为样本的期望输出；o为神经元的实际输出。

权值修正量为

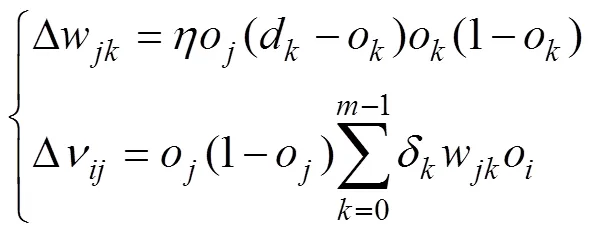
根据式（4）可知，由于权值的确定性，神经网络算法极值容易过早出现，具有较低的局部搜索能力，但该算法的全局搜索能力很强。相反，遗传模拟退火算法具有一定局部搜索能力，但必须经过反复的退火操作才能进入最优过程，因而运行效率不高。因此，若通过GSA对神经网络节点的权值进行修正，将大大提高运行效率和准确度。对式（4）做出如下调整，有

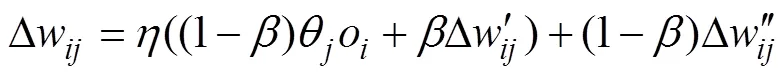
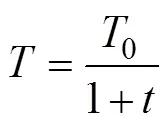
此时，适应度F的计算式为

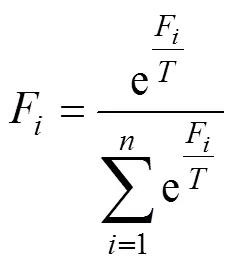
2.2 BP-GSA算法流程

基于遗传模拟退火算法的BP神经网络模型主要分为网络结构确定、遗传模拟退火算法优化和神经网络预测三部分。BP-GSA算法流程框图如图2所示，具体步骤如下[15-16]：

1）初始化。确定BP神经网络输入层、隐藏层和输出层的节点数及退火初始温度、退火次数、种群规模、交叉概率、变异概率相关参数初始值。

2）二进制编码。对网络权值进行二进制编码。使用一组二进制数表示一组网络权值分布，即个体。

3）产生新个体。采用选择、交叉、变异一系列操作，产生新的网络权值分布，即新个体。

4）模拟退火。按照Metropolis概率标准剔除一部分新个体。

5）适应度判断。按照式（8）计算新个体适应度。判断是否满足适应度要求，不满足转3）。

6）训练。代入最佳节点权值，训练样本数据。

7）计算训练结果方均差（mean squared error, MSE），判断是否满足误差允许范围，不满足转6）。

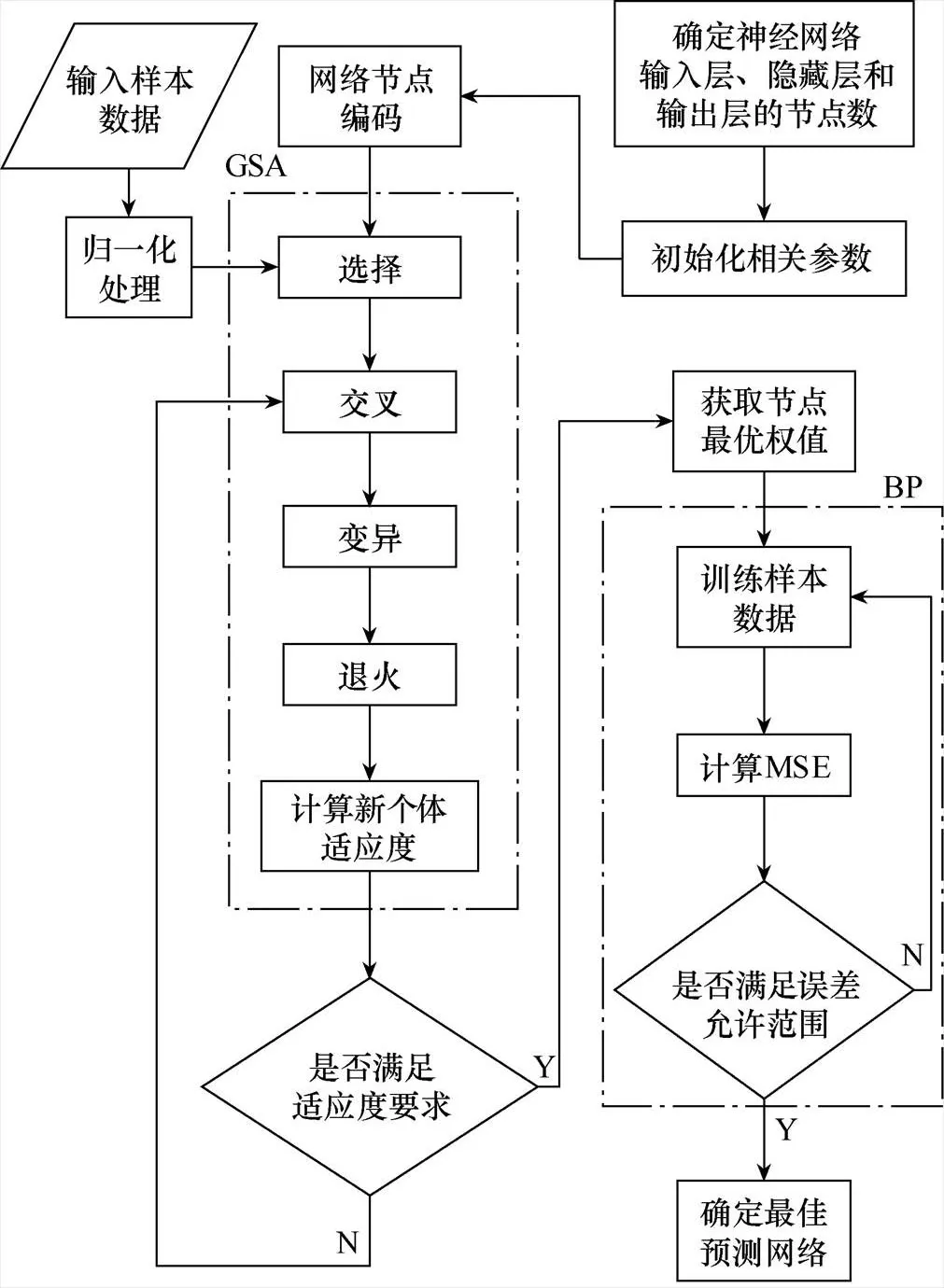
图2 BP-GSA算法流程框图

3 算例及分析

为验证BP-GSA模型预测效果，本文以某市2001年1月至2019年12月的月度负荷数据为网络输出变量，以国民生产总值（GDP）、第二产业生产总值（GDP2）、市区常驻人口（POP）及月平均温度（TEM）四个影响因子作为输入变量，建立了算例仿真模型。既考虑到样本代表性、均衡性和用电负荷的自身特点，避免维数过多、信息量过剩，又注意到中长期电力负荷变化趋势与社会生产发展、气候环境紧密相关。另外，经过计算可知，该地区每月工业负荷比重均在70%以上，部分月份达到80%。因此该市负荷变化趋势主要受工业负荷影响，总体相对平稳。

3.1 数据预处理

上述GDP和GDP2均为季度数据，因此，为了与月度负荷数据匹配，通过式（9）计算月平均数值代入模型。

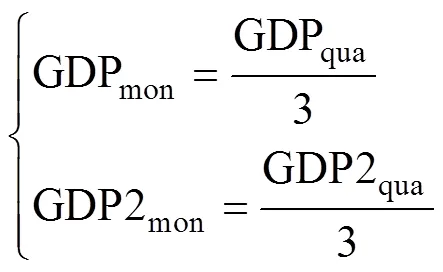
式中：GDPqua和GDP2qua分别为每季度国民生产总值和第二产业生产总值；GDPmon和GDP2mon分别为该季度每月平均国民生产总值和第二产业生产总值。

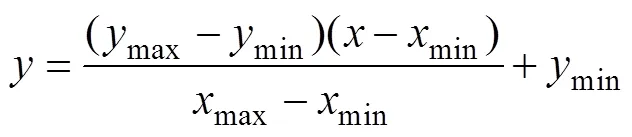
3.2 模型求解

1）BP-GSA模型预测

表1 BP-GSA模型参数

本文设计的神经网络结构如图3所示。

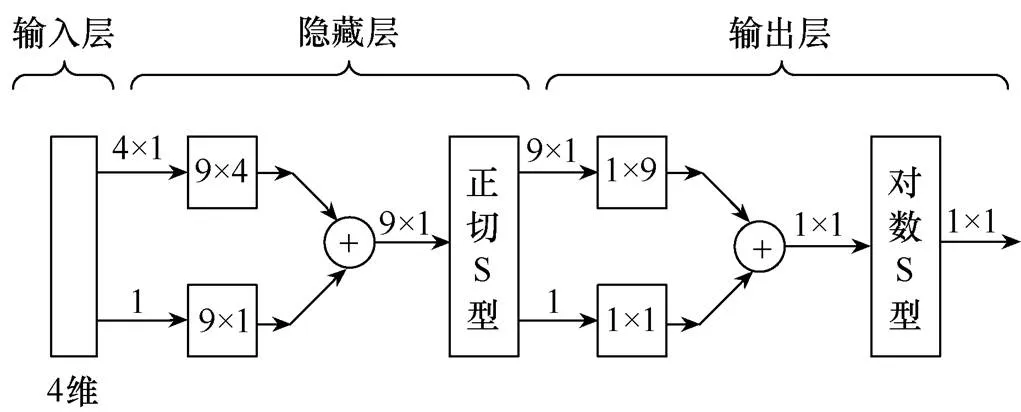
图3 本文设计的神经网络结构

根据图3及表1，利用Matlab编写BP-GSA算法。在确定网络节点最佳权值后，本文分别采用莱文贝格-马夸特方法（Levenberg-Marquardt, LM）、贝叶斯正则化方法和量化共轭梯度法进行训练，最终LM训练所得结果的MSE最小，运算速度较快，LM训练结果如图4所示。

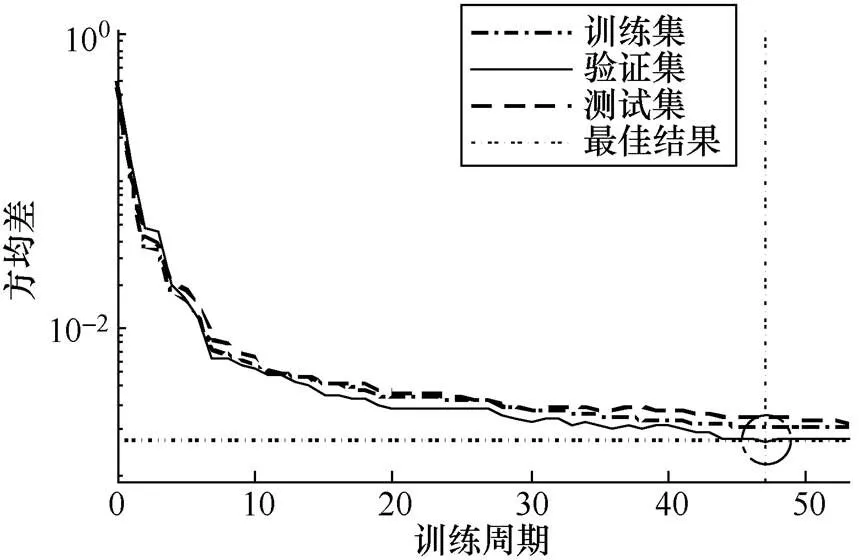
图4 LM训练结果

根据图4可得，模型在第53个训练周期后停止，而最佳的验证性能则出现在第47个训练周期，此时神经网络模型MSE达到最小值，所以该网络为最佳模型。为检验拟合效果，本文将训练集、验证集和测试集的输出结果与目标值进行回归，回归结果如图5所示。

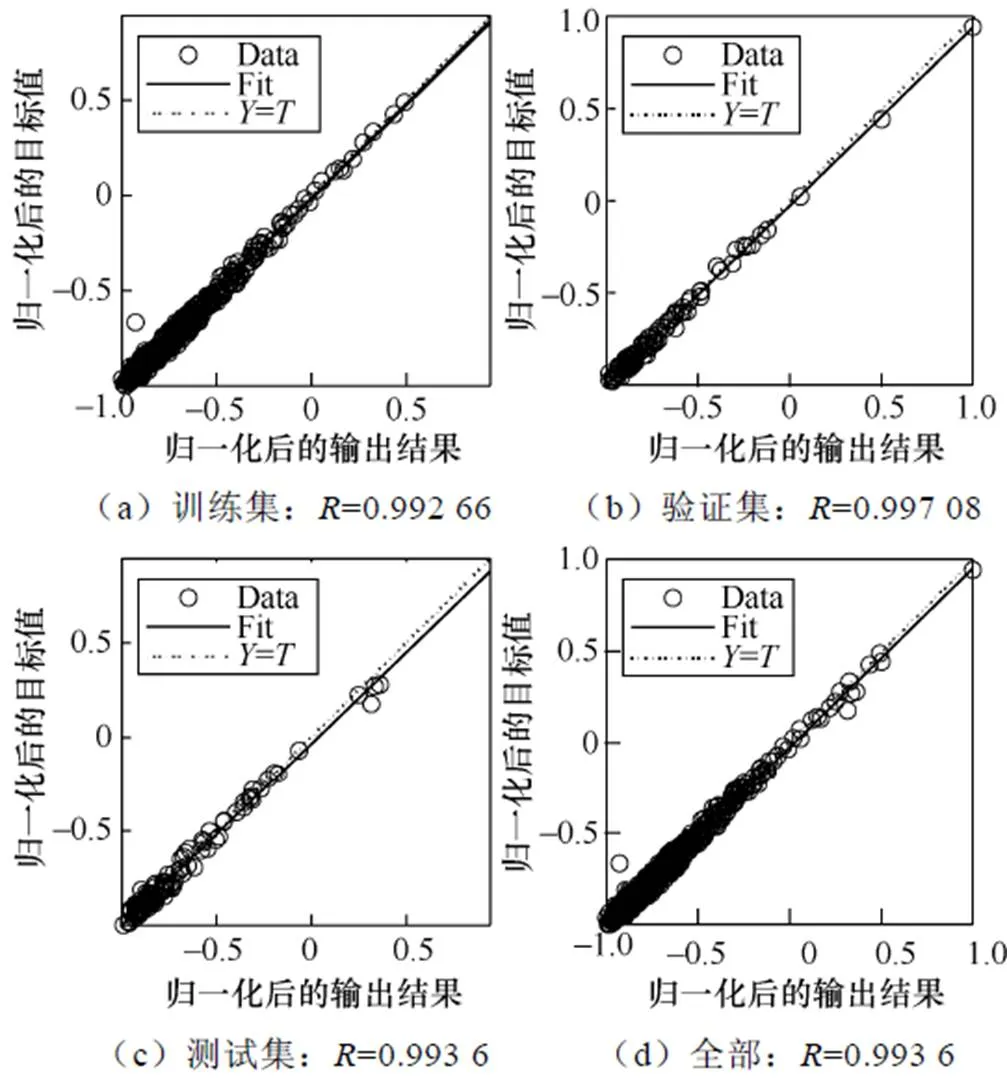
图5 回归结果

图5中，目标值和输出值之间的关系通过相关系数进行评价。如果越接近于1，则模型的预测能力越好。根据图5，相关系数均大于0.99，表明该训练所得模型具有良好的预测能力。将最佳训练模型作为最终的预测模型，对2020年每月用电量进行预测，结果如图6所示。

2）传统模型预测

为验证BP-GSA预测模型较其他模型的优越性，本文利用极限学习机（extreme learning machine, ELM）、支持向量机（support vector machine, SVM）、BP神经网络和小波神经网络（wavelet neural network, WNN）四种传统方法对该市负荷进行预测，传统模型预测结果如图7所示。

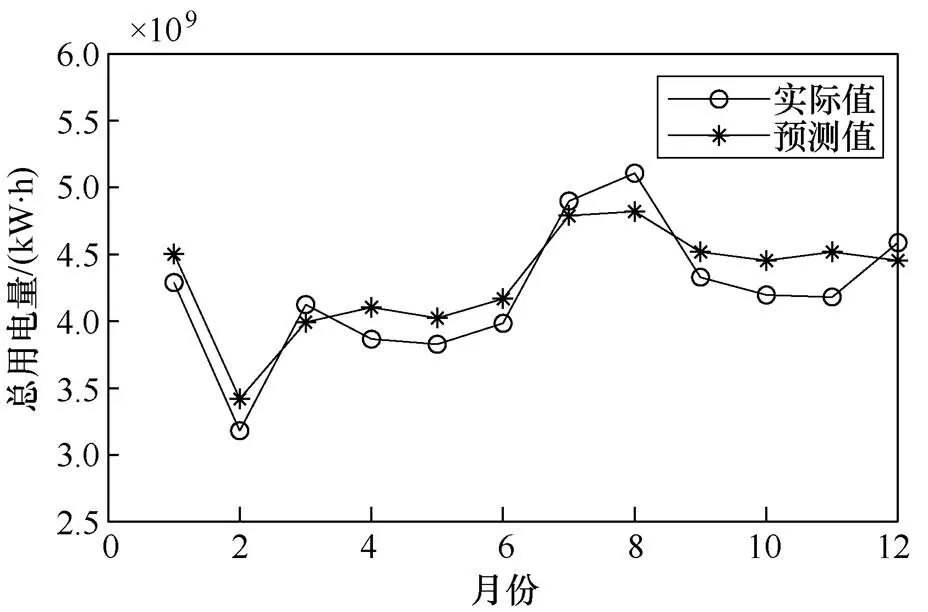
图6 BP-GSA模型预测结果

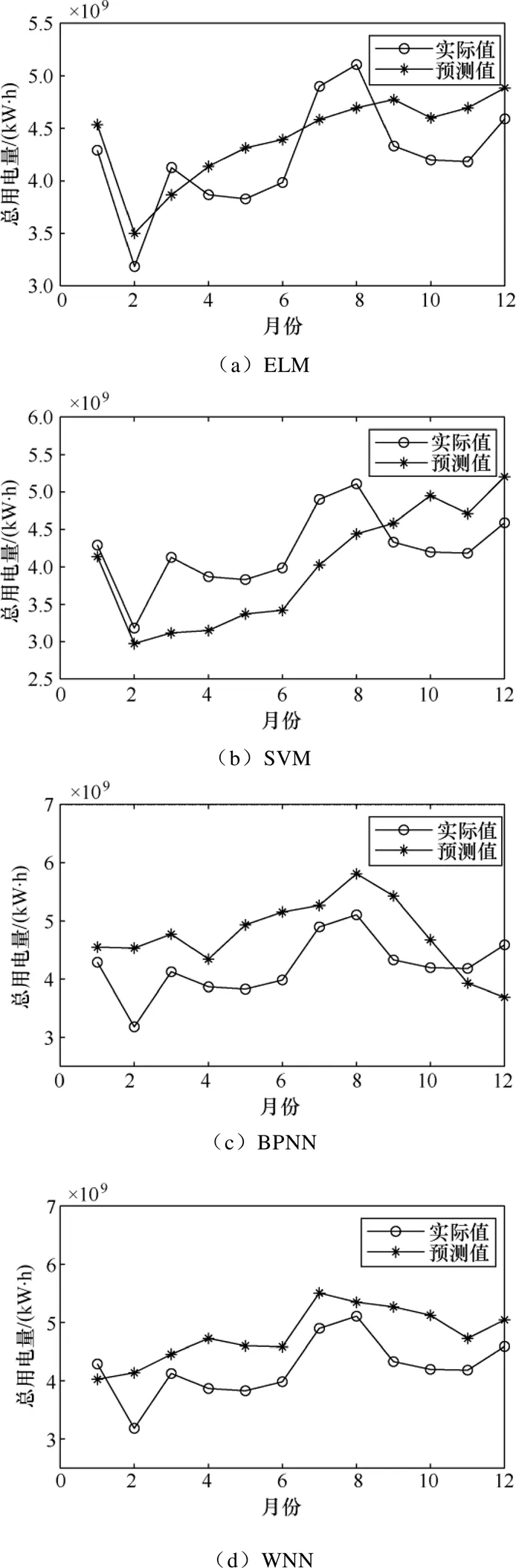
图7 传统模型预测结果

3.3 结果分析

作出BP-GSA模型和上述四个传统模型的误差曲线，如图8所示。

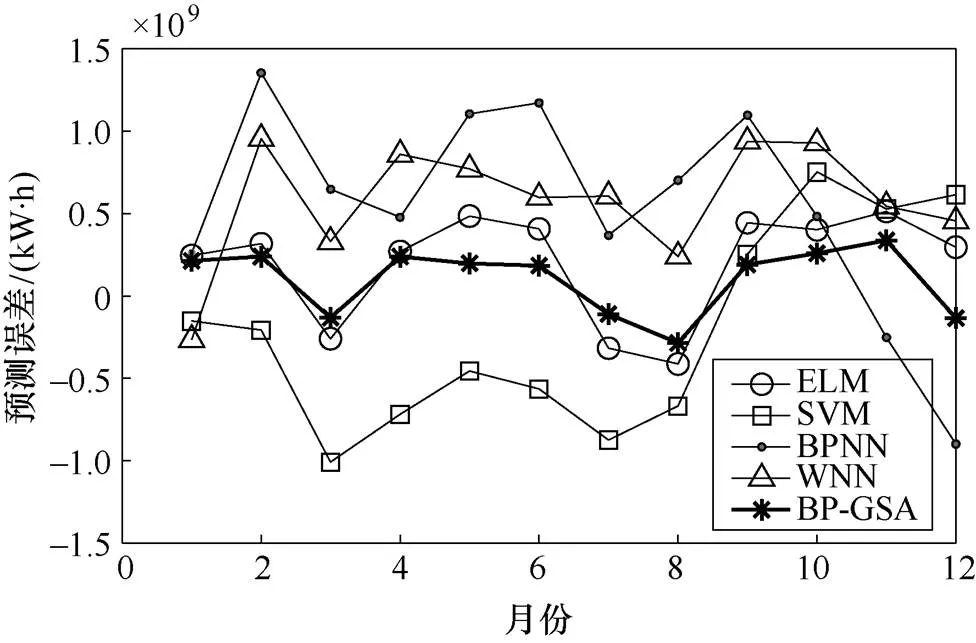
图8 误差曲线

由图6～图8可知，BP-GSA模型得到的预测值最接近原始值，预测曲线几乎与原始负荷曲线重合，且误差曲线在零值附近小幅波动，误差最小。此外，观察图6可得，2020年除3月、7月及8月个别月份外，月度负荷实际值均低于BP-GSA模型所得预测值，考虑到该市高比例工业负荷的实际情况及2020年工业发展受疫情冲击的突发状况，说明负荷实际变化趋势还受现实突发因素的影响。

进一步分析，该市2020年月度负荷预测结果见表2。根据表2及式（11）～式（14）分别求取最大误差（maximum error, ME）、平均相对误差（mean relative error, MRE）、平均绝对误差（mean absolute error, MAE）、方均根误差（root mean square error, RMSE）。

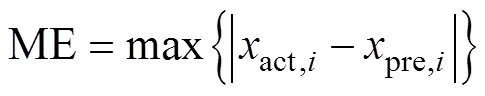
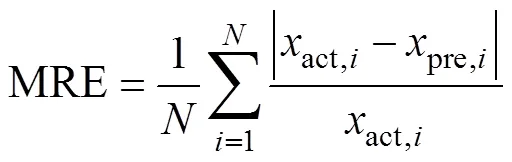
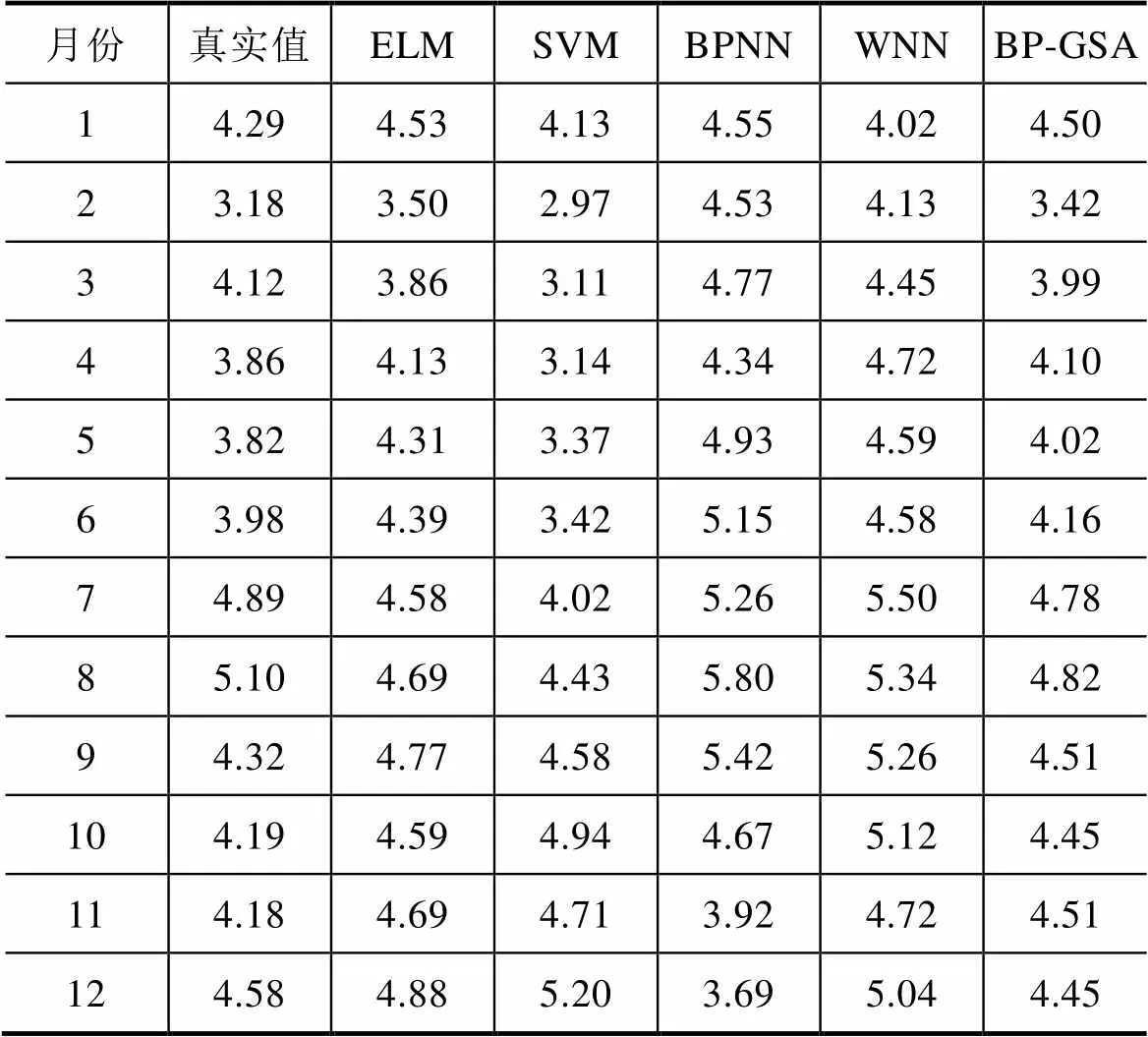
表2 2020年12个月预测值 单位：×109kW·h

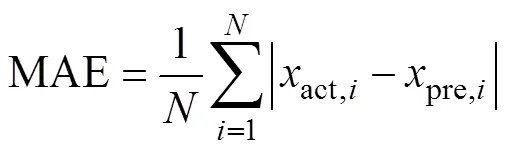
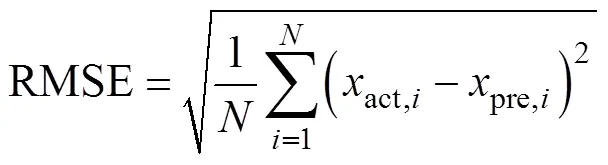
式中：act,、pre,i分别为2020年第个月实际值和预测值；为预测样本数，本文表示12个月，即12。

误差计算结果见表3。

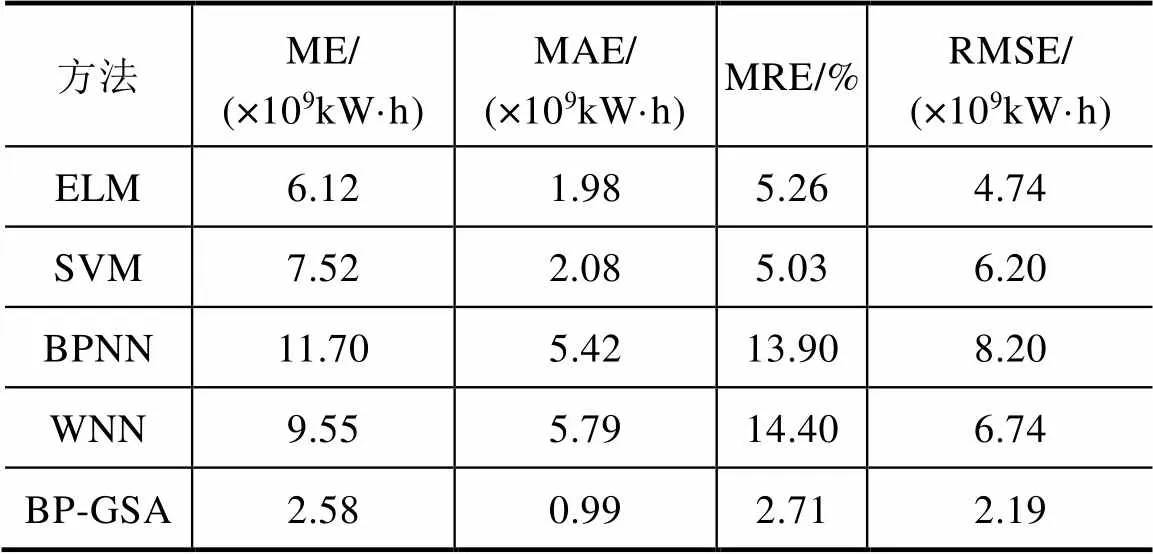
表3 误差计算结果一

分析表3数据可知，与其他模型相比，BP-GSA模型预测效果最佳，预测精度大幅度提高。经过GSA算法改进后的BP神经网络，能够充分提取出负荷的变化特征，既包含不同年份、相同月份负荷的变化特征，又包含同一年份、不同月份负荷的变化特征。且由于GSA算法的优化，BP神经网络在进行训练时，可以有效避免样本数据中由于突发情况所造成的不正常数据的影响，大大提高预测结果的准确性。

为检验BP-GSA模型的鲁棒性，本文分别以2016年、2017年、2018年、2019年的月度负荷数据为测试集，2001年至预测年份前一年的负荷数据为训练集，通过该模型进行了预测，其误差计算结果见表4。

表4 误差计算结果二

由表3及表4可知，当预测年份发生变化时，采用BP-GSA模型预测的月度负荷误差基本相同，说明BP-GSA模型具有良好的鲁棒性。

4 结论

针对电力负荷预测中传统预测模型的的局限性，本文提出了BP-GSA模型，具有如下优点：

1）通过GSA算法修正网络节点连接权值，避免网络陷入极小值点，解决了现阶段负荷预测模型所存在的过拟合问题。

2）实际算例表明，在预测精度及处理大规模样本数据集的效率方面，BP-GSA模型均优于其他方法，且避免了复杂参数设置，具有广阔的发展和应用前景。

3）通过对不同年份的月度负荷分别做出预测，模型预测结果与实际值的误差保持稳定，说明本文提出的BP-GSA模型具有良好的鲁棒性。

此外，实际中长期负荷变化趋势还受疫情等突发状况的影响，在今后的研究中，可在BP-GSA模型中引入突发状况影响因子，进一步提高中长期负荷预测的精度。

[1] 魏华栋, 陶媛, 蔡昌春, 等. 基于改进长短期记忆神经网络的短期负荷预测[J]. 电测与仪表, 2020, 57(19): 93-98.

[2] 张帅, 杨晶显, 刘继春, 等. 基于多尺度时序建模与估计的电力负荷数据恢复[J]. 电工技术学报, 2020, 35(13): 2736-2746.

[3] 张敏, 钱霜秋, 吴仲麒, 等. 基于数据挖掘技术的中长期负荷预测方法[J]. 电气技术, 2021, 22(6): 43-48.

[4] 陈毅波, 郑玲, 姚建刚. 基于粗糙集理论与D-S证据理论改进的多元回归负荷预测方法研究[J]. 电力系统保护与控制, 2016, 44(6): 62-67.

[5] 李滨, 覃芳璐, 吴茵, 等. 基于模糊信息粒化与多策略灵敏度的短期日负荷曲线预测[J]. 电工技术学报, 2017, 32(9): 149-159.

[6] 潘文虎, 夏友斌, 宋铭敏, 等. 基于累积平均气温模型的气象负荷预测[J]. 电气技术, 2020, 21(4): 67-70.

[7] 陈先飞, 何山, 王杰, 等. 基于MGM(1, n, r)的主动配电网中长期负荷预测[J]. 太阳能学报, 2020, 41(2): 189-193.

[8] 徐源, 程潜善, 李阳, 等. 基于大数据聚类的电力系统中长期负荷预测[J]. 电力系统及其自动化学报, 2017, 29(8): 44-48.

[9] 吴耀武, 娄素华, 卢斯煜, 等. 基于改进的D-S证据理论的中长期负荷预测方法[J]. 电工技术学报, 2012, 27(8): 158-162.

[10] 林天祥, 张宇. 灰色Verhulst与等维新息组合模型在中长期负荷预测中的研究[J]. 电气技术, 2017, 18(3): 42-46.

[11] 龙金莲, 卢家暄, 张玉. 基于GMDH-PSO-LSSVM中长期电力负荷预测[J]. 贵州大学学报(自然科学版), 2017, 34(6): 50-53.

[12] 尹星露, 肖先勇, 孙晓璐. 基于预测有效度和马尔科夫-云模型的母线负荷预测模型筛选与变权重组合预测[J]. 电力自动化设备, 2015, 35(3): 114-119.

[13] 宋建, 束洪春, 董俊, 等. 基于GM(1, 1)与BP神经网络的综合负荷预测[J]. 电力建设, 2020, 41(5): 75-80.

[14] 蒋美云. 基于模拟退火算法优化的BP神经网络预测模型[J]. 软件工程, 2018(7): 36-38.

[15] 郭彩杏, 郭晓金, 柏林江. 改进遗传模拟退火算法优化BP算法研究[J]. 小型微型计算机系统, 2019, 40(10): 2063-2067.

[16] 张巨林. 基于模拟退火优化BP神经网络的变形监测数据预测方法[J]. 测控技术, 2020, 39(11): 57-62.

Medium and long-term power load forecasting based on BP neural network improved by genetic simulated annealing algorithm

XU Yang ZHANG Zitao

(College of Energy and Electric Engineering, Hohai University, Nanjing 211100)

Aiming at the problems of over-fitting, low accuracy and low efficiency in current medium and long-term load forecasting methods, a novel model, which is based on improved BP neural network (BP-GSA), is proposed. Firstly, a standard three-layer neural network including the input layer, the hidden layer and the output layer is established. The paper selects GDP, secondary industry GDP, urban resident population, monthly average temperature as input variables, and monthly load as the output variable. Secondly, the genetic simulated annealing algorithm is used to continuously modify the network node connection weights until the optimal network node connection weight distribution is achieved according to the optimal fitness standard. Finally, with the optimal solution of weights substituted, the paper obtains the model that has the minimum mean square error through the training of the data. The calculation example compares the BP-GSA model proposed in the paper with the other four types of traditional methods by predicting one city’s monthly load in 2020. The error analysis shows that the BP-GSA provides the best prediction. Then the model is applied to other different years. The error remains stable, which verifies the robustness of the algorithm.

load forecasting; genetic algorithm (GA); simulated annealing; BP neural network

2021-03-11

2021-03-28

徐 扬（1999—），男，江苏省常州市人，本科，主要研究方向为电力系统及其自动化。