基于模拟退火法寻优的公路边坡抗剪强度参数反分析研究

张晓军, 曹 娟

(1.湖南省交通科学研究院有限公司， 湖南 长沙 410015; 2.湖南金沙路桥建设有限公司， 湖南 长沙 410100)

0 引言

随着我国公路建设事业的快速发展，公路技术人员积累了大量的工程建设资料和经验，在此前提下，为削减勘探和土工试验成本，对许多边坡工程采用经验法或者类比法来估算边坡的抗剪强度参数[1]。此类方法尽管操作简单方便，但受人员工程建设经验、岩土体所处地域差异等不确定因素影响，存在一定局限性。反分析法是获取边坡岩土体参数的一种间接方法，即以现场监测信息为基础，通过反分析模型或算法反推得到岩土体的实际材料参数[2]。

国外岩土工程反分析研究始于上世纪70年代，目前已得到了长足的应用与发展。Finno等[3]利用与误差函数拓扑相关的梯度方法和遗传算法，根据岩体原位测试数据反推Mohr-Coulomb模型的参数。Deb等[4]统计了大量岩体位移数据，利用BP神经网络和模糊系统间接估计岩体的变形模量。Yazdani等[5]利用数值仿真计算替代现场监测，通过位移计算值对Siah Bisheh电站附近岩体参数、应变率以及节理参数进行反演，发现将数值计算结果作为反分析的依据具有可行性。国内方面，传统的边坡参数反分析往往基于剩余推力法[6]、极限分析法[7]和传递系数法[8]进行，而计算科学的进步促进反分析的手段逐渐向智能算法方向发展。张志增等[9]设计了正交试验表，利用有限差分和人工神经网络进行边坡岩体力学参数的反分析。李南生等[10]为克服常规最优化方法在解决非线性问题中的缺陷，利用MATLAB进行了基于遗传算法的边坡反分析研究。张晓咏等[11]将ABAQUS有限元分析与强度折减法进行结合，对稳定渗流作用下的边坡进行了抗剪切强度参数反分析。

实际边坡工程中的反分析问题大多是非线性问题，若采用传统优化方法存在速率低、无解性、多解性、稳定性差等缺陷。本文利用模拟退火法(SA)的优势，将其引入到边坡岩体抗剪强度参数反分析中，形成结合模拟退火法与多点位移优化进行反分析的方法，并以湖南省某高速公路2处边坡为例，编写了模拟退火法反分析程序，探讨和验证了该方法的可行性，研究结果可为边坡分析和设计提供一定的参考。

1 模拟退火原理

在冶金学中，将材料加热后，原子的能量会增大，导致原子容易离开原来的位置随机移动而处于不稳定状态；但温度降低，原子的能量会减弱，移动能力会被削减，如果冷却速率选择恰当，原子就很有可能停留在能量更低的位置，这个过程就是退火[12]。如果将该原理引入寻优过程中，就形成了模拟退火法(SA)。在模拟退火法中，最优化问题的目标函数可被视为原子能量，为了获取目标函数的全局极小值，可以先假定一个初始搜索模型，这就相当于退火中原子能量的初始值，采用合适的降温速度，那么目标函数就有可能向降低的方向移动，使搜索参数逐渐收敛。

根据统计热力学定律，分子在温度T时，处于某种状态Ei满足Boltzmann率分布：

(1)

式中：T为绝对温度；kb为玻尔兹曼常数；Z(T)为分配函数，即各个状态相对几率的总和。

物体从状态i跃迁到状态j的概率为：

(2)

如果，将模型参数向量m视为物体的某种状态，将目标函数E(m)等效为物体的能量函数，利用控制参数T模拟物体的温度，就可以得到Metropolis接受准则[13]：

Pmi→mj=

(3)

从式(3)可以看出，当新模型的目标函数较小时，新模型100%将被接受，从而保证搜索向最优模型的方向移动；而新模型的目标函数较大时，也不会完全被拒绝，而是按照一定的概率接受该模型，这样可以防止过快收敛而陷入局部极值，能够有一定的概率跳出局部极值的陷阱，体现了全局化寻优的特点。

2 基于SA的边坡岩体抗剪强度参数反演

在所研究边坡岩体抗剪强度参数未知的情况下，利用模拟退火法(SA)进行参数反演的过程如下：

1)首先建立有限元模型，在计算能力满足的情况下尽可能多设置几组位移数据提取节点。对有限元模型输入初始的抗剪强度参数c0和φ0，设定多组强度折减系数，进行有限元分析，然后提取各个节点在不同强度折减系数下的位移。

2)建立各个节点的位移-折减系数关系曲线，并进行函数拟合。

3)实际边坡开挖后，在上述各个节点进行位移监测，获取边坡开挖后上述各个节点的监测位移稳定值。

4)根据计算数据和监测数据设定目标函数，编写模拟退火法寻优程序，搜索获取最优强度折减系数。

5)将初始抗剪强度参数按最优强度折减系数进行折减，得到反分析结果，进行误差分析。

3 工程案例

3.1 工程概况

以湖南省某公路的2处边坡为案例，对抗剪强度参数反演方法进行验证。进行反分析的2处边坡概况如下,现场如图1所示。

a) A边坡

b) B边坡

1) K43+700～K43+800右边坡(简称A边坡)，3级坡，基岩为中风化砂质板岩，褐黄-青灰色，变余砂质结构，板状构造，岩体较为完整，边坡1级坡坡比为1∶0.75，2～3级坡坡比为1∶1。

2)K50+600～K50+675右边坡(简称B边坡)，2级坡，边坡覆盖层较薄，基岩为强风化砂质板岩，呈灰黄色，岩石结构构造可见，岩石呈砂状及块状。边坡1级坡坡比为1∶0.5，2级坡坡比为1∶0.75。

3.2 有限元模型分析

利用有限元分析软件MIDAS NX建立了边坡的初始有限元模型(见图2)，考虑到初始强度参数要进行一系列折减，因此初始值的选取尽量大于真实强度参数取值，初始材料参数如表1所示，其中A边坡岩体采用中风化板岩参数，B边坡岩体采用强风化板岩参数。仅对粘聚力和内摩擦角进行折减，忽略坡面的框架防护结构，具体建模过程在此不做详述。

对整个模型首先进行地应力平衡，然后去除开挖部分单元，再计算开挖后边坡的位移。为了使拟合结果更好地反映边坡整体变形的演变过程，在边坡稳定的前提下进行了8次抗剪强度参数折减，然后选择如图2所示的5个节点提取位移数据，作为反分析的依据。

a) A边坡

b) B边坡

本文中强度折减法仅对模型上部的砂质板岩进行强度折减，强度折减系数与抗剪强度参数对应关系如表2、表3所示。

表1 初始材料参数材料重度/kN·m-3 泊松比弹性模量/MPa粘聚力/kPa内摩擦角/(°)强风化砂质板岩23.00.3580.0100.045.0中风化砂质板岩24.50.35200.0210.0100.0地基20.00.3860.080.035.0

表2 A边坡在不同折减系数下的抗剪强度参数折减系数粘聚力/kPa内摩擦角/(°)1.4150.0071.431.6131.2562.501.8116.6755.562.0105.0050.002.295.4545.452.487.5041.672.680.7738.462.875.0035.71

表3 B边坡在不同折减系数下的抗剪强度参数折减系数粘聚力/kPa内摩擦角/(°)1.190.9140.911.376.9234.621.566.6730.001.758.8226.471.952.6323.682.147.6221.432.343.4819.572.540.0018.00

3.3 位移-折减系数曲线

根据表2和表3中的数据设置有限元模型材料参数，对2个边坡分别进行8组折减系数下的有限元分析，提取5个节点(如图2所示)监测开挖后的位移，得到节点位移-强度折减系数曲线如图3和图4所示。

从图3和图4可以看出，各个节点的位移随着折减系数上升，首先缓慢增加，而后增加速率越来越大，此趋势对边坡下部的节点更加明显。采用了多种函数对2个边坡的节点位移di-强度折减系数Fa关系进行了拟合，要求R2达到0.95以上，结果发现对于边坡下部节点，采用4次多项式函数的拟合效果较好，而对于上部节点，采用3次多项式函数即可达到较好的拟合效果，表4显示了对A边坡5个节点的拟合情况。

图3 A边坡的节点位移-强度折减系数曲线

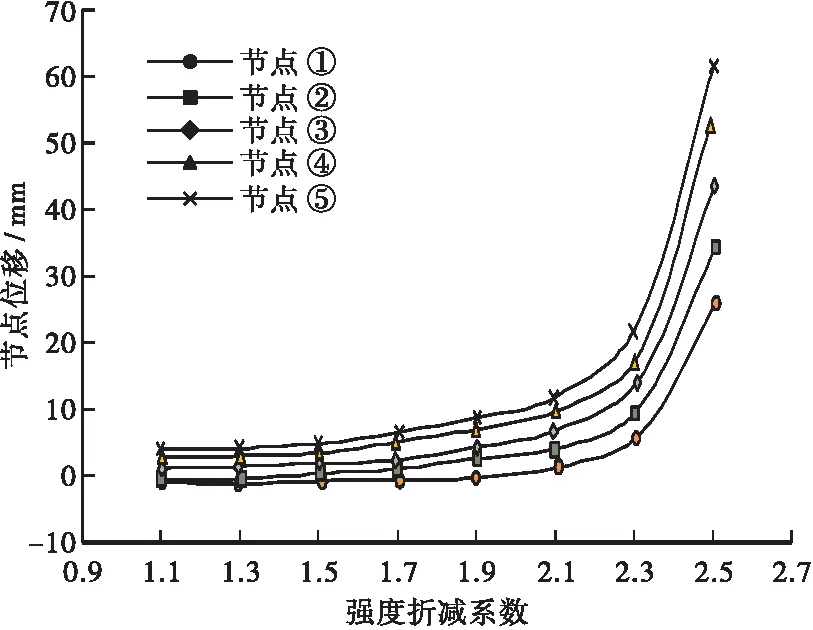
图4 B边坡的节点位移-强度折减系数曲线

表4 A边坡5个节点的位移—折减系数拟合情况节点号拟合函数R2①d1=6.544 9 F3a-35.727 F2a+64.695 Fa-39.5210.965 5②d2=9.663 1 F3a-53.219 F2a+98.453 Fa-60.1450.977 8③d3=12.603 F3a-68.445 F2a+125.14 Fa-74.4340.954 7④d4=31.024 F4a-239.11 F3a+685.83 F2a-862.06 Fa+402.210.969 7⑤d5=44.494 F4a-342.71 F3a+981.64 F2a-1 233 Fa+576.230.988 7

3.4 利用模拟退火法对折减系数进行寻优

以图2中各个位置开挖后的表面监测位移为依据，进行参数反分析，验证利用模拟退火法对折减系数进行寻优的可靠性。其中监测数据来自对于观测桩的定期观测，观测桩位于提取数据的节点处，开挖后进行位移观测，直至位移趋于稳定，认为所发生的位移为开挖引起的位移。A边坡和B边坡5个节点的监测位移如表5所示。

表5 2个边坡的位移监测值 mm边坡①②③④⑤A0.3473.215.817.439.23B-0.7350.4361.783.614.97

建立如式(4)的目标函数C，为使C达到最小值，利用MATLAB软件编写模拟退火法程序进行Fa的全局化寻优，该程序的流程图如图5所示。

图5 模拟退火程序流程图

(4)

式中：dmi为节点i的位移监测值；di为节点i的位移计算值。

对于最优强度折减系数的搜索过程如图6所示，最终得到2个边坡的反分析最优强度折减系数分别为2.38和1.55；将初始的抗剪强度参数除以折减系数，则得到A边坡的反分析抗剪强度参数为88.24 kPa(c)和42.02°(φ)，B边坡的反分析抗剪强度参数为64.5 kPa(c)和29.03°(φ)。将反分析抗剪强度参数代入有限元模型中，再次计算5个节点的位移，并与监测值进行对比(见图7和图8)，可以看出，5个节点的数据点都比较靠近斜率为1的虚线段(监测位移=计算位移)，这表明利用反分析抗剪强度参数计算得出的位移可以较为准确地反映监测位移情况。

图6 对于最优强度折减系数的搜索

图7 A边坡位移对比

图8 B边坡计算对比

4 结论

1)准确确定公路边坡岩体的抗剪强度参数对边坡设计具有重要意义。本文将模拟退火法(SA)引入到边坡岩体抗剪强度参数反分析中，根据计算数据和监测数据设定目标函数，编写模拟退火法寻优程序，搜索获取最优的强度折减系数，再进一步得出反分析抗剪强度参数。

2)针对所述方法开展了2处边坡的工程案例研究，将采用模拟退火法反分析得出的抗剪强度参数代入有限元模型中进行计算，各个节点的计算位移都比较接近监测位移，从而在一定程度上验证了该方法的可靠性和有效性。