FPSO火炬塔风激振动与数值计算方法研究

严锋 陈正豪 黄涣青

摘 要：本文以300 000 DWT级FPSO火炬塔设计为例，研究了在风场中火矩塔结构的风激振动。通过对风激振动下火矩塔的规范设计方法与ANSYS-CFX双向流固耦合数值计算方法研究，探讨了数值计算方法在工程中的实际应用。

关键词：FPSO;火矩塔;风激振动;双向流固耦合

中图分类号：U661.4

文献标识码：A

1 概述

结构风效应可以分为静力效应和动力效应：当结构刚度较大时，静力作用占主导作用，风振影响很小，一般把风能低频部分一平均风作用和高频部分一脉动风作用统一以平均风载荷乘以阵风系数来考虑;当结构刚度较小时，动力作用起主导作风，结构会发生强迫力下的抖振和涡振或白激力下的颤振和驰振，在进行准静态强度分析时，风振影响可用风振系数来表达。

FPSO火矩塔作为大跨度的结构，在海洋环境下，需要考虑其结构的动力效应，动力效应主要由涡激振动产生：当风流过火炬塔杆件时，会在杆件背风面形成交替脱落的漩涡（以下简称涡泄），从而在杆件断面上产生顺流向及横流向周期性变化的脉动压力，如果杆件为柔性的，则杆件会产生周期振动，即涡激振动。

在某个临界风速下，涡泄频率可能与结构的固有频率或其倍数接近，导致谐波或次谐波共振，从而产生强度破坏。火炬塔在设计时，应尽量避免杆件出现涡激振动，对于无法避免涡激振动的杆件，应采取相应的措施来消除涡激振动对杆件的影响。

2 涡激振动的研究方法

传统的对涡激现象的研究，可分为四种方法：理论模型法;风洞实验法;现场实测法;数值模拟法。众多学者在对涡激振动现象进行了大量试验研究的基础上，建立了各种数学模型，通过求解这些数学模型解析解来研究涡激振动。如升力振子模型、经验线性模型、经验非线性模型、通用经验非线性模型[1]等。但解析求解过程非常复杂，很多情况下很难求得解析解，而实验方法与现场实测费时费力，因此工程上常采用经验规范方法和直接数值模拟计算方法。

对FPSO火炬塔而言，DNV环境与载荷规范提出了对涡激振动的衡准。同时，随着计算机技术的发展，一些精确的数值模拟方法也被应用于涡激振动预报与控制。

早期的涡激振动数值计算方法仅利用一个流体软件来实现，其核心思想是基于弹性支撑的刚体二维模拟，流体与结构的耦合作用利用动网格技术来实现，结构的运动响应被离散成流体的边界条件。这种方法对理论知识水平和计算机编程技术要求很高，只适用于特性情况特定解法，并且忽略了杆件的三维尺度效应[2]。

流固耦合数值计算软件主要有Ansys+CFX、Fluent+Ahaqus、Adina、COMSOL Multiphysics（FEMLAB），目前Ansys又推出了AnsV s+CFX/Fluent+system-coulping等模块，整体来说无论理论还是方法都越趋成熟。

3 涡激振动的规范计算方法

风引起管件发生周期激振，可能发生在沿风向或与管件垂直的横向位置，使结构杆件产生较大的位移及变形，造成杆件局部的破坏甚至火矩塔整体破坏。目前的设计思想是使结构基频避开涡激振动频率，规范大都采用此原理。海洋工程中广泛使用DNV-RP-C205环境和载荷规范[3]的方法来进行涡激振动计算。

本文以FPSO火矩塔为研究对像，分析时取极端条件下该高度处的一分钟平均风速;对于制造和运输分析，采用10年一遇该高度处的一分钟平均风速。结构模型如图1所示。

根据此标准进行计算，结果表明：

除横杆C005- B005等个别杆件外，大多数火炬塔避开了涡激振动区域;对不满足规范要求的结构进行重新设计，通过增加一个支撑以减少杆件长度，可使结构满足规范要求。

4 三维涡激振动仿真计算

规范设计只能判断涡激振动是否可能发生，而不能判断涡激振动对火矩塔结构的具体影响。随着计算机硬件水平的提高和数值计算方法的发展，三维模拟可以更真实的判断出涡激振动的影响，指导结构进行优化设计。

结构在流体作用力下会发生运动和变形而产生振动，这种振动会加剧漩涡的释放，反过来涡的释放又会加剧结构的振动[5]。但在现实中涡激振动幅值是有限的，当某时间步内流体一结构一流体这一循环求解过程满足迭代标准时，就可以认为其过程是收敛的，因此数值求解流体和结构相互影响的方法是可行的。

本文以超出规范限制的一根火炬塔杆件为研究对象，探讨双向流固耦合计算方法。该计算杆件尺为：直径D=0.219 1 m; t=0.012 7 m;杆件长L= 10 m;风速U= 20 m/s。根据DNV规范计算结果，该杆件的Vr=6.63、Ks=13.67，可能发生横向振动。

4.1 杆件固有频率计算

结构的固有频率，可通过一般有限元方法求得。根据计算结果，此结构模型固有频率为25 Hz。

4.2 圆柱绕流数值仿真计算

在计算涡激振动频率之前，要先进行静态绕流计算，确定涡泄频率与Strouhal数。St值取决于构件型状与雷诺数。

在亚临界区（300

计算流场采用Icem画分，总网格数约为23万个。计算采用了RANS k-ε方法，壁面网格Y+=30，计算精度在工程上是可以接受的。

流场左侧为速度入口，右侧为自由出流;上下边界为无滑移固壁边界;顶面与底边为对称边界;模型上游为5D，下游为25D;上下边界离网柱中心为5D。研究表明，该流场大小可以忽略流场边界的影响。

数值计算中，采用了有限体积法。其中，对流项采用二阶迎风差分格式，压力和速度的耦合采用SMPLEC算法。流体计算域网格，如图2所示。

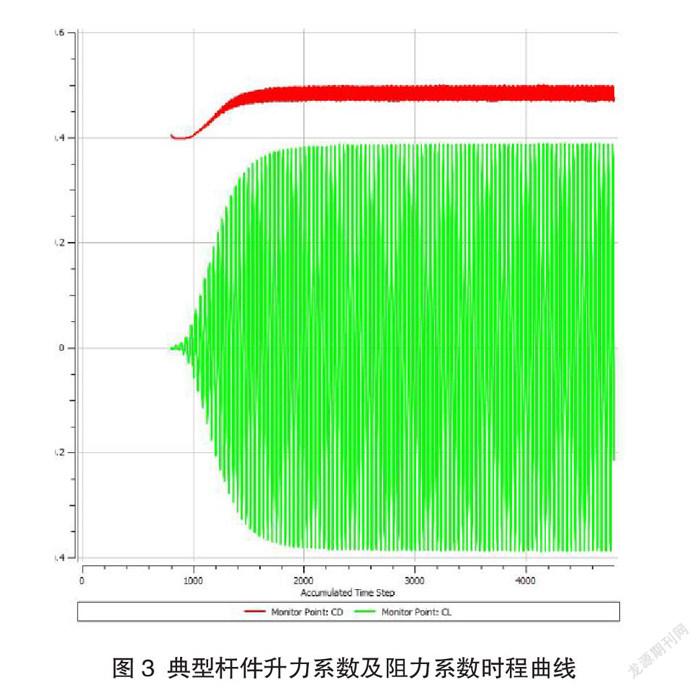
当风速U= 20 m/s時，涡脱频率为25.5 Hz。此时，雷诺数Re= 2.9+e5，处于临界流范围，相应的St=0.279;杆件升力系数及阻力系数时程曲线，如图3所示。静态绕流表明，风经过杆件时，产生了交替发生的尾涡，

4.3 三维涡激振动流固耦合计算

本文采用CFX和Ansys transit模块进行流固耦合计算，采用顺序耦合方式和动网格技术，参考前文圆柱绕流分析的结果，对某构件进行了单独的涡激振动数值计算。

由三维静态绕流计算可知，当风速U= 20 m/s时，涡脱频率fs= 25.5 Hz与物体的固有频率fn接近，此风速即为开始涡激振动的起振风速。在此风速下，进行三维杆件涡激振动仿真计算。

计算杆件横向位移曲线，如图4所示。从图4可以看出，3s后流动稳定，涡激振动也变得稳定。通过FFT变化，共振频率为25.29 Hz，如图5所示。6s时，杆件位移与应力如图6、图7所示。

由图6、图7可知，虽然产生了涡激振动，但是应力并不大，没有直接破壞杆件。

6s时流场的速度云图、压力动图如图8、图9所示。

由图8、图9可以看到，风经过杆件时，产生了交替脱落的涡，因此产生涡激力，并且在三维方向流动并不一致。

5 结论

本文通过对火炬塔涡激振动进行规范计算与数值计算，发现：规范计算是比较保守的，在产生涡激振动现象时，杆件并不一定会发生破坏。数值计算虽然计算较之精确，但计算周期长。因此，先采用规范进行定性计算，筛选出典型构件，再视情况进行定量计算比较合理。在本文的研究中，没有考虑其它杆件的遮蔽效应，仅研究了单根杆件，今后以整体为研究对像是三维数值研究发展的趋势。

参考文献

[1]葛耀君.大跨度悬索桥抗风[M].北京：人民交通H{版社.2011.

[2]方媛嫒.三维圆柱体绕流数值模拟流场选对及网格划分[J]水道港口，2009，vol30（ Nol）：70-76.

[3]李峰.输电塔典型节点钢管杆件涡激振动研究[D]上海：同济大学.2008

[4]詹吴.钢桁拱桥吊杆涡激振动仿真分析[D].武汉：华中科技大学.2009.

[5] RP-C205 Envuorunental conditinns and envirnnmental loads[S].Norwav：DNV.2007

[6]海洋石油T：程设计指南编委会.海洋石油工程平台结构设计第4册[M].北京：石油工业出版社.2007： 53-54.

[7]任大朋.一种基于ANSYS和FLUENT的海洋立管的涡激响应分析方法[J]中国海洋平台，2007（ 04）：32-36.