基于不同循环基本组织的铺砌织物组织设计

郝梓淇 金耀

摘要： 为扩展织物组织的设计思路，提供更多富于变化、风格独特的织物组织，受到瓷砖铺砌的启发，文章运用瓷砖铺砌的思路提出一种新的铺砌织物组织设计方法。该方法运用循环数不同的2种基本组织按周期铺砌规则生成织物组织。首先采用图数据结构表示瓷砖铺砌结构;然后由小铺砌块为根节点层次遍历图结构构造一棵生成树形成铺砌结构，并根据组织的四方连续性要求裁剪铺砌结构;最后按遍历顺序依次将基本组织填充至树的节点。运用C++编程语言实现了该方法并进行了多种不同变化形式的仿真设计实验。结果表明：该织物组织设计方法灵活便捷且变化形式多样，所生成的织物组织结构多变，且具有周期对称、错落有致等传统组织所不具有的特点。

关键词： 瓷砖铺砌;织物组织设计;基本循环;生成树;数据结构

中图分类号： TS105.11

文献标志码： A

文章编号： 1001-7003（2021）09-0133-06

引用页码： 091303

DOI： 10.3969/j.issn.1001-7003.2021.09.020（篇序）

Tilingbased fabric weave design with fundamental weaves of different repeats

HAO Ziqi， JIN Yao

（School of Information Science and Technology， Zhejiang SciTech University， Hangzhou 310018， China）

Abstract： To enrich the design ideas of fabric weaves，and provide more diversified and unique fabric weaves， a new tilingbased fabric weave deign method inspired by floor tilings is proposed. It adopts two fundamental fabric weaves with different repeats to generate new fabric weaves according to periodic tiling rule. The floortiling structure is represented as graph data structure firstly. Then， the tiling structure is built with the help of the spanning tree， which is constructed by the BFS traversal of the graph and is clipped according to the consecutive foursquare principal of fabric weaves. Finally， fundamental weaves are filled into the nodes of the tree in the traversal order. The proposed method is implemented with C++ programming language and several simulation experiments are performed with different parameter controls. The results show that the fabric weave design method is convenient， flexible， and can change variably in design. And the designed fabric weaves are rich in variable structures， and embodies features of periodic symmetry and wellarranged tilings， which are not shared by traditional weaves.

Key words： floor tilings; fabric weave design; fundamental weave; spanning tree; data structure

收稿日期： 20210321;

修回日期： 20210818

基金項目： 国家创新训练项目（202110338021）;国家自然科学基金项目（61702458）;绍兴市技术创新计划（揭榜挂帅）项目（2020B41006）

作者简介： 郝梓淇（2000），男，2018级智能科学与技术专业本科生。通信作者：金耀，副教授，jinyao@zstu.edu.cn。

机织物经纬纱线的交织方式与沉浮规律通常运用织物组织表示[1]。织物组织的变化形式不仅影响织物的结构性能，而且直接影响织物的外观[2-3]，是研究和开发新产品的重要手段[4]。因而织物组织设计一直是纺织品设计中的一个常规而重要的研究课题。

为了丰富织物组织的变化形式，同时提高织物组织的设计效率，研究者利用经典的数学工具建立了各种组织表达与设计模型，并借助计算机技术实现高效的数字化设计，例如几何模型[5-6]、矩阵模型[7]、图像模型[8]、代数群模型[9]、分形模型[10]等。几何模型通常利用几何对称性，例如旋转、平移、反射等对局部组织进行变换重组，设计具有对称结构特点的组织。矩阵与图像模型，则运用矩阵与图像表示织物组织，对已有的织物组织施加某种变换生成新的组织，这两类设计方法的变形形式往往较为单调。代数群模型从代数观点对织物组织进行建模，使织物组织间能够像代数一样进行灵活运算，但其应用研究的讨论较少。分形模型则借助分形几何原理，利用分形的自相似性特点，将单个组织循环作为几何单元进行层次嵌套变化，能够生成复杂多样、风格特异的织物组织。这种分形织物组织设计方法随后得到了迅速发展，在生成方法、变化形式等方面出现了各种各样的变种，如基于IFS[11]、各层基础组织互异[12]、基于同层仿射变换[13]、基于斜纹基本组织设计方法[14]，以及更为一般的扩展分形模型[15]等。

2020年，金耀等[16]借助铺砌理论，从构造织物组织空间布局的角度提出了基于椅子铺砌的设计方法。该方法利用1个铺砌块组织作为基础组织，在预设的铺砌结构下进行变换平铺，所设计的织物组织风格新颖，既具备分形织物组织的一些特点，又具有结构独有的局部对称性。无论是分形组织还是椅子铺砌织物组织，它们均由1个或多个同组织循环数的基础组织经过平移铺砌而成。本文受到瓷砖铺砌构图的启发，尝试用2种不同循环数的基础组织，对平面空间进行错落有致地铺砌重构，变化更为灵活自由，可实现由简单基础组织形成复杂多变、风格新颖的铺砌织物组织。

1瓷砖铺砌

1.1铺砌的概念

铺砌已被人们广泛运用于图案设计[17]及日常生产与生活中，如图1所示为各种不同铺砌块所形成的地砖铺砌效果[18]，让人赏心悦目。

如文献[14-15]所述，通常可运用集合语言描述这种能够无空隙且不重叠覆盖平面空间的“铺砌”，由多个铺砌块（基本几何单元）所构成的集合，且满足如下条件：1） 集合中每个铺砌块是一个闭集;2） 所有铺砌块的并集铺满二维欧式平面;3） 任意2个铺砌块内部的交集为空。

1.2基于不同单元的瓷砖铺砌及生成方法

图1中，瓷砖铺砌的形式丰富多样，其中不乏各种基于不规则几何形状的铺砌形式。本文选定一种特殊的瓷砖铺砌形式，即图1右上角由2种不同尺寸的正方形作为铺砌块（分别称为大铺砌块与小铺砌块，统称“基本组织”）形成的周期铺砌结构。该铺砌与织物组织天然具有的矩形结构相吻合，因此适用于织物组织设计。本文则着重讨论如何利用该铺砌结构进行织物组织设计，所设计的组织称为“瓷砖铺砌织物组织”。

这种形式的瓷砖铺砌可由2个大小方形铺砌块（图2（a））拼合成图2（b）所示的基本铺砌单元，将其作为新的铺砌块，经过平移对称变换铺满整个平面。为了增加组织的空间变化形式，本文以1个小铺砌块和4个大铺砌块按图2（c）所示进行拼合，由此所形成的图形作为基本铺砌单元。该基本单元具有中心对称性，在进行组织设计时，可对4个大铺砌块进行几何变换，易于织物组织的变化设计。

但是严格来讲，图2（c）所示基本铺砌单元不构成铺砌块，即不能无重叠地铺满平面空间。为此，本文放宽铺砌条件，对其进行“局部可重叠”地铺砌，当待铺砌的基本铺砌单元与平面上已有铺砌块重叠时，则隐藏该基本铺砌单元的重叠铺砌块。为了方便基于该基本铺砌单元存储并生成该瓷砖铺砌结构，本文利用铺砌单元的中心对称性，采用“图”描述铺砌结构G=〈V，E〉：顶点集V表示大铺砌块和小铺砌块集合，边集E表示两个铺砌块的相邻关系，即若两者相邻则存在边e∈E（图3（a））。该瓷砖铺砌结构具有规则的拓扑连接关系：1） 每个小铺砌块均连接4个大铺砌块，每个大铺砌块均连接4个小铺砌块与4个大铺砌块;2） 与每个铺砌块连接的其他铺砌块均分别位于该铺砌块4条边的上下左右方位;3） 小铺砌块之间不直接相连。这种特殊的固定拓扑结构能够简化铺砌结构及铺砌织物组织的描述。

为了生成这种铺砌结构，本文利用铺砌结构所表示的图的“生成树”进行构造式生成：以位于中心的小铺砌块为生成树的根节点，按广度优先顺序层次遍历图的节点。即对于当前节点（铺砌块），依次遍历它的邻域节点（铺砌块），若该邻域节点未曾被访问则将两个節点加上边（节点相邻），否则不加边（节点已被访问），如此循环直到遍历预设的层次数停止。图3（b）所示是层次遍历2层后得到的生成树，其遍历1层与遍历2层得到的结果对应于图4（a）（b）左侧的铺砌结构图，由于其形状不呈方形，因此可通过裁剪获得矩形区域，作为铺砌织物组织的框架，如图4（a）（b）右侧所示。

2基于瓷砖铺砌的织物组织设计

2.1瓷砖铺砌织物组织设计方法

类似于椅子铺砌织物组织设计方法[16]，利用瓷砖铺砌进行织物组织设计同样遵循如下设计步骤：1） 构造铺砌结构;2） 设计铺砌块组织;3） 生成铺砌织物组织。所不同的是本文提出的基于瓷砖铺砌的设计方法需提供2个铺砌块组织，并且给出了更多的设计参数。

在实际应用中，织物组织通常需具备四方连续性，使组织在平铺过程中保持自然过渡。本文研究发现，对瓷砖铺砌织物组织进行裁剪时，若其组织循环数满足m2+n2的整数倍时（其中m、n分别是大小基本组织的循环数），则该铺砌织物组织满足四方连续性。该性质可简要证明如下：大基本组织有m种纬向交织形式，分别设为A1，A2，…，Am，而小基本组织有n种纬向交织形式，分别设为B1，B2，…，Bn;根据瓷砖铺砌的铺砌结构规律，其第1条纬向交织形式依次由大小基本组织按某种顺序排列，如A1B1A2B2，…，Am，其后的纬向交织形式可依次将队首的两个字母挪至队尾生成;如第2条纬向交织形式为A2B2，…，AmA1B1，如此规律可获得整个组织所有的纬向交织形式，即最小循环数的铺砌织物组织，如图5所示的红色线框;因此，其循环数为m2+n2的倍数。图5所示基本铺砌单元中，m=3，n=2，则红色线框的左侧部分可为一个循环内的一条经纱，即其组织循环数最少为13。

此外，根据组织工艺要求，组织经循环数不能超过内经纹针数或是内经纹针数的约数。因此在实际应用中，可根据内经纹针数选取符合循环数约数要求的大小基本组织，或者扩大铺砌织物组织的经循环数，使经循环数等于内经纹针数。

图6展示了瓷砖铺砌织物组织的设计过程。在该设计步骤中，前2步由用户输入设计意图，根据织物组织的四方连续约束分别确定织物组织的空间结构与局部铺砌形式，第3步由计算机程序自动完成。其中，铺砌结构的构造由输入的2个基本组织的循环数及生成树的深度确定，组织的结构可由确定循环数的组织外形（矩形）与铺砌结构裁剪而成。2个铺砌块组织可选用符合组织工艺要求的组织，如常见的平纹组织、斜纹组织、缎纹组织等三原组织或其他复杂组织。得益于基本组织的循环数不同可错落排列，亦可选择使生成铺砌织物组织满足组织工艺要求，但经纱或纬纱没有交织点的“不合理”的组织。

2.2瓷砖铺砌织物组织的变化设计

相比于椅子铺砌织物组织[16]，本文所提出的瓷砖铺砌织物组织设计方法由于采用了2种组织循环、类型不同的基本组织，进行错落有致地空间铺排，其设计自由度更大，变化形式更为多样，并主要从基本组织的循环数、类型、几何变换等方面对织物组织进行创新设计。

1） 基本组织的类型。对于确定铺砌结构及固定循环数的2个基本组织，进行基本组织的类型变化将最大程度地改变铺砌织物组织的外观。

2） 基本组织的循环数。设大小基本组织的循环数分别是R与r，则两者满足关系：R>r>0。通过调整大小基本组织循环数值R与r，将对整体铺砌结构带来变化，从而形成不同的铺砌织物组织效果。

3） 基本组织的几何变换。本文所采用的瓷砖铺砌结构，从局部来看，由4个大基本组织环绕1个小基本组织（图2（c）），因此通过对4个大基本组织施加不同的旋转变换，可生成不同的铺砌织物组织。图7（a）中，大铺砌块内的数字代表旋转，数字0～3分别表示对大铺砌块组织执行90°旋转的次数，即分别为：{R0，R1，R2，R3}。在构造生成树时，仅需将树的子节点依次编号即可，使小基本组织的四个邻接大基本组织的数字编号互异，如图7（b）所示。

3仿真实验与讨论

本文运用C++语言实现上述瓷砖铺砌织物组织设计方法，并采用QT库对所生成的织物组织意匠图进行可视化仿真，进一步讨论各种不同变化形式对织物组织设计效果的影响。

3.1基本组织形式的变化

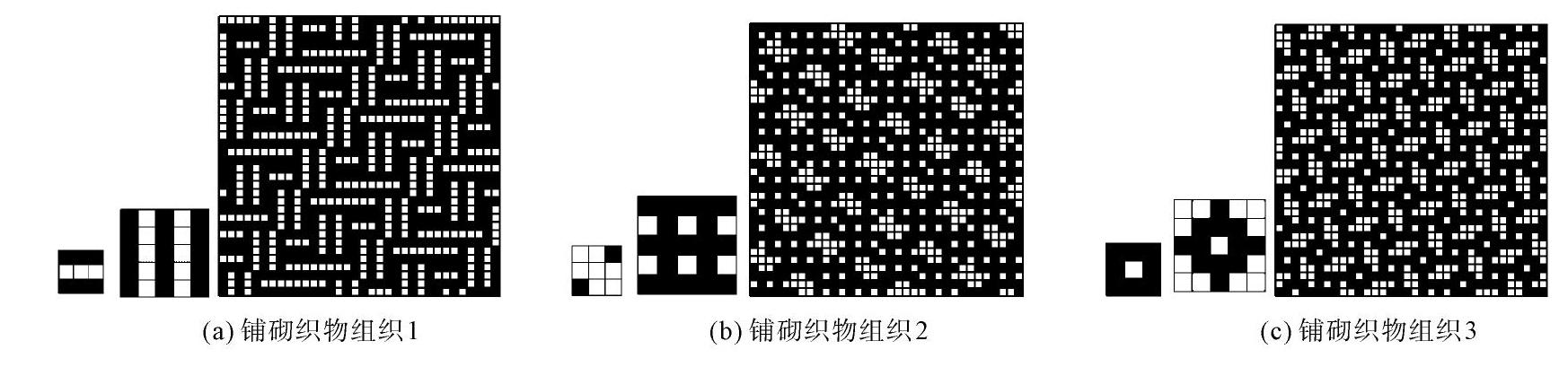
改变基本组织的形式能够最大程度地改变铺砌织物组织的外观，因而通过设计不同的铺砌块组织可获得更多的瓷砖铺砌织物组织。图8为采用不同的铺砌块组织设计的铺砌织物组织，其大小基本组织见于各组图的左下角，对应的铺砌结构同图6（a）。由图8可见，不同的铺砌块组织所生成的瓷砖铺砌织物组织外观效果差异较大，风格各不相同。

3.2基本组织循环数的变化

铺砌织物组织由2种不同循环数的基本组织生成，可通过调整基本组织的循环数改变组织外观。对于给定的2个基本组织，在保持大铺砌块组织不变，而仅改变小铺砌块组织的循环数时，所生成的铺砌织物组织虽然在整体上仍具有一定的相似性，但其局部产生了扰动变化，形成了新的组织，如图9所示。

3.3基本组织的空间旋转变化

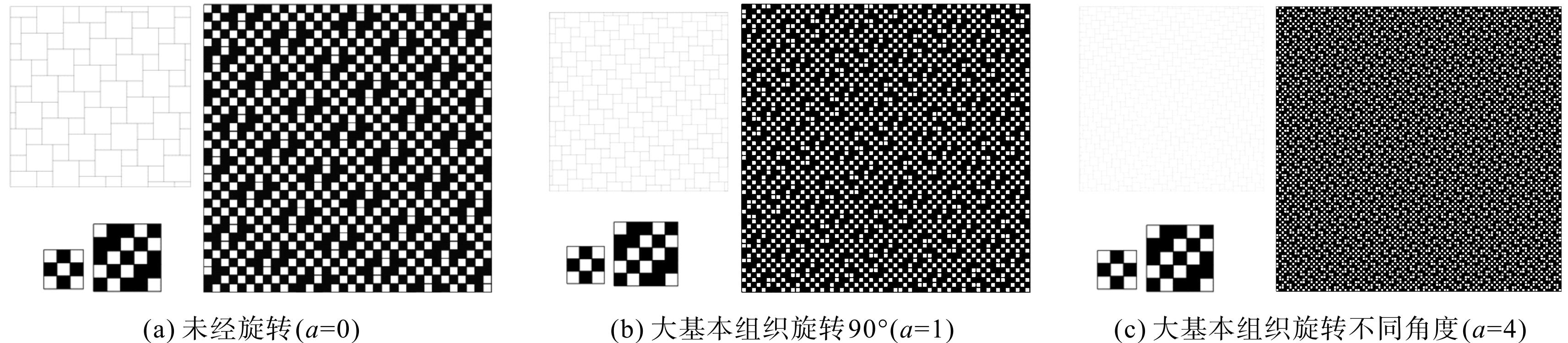
由于本文瓷砖铺砌的基本铺砌单元具有中心对称性，即1个小铺砌块被4个大铺砌块围绕。因此，通过对小铺砌块或者4个大铺砌块进行局部旋转变换也将生成新的组织。但施加旋转变换过后，4个大铺砌块中会有a个大铺砌块会发生变化，大基本组织有（a+1）m种纬向交织形式，此时所得到的织物组织将破坏四方连续性。类似2.1节的证明可知，当循环数为（a+1）m2+n2的整数倍时，该铺砌织物组织满足四方连续性。为此，本文根据大铺砌块发生旋转变换的数目a，对施加旋转变换后铺砌织物组织的循环数进行扩增。如图10所示，保持小铺砌块组织不变，而对大铺砌块组织采用不同的旋转变换得到了不同的铺砌织物组织。其中图10（a）未经旋转变换，图10（b）对所有大基本组织旋转了90°，而图10（c）则采用了图7（a）的互异旋转变换。

3.4任意“基本组织”形式

与分形组织及椅子铺砌织物组织不同，本文的瓷砖铺砌织物组织对基本组织的限制较松，不严格要求基本组织要符合工艺要求，即经纱或纬纱必须交织至少1次。如图11所示，由一些不符合实际工艺要求的基本组织相互配合进行铺砌，将生成一些具有特殊效果的织物组织，所形成的铺砌织物组织呈现各种别样的小花型，如阶梯状、风车状等花型效果。

4结论

由计算机仿真实验表明，本文基于瓷砖铺砌方法，利用2种不同基本组织生成织物组织的设计方法是可行的。该方法在织物组织四方连续性约束下利用图数据结构运用生成树的构造过程生成铺砌结构，并将2种不同的基本组织在铺砌结构的相应位置进行填充，最终形成铺砌织物组织。该方法的组织变化形式多样，所生成的织物组织独具一格。该方法在椅子铺砌织物组织的基础上，进一步探索了铺砌理论在组织设计的应用，开拓出不同的织物组织设计空间。未来将挖掘更多的可用于织物组织设计且风格新颖的铺砌结构，并研究建立设计铺砌织物组织的一般理论与方法。

PDF下载

参考文献：

[1]顾平. 关于织物组织设计的理念更新[J]. 丝绸， 2005（7）： 18-20.

GU Ping. Study on idea renewal in fabric weave design[J]. Journal of Silk， 2005（7）： 18-20.

[2]张袆， 王美玲， 何小祎， 等. 织物组织结构对装饰用桌布性能的影响[J]. 纺织科技进展， 2020（11）： 22-25.

ZHANG Hui， WANG Meiling， HE Xiaoyi， et al. Effect of fabric structure on properties of decorative tablecloth[J]. Progress of Textile Science and Technology， 2020（11）： 22-25.

[3]刘沐黎， 袁理， 杨亚莉， 等. 色纺机织物组织结构对其呈色特性的影響[J]. 纺织学报， 2020， 41（9）： 45-53.

LIU Muli， YUAN Li， YANG Yali， et al. Effect of fabric structure on color rendering characteristics of color spun fabrics[J]. Journal of Textile Research， 2020， 41（9）： 45-53.

[4]陈敏， 罗炳金. 提花真丝领带织物组织设计与实践[J]. 纺织导报， 2018（7）： 65-68.

CHEN Min， LUO Bingjin. Weave design and practice of jacquard silk tie fabric[J]. Textile Guide， 2018（7）： 65-68.

[5]施国生， 胡觉亮. 对称性原理在织物组织设计中的应用[J]. 浙江工程学院学报， 2000（3）： 155-157.

SHI Guosheng， HU Jueliang. Symmetrical principle applied to fabric weave design[J]. Journal of Zhejiang Institute of Science and Technology， 2000（3）： 155-157.

[6]赵良臣， 闻涛. 旋转组织设计的数学原理[J]. 纺织学报， 2003， 24（6）： 33-34.

ZHAO Liangchen， WEN Tao. The mathematical principle of rotational weave design[J]. Journal of Textile Research， 2003， 24（6）： 33-34.

[7]施国生， 梁道雷. 多臂织物组织矩阵的自动设计[J]. 纺织学报， 2002， 23（6）： 60-61.

SHI Guosheng， LIANG Daolei. Automatic design of multiarm fabric weave matrix[J]. Journal of Textile Research， 2002， 23（6）： 60-61.

[8]施国生， 张瑜秋， 熊超. 图像变换在多臂织物组织设计上的应用[J]. 纺织学报， 2006， 27（7）： 23-26.

SHI Guosheng， ZHANG Yuqiu， XIONG Chao. Application of image transformation technique on dobby fabric weave design[J]. Journal of Textile Research， 2006， 27（7）： 23-26.

[9]金耀， 张聿. 织物组织的群表达方法[J]. 纺织学报， 2010， 31（6）： 48-51.

JIN Yao， ZHANG Yu. Studies on fabric weave representation by group theory[J]. Journal of Textile Research， 2010， 31（6）： 48-51.

[10]张聿， 金耀， 孙家武， 等. 基于L系统的织物分形组织设计方法[J]. 纺织学报， 2007， 28（5）： 51-54.

ZHANG Yu， JIN Yao， SUN Jiawu， et al. Design method of fabric fractal weave based on Lsystem[J]. Journal of Textile Research， 2007， 28（5）： 51-54.

[11]張聿， 金耀， 岑科军. 基于IFS的非规则分形组织设计方法[J]. 纺织学报， 2012， 33（12）： 30-34.

ZHANG Yu， JIN Yao， CEN Kejun. Method of designing irregular fractal weave based on IFS[J]. Journal of Textile Research， 2012， 33（12）： 30-34.

[12]马铃琳， 张聿. 各层基础组织互异的分形组织设计方法[J]. 丝绸， 2013， 50（9）： 45-49.

MA Linglin， ZHANG Yu. Design method of fractal weave with diverse basic weaves in different layers[J]. Journal of Silk， 2013， 50（9）： 45-49.

[13]熊丽丽， 张聿. 基于斜纹基本组织的回纹分形组织设计方法[J]. 丝绸， 2015， 52（1）： 31-34.

XIONG Lili， ZHANG Yu. Design method of fret fractal weave based on twill weave[J]. Journal of Silk， 2015， 52（1）： 31-34.

[14]章平， 张聿. 同层仿射分形织物的设计方法[J]. 丝绸， 2014， 51（12）： 3538.

ZHANG Ping， ZHANG Yu. Design method of fractal fabrics of affinity in the same layer[J]. Journal of Silk， 2014， 51（12） 35-38.

[15]熊宇龙， 张华熊， 鲁佳亮， 等. 基于扩展分形模型的织物组织设计方法[J]. 浙江理工大学学报（自然科学版）， 2018， 39（3）： 341-345.

XIONG Yulong， ZHANG Huaxiong， LU Jialiang， et al. Fabricweave design method based on extended fractal model[J]. Journal of Zhejiang SciTech University（Natural Sciences Edition）， 2018， 39（3）： 341-345.

[16]金耀， 蔡腾皓， 李彩曼， 等. 基于椅子铺砌方法的织物组织设计[J]. 纺织学报， 2020， 41（9）： 54-58.

JIN Yao， CAI Tenghao， LI Caiman， et al. Application of chairtiling approach for fabric weave design[J]. Journal of Textile Research， 2020， 41（9）： 54-58.

[17]PEICHANG Ouyang， KWOK Waichung， ALAIN Nicolas， et al. Selfsimilar fractal drawings inspired by M. C. Eschers print square limit[J]. ACM Transactions on Graphics， 2021， 40（3）： 1-34.

[18]FATHAUER R. Tessellations： Mathematics， Art， and Recreation[M]. Natick： A K Peters/CRC Press， 2020： 89-100.