不锈钢折弯板裂纹Lamb波检测技术∗

胡晓丹 周世圆 赵明华 于全朋

(北京理工大学机械与车辆学院 先进加工技术国防重点学科实验室 北京 100081)

0 引言

不锈钢折弯板构件在工程中有非常重要的应用，例如容器壳体、飞机支撑零件、汽车钣金件等。工程中经常使用的油箱、水箱等薄壁容器，厚度在2～5 mm 之间，也可以看作是90°折弯的板状结构。在加工弯曲件的过程中，折弯处易形成应力集中从而引起裂纹缺陷。裂纹是折弯结构中一种典型缺陷，严重削弱了弯板的承载能力和抗腐蚀能力。尤其是在交变载荷的作用下，裂纹迅速扩展，造成弯板的断裂，对系统的正常运行构成了安全威胁［1]。因此，对不锈钢弯板折弯处进行缺陷检测是非常必要的。目前，对板中裂纹的无损检测方法有涡流、漏磁、声发射、红外、超声等［2−3]。相比之下，超声检测具有穿透能力强、灵敏度高、设备安全以及便于安装携带等优点［4]，因此在板结构的缺陷检测中具有良好的应用前景。

Lamb 波是一种在厚度和激励声波波长为相同数量级的声波导中由纵波和横波叠加而形成的特殊应力波，也被称为板波［5]。相比于传统的体波，Lamb 波传播时衰减小，传播距离长，检测效率高，而且可以在弯曲的被测件中传播。Lu 等［6]利用集成的有源压电传感器网络，实现对铝板上5 mm和20 mm 长的裂纹的检测和定位；An 等［7]采用对Lamb 波频率-波数域分析的方法，对板的焊接加强筋引起的裂纹进行识别和定位；Grondel 等［8]使用Lamb 波对铆接铝板中由疲劳载荷引起的接头裂缝进行检测和定位。Lamb 波对规则的平板结构的裂纹检测已经有大量的研究应用，而折弯板状结构中的裂纹检测的研究相对较少。

对于缺陷类型和尺寸的识别一直以来是超声检测领域的热点。小波包分析是对传统傅里叶分析的发展，根据信号特征选取可变的窗口，可以在时频域内对信号进行分析，尤其是可以同时分析信号的低频和高频部分，提供更全面的细节信息［9−10]。

本文将水箱等容器的折弯处结构简化为角度为90°的“L”形不锈钢折弯板，计算频散曲线，优选出模态并研究其在板结构中的传播特性。使用COMSOL 软件建立简化后的二维“L”形不锈钢板频域有限元模型，对Lamb 波的传播情况进行仿真计算。采用脉冲回波法进行实验验证，并且利用小波包变换(Wavelet packet transform,WPT)方法对回波信号进行分析，实现对裂纹缺陷的检测和识别。

1 Lamb波频散曲线计算及模态选择

频散性和多模态性是Lamb 波的典型特性［11]。对于不同的检测对象，需要对Lamb 波的频散特性进行分析来选择合适的模态进行检测。Lamb 波是在自由板中产生的平面应变波，板的上下表面应力为零［12]。在传播过程中，波在板的边界不断发生反射，这个过程中横波与纵波不断地发生转换。由于波之间存在相互干扰，进而形成了波包，即为不同模态的Lamb波。Rayleigh-Lamb频散方程［12]为

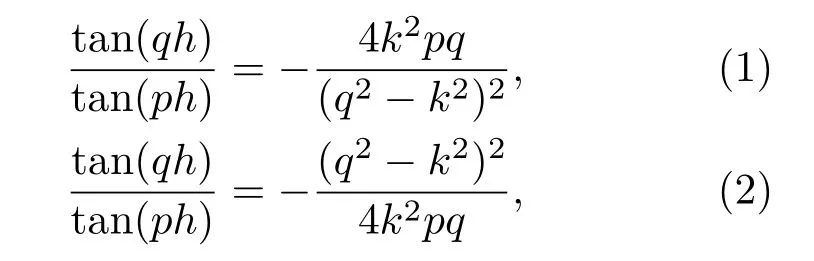
其中，p和q由式(3)给出：

其中，k为波数，ω为频率，h为板厚的一半，cL和cT分别为纵波和横波的波速。在波的传播过程中，波速是与传播介质的密度、泊松比等材料特性参数密切相关的。在不同的介质中传播将会有不同的波速，同样也将会有不同的频散特性曲线。

设置数值求解对象为201 不锈钢板，厚度为3 mm，纵波的传播速度cL=5900 m/s，横波的传播速度cT=3230 m/s，其材料特性参数见表1［13]。

表1 201 不锈钢材料特性参数Table 1 Material properties of the 201 stainless steel

求解Rayleigh-Lamb 频率方程，可以得到波数关于频率和传播速度的数值解。绘制频散曲线如图1所示。图1 中实线代表Sn，虚线代表An(n= 0,1,2,···)。选择合适模态的Lamb 波，可提高对钢板中的裂纹缺陷的检测灵敏度。由图1 可见，低频段具有模态数量少和频散小的优点，有利于激发出模态单一的Lamb 波进行研究。结合实验室现有的探头、斜楔等实验条件，以及激发出能量值高、稳定良好的信号，选择频率为0.25 MHz、0.5 MHz和1 MHz 的S0 模态进行研究。由于导波的检测能力与波长密切相关，波长随频率连续变化，故研究该3 个频率模态点，便可选出低频段S0 模态的敏感频段。

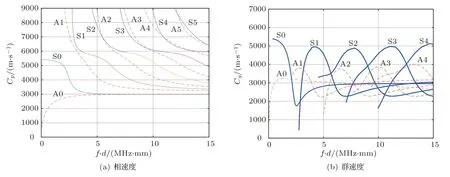
图1 钢板Lamb 波频散曲线Fig.1 Lamb wave dispersion curve of steel plate

2 Lamb波传播的频域有限元仿真

2.1 基于频域有限元法建立COMSOL仿真模型

工程中常使用数值分析方法对超声导波的传播过程进行有限元仿真，包括时域有限元法(Time domain finite element method,TDFE)和频域有限元法(Frequency domain finite element method,FDFE)。相比时域有限元法，频域有限元法计算效率更高，时间成本更低，且能够满足分析需求，故本文采用频域有限元法进行仿真建模。

线性弹性波导的控制方程［12]由式(4)～(6)所示，

其中，σ表示柯西应力，C表示弹性模量张量，ε是应变张量，u表示位移场，ρ表示材料的质量密度，∇符号代表全偏导算法。在频域中求解方程，假设在频率为ω情况下，位移，应力其中表示笛卡尔坐标下的波导介质上点的位置，得到新的线性动量平衡方程为

利用半解析有限元法求解等式(7)，可以得到指定频率下的位移场u(ˆs)。由于裂纹缺陷的存在对位移场有明显影响，可通过建立仿真模型，激励指定频率点Lamb波，计算有无缺陷的位移场变化情况，进而判断不同Lamb波的缺陷检测效果。

COMSOL 是一款应用于多物理场交叉学科的数值计算和复杂工程问题的仿真软件，以有限元法为基础，通过求解偏微分方程或偏微分方程组来实现真实物理现象的仿真，用数学方法求解真实世界的物理现象。选择固体力学模块中的频域求解器，建立二维仿真模型，如图2所示，材料特性参数依据表1设置。

图2 不锈钢折弯板二维仿真模型Fig.2 Two-dimensional simulation model of stainless steel bending plate

被测“L”型钢板厚度d= 3 mm，弯角角度为90°，两边板长L1=L2= 300 mm，在折弯与水平方向夹角45°处模拟裂纹缺陷，深度t分别为1 mm(占厚度30%)和0.4 mm(占厚度13%)。在长度为40 mm的激励加载区域(Loading)沿厚度方向施加波结构作为位移载荷，从而激励出指定的频率模态。板两端分别为20 mm 长的完美匹配层(Perfectly matched layer,PML)，用于吸收边界反射波，以获得更好的仿真计算效果。在折弯前后各设置50 mm长的线段A、B，用于探测折弯前后位移的大小。

2.2 仿真结果分析

由于将仿真模型简化为二维，则仅需在激励区域沿x、−y两个方向同时加载波结构的位移分量Ux和Uy进行频域仿真计算。图3 表示0.25 MHz、0.5 MHz和1 MHz的S0模态Lamb波的波结构。通过频域仿真计算得到0.25 MHz、0.5 MHz 和1 MHz的S0 模态仿真计算结果，如图4～图6所示，其中图(a)、(b)和(c)分别为缺陷尺寸为0 mm、0.4 mm和1 mm 时折弯前后的位移波形图。利用A、B两段长度内位移的变化情况，分析不同尺寸缺陷对导波传播的影响作用以及不同频率S0 模态Lamb 波对裂纹缺陷的敏感性。图中实线、虚线分别代表折弯前后的位移图。

图4 0.25 MHz-S0 模态Lamb 波折弯前后位移图Fig.4 Displacement of 0.25 MHz-S0 mode Lamb wave before and after bending

图5 0.5 MHz-S0 模态Lamb 波折弯前后位移图Fig.5 Displacement of 0.5 MHz-S0 mode Lamb wave before and after bending

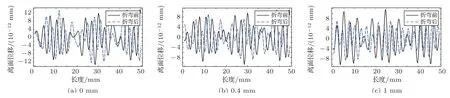
图6 1 MHz-S0 模态Lamb 波折弯前后位移图Fig.6 Displacement of 1 MHz-S0 mode Lamb wave before and after bending

对比3 种频率的S0 模态，当不存在裂纹时，折弯后的B 段位移波形相较折弯前的A 段，其最大值发生了衰减，但衰减并不明显，均未超过5%。当存在裂纹时，B段的位移最大值明显衰减，这表明裂纹对Lamb波具有衰减作用。同时，位移波形的形状发生变化也可表明Lamb 波的模态发生转变。对比图7 中3 种频率的S0 模态检测效果可以看出，裂纹对1 MHz的S0模态的衰减作用最为明显，且随着裂纹尺寸的增大规律变化，可应用于该两种尺寸裂纹的检测和识别。0.5 MHz 也能够实现相应功能，但由于位移变化率小于1 MHz 的S0 模态，故灵敏度较其也有所降低。当频率为0.25 MHz 时，由于两种裂纹的位移变化率仅相差1%，故可用于检出裂纹，但不适用于对其尺寸大小的分辨。

图7 折弯前后Lamb 波位移变化率Fig.7 Displacement change rate of Lamb wave before and after bending

3 不锈钢折弯板裂纹Lamb波检测实验

3.1 实验系统

采用斜入射的激励方式激励所需Lamb 波，入射斜角的大小与楔块的材料和激励的模态有关，根据Snell定律计算可得：

其中，c是楔块的纵波声速，cp是Lamb 波的相速度。激励信号通常为单频正弦信号加窗的单频窄带宽信号。选择5 个周期的正弦信号作为激励信号，Hanning 窗函数作为调制信号如图8所示，可以降低能量在中心频率的耗散，具有更好的检测效果。

图8 激励信号Fig.8 Excitation signal

实验试样为201 不锈钢90°折弯板，如图9所示。在弯角的对称位置使用电火花刻伤机加工出矩形槽模拟裂纹，尺寸(深×宽×长)分别为0.4 mm×0.1 mm×10 mm 和1 mm×0.1 mm×10 mm。采用脉冲回波法进行检测，利用超声收发仪激励超声探头经变角度斜楔在钢板上激发出Lamb 波，并对探头接收到的信号进行前置处理后，在示波器上显示和测量。检测系统示意图如图10(a)所示，实物图如图10(b)所示。3 种频率的群速度、相速度以及对应的斜楔入射角度等参数如表2所示。

表2 实验参数Table 2 Experimental parameters

图9 不锈钢折弯板Fig.9 Stainless steel bending plate

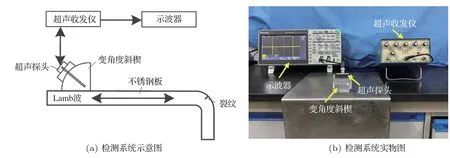
图10 不锈钢折弯板裂纹缺陷检测系统Fig.10 Stainless steel bending plate crack defect detection system

3.2 Lamb波时域信号分析

对缺陷信号类型的分析过程中，最重要的步骤就是提取包含缺陷信息信号的特征量，通常选用回波波包的幅值变化量。图11～图13为Lamb波时域回波信号，图中标注的数字为回波信号幅值。通过计算群速度，对激励出的Lamb波模态进行验证，证明所激励Lamb波与理论值基本相同。

图11 0.25 MHz-S0 模态Lamb 波时域回波信号Fig.11 0.25 MHz-S0 mode Lamb wave time-domain echo signal

图13 1 MHz-S0 模态Lamb 波时域回波信号Fig.13 1 MHz-S0 mode Lamb wave time-domain echo signal

对比无裂纹时的波形，可以看出3 种频率S0 模态均能够检出裂纹缺陷。0.5 MHz和1 MHz 均能够通过判断幅值变化的方法对不同尺寸的裂纹进行识别，但0.25 MHz 对不同尺寸裂纹的区别能力不强，无法用于对裂纹定量的识别。这与仿真得到的结果相吻合。但由于实验中存在外部噪声干扰、设备误差等因素，波形中杂波较多，仅使用时域幅值变化来直观判断裂纹大小不具有较高的可靠性。同时，由于从时域获得的信息是有限的，所以有必要对信号进行频域分析。

WPT 是基于多分辨率分析的思想对非平稳信号进行精细分析。用递归滤波操作将输出信号由高到低地在较宽频带上进行同步连续的分解，根据频段的变化自适应地确定信号分辨率的取值，形成既有低频又有高频的能量组成［14]，可以更加精细地识别信号特征。图14 表示时域信号等效变换为在二叉树中第三层的小波包的分解过程。

图12 0.5 MHz-S0 模态Lamb 波时域回波信号Fig.12 0.5 MHz-S0 mode Lamb wave time-domain echo signal

图14 三层小波包分解结构树Fig.14 Three-layer wavelet packet decomposition structure tree

将一个待识别的能量有限信号f(t)经j层小波包分解，原始信号被分解为2j个子信号，即

定义经分解后的最外层信号中各个频带子信号能量向量为

其中，ei为最外层第i个子信号的能量大小，因此信号总能量E为

定义最外层各频带能量占被分解信号的总能量比值为Pi，则有

本文采用小波包分解对回波信号进行5 层分解，可以将信号频率范围分解成32 个频段，在分解后的频带上进行能量统计，选取频带能量与信号总能量之比Pi作为特征值。通过分析裂纹缺陷对不同频带能量分布的影响，选择与裂纹尺寸相关的敏感频带对裂纹长度进行识别。

图15 为0.25 MHz、0.5 MHz 和1 MHz 的时域检测回波信号经5 层小波变换后，32 个节点的能量占比分布图。可以看出，由于裂纹的存在，导致各频带能量分布发生明显变化，且不同尺寸裂纹的能量比分布差异较大。可见，利用WPT的方法对含有裂纹缺陷特征的检测信号进行处理是可行的，显著优于将幅值变化作为特征参数的方法。因此，通过对0.25 MHz、0.5 MHz和1 MHz的S0模态Lamb波的能量比分布进行分析，优选出与裂纹尺寸成规律性变化的频带，得到表3～表5。

表5 1 MHz 敏感频带小波包能量占比Table 5 1 MHz sensitive frequency band wavelet packet energy

图15 不同频率Lamb 波能量分布图Fig.15 Energy distribution of Lamb waves at different frequencies

表3 0.25 MHz 敏感频带小波包能量占比Table 3 0.25 MHz sensitive frequency band wavelet packet energy

表4 0.5 MHz 敏感频带小波包能量占比Table 4 0.5 MHz sensitive frequency band wavelet packet energy

4 结论

本文通过仿真和实验相结合的方法，研究了Lamb 波对3 mm 厚“L”形不锈钢板折弯处不同尺寸裂纹的检测问题。选用0.25 MHz、0.5 MHz 和1 MHz 三种频率，采用频域有限元法计算不同频率的S0 模态Lamb 波对深度为0.4 mm、1 mm 裂纹的检测效果，开展了不锈钢折弯板裂纹缺陷的检测实验研究。并采用WPT的方法对实验信号进行分析，得到每种频率Lamb 波的能量分布情况，选取各自敏感频带作为特征量，对不同尺寸裂纹进行检测和识别，具有实际工程应用价值。结果表明：

(1)不锈钢弯板折弯处裂纹缺陷Lamb 波检测的实验结果与仿真结果基本一致，验证了Lamb 波对折弯裂纹缺陷的检测有效性，以及频域有限元仿真模型的正确性。

(2)实验获取的0.5 MHz、1 MHz 的S0 模态时域信号能够检测出深度为0.4 mm 和1 mm 的裂纹缺陷，且能够通过波包幅值变化情况对裂纹尺寸进行识别。

(3)采用WPT 的方法对时域回波信号进行分析，选出频带11为0.25 MHz、0.5 MHz和1 MHz 的S0 模态Lamb 波的敏感频带，能够实现对裂纹缺陷的定量识别，取得更好的检测效果。将检测频率使用范围向低频段延伸，避免了Lamb 波的多模态性。同时，低频Lamb 波衰减小，有效地提高了其使用能力。

由表3～表5 可以得到，0.25 MHz 检测信号的敏感频带为5、11、13；0.5 MHz 的敏感频带为4、11、30；1 MHz 的敏感频带为11、16。可见，不同频率的S0模态Lamb波检测信号的敏感频带不同。所选取的敏感频带能量占比均随裂纹尺寸的增大而增大，利用该规律能够对不同尺寸的裂纹缺陷进行识别。且频带11 对0.4 mm 和1 mm 尺寸的裂纹均敏感，随着裂纹尺寸的增大，频带11 的能量占比增大。故可通过判断频带11 的能量占比变化对裂纹进行检测并对尺寸的大小进行识别。