基于优化反馈的组合在线学习

孔芳，杨悦然，陈卫，李帅

1. 上海交通大学约翰·霍普克罗夫特计算机科学中心，上海 200240；2. 微软亚洲研究院，北京 100080

1 引言

随着数据时代的来临，传统离线学习方法已难以快速处理模型训练所需的爆发式增长的数据量及特征数量，这促进了在线学习模式的发展。在线学习方法接收实时数据流，定义累积懊悔（cumulative regret）取代损失函数作为新的优化函数，利用实时反馈不断迭代调整算法，从而减少离线训练所需的数据量，并提高处理效率。在许多实际问题中，最优解往往不是简单的单个目标，而是多个目标的组合形式，这推进了对组合在线学习问题的研究。组合在线学习问题，即组合多臂老虎机（combinatorial multi-armed bandits，CMAB）问题，结合了在线学习与组合优化，研究如何在与环境交互的过程中自主学习未知参数，逐步找到最优的目标组合，其应用包括社交网络中的广告投放、搜索、推荐等问题。

2 组合在线学习问题

2.1 多臂老虎机问题

多臂老虎机（multi-armed bandits）问题是一个经典的机器学习问题，该问题最初由赌场的老虎机情景演变而来，被建模为玩家与环境之间的T轮在线游戏。老虎机共有m个臂（arm），m个臂的集合即玩家 的 动 作 集 合，记 为每个臂i∈[m]都有各自未知的奖励分布，该分布的期望记作μi。玩家在每一轮游戏t∈[T]拉动其中一个臂，环境将从该臂的奖励分布中采样一个随机变 量XAt,t，作为玩家拉动该臂的奖励值。该奖励值将帮助玩家更新对臂的奖励分布的了解，进而更新其后续选择臂的策略。玩家的目标是最大化T轮的累积期望收益，即最小化与最优臂之间的累积期望收益的距离。令表示最高期望收益，则玩家的目标为最小化累积期望懊悔：

其中，期望取自奖励值产生的随机性及玩家策略的随机性。

有时，玩家在每一轮收到的反馈不仅仅是其本轮拉动臂的奖励（即强盗反馈（bandit feedback）），还可能观察到所有臂的输出，该反馈类型被称为全反馈（full feedback）。玩家收到的反馈信息可用一个反馈图（feedback graph）来表示，图中每个节点表示一个臂，每条有向边(i,j)表示当玩家拉动臂i时可观察到臂j的输出。全反馈类型的反馈图可由完全图表示，即每个节点有指向所有节点（包含自身）的边；强盗反馈类型可用自环图表示，即每个节点仅有指向自身的边。反馈图可进一步泛化，用于表示更复杂的反馈关系[1-2]。除有向图外，矩阵也可用于描述反馈关系。部分监控（partial monitoring）[3]问题就使用反馈矩阵H来描述玩家可获得的反馈信息，并使用损失矩阵L来刻画玩家在游戏中的损失。若玩家在某一轮选择臂i，环境本轮选择臂i的输出为j，则玩家将付出损失Li,j，并观察到反馈Hi,j，通过设计不同的反馈矩阵，Hi,j可给出关于真实输出j的部分或全部有效信息。

通过与环境的多轮交互，玩家将收集到对各个臂的奖励分布的观察。在接下来的游戏中，玩家一方面希望选取历史观察中表现最好的臂，以获取相对较高的收益（开发（exploit））；另一方面希望尝试一些尚未受到足够观察的臂，以获取潜在较高的收益（探索（explore））。过度开发可能导致玩家错过最优臂，过度探索则将导致玩家付出过多的学习代价，如何平衡开发与探索是多臂老虎机算法需要考虑的核心问题。

置信区间上界（upper confidence bound，UCB）[4]和汤姆森采样（Thompson sampling，TS）[5]类型的算法是解决此类多臂老虎机问题的经典方法。UCB类型的算法为每个臂i维持一个置信上界，该上界为过往观察的经验均值与置信半径之和，置信半径将随着被观察到的次数的增多而减小。当一个臂被观察到的次数足够小时，置信半径很大，促使置信上界足够大，算法将倾向于选择这些臂，这体现了探索的思想。当臂被观察到足够多的次数时，置信半径变小，置信上界的值趋近于经验均值，进而趋近于真实的期望值，算法将倾向于选择经验均值高的臂，这体现了开发的思想。TS类型的算法则为每个臂维持一个关于其奖励值的先验分布，初始时算法对臂的收益尚未了解，该分布趋近于一个均匀分布，体现了探索的思想；随着收集到的观察的增多，该分布逐渐集中于经验均值附近，方差变小，这体现了开发的思想。

上述策略均以最大化累积期望奖励/最小化累积期望懊悔为目标，然而考虑这样的应用场景，在疫情期间，医学研究人员有多种药物的配置方式及一些可供测试药物效果的小鼠，研究人员希望在小鼠身上实验后为人类找到最有效的药物配置方式，该目标与小鼠本身的奖励无关。这种问题被称为纯探索（pure exploration）问题，玩家有一定的预算轮数，在这段时间内可以拉动不同的臂，并观察其输出，预算轮数终止后，需要给出最终的推荐，即拉动不同臂的概率分布。简单懊悔（simple regret）是用来衡量解决此类问题策略的标准，其被定义为最优臂的期望奖励与最终推荐的期望奖励之差[6]。当玩家的最终目标是经过探索后识别出最优的臂时，该问题被称为最佳手臂识别（best arm identification）问题，是纯探索问题的一种变体[7]。该问题也有两种目标，当探索预算固定时，玩家需要最大化识别出最优臂的概率[8]；当返回最优臂的概率固定时，玩家的目标为最小化探索所需付出的代价[9]。

此外，在有些应用场景中，玩家有额外的探索限制，如商家希望在每一轮广告投放时，都能保证一定值的收益，即保守型探索（conservative exploration），服从保守型探索限制的问题被称为保守型老虎机（conservative bandits）问题[10]。给定一个基准臂A0，保守型探索限制玩家每一轮游戏t选 择 的 臂At满 足，其中α用于衡量玩家的保守程度，α越小，意味着玩家越保守。

在上述场景中，每个臂的奖励值服从一个固定的概率分布，此时称反馈类型为静态反馈（stationary feedback）；当每个臂奖励值服从的概率分布随时间发生变化时，称反馈类型为非静态反馈（nonstationary feedback）；当每一轮的信息不在这一轮实时反馈给玩家，而是会有一定延迟的时候，称此反馈为延迟反馈（delayed feedback）。此外，多臂老虎机问题还有许多丰富的变种。当每个臂的奖励值不再服从一个确定的概率分布，而是一系列的确定值时，该问题将变为对抗老虎机（adversarial bandit）问题，Exp3算法[11]是解决此类多臂老虎机问题的经典算法。若每个臂的期望收益与玩家所获得的环境特征相关，则称为情境式老虎机（contextual bandit）问题。在情境式老虎机问题中，若臂的期望收益是情境信息向量的线性加权形式，则称为线性老虎机（linear bandit）问题，LinUCB算法[12]是解决此问题的经典算法；若每一轮玩家拉动的不再是单独的臂，而是多个臂的组合，则该问题变为组合多臂老虎机问题，即组合在线学习问题。

2.2 组合多臂老虎机问题

在许多应用场景中，玩家拉动的不是单独的一个臂，而是多个臂的组合。如出行推荐平台需要向用户推荐的通常是机票、酒店与景区门票的组合，这时便需要组合多臂老虎机的研究框架来解决。

Gai Y等人[13]最早将多用户信道分配问题建模为一个组合多臂老虎机模型，在该模型中，每个臂包含多个组件的组合，拉动同一个臂的奖励随时间相互独立，但是不同臂之间的奖励会由于一些共享的部件而产生依赖关系。之后，该框架又被进一步泛化，并被系统地阐释[14-17]。

组合在线学习同样被建模为玩家与环境之间的T轮在线游戏。该问题包含m个基础臂（base arm），所有基础臂组成的集合被记为。每 个 基 础臂维持其各自的奖励分布，奖励的期望记为μi。第t轮基础臂i的输出记为Xi,t，为环境从该臂的奖励分布中采样出的随机变量，且是相互独立的。记所有基础臂的奖励期望为，所有基础 臂在第t轮 的 输出为玩家可选择的动作是所有m个基础臂可能的组合，称之为超级臂（super arm），记S为动作集合，则。在每一轮中，玩家拉动超级臂，随后获取本轮的奖励，并观察环境的反馈信息。玩家收到的奖励值将与拉动超级臂中包含的所有基础臂的输出相关。若该值为每个基础臂的输出（加权）之和，则称奖励为线性形式[17]。但在实际应用场景中，拉动超级臂的奖励形式可能更加复杂，如在推荐场景中用户的点击情况可能不直接线性依赖于平台推荐的每一个项目的吸引力，此时奖励被称为非线性形式[14-16]。玩家收集到的反馈信息也将根据不同的应用场景有所不同，可分为以下3类。

● 全信息反馈：该反馈类型假设玩家在拉动一个超级臂之后，能够观察到所有基础臂的输出，而与该基础臂是否被包含在被拉动的超级臂中无关。这是一种非常理想化的设定，现实中往往难以遇到该场景。

● 半强盗反馈：全信息反馈的设定较为理想，现实中更常见的模式是玩家只能观察到其选择的超级臂包含的基础臂的反馈信息，也就是半强盗反馈。例如，在搜索排序场景中，平台可以获取用户对所列举项目的满意程度。

● 强盗反馈：该反馈类型假设玩家只能观察到拉动超级臂所获得的总的奖励，而不能看到任何基础臂的信息。以推荐场景为例，用户的点击意味着对所推荐商品组合的认可，平台往往无法获知用户对具体某个产品的满意程度。

类似多臂老虎机问题，组合多臂老虎机的反馈类型也可分为静态反馈、非静态反馈、延迟反馈等。根据每一轮收集到的反馈信息，玩家将进一步更新自己的策略。

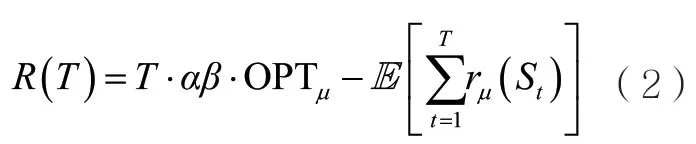
受到一些应用场景的启发，玩家在拉动一个超级臂St∈S后，除St中包含的基础臂外，更多的基础臂可能会被St随机触发，对玩家最终的收益产生影响。该问题被建模为带概率触发臂的组合多臂老虎机（CMAB with probabilistically triggered arms，CMAB-T）模型[15,18]，得到了较多的关注。

注意到在情境式线性老虎机模型中，学习者在每一轮拉动一个由向量表示的动作，并收到与该动作向量线性相关的奖励值，线性函数的参数即学习者需要学习的未知参数向量。故线性多臂老虎机模型也可被视为基于线性奖励形式、强盗反馈类型的组合多臂老虎机问题。研究者通常通过采用为未知参数向量构造置信椭球（confidence ellipsoid）的方法来解决此类问题[19-21]。

此外，多臂老虎机问题还可与组合数学中的拟阵结构相结合，即拟阵老虎机（matriod bandit）模型。该模型最早由Kveton B等人[22]提出，拟阵可由二元组表示，其中是由m个物品组成的集合，称为基础集（ground set）；I是由E的子集组成的集合，称为独立集（independent set），且需要满足以下3点性质：①∅∈I；②I中每个元素的子集是独立的；③增加属性（augmentation property）。加权拟阵老虎机假设拟阵会关联一个权重向量，其中w(e)表示元素e∈E的权重，玩家每次拉动的动作A∈I的收益为。该问题假设拟阵是已知的，权重w(e)将随机从某未知的分布P中采样得到。对应到组合多臂老虎机模型，E中的每个物品可被看作一个基础臂，I中的每个元素可被看作一个超级臂。玩家的目标是寻找最优的超级臂，最小化T轮游戏拉动超级臂所获期望收益与最优期望收益之间的差，即累积期望懊悔值。

纯探索问题在组合场景下也得到了进一步的研究。Chen S等人[23]首先提出了多臂老虎机的组合纯探索（combinatorial pure exploration of multi-armed bandits）问题。在该问题中，玩家在每一轮选择一个基础臂，并观察到随机奖励，在探索阶段结束后，推荐出其认为拥有最高期望奖励的超级臂，其中超级臂的期望奖励为其包含基础臂的期望奖励之和。Gabillon V等人[24]在相同的模型下研究了具有更低学习复杂度的算法。由于允许玩家直接观察到其选择的基础臂的输出这一假设在实际应用场景中过于理想化，上述模型随后被进一步泛化。Kuroki Y等人[25]研究了玩家在每一轮选择一个超级臂并仅能观察到该超级臂包含基础臂随机奖励之和的情况，即全强盗线性反馈的组合纯探索（combinatorial pure exploration with full-bandit linear feedback）问题，并提出了非自适应性的算法来解决此问题。之后，Rejwan I等人[26]提出了自适应性的组合相继接受与拒绝（combinatorial successive accepts and rejects，CSAR）算法来解决此类问题中返回前K个最优基础臂的情况。Huang W R等人[27]泛化了线性奖励形式，研究了具有连续和可分离奖励函数的场景，并设计了自适应的一致最佳置信区间（consistently optimal confidence interval，COCI）算法。Chen W等人[28]提出了一种新的泛化模型——带有部分线性反馈的组合纯探索（combinatorial pure exploration with partial linear feedback，CPE-PL）问题，涵盖了上述全强盗线性反馈以及半强盗反馈、部分反馈、非线性奖励形式等场景，并给出了解决此模型的首个多项式时间复杂度的算法。在实际应用场景中，玩家可能无法观察到某个臂的准确反馈，而是多个臂之间的相对信息，即竞争老虎机（dueling bandit）模型。Chen W等人[29]研究了竞争老虎机的组合纯探索（combinatorial pure exploration for dueling bandits）问题，并设计了算法解决不同最优解定义的问题场景。

当每个基础臂的收益值不再服从特定的概率分布，而是一系列的确定值时，上述问题将变成对抗组合多臂老虎机（adversarial CMAB）问题，相关研究工作将在下一节中基于强盗反馈的CMAB算法部分一并介绍。

3 基于优化反馈的组合在线学习算法

Gai Y 等人[17]最早考虑了组合多臂老虎机中奖励形式为线性的情况，提出了线性奖励学习（learning with linear reward，LLR）算法解决此问题，具体如下。

算法1：LLR算法

初始化：L为每个超级臂包含基础臂的个数，t=0

Fori=1 tom

t=t+1

选择有基础臂i的超级臂

更新基础臂i的奖励估计以及基础臂i被选择的次数Ti,t

End for

While True do

t=t+1

对于 ∀i∈Aa，更新基础臂i的收益估计以及基础臂i被选择次数Ti,t

End while

L LR算法使用UCB的思想平衡开发与探索的关系。在该算法中，学习者每轮可选择的超级臂中至多包含L个基础臂，其中L为超参数。每个超级臂Aa被表示为所有基础臂的加权组合，权重向量由m维的向量a表示，ai≥ 0表示基础臂i在超级臂中的权重，Aa将包含所有满足ai≠ 0的基础臂i。超级臂的置信上界是其包含的基础臂的置信上界的加权和，算法在每一轮选择置信上界最大的超级臂。该算法框架有丰富的应用场景，如寻找最大匹配、计算最短路径及最小生成树等。

随后，Chen W等人[14-16]泛化了奖励的形式，考虑到非线性形式的奖励，且受到一些实际应用场景（如影响力最大化等）的启发，提出了带概率触发机制的组合多臂老虎机（CMAB with probabilistically triggered arms，CMAB-T）模型，并设计组合置信区间上界（combinatorial upper confidence bound，CUCB）算法来解决此类问题，具体如下。

算法2：CUCB算法

输入：基础臂集合[m]，离线神谕Oracle

While True do

执行动作S，观察到所有被触发的基础臂i，更新Ti和

End while

与LLR算法类似，CUCB算法同样在每一轮为所有基础臂计算其置信上界，不同之处在于选择超级臂的方法不同。CUCB算法考虑了更多的应用场景，定义了一个更广泛的求解超级臂的方法。算法获取一个离线神谕作为输入，将根据输入的每个基础臂的置信上界，输出该参数下最优（或近似最优）的超级臂，算法进而执行此超级臂，并观察相应的信息。由于许多非线性奖励形式的离线组合优化问题通常为NP难问题，该算法允许借助近似的离线神谕来帮助每一轮中超级臂的选取，且使用近似累积懊悔上界指标来衡量算法的性能。

通过为具体的CMAB-T问题实例寻找合适的受触发概率调制的有界平滑性条件（triggering probability modulated condition，TPM条件），CUCB算法可以达到的累积懊悔上界[15]，其中B为TPM条件的参数，K为所有超级臂中可随机触发的基础臂的最大个数。TPM条件的具体内容见条件1。

条件1（TPM条件）：若存在有界平滑常数，使得对于任意两个基础臂分布（期望分别记为µ和µ′），任意超级臂S，满足，则称该CMAB-T问题实例满足1范数TPM条件。其中，为超级臂S成功触发基础臂i的概率。

概括来说，TPM条件通过所有基础臂在不同环境中的期望奖励之差的加权和约束了同一个超级臂在对应奖励分布下的奖励差异，每个基础臂的权重就是其在该超臂下被成功触发进而对超级臂奖励产生影响的概率。寻找合适的TPM条件对于该类问题的理论分析有重要的作用，如在线影响力最大化、基于特定点击模型的搜索排序问题等。

之后，Combes R等人[30]尝试了与LLR和CUCB不同的计算置信上界的方法，自然推广KL-UCB[31]中的指标（index），利用KL散度来确定置信区间，并提出了ESCB（efficient sampling for combinatorial bandits）算法解决线性奖励形式的CMAB问题。但由于超级臂数量随着基础臂数量的增加呈指数增长，该算法每一轮需要付出指数时间计算所有超级臂的置信上界。最近，Cuvelier T等人[32]提出了一个近似ESCB算法，算法能达到和ESCB一样的累积懊悔上界，但实现了多项式时间复杂度O(Tpoly(m))。

此外，上述CMAB问题还可拓展至与情境相关的情况，即每轮玩家都会收到当前的情境信息，每个基础臂的期望奖励值会与该情境信息相关，该问题被称为情境式CMAB（contextual CMAB）问题，由Qin L J等人[33]最早提出。在该工作中，每个基础臂i的期望奖励值都会与此轮的情境信息线性相关，其中xt(i)是描述情境信息的向量， 是噪声项，而超级臂的奖励值与超级臂中包含的基础臂的奖励值有关，可以是简单的加权和，也可以是非线性关系。参考文献[33]针对这样的问题框架提出了C2UCB算法，在UCB算法的基础上，加入了对参数θ的拟合过程，达到了阶的累积懊悔上界，其中d是情境信息向量的维数。Chen L X等人[34]推广了上述框架，考虑了玩家可选的基础臂集合会随时间发生变化的情况，并提出了CC-MAB算法来解决此类问题。随后Zuo J H等人[35]提出了另一种广义情境式CMAB-T（context CMAB-T）的框架——C2MAB-T。该框架考虑了给定情境信息之后，玩家可选的动作会受到该情境信息的限制。具体来说，在每一轮环境会先提供一个可选超级臂集，而玩家这一轮可选择的超级臂就被限制在该集合中，其选择的超级臂会随机触发更多的基础臂，玩家最终观察到所有触发臂的反馈。参考文献[35]提出了C2-UCB、C2-OFU算法来解决此类问题，并证明了在近似离线神谕下，累积懊悔上界均为，其中m是基础臂的数量，K是所有超级臂可触发基础臂的最大数量。

总体来说，上述研究工作均基于UCB类型的算法处理开发与平衡的关系。除此之外，也有一系列基于TS的方法解决CMAB问题。

Komiyama J等人[36]研究用TS算法解决组合多臂老虎机中超级臂的奖励为所包含基础臂的输出之和且超级臂的大小固定为K的问题，提出了多动作汤姆森采样（multiple-play Thompson sampling，MP-TS）算法。该工作考虑了基础臂的输出为伯努利随机变量的场景，算法为每个基础 臂维 持 一 个贝塔 分布在每一轮将为每个基础臂i从其分布中采样一个随机变量θi，并对所有基础臂根据该随机变量从高到低排序，从中选择前K个基础臂组成本轮要选择的超级臂，随后根据这些基础臂的输出再次更新其对应的贝塔分布。MP-TS算法达到了的累积懊悔上界，其中为任意非最优基础臂i与最优臂K期望奖励的KL距离，该懊悔值上界也与此类问题的最优懊悔值相匹配。

之后，Wang S W等人[37]研究如何用TS算法解决广义奖励形式的组合多臂老虎机问题，提出了组合汤姆森采样（combinatorial Thompson sampling, CTS）算法，具体见算法3。

算法3：CTS算法

While True do

t←t+1

对于每个基础臂i，从贝塔分布随机 采样

计算S=Oracle(θ(t))

执行动作S，得到观察

End while

与CUCB算法相同，CTS算法同样借助离线神谕产生给定参数下的最优超级臂，但该算法要求能够产生最优解，不像CUCB算法那样允许使用近似解。与MP-TS相比，CTS算法将基础臂的输出由伯努利类型的随机变量放宽到[0,1]区间，且允许超级臂的奖励是关于基础臂输出更为广泛的形式，而不再是简单的线性相加。当超级臂的期望奖励值与基础臂的奖励期望满足利普希茨连续性条件（Lipschitz continuity）时，该工作给出了基于TS策略解决广泛奖励形式的CMAB问题的首个与具体问题相关的累积懊悔上 界，其 中K为所 有 超 级臂中包含基础臂的最大个数，∆min为最优解和次优解之间的最小差。该懊悔值上界也与基于同样条件获得的UCB类型的策略（CUCB算法）的理论分析相匹配[14]。当奖励形式满足线性关系时，该算法的累积懊悔上界可被提升至[38]。

此外，Hüyük A等人[39-40]同样基于确定的离线神谕Oracle，考虑到带概率触发的基础臂，研究用CTS策略解决CMAB-T问题。当超级臂的期望奖励与基础臂的奖励期望满足利普希茨连续性条件时，该工作证明CTS算法在该问题场景下可以达到的累积懊悔上界，其中pi为基础臂i被所有超级臂随机触发的最小概率。该结果也与基于同样条件的UCB类型的策略（CUCB算法）的理论分析相匹配[14]。

具体到拟阵老虎机问题，Kveton B等人[22]充分挖掘拟阵结构，提出了乐观拟阵最大化（optimistic matriod maximization，OMM）算法来解决此问题。该算法利用UCB的思想，每轮选取最大置信上界的超级臂，并且通过反馈进行参数更新，优化目标是令累积懊悔最小化。该文献分别给出了OMM算法与具体问题相关的遗憾值上界和与具体问题无关的累积懊悔上界，其中K为最优超级臂A*的大小，是非最优基础臂e和第Ke个最优基础臂的权重期望之差，Ke为满足大于0的元素个数。通过分析，拟阵多臂老虎机问题可达到的累积懊悔值下界为，该结果也与OMM算法可达到的累积懊悔上界相匹配。Chen W等人[41]也给出了利用CTS算法解决拟阵多臂老虎机问题的理论分析，该算法的累积懊悔上界也可匹配拟阵多臂老虎机问题的累积懊悔下界。

当每个臂的奖励值服从的概率分布随时间发生变化时，问题将变为非静态组合多臂老虎机。Zhou H Z等人[42]最早研究了非静态反馈的CMAB问题，并在问题设定中添加了限制——基础臂的奖励分布变化总次数S是。文中提出了基于广义似然比检验的CUCB（CUCB with generalized likelihood ratio test，GLR-CUCB）算法，在合适的参数下，若总基础臂数量m已知，则累积懊悔上界为；若m未知，则累积懊悔上界为，其中 C1、 C2为与具 体问 题相关的常数。而后Chen W等人[43]推广了设定，即忽略上述对S大小的假设，引入变量衡量概率分布变化的方差，在S或者V中存在一个已知时，提出了基于滑动窗口的CUCB（sliding window CUCB，CUCBSW）算法，其累积懊悔上界为或者；在S和V都未知时，提出了基于两层嵌套老虎机的CUCB（CUCB with bandit-over-bandit，CUCB-BoB）算法，在特定情况下，该算法累积懊悔上界为T的次线性数量级。

此外，CMAB问题也可以拓展至保守探索模式。Zhang X J 等人[44]最早将Wu Y F等人[10]提出的保守型多臂老虎机问题衍生到CMAB问题框架中，即第t轮用户选择的超级臂的奖励值µt和默认超级臂的奖励值µ0的关系服从限制，其中α用于 衡 量 用户的保守程度，α越小意味着用户越保守。该文献基于UCB的思想提出了情境式组合保守UCB（contextual combinatorial conservative UCB，CCConUCB）算法，同时针对保守选择的默认超臂的奖励值0µ是否已知，分别提出了具体算法。当保守选择的奖励值已知时，算法的累积懊悔为，其 中d为基础臂的特征维数，K为超级臂中最多能包含的基础臂的数量。

上述CMAB研究工作均基于半强盗反馈，即超级臂中包含的（及触发的）所有基础臂的输出都可以被玩家观察到，也有部分工作研究了基于强盗反馈的CMAB算法。这类算法多考虑对抗组合多臂老虎机问题（adversarial CMAB），即每个基础臂的输出不再服从一个概率分布，而是一系列的确定值。Cersa-Bianchi N 等人[45]首先提出了COMBAND算法来解决此问题，该工作使用来体现组合关系，其中表示由基 础臂组成的超级臂，当P的最小特征值满足一定条件时，算法可达到的累积懊悔上界。Bubeck S等人[46]提出了基于约翰探索的EXP2（EXP2 with John’s exploration）算法，该算法也可达到的累积懊悔上界。Combes R等人[30]考虑通过将KL散度投影到概率空间计算基础臂权重的近似概率分布的方法来减少计算复杂度，提出了更有效的COMBEXP算法，该算法对于多数问题也可达到相同的累积懊悔上界。Sakaue S等人[47]进一步考虑了更加复杂的超级臂集合的情况，设计了引入权重修改的COMBAND（COMBAND with weight modification，COMBWM）算法，该算法对于解决基于网络结构的对抗组合多臂老虎机问题尤其有效。

当玩家需要拉动的动作为多个臂的组合时，其获得的反馈也会随实际应用场景变得更加复杂，部分监控问题在此场景下得到了进一步的研究，即组合部分监控（combinatorial partial monintoring）。Lin T等人[48]最早结合组合多臂老虎机与部分监控问题，提出了组合部分监控模型，以同时解决有限反馈信息、指数大的动作空间以及无限大的输出空间的问题，并提出了全局置信上界（global confidence bound，GCB）算法来解决线性奖励的场景，分别达到了与具体问题独立的和与具体问题相关的的累积懊悔上界。GCB算法依赖于两个分别的离线神谕，且其与具体问题相关的的累积懊悔 上界需要 保证问题最优解的唯一性，Chaudhuri S等人[49]放宽了这些限制，提出了基于贪心开发的阶段性探索（phased exploration with greedy exploitation，PEGE）算法来解决同样的问题，达到了与具体问题独立的和与具体问题相关的的累积懊悔上界。

在一些应用场景中，如推荐系统等，随着时间推移，系统将收集到越来越多的用户私人信息，这引起了人们对数据隐私的关注，故CMAB算法还可以与差分隐私（differential privacy）相结合，用于消除实际应用对数据隐私的依赖性。Chen X Y等人[50]研究了在差分隐私和局部差分隐私（local differential privacy）场景下带半强盗反馈的组合多臂老虎机问题，该工作证明了当具体CMAB问题的奖励函数满足某种有界平滑条件时，算法可以保护差分隐私，并给出了在两种场景下的新算法及其累积懊悔上界。

4 应用方面

组合多臂老虎机问题框架有非常丰富的实际应用，本文着重介绍在线排序学习和在线影响力最大化两类问题。

4.1 在线排序学习问题

排序学习问题主要研究如何根据目标的特征对目标进行排序，是机器学习算法在信息检索领域的一个应用。该问题有一个目标物品集L，学习者每次需要根据某种打分标准对整个目标集进行打分，并且将打分进行排序，推荐出前K（通常L≫K）个分数最高的目标物品。该问题有丰富的应用场景，如搜索、推荐、广告点击等。

在许多真实的应用场景中，如广告推荐、搜索引擎排序等，总商品集的数量远远大于需要推荐的商品数量，使得离线排序学习模型所需训练数据巨大，学习任务更加艰巨，这推动了对在线排序学习（online learning to rank）的研究。在线排序学习问题不再需要大量的历史数据来构建排序模型，学习者将在与用户的T轮交互过程中不断更新对目标物品的评估。由于学习者需要推荐多个目标的组合，该问题属于组合多臂老虎机的研究范畴，每个目标物品对应一个基础臂，而推荐的物品组合对应一个超级臂。

在线排序学习算法早期多由经典的多臂老虎机问题算法改进而来，例如Li L H等人[12]改进了LinUCB（linear UCB）算法，考虑了项目的特征的加权组合，并通过计算置信上界来解决排序问题，Chen Y W等人[51]改进了LinUCB算法，在探索时引入贪心算法，优化了在线排序学习算法。

近年来，在线排序学习的研究工作多基于点击模型。以商品推荐问题为例，商家考虑如何向用户推荐商品，在与用户的T轮交互过程中，学习商品的特征与用户的喜好之间的关系，使用户在轮推荐中尽可能多地点击其推荐的商品。商家每次向用户推荐的商品数量有限，推荐形式通常为列表。在每一轮推荐之后，商家可获取用户的点击反馈，通常来说，若用户点击了其推荐的某个商品，则反馈为1，否则反馈为0。

上述点击模型可分为3个部分：用户是否浏览某个商品、商品对用户的吸引程度以及用户最终的点击情况。用户的浏览行为和商品对用户的吸引力共同决定了用户最终是否点击。根据用户的点击行为，点击模型可进一步分为级联模型（cascade model）、依赖点击模型（dependent click model）、基于位置的模型（position-based model）等。

级联模型假设用户至多点击一次被推荐的商品列表（大小为K），即用户会从列表的第一个商品开始，依次向后浏览，一旦点击某个商品，用户将停止继续浏览。Kveton B等人[52]首先提出了析取目标（disjunctive objective）形式的级联模型，即被推荐的商品列表中只要有一个“好”的商品，奖励值为1，且考虑了所有可推荐的商品列表形成均匀拟阵的情况，并提出了CascadeKL-UCB算法解决该问题。该算法达到了的累积懊悔上界，其中Δ表示最优点击期望和次优点击期望之间的差的最小值。而后Kveton B等人[53]推广了问题框架，提出了组合级联模型，在该框架下推荐的商品列表只需满足某些组合限制即可。该工作研究了合取目标（conjunctive objective），即只有所有商品都是“好”商品时，奖励值才为1。作者提出了CombCascade算法解决此问题，达 到了的累积懊悔上界，f*是最优超级臂的收益。Li S等人[54]进一步考虑了商品的情境信息（contextual information），并提出了C3-UCB算法，算法的累积懊悔上界为，d为刻画情境信息的特征维数。

依赖点击模型放宽了级联模型对用户点击次数的限制，允许用户在每次点击之后仍以λ的概率选择继续浏览，即最终的点击数量可以大于1。在λ=1时，Katariya S等人[55]基于此模型结合KL-UCB算法[31]设计了dcmKL-UCB算法，取得了的累积懊悔上界。Cao J Y等人[56]推广了问题设定，考虑了λ不一定为1的情况，并且考虑了用户疲劳的情况（即用户浏览越多，商品对用户的吸引能力越弱），在疲劳折损因子已知的情况下提出了FA-DCM-P算法，算法的累积懊悔上界是；若疲劳折损因子未知，作者提出了FA-DCM算法，算法累积懊悔上界为

相较于前两个点击模型，基于位置的模型考虑了用户对不同位置商品的浏览概率的变化，即用户对商品的浏览概率将随着该商品在推荐列表中顺序的后移而逐渐变小。Li C等人[57]基于冒泡排序算法的思想设计了BubbleRank算法，该算法可同时适用于级联模型和基于位置的模型。Zoghi M等人[58]引入了KL标度引理，设计了BatchRank算法。该算法也可同时应用于级联模型和基于位置的模型。

Zhu Z A等人[59]不再考虑某特定的模型假设，而是根据实际推荐点击场景提出了更通用的广义点击模型，上述3种模型均可涵盖在内。广义点击模型假设用户浏览每个商品的概率随着商品在推荐列表中位置的后移而减小。用户点击某商品的概率与该商品的吸引力相关，且用户继续往后浏览的概率与其对当前商品的点击与否相关。用户对商品列表整体的浏览及点击情况可由如图1所示的贝叶斯网络结构来阐释。图1中Ai表示用户点击第i个商品后继续向下浏览，Bi表示用户没有点击第i个商品并继续向下浏览，Ei表示用户浏览第i个商品，Ci表示用户点击第i个商品，Ri表示第i个商品的相关程度/吸引力，即用户的浏览行为与商品的吸引力共同决定了用户对该商品的点击行为，而用户浏览第i+1个商品的可能性与用户对第i个商品采取行为的概率分布相关。

图1 广义点击模型的贝叶斯网络结构

针对上述广义模型，Li S等人[60]考虑到广义模型中每次反馈可能有噪声影响，且假设点击概率和浏览每个商品的概率独立，同时与每个商品的吸引力也独立，提出了RecurRank算法。该算法利用递归的思想，考虑将排序分为若干阶段，每个阶段都采用分段排序，下一个阶段再对已经分得的段继续分段排序，直至最后排序完成，算法的懊悔上界为，其中d为商品的特征维数；Lattimore T等人[61]基于BatchRank的结果提出了TopRank算法，该算法学习商品之间吸引力大小的相对关系，从而完成排序任务。相比于BatchRank，该算法应用更加广泛，计算更加简便且懊悔上界更小。

此外，线性次模多臂老虎机（linear submodular MAB）模型是应用于在线排序学习领域的另一经典 老虎机模型。该模型最早由Yue Y S等人[62]提出，将次模信息覆盖模型引入组合多臂老虎机框架，并应用于排序学习领域。次模信息覆盖模型假设信息的边际效益递减。该模型假设任意商品a都可被d个基本 覆盖函数F1,…,Fd表示，其中基本 覆 盖函数F1,… ,Fd表 示此文档对d个特征的覆盖率，且为已知的满足次模性质的函数。同理，每个商品对应组合多臂老虎机模型的基础臂，需要推荐的有序商品组合为超级臂，超级臂的覆盖函数是基础臂覆盖函数的加权和。Yue Y S等人[62]提出了LSBGreedy算法来解决此问题，并证明其累积懊悔上界为其中L是超级臂中包含的基础臂的数量，S是与权衡期望收益和噪声的参数相关的常数。然而问题原始定义是将所有商品都进行排序输出，即最终得到的超级臂是，这并不符合多数排序学习问题的实际情况，此后Yu B S 等人[63]引入了背包限制（即每个文档有成本函数，需要考虑推荐的文档的成本总和不能超过某个限制值），并提出了两种贪心算法（MCSGreedy和CGreedy）来求解此类问题。Chen L等人[64]把原始线性次模问题推广到无限维，考虑了边际收益函数是属于再生核希尔伯特空间的具有有限模的元素，并提出了SM-UCB算法。Takemori S等人[65]考虑了双重限制下的次模多臂老虎机问题，即背包限制以及k-系统限制，沿用改进UCB的思想，提出了AFSM-UCB算法，相比于LSBGreedy[62]和CGreedy[63]，该算法在实际应用效率方面有一定程度的提升。

4.2 在线影响力最大化

在线影响力最大化（online influence maximization，OIM）问题研究在社交网络中影响概率未知的情况下，如何选取一组种子节点集合（用户集合），使得其最终影响的用户数量最大[66]。该问题有丰富的应用场景，如病毒营销、推荐系统等。由于学习者选择的动作是多个节点的组合，动作的数量会随着网络中节点个数的增长出现组合爆炸的问题，故在线影响力最大化也属于组合在线学习的研究范畴。

独立级联（independent cascade，IC）模型与线性阈值（linear threshold，LT）模型是描述信息在社交网络中传播的两个主流模型[67]。在IC模型中，信息在每条边上的传播被假设为相互独立，当某一时刻节点被成功激活时，它会尝试激活所有的出邻居v一次，激活成功的概率即边的权重，该激活尝试与其他所有的激活尝试都是相互独立的。LT模型抛弃了IC模型所有传播相互独立的假设，考虑了社交网络中常见的从众行为。在LT模型中，每个节点v会关联一个阈值θv表示该节点受影响的倾向，当来自活跃入邻居的权重之和超过θv时，节点v将被激活。已有的在线影响力最大化工作主要专注于IC模型和LT模型。

Chen W等人[14-15]首先将IC模型下的在线影响力最大化问题建模为带触发机制的组合多臂老虎机问题（CMAB with probabilistically triggered arms，CMAB-T）。在该模型中，社交网络中的每条边被视为一个基础臂，每次选择的种子节点集合为学习者选择的动作，种子节点集合的全部出边的集合被视为超级臂。基础臂的奖励的期望即该边的权重。随着信息在网络中的传播，越来越多的边被随机触发，其上的权重也可以被观察到。基于此模型，CUCB算法[14-15]即可被用于解决该问题。通过证得IC模型上的在线影响力最大化问题满足受触发概率调制的有界平滑性条件（triggering probability modulated condition），CUCB算法可以达到的累积懊悔上界，其中n、m分别表示网络中节点和边的数量[15]。

后续又有一些研究者对此工作进行了改进。Wen Z等人[68]考虑到社交网络中庞大的边的数量可能会导致学习效率变低，引入了线性泛化的结构，提出了IMLinUCB算法，该算法适用于大型的社交网络。该算法能达到的累积懊悔上界，其中d为引入线性泛化后特征的维数。Wu Q Y等人[69]考虑到网络分类的性质，将每条边的概率分解为起点的影响因子和终点的接收因子，通过此分解，问题的复杂度大大降低。该文献中提出的IMFB算法可以达到的累积懊悔上界。

上述研究工作均基于半强盗反馈，即只有被触发的基础臂的输出可以被学习者观察到。具体到在线影响力最大化问题，该反馈也被称为边层面的反馈，即所有活跃节点的每条出边的权重均可以被观察到。由于在实际应用场景中，公司往往无法获知具体哪个邻居影响到某用户购买商品，故该反馈是一种较为理想化的情况。节点层面的反馈是在线影响力最大化问题的另一种反馈模型，该反馈模型仅允许学习者观察到每个节点的激活状态。Vaswani S等人[70]研究了IC模型下节点层面反馈的情况，该工作分析了利用节点层面反馈估计每条边的权重与直接利用边层面反馈得到的估计值的差异，尽管两种估计的差值可以被约束，但该工作并没有给出对算法累积懊悔值的理论分析。

LT模型考虑了信息传播中的相关性，这给在线影响力最大化问题的理论分析带来了更大的挑战。直到2020年，Li S等人[71]研究了LT模型下的在线影响力最大化问题，并给出了首个理论分析结果。该工作假设节点层面的反馈信息，即传播过程每一步中每个节点的激活情况可以被观察到，并基于此设计了LT-LinUCB算 法，该 算 法 可 以 达 到的累积懊悔上界。此外，Li S等人还提出了OIM-ETC（OIM-explore then commit）算法，该算法可以同时解决IC模型和LT模型下的在线影响力最大化问题，达到了的累积懊悔上界。Vaswani S等人[72]还考虑了一种新的反馈类型，即信息在任意两点间的可达情况，并基于此反馈信息设计了DILinUCB（diffusionindependent LinUCB）算法。该算法同时适用于IC模型和LT模型，但其替换后的近似目标函数并不能保证严格的理论结果。

5 未来研究方向

组合在线学习问题仍有很多方面可以进一步研究和探索，具体如下。

● 设计适用于具体应用场景的有效算法。以在线影响力最大化问题为例，目前的研究工作多为通用的算法，基于TPM条件得到算法的累积懊悔上界。但实际应用场景中通常涉及更多值得关注的细节，如在线学习排序问题中用户的点击习惯、用户疲劳等现象，在线影响力最大化问题中信息传播的规律等。通用的算法往往难以全面考虑这些细节从而贴合具体的问题场景，因此针对具体问题场景设计出有效的算法，以及为这些问题证明其累积懊悔下界等仍然是值得研究的问题。

● 将组合在线学习与强化学习结合。MAB问题是强化学习的一种特例，CMAB是组合优化与MAB的结合，更进一步的问题是能否将这种结合推广到广义的强化学习领域，探索更广泛通用的组合在线学习框架，以涵盖更多的真实应用场景。

● 研究具有延迟反馈和批处理反馈的组合在线学习算法。实际应用场景中往往有更复杂的反馈情况，如在线排序学习问题中用户可能没有立即对感兴趣的项目进行访问，导致玩家行动与反馈之间有一定的时间差，即延迟反馈；有时广告供应商每隔一段时间才集中收集一次数据，即批处理反馈。在MAB问题中，针对这两种反馈方式的算法研究已取得一定的进展，在CMAB问题中，考虑这些复杂反馈形式的算法仍需继续探索。

● 深入研究分布式CMAB（distributed CMAB）。考虑多个玩家同时以相同目标选择超级臂的场景，玩家之间可以进行交流，但是每一轮每个玩家能共享的信息有限，玩家最终根据自己观察到的信息做出选择，并得到对应的独立的奖励值，最终每个玩家都会选择自己认为最优的超级臂。分布式探索的方法在MAB问题中已经有所应用和突破，但在CMAB场景中仍然需要更多的深入研究。

● 寻找更多的实际应用场景，以及在真实数据集上进行实验。已有算法可应用的数据集仍然有限，目前的研究工作多在人工数据集上进行实验，如何将算法应用到更多的真实数据集中并解决更多的实际问题，是具有重要实际意义的研究方向。

6 结束语

本文首先介绍了组合在线学习问题的定义及其基本框架——组合多臂老虎机问题，而后概括了此框架下的组合在线学习模型及经典算法。该问题有丰富的应用场景，本文重点介绍了在线排序学习和在线影响力最大化，详述了这两个应用场景下的研究进展。组合在线学习仍有许多值得深入探索的问题，本文最后对其未来研究方向做了进一步展望。