高海拔冻土区通风管路基管内风速及影响因素研究

宋正民，穆彦虎，马 巍，俞祁浩，栗晓林

（1.兰州理工大学土木工程学院，甘肃兰州730050；2.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州730000）

0 引言

在多年冻土地区，路基工程的修筑改变了下伏多年冻土原有脆弱的热平衡状态，由于冻土的冻胀、融沉特性，冻土路基存在普遍的工程病害［1-5］。对于公路路基而言，受沥青路面高吸热特性的影响［6］，路基下部多年冻土上限不断下降［7-8］、多年冻土温度不断升高［9-11］。随着全球气候的不断转暖，这一问题将会变得更加严峻。因此，针对多年冻土区的路基融沉问题，热管［12-14］、块石［15］、通风管［16-17］等一系列对流换热类主动“冷却路基”措施被广泛应用于冻土区路基工程的建设与维护，并起到了良好的作用［18-20］。

为研究热管、块石以及通风管的冷却降温效果及降温机理，现阶段已通过现场监测、数值模拟以及模型试验开展了大量的相关研究工作。Niu等［21-22］、Pei等［23］、Wen等［24］通过利用现场监测手段

研究了通风管、热棒以及块石护坡的冷却降温效果。在此基础上，Ma等［25-26］、Zhang等［27］、Mu等［28］利用数值模拟手段分析了通风管、块石路基的长期热状况的变化规律，Liu等［29］、Yu等［30］通过开展室内模型试验研究了块石护坡的冷却降温机理。依靠块石层内部的自然对流以及通风管内气流与管壁的强迫对流换热，可有效地降低路基土体的温度，达到保护路基下部多年冻土的效果。而通风管的管内风速是影响和决定通风管路基冷却降温的关键。同时，在青藏工程走廊风沙灾害日益严重的背景下，风沙的搬运、堆积将对通风管道及两侧护坡造成一定的堵塞，进而改变路基边坡块石层的边界类型、孔隙率以及通风管管内的通风效率等［31-32］。同时，随着公路的大尺度、高标准的设计要求的提升，由于路基尺度改变所引起的热收支状态的变化将对下部冻土地基产生影响。在高温多年冻土区，宽幅路基的修建导致基底吸热量增大20%以上，这将对路基下部多年冻土的稳定造成严重影响［33］。因此，为解决宽幅路基沥青路面的高吸热量对下伏多年冻土的影响，研究人员提出了分离式路基来解决幅宽热效应问题［34-35］。但分离式通风管路基受两幅路基间距的影响，后幅路基管内风速受前幅路基的遮挡导致管内风速有所降低，且随路基间距的减小，这一影响逐渐增强。目前，已有研究主要集中在通风管管内的对流换热过程对下部土体热状况的影响，而对于管内风速的影响因素及程度尚未有太多定量研究。因此，开展管内风速特征及其影响因素的研究对于通风管路基的强迫对流换热效果以及冻土路基工程的维护与运营十分必要。针对通风管路基管内风速的特征及影响因素，本文结合现场监测与数值模拟，开展了包括通风管埋设高度、管径、外伸长度以及两幅路基之间不同路基间距四种影响因素下的管内空气流速变化的特征研究。

1 研究方法

1.1 物理模型

为研究不同路基形式及通风管不同位置特征条件下的管内风速特征，以北麓河附近青藏公路沿线的试验路段为研究对象，研究了单幅路基在不同通风管管径、外伸长度、埋设高度以及两幅路基不同路基间距条件下的管内风速特征。物理模型分别如图1（a）、1（b）所示，其中单幅路基条件下，通风管管径（R）分别为0.4、0.5、0.6、0.7、0.8 m，通风管外伸长度（k）分别为0、0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8 m，通风管埋设高度（h）以0.25 m为高度差值，在路基高度为3 m条件下，通风管埋设高度为0.5～1.5 m；在路基高度为4 m条件下，通风管埋设高度为0.5～2 m；在路基高度为5 m条件下，通风管埋设高度为0.5～2.5 m；两幅路基之间的路基间距（L）为2、5、10、20、30、40、50 m。物理模型共分为空气区与路基区两部分，空气区高度为自天然地表以上30 m，宽度自路基两侧坡脚分别向外延伸60 m。

图1 路基风流场物理模型Fig.1 Physical models of wind flow over an embankment（a）and two separated embankment（b）

1.2 数学模型

在物理参数和边界条件的设定方面，根据青藏高原北麓河气象站、青藏高等级公路试验段现场实际情况和实测数据，选取大气压为57.7 kPa，空气密度0.737 kg·m-3，空气黏度1.75×10-5Pa·s，环境温度273 K，通风管管壁的粗糙度为0.003 m，地表粗糙度为0.14 m。模型的边界条件在左侧风入口处设置为速度入口，根据“综合幂次律”理论［36］，风速入口在边界KJ、EF处随高度的变化可简化为：

式中：vx y为入口边界沿高度的风速分布规律；vx10为10 m高度处环境风速，本文取10 m高度处环境风速为4 m·s-1，y为垂向高度。模型上部及两侧面采用对称（symmetry）边界，进口处采用速度入口（velocity-inlet）边界，出口处采用质量出口（outflow）边界，地表、路基边坡及顶部、通风管管壁选用固壁（wall）边界。

在不考虑热交换（即屏蔽能量方程），流体介质是空气，密度为常数的前提下，通过选择合适的离散格式可以加速收敛功能。本文采用高精度的二阶迎风格式对动量、湍动能和湍流耗散率等进行数值离散，同时考虑环境风速对路基的作用属于定常状态，选用SIMPLEC算法，且为控制计算过程中数值的失稳和发散，所以在计算中选择较小的松弛系数，本文采用压力欠松弛系数为0.2。为更好地模拟管道内流动，本文选用Realizablek-ε模型，该模型的输运方程如下［37-38］：

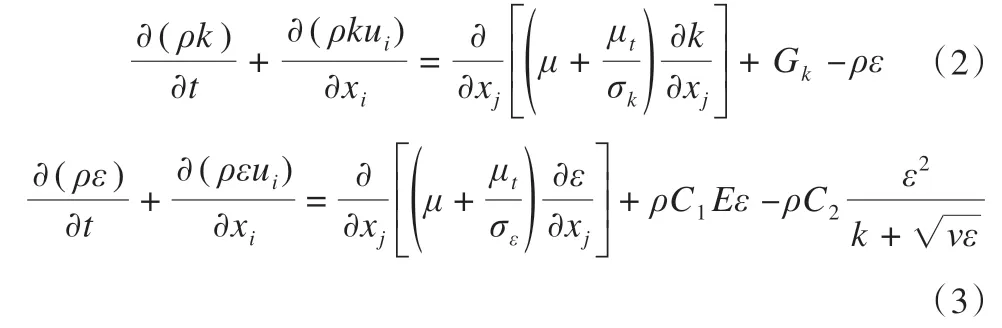
式中：

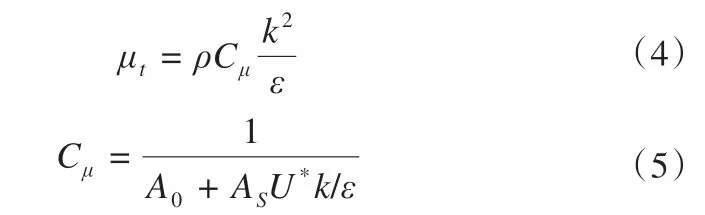
t为时间；ρ为空气密度；k为脉动动能；ui为空气在i方向的速度分量；xi、xj为空气沿i、j方向的位移；μ为空气动力黏度；μt为空气的湍流黏性系数；ν为动力黏度；σk的取值为1.0；Gk为由层流速度梯度而产生的湍流动能；ε为脉动动能耗散率；σε的取值为1.2；C2的 取 值 为1.9；C1=max（0.43，

1.3 模型及参数验证

利用青藏高原北麓河高速公路试验段风流场现场监测与数值模拟结果对比，开展本文数值模型和参数的验证。为掌握通风管内不同位置处风速特征，在试验段通风管中部及两侧出口处各安置一组风速、风向测试传感器，以获取通风管内不同位置处的风速与风向。通风管两侧的风速、风向传感器距离通风管管口0.85 m，通风管管径为0.4 m。试验段路基为东北—西南走向，路基高度为3 m，通风管埋设高度为1.2 m，如图2所示。

图2 北麓河试验通风管路基管内风速观测系统Fig.2 Observation system of wind flow over the ventilation duct experimental-built embankment at beiluhe basin

数值计算模型中风向与路基走向垂直，因此，通过选取现场风向监测装置监测到的风向为105°（路基走向为北偏东15°）时的管内风速与数值计算结果进行模型验证。为刻画通风管内不同位置处的风速大小，将通风管入口湍流区与出口湍流区每间隔0.2 m、中部平流区每间隔0.4 m设置一处风速监测断面，通过计算监测断面的风速平均值来刻画通风管内部不同位置处的风速大小，现场监测与数值模拟对比结果如图3所示。由图可知，通风管内部风速随环境风速的增加呈线性增加，斜率为0.5左右，但通风管进口处风速随环境风速的增加其斜率明显高于中部跟出口处风速。当10 m高度处环境风速为8 m·s-1时，通风管内最大风速差值可达0.18 m·s-1，约为环境风速的5%。

图3 数值模拟与试验工程实测数据对比Fig.3 Field measured and numerical simulated wind speed vs.environmental wind speed

2 模拟结果与分析

2.1 单幅通风管路基管内风速模拟

2.1.1 单幅通风管路基条件下管内风速分布特征受通风管管径、外伸长度以及埋设高度的影响通风管内部的风速分布有所差异，为了解管内不同位置处的风速分布特征，本文通过利用数值模拟的方法来进行管内风速分布的差异性分析。图4给出了路基高度为3 m、路面宽度为13 m、通风管外伸长度为1.3 m、10 m高度处环境风速为4 m·s-1且风向与路基走向垂直条件下管内风速分布云图。根据管内不同位置处的风速波动情况将管内风速分为入口湍流区（I）、中部层流区（II）、出口湍流区（III）三个区域。在入口湍流区（I），上升气流冲撞通风管上管壁，导致I区内的空气流动主要以湍流为主，纵向波动范围、波动幅度最大；随着气流的继续深入流动，空气粒子不断与管壁碰撞造成能量不断损失，紊流经过充分发展后呈现较为平稳的层流状态（II区），空气的运动轨迹近似直线；在出口湍流区，管内空气受管口气压剧烈变化的影响，空气的湍流流动、波动强度相对II区明显增大，纵向波动幅度有所增加。

图4 管内风速分布云图Fig.4 Wind speed field in ventilation duct

由图4可知，当10 m高度处环境风速为4 m·s-1时，II区范围可占据通风管内部的80%左右，随环境风速的提升，II区范围有所减小，当环境风速达到10 m·s-1时，II区范围仍占据50%以上，故本文以II区特征风速为研究目标，开展通风管不同管径、不同外伸长度以及不同埋设高度三种工况条件下管内风速的特征研究。

2.1.2 不同管径条件下管内风速分布特征

通风管管径的增加可以加大管口处空气的入流面积，并且随着管径的增加，进管口处风速受路基迎风坡遮挡效应造成的减速效果也有所差异。因此，为探究通风管管径对管内风速的影响效果，以路基高度3 m、通风管外伸长度1.3 m、通风管埋设高度1.2 m为标准，针对不同通风管管径条件下管内空气流动的差异性进行分析。图5给出了10 m高度处环境风速为4 m·s-1时，管内风速与管径的关系曲线。由图可知，随着通风管管径的增加，管内风速呈抛物线形式增加，最大可达2.58 m·s-1，约为同一高度下环境风速的85%。当管径达到0.6 m时，管内风速增加不再明显。通过对管内风速模拟可知，受管壁粗糙度影响，管径的增加导致近壁区黏滞层的低风速范围与管中平流层高风速范围均有所上升，当管径达到0.6 m后，二者之间的增量幅度近似相等，管内风速不在随管径的增加而明显提升。

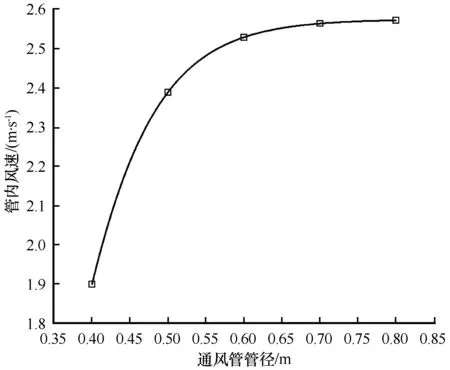
图5 不同管径条件下管内风速变化Fig.5 Wind speed in ventilation duct with different diameters

为探究管径增加所造成的通风管内不同位置处的流速差异，通过数值计算给出了环境风速为4 m·s-1时不同通风管管径内的最大风速差值曲线（图6）。由图可知，随管径的增加，管内最大风速差值呈线性减小，斜率约为-0.175。受管壁粗糙度的影响，入口湍流区空气撞击管壁所造成的动能损失较大，速度明显降低，管内空气逐渐由湍流发展为层流。而层流状态下管内风速受管壁粗糙度的影响较小，动能损失较低。因此，随管径的增加，管内流速整体上升。入口湍流区的湍动强度逐渐减小，动能损失逐渐降低，由此导致通风管内部不同位置处的风速分布差异逐渐减弱。

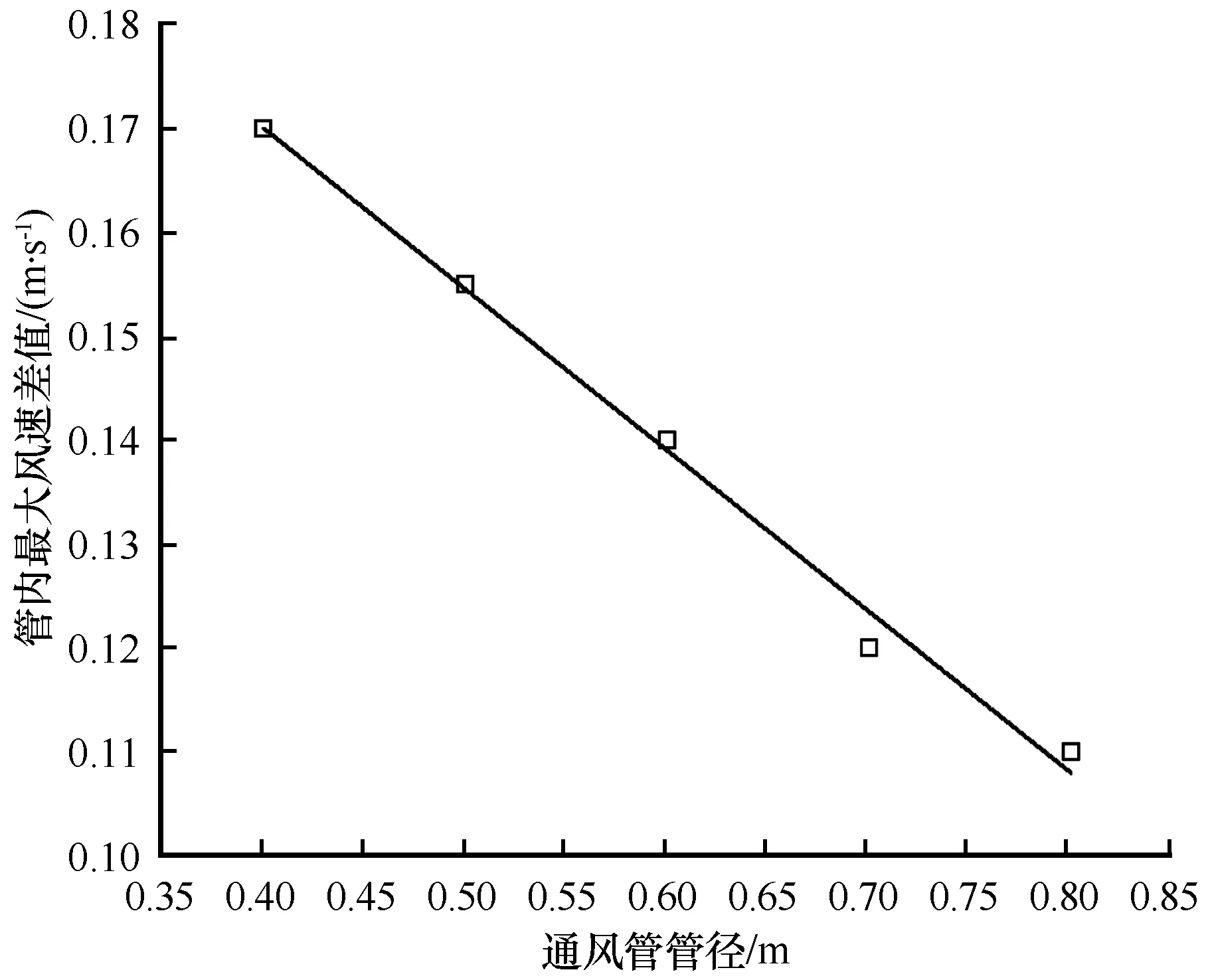
图6 不同管径条件管内最大风速差值分布曲线Fig.6 Maximum wind speed difference in ventilation duct with different diameters

2.1.3 通风管不同外伸长度条件下管内风速分布特征

管内风速的大小主要受两侧气压差值及温度影响，在不考虑温度变化的情况下，管口两侧气压差值将决定管内风速的大小，而不同通风管外伸长度将导致通风管两侧的气压差值有所差异。为研究通风管外伸长度对管内风速的影响程度，图7（a）给出了通风管管径为0.4 m、埋设高度为1.2 m、10 m高度处环境风速为4 m·s-1的条件下，通风管管中风速与通风管外伸长度之间的关系曲线。由图可知，当环境风速保持不变时，随通风管外伸长度的增加，管内风速基本保持不变，且在外伸长度为0.6 m时达到最大值。当环境风速为2 m·s-1时，不同通风管外伸长度条件下，管内风速最大差值仅为0.02 m·s-1，但随着环境风速的提升，这一差值逐渐提升，当环境风速为14 m·s-1时，这一差值可达0.3 m·s-1。图8给出了不同通风管外伸长度下管口两侧的气压云图，由图8（a）、8（b）可知，当10 m高度处环境风速为4 m·s-1时，随着通风管外伸长度的增加，通风管两端的气压差值逐渐增大，两侧管口处气压差值由通风管外伸长度为0 m时的3.2 Pa增加到通风管外伸长度为2.8 m时的3.8 Pa。当10 m高度处环境风速为14 m·s-1时，两侧管口处气压差值由通风管外伸长度为0 m时的26 Pa增加到通风管外伸长度为2.8 m时的32 Pa［图8（c）、8（d）］。由此可见，当环境风速较低时，通风管两侧的气压差值受通风管外伸长度的影响较小，随环境风速的增加，这一影响逐渐增强。

图7 不同环境风速下通风管外伸长度与管内风速关系曲线Fig.7 Extension length of ventilation duct vs.wind speeds in ventilation duct under different environment wind speed

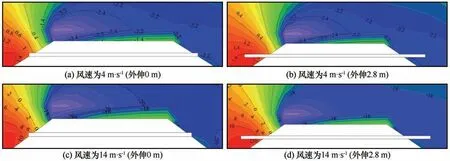
图8 10 m高度环境风速4 m·s-1通风管外伸长度0 m（a）、2.8 m（b）及10 m高度环境风速14 m·s-1通风管外伸长度0 m（c）、2.8 m（d）下通风管路基周边静压云图Fig.8 Air static pressure field around the ventilation duct embankment under the environmental wind speed of 4 m·s-1 at 10 m height，0 m（a），2.8 m（b）and 14 m·s-1 at 10 m height，0 m（c）and 2.8 m（d）

图9 （a）～9（c）给出了通风管外伸长度为0 m、1.6 m、2.6 m三种条件下的管口空气流线图（图中流线颜色越深代表空气流速越大）。由图可知，随通风管外伸长度的增加，通风管入口处速度流线弧度减小，管内空气流速受迎风坡遮挡效应造成的减速效果逐渐降低，通风管入口处的流线夹角（α）由外伸长度0 m时的16°～18°降低至通风管外伸长度为2.8 m时的2°～3°。并且随通风管外伸长度的增加，管内风速受管壁粗糙度的影响越来越明显，近壁处动能损失逐渐增加。因此，受管壁粗糙度、迎风坡遮挡效应、通风管管口两侧气压差值三方面的混合影响，管内风速随通风管外伸长度的增加变化不明显。

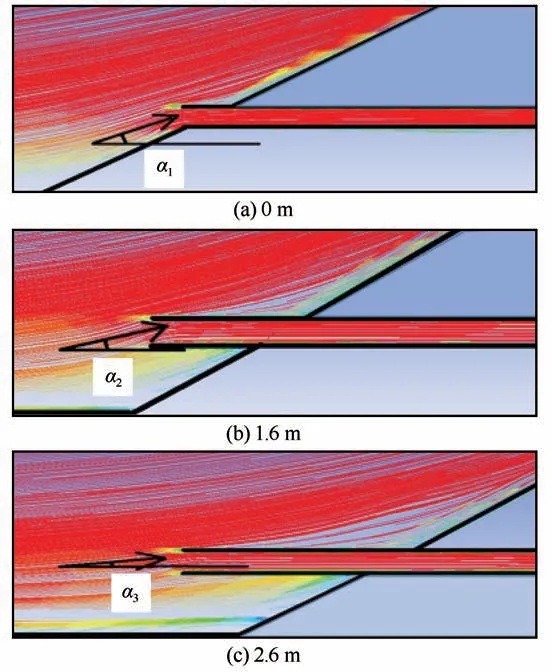
图9 不同通风管外伸长度下管口流线示意图Fig.9 Schematic diagram of streamline under different ventilation duct extension lengths of 0 m（a），1.6 m（b）and 2.6 m（c）

2.1.4 通风管不同埋设高度条件下管内风速分布特征

路基高度的增加会加剧阴阳坡效应，导致路基下部聚热效应更加明显。因此，为更大程度发挥通风管的对流换热作用，以此来带走因路基高度增加导致边坡吸收的更多热量，通风管的安装高度不宜过高。本文以路面宽度13 m，通风管管径0.4 m，通风管外伸长度1.3 m，通风管埋设高度0.5 m为起始高度，以路基高度的一半为埋设上限，对不同路基高度条件下管内风速进行数值模拟计算，结果如下。

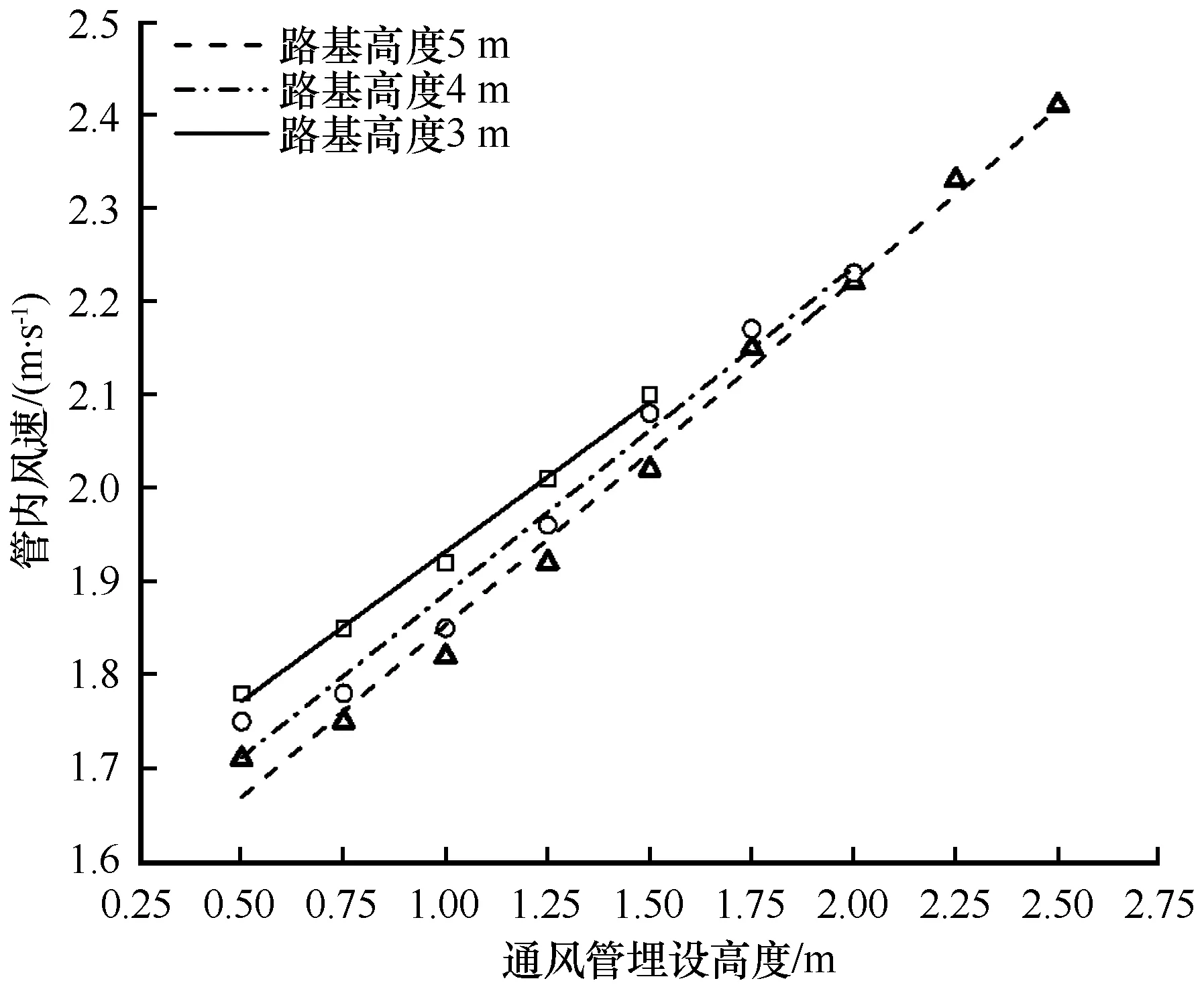
图10 不同路基高度、通风管高度条件下管内风速Fig.10 Wind speed in ventilation duct vs.buried depth of the ventilation duct under different embankment thickness

随路基高度的提升，同一高度条件下坡前风速逐渐下降，管内风速受迎风坡的扰动更加明显。通风管埋设高度的增加导致进风口处流线夹角逐渐增加，但随通风管埋设高度的提升，管口处环境风速也相应增加，最终导致管内风速呈线性增加趋势。当通风管高度为0.5 m时，3 m高路基较5 m高路基管内风速差值约为0.1 m·s-1，且这一差值随通风管高度的增加逐渐减小，当通风管高度达到2 m时，管内风速受路基高度的影响逐渐削弱，不同路基高度条件下管内风速逐渐趋向一致。以往研究表明，当路基高度超过4 m后，坡前扰动区的高度范围差异逐渐减小。因此，当通风管高度达到2 m时，管内风速受路基高度的影响不在增加。

2.2 分幅通风管路基管内风速模拟

利用青藏高原高海拔、高风速、低气温的特点，在路基土体内部埋设通风管道可有效地增加路基土体与空气的接触面积，通过管道内空气与管壁间的强迫对流换热来减少路基土体传入路基下部的热量，进而实现抬高多年冻土上限，维持路基土体稳定的目的，是一种积极主动的降温措施。但目前管内空气流速的研究相对较少，为探究不同气候条件下环境风速的改变所导致的两幅路基管内风速之间的差异性，首先通过对路基两侧不同位置处风速监测与模拟结果进行验证，再此基础上结合管内实测风速与数值模拟结果，在两者均达到较高耦合度的情况下开展分幅条件下两幅路基管内风速的差异性分析研究。据2018年8月份北麓河试验段最新的管内风速测试点资料显示，3 m高度处的平均风速为3.46 m·s-1，本文对于通风管内部风速特征研究选用通风管管径为0.4 m，外伸长度1.3 m，距地面高度1.2 m，3 m高度处环境风速为1～8 m·s-1进行。路基两侧风流场的实测模拟结果如图11所示。

图11 路基坡脚不同距离处数值模拟与现场实测风速沿高度分布结果对比Fig.11 Field measured and numerical simulated wind speeds vs.height at different distances away from the embankment slope foot

由图12可知，前幅路基管中平均风速可达3 m高度处环境风速的41%～58%。且随环境风速的增加，管内风速呈线性增加。环境风速对第二幅路基的影响显著，当路基间距为2 m时，由于路基间距较小，前管与后管之间间距仅为3 m，因此受路基迎风坡的影响，在两幅路基之间与后幅路基背风坡后形成低压涡旋区，涡速最高值出现在靠近地表跟路基边坡处，且从压力云图13可知，两处涡旋压力基本相等，因此进入后管的气流主要来源于前管中冲出的高速湍流，且受涡旋影响，后幅路基管内风速最大仅为0.2 m·s-1。随着两管之间间距的增加，前管冲出的高速湍流对后管的影响越来越小，当路基间距达到5 m时，由静压云图可知，后幅路基通风管两侧气压值大致相同，但受前幅路基的遮挡，后幅路基坡前主要为低速涡流，而后幅路基坡后为高速涡流，导致后幅路基背风坡后涡旋的一部分涌进通风管，造成管内空气逆流。

图12 不同路基间距下后幅路基管内风速Fig.12 wind speed in ventilation duct under different spacing of the two separated embankments

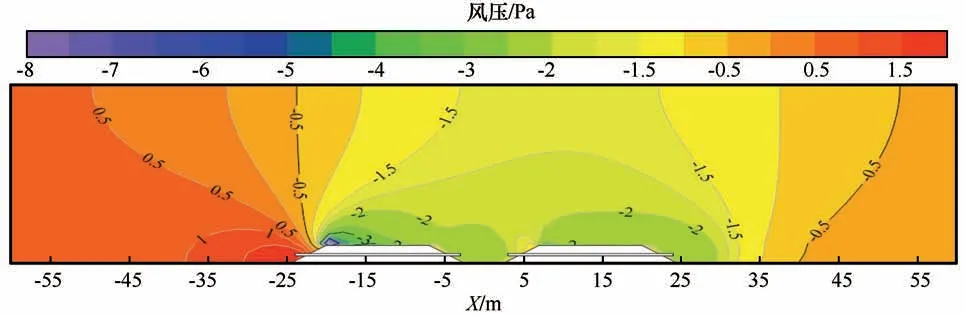
图13 路基周边风压云图Fig.13 Air static pressure field around the embankment

背风坡后涡旋容易造成坡后风沙聚集，导致背风坡处风积沙涌入管内，堵塞通风管，减弱通风管降温效果。当路基间距大于5 m后，随着路基间距和环境风速的不断增加，后幅路基管内的风速逐渐升高。当路基间距一定时，随环境风速的增加，前幅路基与后幅路基之间的管内风速差值呈增加趋势，受背风坡后涡旋影响，随环境风速的增加，背风坡后涡旋的横向尺寸逐渐增大。且由模拟结果可知，当环境风速小于8 m·s-1时，路基间距达到50 m，后幅路基管内风速最小可达前幅路基管内风速的89%，且随路基间距的增加后幅路基管内风速增量逐渐减小，在考虑现场修建对地表的破坏以及占用面积的情况下，可近似认为当两幅路基的路基间距达到50 m后，两幅路基的管内风速差异可忽略不计。

3 结论

通过利用现场监测与数值模拟相结合的方法，开展了高海拔冻土区通风管路基在不同通风管管径、外伸长度、埋设高度以及两幅路基不同路基间距条件下管内风速分布特征研究，结论如下：

（1）通风管路基管内风速受迎风坡及管壁粗糙度的影响可以划分为3个区域；即入口扰动区（I）、中部平流区（II）、出口湍流区（III）。且管内空气流动主要以II区为主，对于通风管路基而言，其降温机制主要依赖于管内空气与路基土体的强迫对流换热，因此，掌握管内风速的大小（尤其是II区风速）至关重要。

（2）在路基高度、通风管外伸长度、通风管距地高度一定时，管内风速随管径的增加呈抛物线型增加，当管径达到0.6 m时，管中风速基本保持不变，与0.4 m管径相比，管内风速提升可达0.6 m·s-1。当环境风速保持不变时，随管径的增加，管内最大风速差值逐渐减小，管内风速整体趋向一致。

（3）通风管外伸长度的不同导致通风管进风口处流线弧度、两侧管口处气压值都不相同，但由模拟结果可知，受管壁粗糙度、两侧管口气压差以及进风口处流线弧度三方面的共同影响下，管内风速随通风管外伸长度的增加变化不大。

（4）管内风速受通风管埋设高度影响较大，随埋设高度的增加，管内风速呈线性增加，但受路基高度的影响，其增加幅度有所差异。当通风管埋设高度超过2 m后，管内风速受路基高度的影响不在增加。因此，结合通风管的冷却降温效果与管内风速的变化，野外通风管的布设高度不应高于2 m.

（5）分离式路基管内风速受环境风速、路基间距的影响最为明显，当路基间距小于5 m时，后幅路基受前幅路基的遮挡作用，管内风速较小（接近0）并出现逆流现象。当路基间距达到10 m后，后幅路基管内风速随环境风速的增加呈线性增加。当路基间距达到50 m后，后幅路基管内风速可达前幅路基管内风速的89%，可认为后幅路基管内风速受前幅路基的遮挡所造成的管内风速下降可忽略不计。