基于衍生多边形的混合坐标
2021-09-19李亚娟邓重阳
黄 茹,李亚娟,邓重阳
(杭州电子科技大学理学院,浙江 杭州 310018)
1827 年,MÖBIUS[1]首次提出2D 重心坐标的概念:平面三角形内任意一点可由三角形的顶点线性表示,该线性组合的系数就是三角形内该点的重心坐标。1975 年,WACHSPRESS[2]首次提出多边形顶点数量大于 3 的重心坐标(wachspress coordinates,WC),但该重心坐标仅对凸多边形有明确的定义。2003 年,FLOATER[3]提出2D 的均值坐标(mean value coordinates,MVC),该坐标对任意多边形有明确的定义,且在多边形内部光滑。2005 年,FLOATER 等[4]提出3D 的均值坐标,该坐标可表示四面体内部的一点关于四面体顶点的凸组合。2006 年,LANGER 等[5]提出球重心坐标(spherical barycentric coordinates),在球体上定义平面重心坐标系中的任意重心坐标,并给出球体上一点相对于给定球面三角形顶点的重心坐标。2007 年,JOSHI 等[6]利用调和坐标(harmonic coordinates,HC),将重心坐标的定义扩展到任意维度,且即使在强凹的情况下重心坐标仍然具有非负性。调和坐标没有具体的表达式,而是通过求解Laplace方程得到。2008 年,HORMANN 和SUKUMAR[7]提出最大熵坐标(maximum entropy coordinates,MEC),通过牛顿法求解凸优化问题计算得到。最大熵坐标可应用于平面内任意多边形,且具有非负性。2008 年,LIPMAN 等[8]提出格林坐标(Green coordinates,GC),利用cage 的顶点与面的法向信息,通过格林第三等式推导得到,在空间变形中具有良好的保形性。2011 年,MANSON 等[9]提出正Gordon-Wixom 坐标(positive Gordon-Wixom coordinates,PGWC),在任意多边形内具有非负性,但其光滑性会受到多边形边界光滑性的限制。2014 年,ZHANG 等[10]提出局部重心坐标(local barycentric coordinates,LBC)。LBC仅依赖于一部分控制顶点,且通过基于全变分的凸约束优化计算得到。2016 年,ANISIMOV 等[11]提出细分重心坐标(subdividing barycentric coordinates,SBC),将被广泛使用于构造曲面的细分算法应用于构造重心坐标。2017 年,ANISIMOV等[12]利用混合重心坐标(blended barycentric coordinates,BBC),对任意多边形先进行约束Delaunay 三角剖分,在剖分得到的三角形上计算均值坐标,再通过合适的混合函数计算得到。2019,TAO 等[13]提出新的数值计算方法计算局部坐标,与之前的局部坐标[10]相比提高了计算效率,但未满足非负性。2020 年,DENG 等[14]提出迭代坐标(iterative coordinates,IC),将初始多边形投影至单位圆,并通过迭代圆上的多边形,直至计算均值心坐标为非负,最后通过回代得到关于初始多边形的重心坐标。
本文在三角网格的内部将三角形衍生得到点多边形、边多边形和面多边形,提出基于衍生多边形的混合坐标,继承了HC,LBC 和IC 的局部性和非负性,通过实例还表明在多边形内部光滑。
1 衍生多边形

1.1 点多边形

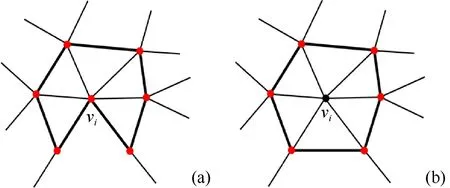
图1 点多边形示意图((a)边界点的点多边形;(b)内部点的点多边形) Fig.1 Diagram of the point polygon ((a) The point polygon of the boundary point;(b) The point polygon of the inner point)
1.2 边多边形

1.3 面多边形

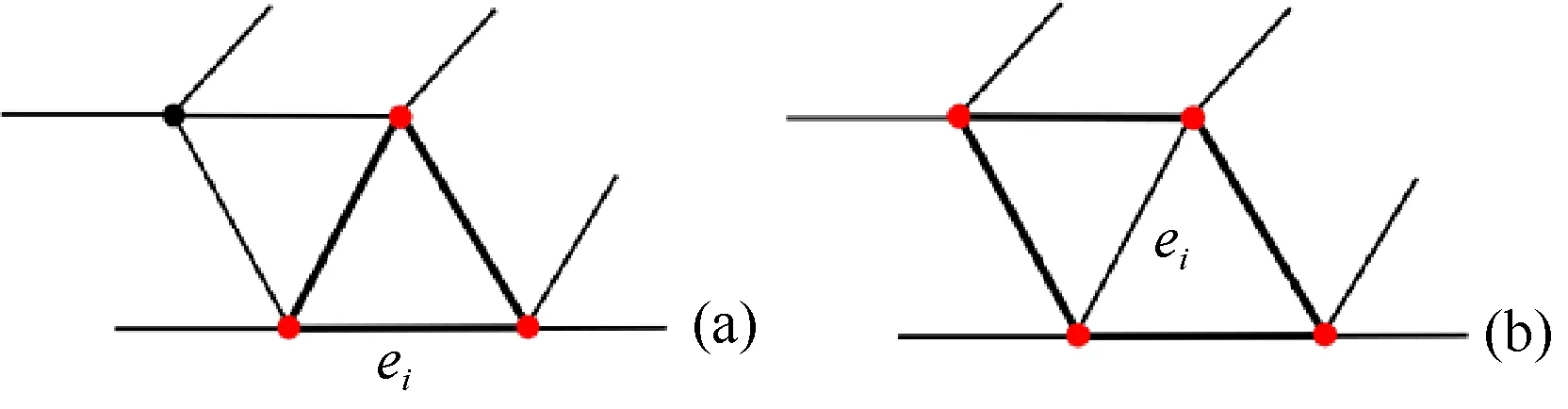
图2 边多边形示意图((a)边界边的边多边形;(b)内部边的边多边形) Fig.2 Diagram of the edge polygon ((a) The edge polygon of the boundary edge;(b) The edge polygon of the inner edge)
2 基于衍生多边形的混合坐标算法

HC,LBC 和IC 均满足上述性质,本文提出的基于衍生多边形的混合坐标继承了其局部性和非负性,并且在选取合适的混合系数后还满足光滑性。
2.1 混合系数的选取

2.2 基于衍生多边形的混合坐标


3 实例分析

由文献[6,10,14]可知HC,LBC 和IC 满足非负性,则Ak和均满足非负性,故Bk也满足非负性。又因为混合系数为非负的,因此由式(4)可知基于衍生多边形的混合坐标具有非负性。
因为衍生子多边形的顶点关于初始多边形的重心坐标仅与部分初始多边形的顶点相关,即存在λi=0。又因为点p关于衍生子多边形顶点的重心坐标仅与部分衍生子多边形的顶点相关,即存在可知点p通过第k个衍生子多边形得到关于初始多边形的初始混合坐标具有局部性,故基于衍生多边形的混合坐标具有局部性。
图3 比较了同一多边形的同一顶点处不同重心坐标的等高线与伪彩图,其中图3(d)~(f)分别为使用IC,HC 和LBC 计算衍生多边形的顶点关于初始多边形顶点的重心坐标,再使用IC 计算点关于衍生多边形顶点的重心坐标。如图3 所示,与均值坐标、迭代坐标、调和坐标相比,基于衍生多边形的混合坐标具有更好的光滑性。
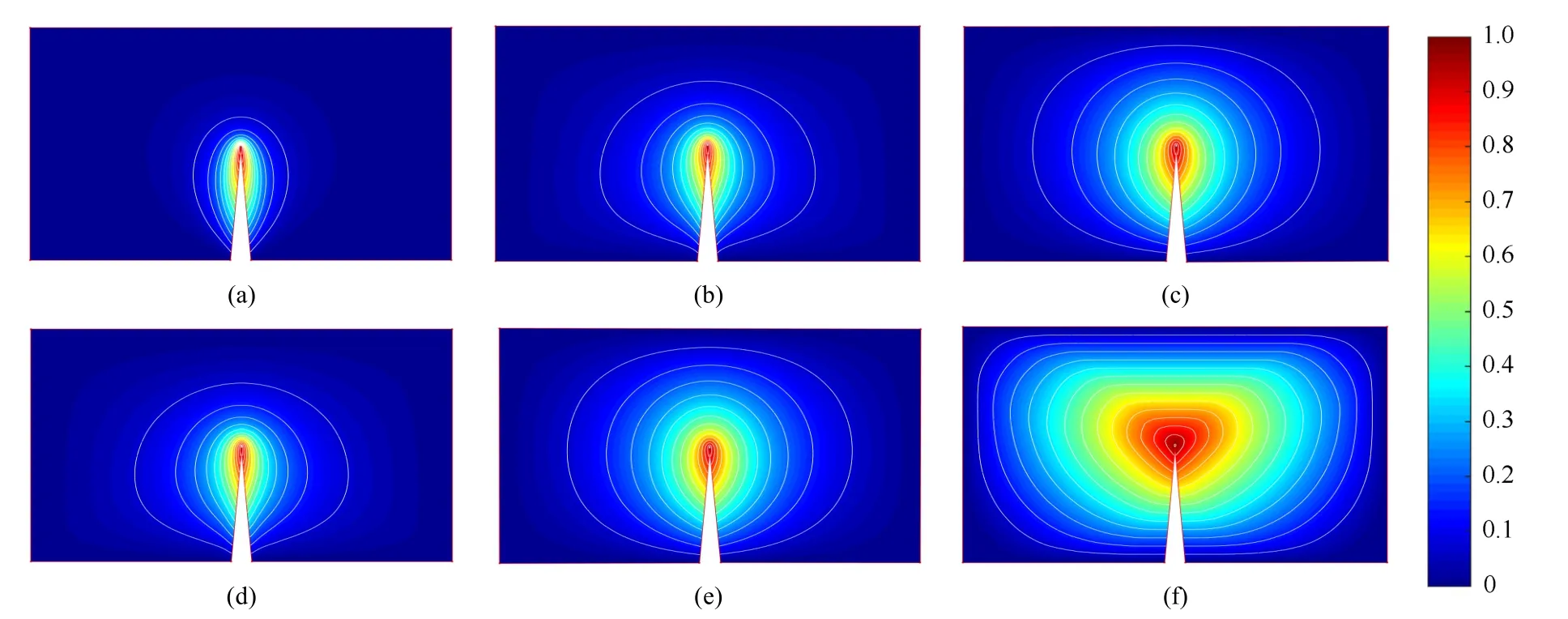
图3 不同重心坐标的等高线与伪彩图((a)均值坐标;(b)迭代坐标;(c)调和坐标;(d) IC_IC 混合坐标;(e) HC_IC 混合坐标;(f) LBC_IC 混合坐标) Fig.3 Iso-high lines and pseudo-color drawings of different center of gravity coordinates ((a) Mean value coordinates; (b) Iterative coordinates;(c) Harmonic coordinates;(d) IC_IC Blended coordinates; (e) HC_IC Blended coordinates;(f) LBC_IC Blended coordinates)
图4(a)~(f)分别展示了六边形、七边形、八边形、九边形、十边形和Woody 的同一顶点处的等高线与伪彩图。图4 中从上到下分别使用IC,HC 和LBC计算衍生多边形的顶点关于初始多边形顶点的重心坐标,再使用IC 计算点关于衍生多边形顶点的重心坐标,绘制对同一个多边形的同一顶点的等高线与伪彩图,并将其简称为 IC_IC,HC_IC,LBC_IC。其中IC_IC,HC_IC 使用MATLAB 的PDE工具箱进行三角化,LBC_IC 使用LBC 使用的Triangle 进行三角化。

图4 不同多边形的等高线与伪彩图((a)六边形;(b)七边形;(c)八边形;(d)九边形;(e)十边形;(f) Woody) Fig.4 Iso-high lines and pseudo-color drawings of different polygons ((a) Hexagon;(b) Heptagon;(c) Octagon; (d) Enneagon;(e) Decagon;(f) Woody)
将同一多边形的初始化三角形网格的数量取相近数量,每个面取100 个采样点,最终计算这些采样点的时间,见表1。实例表明本文提出的基于衍生多边形的混合坐标具有好的局部性、非负性和光滑性。由图4(a)~(d)可观察到LBC_IC 的局部性比HC_IC 和IC_IC 的更好,对于相同的点处的等高线LBC_IC 显然与更少的顶点相关。由图4(c)~(f)可观察到HC_IC 的光滑性比LBC_IC,IC_IC 的更好。由表1 可观察到IC_IC 的计算时间最短。
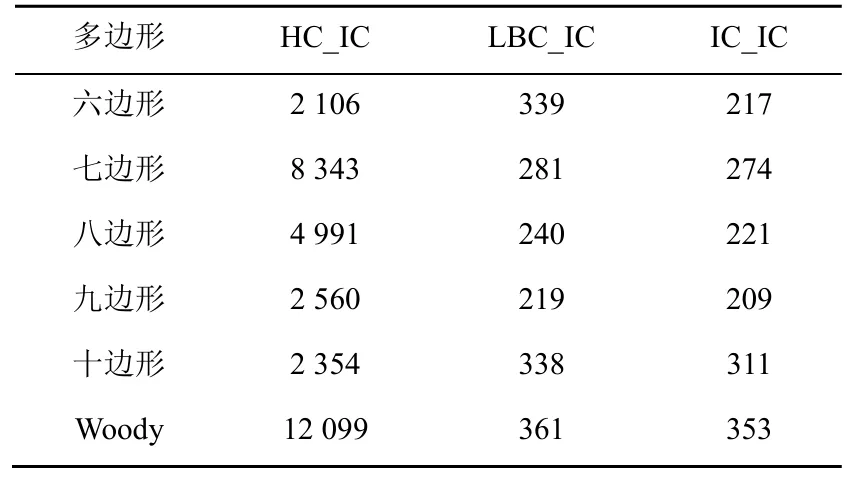
表1 不同多边形的计算坐标的时间(s) Table 1 The time of calculate barycentric coordinates for different polygons (s)
4 结束语
本文首先给出衍生多边形的定义,利用三角网格定义点多边形、边多边形和面多边形。基于衍生多边形利用HC,LBC 和IC 计算点关于初始多边形的初始混合坐标。再使用合适的混合系数,得到基于衍生多边形的混合坐标。其中,点多边形PPʹ对应的混合系数为边多边形EPʹ对应的混合系数为(λ0+λ1)2,(λ1+λ2)2,(λ2+λ0)2;面多边形EPʹ对应的混合系数为
因为衍生多边形的结构简单且可经过少许迭代次数便可使均值重心坐标为正,因此对于相同的多边形,基于衍生多边形的混合坐标在计算过程中需要迭代的次数少于IC,减少了计算量。今后工作的重点是将二维的基于衍生多边形的混合坐标推广到三维,并寻找更合适的混合系数,使得在不改变光滑性的前提下达到更高的连续性。
