基于八叉树SBFE网格的混凝土细观模型生成方法

杜成斌 郑伟康

摘要： 为更准确地反映混凝土材料过渡区的几何形状和材料性质，通过基于图像的八叉树网格加密技术对混凝土结构过渡区进行局部网格加密。采用平衡八叉树划分算法进行空间单元剖分，首先基于最大单元尺寸的体素，将结构离散为若干子单元，然后根据颜色强度均匀性标准进一步细分单元，直到单元中的每个体素均满足颜色强度阈值条件，最后根据2 ∶1原则形成八叉树网格。由于三维比例边界有限元网格允许存在悬挂節点，因此生成的模型相对常规有限元模型具有求解域离散简单、网格过渡快、单元模式少等优点。八叉树网格与具有半解析特点的三维比例边界有限元法相结合，可非常方便地求解混凝土类非均质材料的应力变形，且具有计算工作量少、精度高的特点，为混凝土类非均质材料的力学建模和计算提供了新途径。数值算例验证了所提出方法的正确性和可行性。

关 键 词： 八叉树; 混凝土; 细观模型; 网格过渡; 比例边界有限元法

中图法分类号：  TU528.01

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2021.08.027

0 引 言

混凝土材料作为水工及民用建筑中应用最广泛的材料之一，其力学性能一直以来都是研究的热点。受观测技术和研究方法的限制，传统的混凝土材料力学理论建立在宏观均质假设的基础之上，然而真实的混凝土材料是由多相材料组合而成，其在宏观层次上力学性能的表现实质是细观组成结构的体现，因此混凝土材料在细观层次上的非均质特性受到了越来越高的重视[1]。

基于对混凝土细观各相相互作用模型的假设和求解方法的不同，混凝土细观力学模型大致可分为三大类[2]：基于有限元法（Finite Element Method，FEM）的连续介质细观力学模型、基于离散元法的非连续介质细观力学模型以及基于FEM-离散元耦合法的细观力学模型。唐欣薇等[3]基于连续介质细观力学模型，研究了细观各相组分的非均质性对混凝土力学性能的影响，马怀发等[4]采用背景网格法建立了大坝混凝土三维细观力学数值模型，刘卫东[5]等采用了基于离散元法的细观力学模型，研究了集料粒径和试件尺寸对沥青混合料开裂行为的影响。然而，在上述细观模型分析中，由于各相几何形状的复杂性，增加了建立FEM网格的难度，传统的FEM网格因不允许有悬挂节点，常常在材料分区附近出现很密的网格，导致模型计算成本高、计算效率低等问题。

随着计算机技术的发展，四叉树/八叉树网格因其划分速度快、主单元模式少等优点被逐渐应用到细观网格模型的建立中。丁胜勇等[6]基于平衡四叉树网格加密技术实现了混凝土细观模型的局部网格加密。刘兆松等[7]基于数字图像处理建立了混凝土细观FEM模型。但是由于四叉树/八叉树网格生成过程中会产生悬挂节点，使得该方法与FEM的结合受到了限制。Song和Wolf提出的比例边界有限元法[8]（Scaled Boundary Finite Element Method，SBFEM），其只需对求解域的边界进行离散，使空间计算维度降低了一维，且不需要基本解。SBFEM单元可以是任意多面体（多边形），它允许存在悬挂节点，国内外学者将其与四叉树/八叉树网格划分算法相结合进行结构分析。Ooi等[9-10]提出了一种基于四叉树-多边形比例边界有限元法，模拟了混凝土结构的裂纹扩展。邹德高[11]等提出一种增强八叉树与SBFEM结合的方法来对工程实例进行应力分析。目前，大多数的研究都侧重于平面问题，将八叉树与SBFEM结合对空间混凝土细观模型的研究鲜有见到。

为更准确反映混凝土的细观结构，本文采用基于图像的平衡八叉树网格加密技术对混凝土砂浆和骨料的过渡区进行局部网格加密，建立了基于八叉树SBFE网格的混凝土细观力学模型。首先介绍了三维SBFEM以及平衡八叉树的概念，然后详细给出了平衡八叉树网格划分的具体步骤，最后通过数值算例验证所提方法的正确性和可行性。

1 三维比例边界有限元法

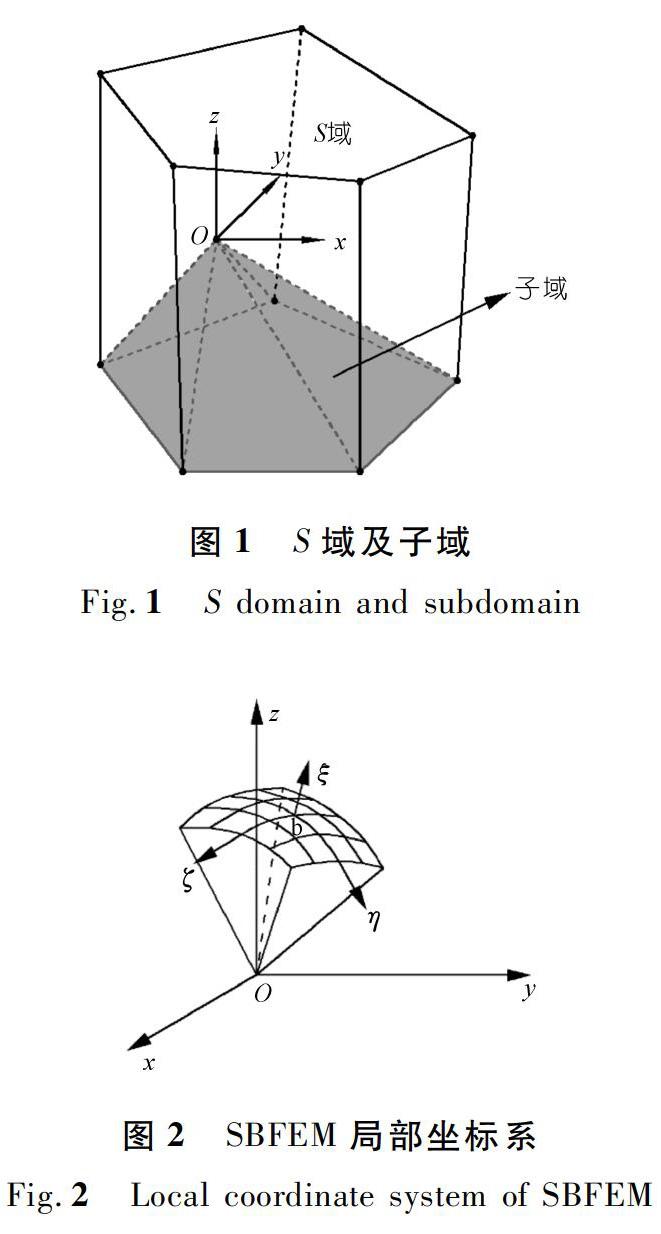
在三维SBFEM中，其基本单元称为S域，可以是任意多面体形状。在每一个S域中设置一个比例中心O，比例中心可以在对所有边界可见的前提下设置在S域内的任意位置，它与边界节点的连线将S域划分为若干个子域，如图1所示。以比例中心O（x0，y0，z0）为原点建立相应的局部坐标系（ξ，η，ζ），如图2所示。三维SBFEM的坐标系包括一个径向坐标ξ以及两个环向坐标η和ζ。在比例中心处，ξ=0;在边界处，ξ=1;S域内的其他位置取为0<ξ<1。环向坐标与二维FEM局部坐标类似。

在子域内，任意一点在笛卡尔坐标系下的坐标（x，y，z）可由比例边界局部坐标（ξ，η，ζ）表示如下：

x ξ，η，ζ =x0+ξ  N  η，ζ {x}-x0

（1）

y ξ，η，ζ =y0+ξ  N  η，ζ {y}-y0

（2）

z ξ，η，ζ =z0+ξ  N  η，ζ {z}-z0

（3）

式中： N （η，ζ）为插值形函数矩阵;（x0，y0，z0）为比例中心的坐标;{x}，{y}，{z}为边界上的节点坐标集。

每个子域内的位移函数可以通过插值函数表示为

u  ξ，η，ζ = N u η，ζ  u  ξ

（4）

式中： u （ξ）为子域内的径向位移函数。

对位移函数进行微分计算，可以得到子域内的应变函数：

ε = Lu  ξ，η，ζ

= B 1 η，ζ  u  ξ ，ξ+ 1 ξ  B 2 η，ζ  u  ξ

（5）

式中： L 为微分算子; B 1（η，ζ）， B 2（η，ζ）为应变位移矩阵，只与子域的几何形状有关，可由节点坐标信息求出。

将应变函数代入本构方程可以求得子域内的应力函数：

σ  = Dε

= DB 1 η，ζ  u  ξ ，ξ+ 1 ξ  DB 2 η，ζ  u  ξ

（6）

根据虚功原理[12]，可以推导出关于位移的三维比例边界有限元静力平衡方程：

E 0ξ2 u  ξ ，ξξ+ 2 E 0- E 1+ E T1 ξ u  ξ ，ξ+  E T1- E 2  u  ξ + P  ξ =0

（7）

式中： P （ξ）为外力项; E 0， E 1， E 2为系数矩阵项。

最终，通过舒尔分解法[13]求得其位移解的形式如下：

u  ξ = φ 11ξ-  S 11+0.5 I   c 1

（8）

式中： φ 11为位移模态的特征向量; S 11为位移模态的特征值; c 1为位移模态的积分常数。式（8）表明SBFEM的解在径向是解析的，它决定了其解的半解析特征。

一旦位移求出，将其代入式（5）和式（6）即可求出应变和应力。

SBFEM除了具有半解析的特点，它在网格上可以允许悬挂节点，因为它是在边界上离散的，某边上的悬挂节点相当于是边界离散增加了插值点，处理起来非常方便。例如图3，对于一个简单的四边形边界面单元ABCD，AB边上存在一悬挂节点P，可以认为是边界面ABCD增加了一个插值点，将边界面APBCD视为一个五节点单元，这样就保证了P点的位移协调性。这一点给网格过渡带来了很大的方便。

2 基于图像的八叉树网格划分算法

基于图像的网格划分方法主要有三大类[14]：第一类需在划分前定义各相的边界;第二类直接基于图像的像素正方形或体素正六面体建立均匀网格;第三类为基于像素/体素的四叉树/八叉树网格划分算法。总体来说，前两类方法的网格生成较为简单，但生成的网格数量多，刚度矩阵以及数值积分的计算量大，而第三类方法可以快速实现不同尺寸单元的过渡，具有更好的适应性。

2.1 八叉树数据结构

八叉树是一种采用递归思想将三维空间的节点分解为互为关联的8个子节点的层次化树状数据结构[15]。它的每个节点代表一个立方体的体积单元，每个节点有8个子节点，将8个子节点代表的体积单元加在一起就等于父节点的体积。八叉树以三维空间中整个待划分区域的最小外接正方体为根单元，递归地把它分成8个子单元，直到所有单元都满足规定条件即停止划分。图4即为一个简单的八叉树单元产生过程。

平衡八叉树结构是在普通八叉树结构的基础上要求相邻层次之间单元尺寸满足2 ∶1的平衡原则，即限制其任意相邻单元之间所处的层次差不大于1。平衡八叉树结构严格限制了相邻单元尺寸变化的梯度，其最大的优点在于减少了主单元模式的数量。

2.2 平衡八叉树网格的生成步骤

采用STL格式的3D图像，图5（a）是一个8×8×8体素的3D图像，包含了一个1体素的灰点和一个2×2×2体素的灰点，设置最大单元尺寸为amax=4×4×4体素，最小单元尺寸为amin=1体素，颜色强度阈值t即为一个单元中每个体素之间所允许的最大颜色强度差值，取t=0。利用平衡八叉树对其进行网格划分主要有以下几个步骤：

（1） 用一个最小外接立方体的包围盒圈定目标模型，得到一个8×8×8体素的根单元。

（2） 根据最大单元尺寸amax将根单元均分为8个4×4×4体素的子单元，如图5（b）所示。

（3） 根据颜色的不均匀性，将不满足颜色强度均匀性标准（t=0）的每一个立方体单元递归划分为8个大小相等的子单元。含有2×2×2体素灰点的单元通过一次细分得到8个2×2×2体素的子单元，含有1体素灰点的单元则经过两次细分得到7个2×2×2体素的子单元和8个1体素的子单元，如图5（c）所示。

（4） 按照2 ∶1平衡原则进一步划分单元，得到图5（d）中的平衡八叉树网格。

2.3 基于八叉树的S单元

通过平衡八叉树分解后得到的单元都是立方体单元，将比例中心设置在立方体的几何中心得到S域。SBFEM的离散化只需在S域的表面进行，對于八叉树单元的一个表面，根据其四条边上是否存在悬挂节点或表面中心点，考虑单元格的旋转后总共只有7种八叉树表面单元节点配置模式，如图6所示。对于两个几何相似的单元，用于分析的单元矩阵是相同的或成比例的，单元模式减少可以很大程度地减少计算量。

与FEM网格单元相比，基于八叉树的S单元主要有以下优点：

（1） 允许存在悬挂节点，保证了相邻八叉树单元之间的位移协调性。

（2） 表面离散比FEM要求的体积离散更简单。

（3） 可以实现粗细网格的快速过渡，建模效率高。

（4） 主单元节点配置模式少，计算成本低。

3 数值算例

3.1 悬臂梁弯曲

图7为一受剪切力作用的均质悬臂梁，截面是边长a=10 mm正方形，梁长L=40 mm。其中一端（z=40 mm）固定，另一端（z=0 mm）自由且受到y轴负向的剪切力τy=10 MPa。悬臂梁弹性模量为E=25 GPa，泊松比为υ=0.25，不计重力。

3.1.1 竖向位移和正应力

采用基于图像的八叉树算法建立SBFEM网格模型，图片大小为256×256×256体素，每个体素代表一个边长为0.156 25 mm（最小外接立方体边长与图片边长的比值）的立方体单元。设置单元大小为32×32×32体素（边长5 mm），总共得到32个立方体单元。取梁上表面中轴线AB上的任意一点C，将其计算结果与解析解[16]对比。由于边界处存在应力集中现象，故应力结果只取梁中间某段结果进行对比，如图8～9所示，图中横坐标为LAC/LAB，图8的纵坐标为竖向位移uy，图9的纵坐标为σz/τy。由图可知，本文结果与解析解几乎完全一致，从而验证了所提出方法计算结果的正确性。

3.1.2 计算精度对比

对于上述悬臂梁结构，取不同自由度下的网格模型。为了避免应力集中的影响，分别用SBFEM和FEM计算AB中点（0，5，20 mm）的正应力值σz，并与文献[16]中求得的解析解进行对比，其结果见表1。由表1可知，当结构自由度接近时，SBFEM的应力结果更加接近解析解，并且自由度为8 019时的SBFEM结果比自由度为421 443时的FEM结果更加精确。

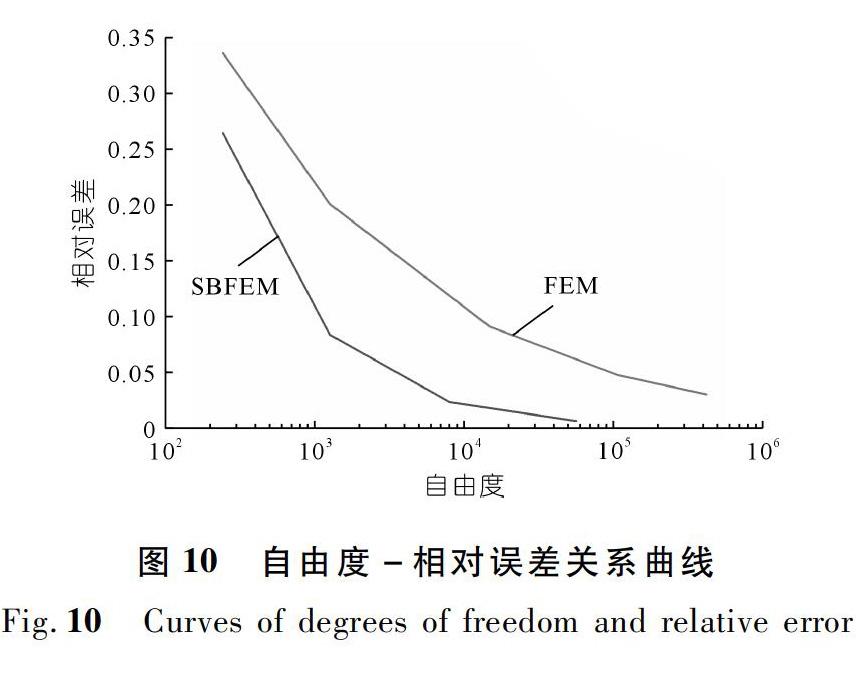
图10给出了两种方法下自由度与应力结果相对误差的关系曲线。由图10可知，两种方法的相对误差都随着结构自由度的增大而减小，SBFEM的相对误差整体上都低于FEM。当自由度大于8 000时，SBFEM的相对误差基本维持在2%以下，而FEM则超过了5%，说明SBFEM在较少的自由度就能达到较高的精度。

综上所述，在结构自由度接近时，本文所提方法比FEM有着更高的计算精度，并且能在自由度更小的情况下满足计算精度要求。

3.2 3D混凝土细观模型

如图11（a），对于3D三级配混凝土非均质结构，体积表征单元（Representative Volume Element，RVE）的边长取a=300 mm。考虑混凝土是由球形骨料、砂浆和界面组成的三相材料，将骨料最外层单元视为界面单元，基于图像颜色进行各相材料分区。界面层的生成步骤如下：

（1）  对于每一个随机骨料模型，以球心为基准，缩小半径2 mm（这个主要根据界面层厚度而定），生成两个球心位置相同骨料半径不同的新的随机骨料模型A。

（2） 通过布尔运算，对上述两个骨料模型取差集，形成一组球壳模型B，作为边界层。

（3） 对B的体素赋上与骨料和砂浆不同的颜色强度值（例如150），作为第三种材料分区。

（4） 将A和B的体素组合进行平衡八叉树网格划分。

（5） 重新定义材料区间，例如，[0，85]区间内为材料1（砂浆）;[86，170]区间内为材料2（骨料）;[171，255]区间内为材料3。

（6） 赋上相应的材料参数生成含有界面单元的随机骨料模型。

其中，骨料的弹性模量为Eagg=50 GPa，泊松比为υagg=0.16;水泥砂浆的弹性模量为Ecem=30 GPa，泊松比为υcem=0.22;界面层的弹性模量Eb=20 GPa，泊松比为υb=0.18[17]。为按富勒级配曲线[18]，三级配骨料的特征粒径分别取20，40，80 mm，采用蒙特卡罗法生成骨料体积含量分别为20%、30%和40%的混凝土随机骨料模型，其骨料粒径分布和颗粒数由表2给出。

以骨料含量为40%的RVE为例，基于平衡八叉树建立混凝土细观网格模型，图片像素大小设置为256×256×256体素，每个体素代表一个边长为1.171 875 mm的立方体。最大和最小单元尺寸分别取16×16×16体素（边长18.75 mm）和4×4×4体素（边长4.687 5 mm），划分后得到的网格如图11（b），其单元数为214 397，自由度数为758 490。在FEM模型中，采用六面体单元（C3D8R），单元尺寸取为4.687 5 mm，生成的FEM网格如图11中（c）所示，其模型的单元数为262 144，自由度数为823 875。

由图11可以看出，想要实现最小网格尺寸相同（SBFEM：4×4×4体素;FEM：4.6875 mm），FEM模型（背景网格法）需要全局加密网格，而基于八叉树的SBFEM模型只需在材料交界处进行局部网格加密，减少了18%的单元数和8%的自由度数，节约了计算成本，可更好地实现混凝土骨料与砂浆之间的粗细网格过渡。

对上述混凝土细观模型进行单轴压缩数值试验。模型底面为固定端，其余表面自由。在模型顶面施加轴向压力σy0=50 MPa。取模型的一条轴向线AB作为特征线（见图11（a）），C点为AB上任意一点，C点的轴向位移uy和轴向应力结果σy如图12和图13所示。由图可知，基于八叉树SBFE网格生成的混凝土细观模型与FEM混凝土细观模型的模拟结果较为吻合，由此说明所提方法在实际混凝土非均质结构分析中的可行性。

4 结 语

基于平衡八叉树网格加密技术对混凝土材料过渡区进行局部网格加密，实现了粗细网格的快速过渡，在不失精度的情况下，改善了常規FEM在材料过渡区网格锯齿状的不足，更合理地反映了混凝土材料过渡区的真实状态。基于图像进行网格剖分可望把工程师从繁杂的网格剖分工作中解脱出来，充分利用先进的计算技术，提高建模效率。同时，SBFE网格允许存在悬挂节点，给网格过渡带来了极大的方便。平衡八叉树剖分对求解域表面进行离散更加简单便捷，可以降低计算成本，为混凝土类非均质结构力学计算提供了一种新的途径。

参考文献：

[1]  张楚汉，唐欣薇，周元德，等.混凝土细观力学研究进展综述[J].水力发电学报，2015，34（12）：1-18.

[2] 侯翔宇.混凝土细观力学仿真模拟研究进展综述[C]∥天津大学、天津市钢结构学会.天津：第十七届全国现代结构工程学术研讨会论文集，2017：4.

[3] 唐欣薇，张楚汉.混凝土细观力学模型研究：非均质影响[J].水力发电学报，2009，28（4）：56-62.

[4] 马怀发，陈厚群，吴建平，等.大坝混凝土三维细观力学数值模型研究[J].计算力学学报，2008（2）：241-247.

[5] LIU W D，GAO Y，HUANG X M.Effects of aggregate size and specimen scale on asphalt mixture cracking using a micromechanical simulation approach[J].Journal of Wuhan University of Technology（Materids Science Edition），2017，32（6）：1503-1510.

[6] 丁胜勇，邵国建，李昂，等.基于四叉树网格加密技术的混凝土细观模型[J].建筑材料学报，2015，18（3）：375-379.

[7] 刘兆松，娄宗科，丁聪，等.基于数字图像处理的混凝土细观有限元建模[J].人民长江，2012，43（19）：56-59.

[8] SONG C M，WOLF J P.The scaled boundary finite-element method-Alias consistent infinitesimal finite-element cell method-For elastodynamics[J].Computer Methods in Applied Mechanics and Engineering，1997，147（3-4）：329-355.

[9] GUO H，OOI E T，SAPUTRA A A，et al.A quadtree-polygon-based scaled boundary finite element method for image-based mesoscale fracture modelling in concrete[J].Engineering Fracture Mechanics，2019，211：402-441.

[10]  OOI E T，NATARAJAN S，SONG C M，et al.Crack propagation modelling in concrete using the scaled boundary finite element method with hybrid polygon-quadtree meshes[J].International Journal of Fracture，2017，203（1-2SI）：135-157.

[11] ZOU D G，CHEN K，KONG X J，et al.An enhanced octree polyhedral scaled boundary finite element method and its applications in structure analysis[J].Engineering Analysis with Boundary Elements，2017，84：87-107.

[12] DEEKS A J，WOLF J P.A virtual work derivation of the scaled boundary finite-element method for elastostatics[J].Computational Mechanics，2002，28（6）：489-504.

[13] SONG C M.A matrix function solution for the scaled boundary finite-element equation in statics[J].Computer Methods in Applied Mechanics and Engineering，2004，193（23-26）：2325-2356.

[14] 黃宇劼.基于XCT图像和比例边界有限元法的混凝土细观断裂模拟[D].杭州：浙江大学，2017.

[15] 戴愿桥，廖敦明，陈涛，等.基于八叉树的自适应网格剖分算法研究[C]∥中国机械工程学会、铸造行业生产力促进中心.苏州：2017中国铸造活动周论文集，2017.

[16] BISHOP J E.A displacement-based finite element formulation for general polyhedra using harmonic shape functions[J].International Journal for Numerical Methods in Engineering，2014，97（1）：1-31.

[17] 夏晓舟.混凝土细观数值仿真及宏细观力学研究[D].南京：河海大学，2007.

[18] 王菁，武亮，糜凯华，等.三级配混凝土二维随机多边形骨料模型数值模拟[J].人民长江，2015，46（11）：71-75.

（编辑：郑 毅）

引用本文：

杜成斌，郑伟康.基于八叉树SBFE网格的混凝土细观模型生成方法

[J].人民长江，2021，52（8）：179-185.

A concrete mesoscopic model generation method based on octree scaled

boundary finite element mesh

DU Chengbin，ZHENG Weikang

（ College of Mechanics and Materials，Hohai University，Nanjing 211100，China ）

Abstract：

In order to accurately reflect the geometric shape and material properties of the concrete transition area，the local mesh of the concrete structure transition area was densified by image-based octree mesh densification technology.We use the balanced octree partition algorithm to divide spatial elements.Firstly，the structure was discretized into several sub-element based on the voxels of the maximum element size.Then，the elements were further subdivided according to the color intensity uniformity standard until every voxel in the unit met the color intensity threshold condition.Finally，the octree grid was formed according to the 2：1 principle.Compared with the conventional finite element model，the three-dimensional scaled boundary finite element method allowed the existence of hanging nodes，so that the generated model had the advantages of simple domain solution，fast mesh transition and fewer element modes.Combined with the semi-analytical three-dimensional scaled boundary finite element method，the octree mesh was very convenient to solve the stress and deformation of concrete heterogeneous materials with less calculation workload and high precision，which provided a new way for the mechanical modeling and calculation of concrete heterogeneous materials.Numerical examples demonstrated the correctness and feasibility of the proposed method.

Key words：

octree;concrete;mesoscopic model;grid transition;scaled boundary finite element method