基于Matlab/Simulink的超声速自由射流试验系统建模分析

孙顺利 李纲 芦海洋

摘 要： 为实现对关键指标舱压的动态变化过程仿真， 基于Matlab/Simulink对某超声速自由射流试验系统的关键物理过程建模， 并将仿真结果与试验结果比较分析。该模型的仿真舱压与试验舱压的曲线变化规律一致， 试验状态稳定段的仿真舱压与试验舱压的误差在1 kPa以内， 喷管出口仿真静压值与试验静压值也小于1 kPa， 同时还具备模拟启动迟滞现象和启动后的舱压与喷管进口总压的正线性关系现象的能力。对比分析结果表明， 该Simulink建模方法能有效模拟超声速自由射流试验系统舱压的动态变化。

关键词：自由射流试验;  舱压;  超声速喷管;  引射;  扩压

中图分类号：    TJ763; V231.3  文献标识码：    A  文章编号：1673-5048（2021）04-0076-06

0 引  言

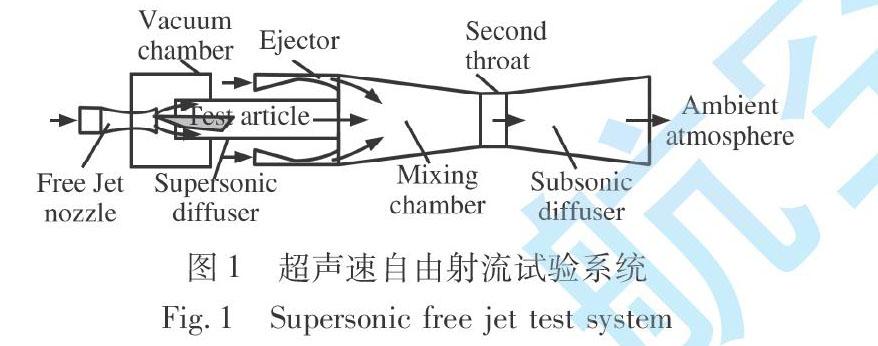
超声速自由射流试验系统可在地面模拟高空飞行条件， 常用于冲压发动机的考核试验， 是研制冲压发动机的基础设施之一， 吸引了大量科研机构进行研究[1-4]。其工作原理是加热后的高压气体通过自由射流喷管达到超声速状态， 对高空舱内的气体产生引射抽吸作用， 使高空舱内的压力下降， 同时自由射流喷管出口气流充分膨胀， 获得满足冲压发动机进气道进口前的均匀马赫数和压力分布， 发动机试验件放置在该均匀流场内。超声速气流与冲压发动机的排气混合后， 在下游扩压器减速增压作用和主动引射器气流抽吸作用下， 经亚声速扩压器排出到大气环境。 关键部件和结构关系如图1所示。

对于超声速自由射流试验系统， 高空舱模拟压力（简称舱压）指标直接反映自由射流喷管的启动状态， 是试验人员判断试验系统工作状态的重要指标。文献[5]采用一维理论方法计算了某型超声速试验系统的性能， 指出舱压最小值由扩压器壅塞和射流膨胀现象决定， 且试验件堵塞会导致舱压升高;  文献[6]采用试验方法研究了真空引射的启动与不启动现象的運行机理和影响因素;  文献[7-8]综合运用理论分析、 试验和数值仿真方法深入研究了超声速试验系统的启动特性、 负载匹配和压力恢复性能等， 获得设备结构和气动参数对舱压的影响;  文献[9-10]研究了超声速引射器启动迟滞现象的影响因素和预测方法。上述文献大都侧重于单个稳定状态点的性能指标分析， 对舱压指标的连续动态变化也多采用试验方法， 而采用理论方法进行研究的较少。本文借鉴文献[11]提出的作用力平衡的研究方法和文献[12]中的建模方法， 基于Matlab/Simulink对某超声速自由射流试验系统的关键物理过程建模， 实现对试验系统舱压的连续动态变化过程仿真， 并与试验结果比较分析， 验证建模方法的可行性。

1 模型建立

1.1 高空舱数学模型

根据质量守恒定律， 高空舱控制体流入流出的质量流量总变化等于高空舱内的质量变化， 进而可计算出高空舱内的质量， 再通过理想气体方程计算出舱压：

mc=mcini+∫（m·leak- m·s）dt=PaRTVc+∫（m·leak- m·s）dt（1）

Pc=mcVcRT （2）

高空舱流入流量主要是高空舱补气造成， 高空舱补气过程简化为限流孔节流绝热过程， 当舱内和舱外的压差越大， 则补气量越大， 可得补气流量[12]： 航空兵器 2021年第28卷第4期

孙顺利， 等： 基于Matlab/Simulink的超声速自由射流试验系统建模分析

m·leak=

CfAPa2γRT（γ-1）PcPa2γ-PcPa）γ+1γ   PcPa≥2γ+1γ+1γ-1

CfAPaγRT2γ+1γ+1γ-1

PcPa<2γ+1γ+1γ-1（3）

式中： mc和mcini为高空舱内气体的实时和初始质量;  m·leak和m·s为高空舱补气和流出的质量流量;  Pa和Pc为大气压和高空舱实时静压;  R， T和γ为气体常数、 静温和比热比;  Vc为高空舱容积;  Cf和A为补气孔流量系数和面积。  其中补气孔面积和流量系数可根据试验和调试数据进行修正。

1.2 自由射流引射数学模型

高空舱流出流量由自由射流引射数学模型决定，射流喷管出口的静压P1n大于喷管出口舱压P1s（舱压等于二次流静压）， 即当P1n>P1s， 喷管出口气流等熵膨胀：

P2n=P1nν1nν2nγ=P1nAfnAshd-As-Ablkγ（4）

二次流气流等熵压缩：

P2s=P1s1+γ-12M22s1+γ-12M21sγγ-1（5）

两股气流在下游某点达到压力平衡（P2n=P2s）， 形成气动喉道As：

As=Ashd-Ablk-AfnP1sP1n1+γ-12Ma22s1+γ-12Ma21sγγ-11γ （6）

式中： Ablk为试验件等堵塞面积;  γ为比容;  当P1n≤P1s时， 喷管出口气流不膨胀， 气动喉道为扩压器管道面积减去自由射流喷管出口面积， 即As=Ashd-Afn， 此处不包含发动机试验件和台架， 因而不存在堵塞面积。

（1）当As处达到壅塞时， Ma2s=1， 可得二次流的最大质量流量m·smax：

m·smax=γR2γ+1γ+1γ-1PcTcAs （7）

通过As与A1s的等熵膨胀关系， 可得二次流进口的马赫数Ma1s和静压P1s， 最后得到作用力Fsmax：

Fsmax=P1sA1s（1+γMa21s）（8）

需要注意的是， 当As≥0时， m·smax≥0， 此时二次流流出高空舱控制体外;  而当As<0时， m·smax<0， 射流喷管气流在扩压器内欠膨胀， 此时二次流流入高空舱控制体内， 舱压升高， 这是模拟当自由射流喷管启动后， 舱压随自由射流喷管进口总压升高而升高的线性关系现象[13-14]的关键方法。

（2）当As处未壅塞时， 假设二次流流量在正负最大二次流流量之间， 即-m·smax

Ma1s-m·sA1sPtγRTt1+γ-12Ma21sγ+12（γ-1）=0（9）

采用二分法迭代求解， 得亚声速解Ma1s（0～1）。 由等熵膨胀关系得静压P1s：

P1s=Pc1+γ-12Ma21s-γγ-1  （10）

最后得二次流作用力Fs：

Fs=P1s（Ashd-Afjn）（1+γMa21s）（11）

式中： 1， 2， mix为扩压器不同截面;  n， s为自由射流和二次流;  Ma， Pt， Tt为马赫数、 总压和总温。

1.3 自由射流喷管气动数学模型

拉瓦尔喷管出口气流静压和马赫数受进口总压和出口背压的共同影响， 存在9种情况[15]。 根据仿真建模需要可简化为以下3种情况：

（1）当π1

P1n=Pc（12）

Ma1n=2γ-1（1-（P1n/Pt）γ-1-γ）（13）

（2）当π2≤Pc/Pt≤π1， 喉道壅塞， 喷管扩张段内存在正激波， 喷管出口靜压为舱压， 由喉道壅塞条件和质量守恒定律可得

P1n=Pc（14）

Ma1n=1γ-1+

1γ-12+2γ-12γ+1γ+1γ-1PtP1n2AtA1n2（15）

式中： At和A1n为喷管喉道和出口面积。  出口背压与进口总压的临界压比π1与π2的计算方法见文献[16-17]。

（3）当Pc/Pt<π2， 喉道壅塞， 扩张段内全部为超声速， 出口马赫数为喷管名义马赫数Mafn， 由喷管喉道和出口面积比决定。 由等熵膨胀关系式可得出口静压：

Ma1n=Mafn（16）

P1n=Pt（1+γ-12Ma2fn）-γγ-1（17）

最后将喷管出口马赫数Ma1n和静压P1n带入下式， 得到质量流量和作用力：

m·n=Ma1nA1nPtγRTt/（1+γ-12Ma21n）γ+12（γ-1）（18）

Fn=P1nA1n（1+γMa21n）（19）

1.4 超声速扩压器扩压过程数学模型

扩压器出口压力主要基于质量、 能量和动量守恒对自由射流和二次流的气流混合求解出口参数：

m·n+m·s=m·mix（20）

m·nCpnTtn+m·sCpnTts=m·mixCpmixTtmix（21）

P1nA1n+P1sA1s-PmixAmix-Ff=m·mixvmix-m·nvn-m·svs（22）

式中： Cp， v为定压比热容和速度。

假设管道摩擦力Ff=0， 作用力的计算式为

F=PA+m·v=PA+PRTAv2=PA（1+γγRTv2）=

PA（1+γMa2）（23）

替换式（22）中相关项后可得

F1n+F1s=Fmix（24）

最后可得到扩压器出口的质量流量、 总温和作用力。

质量流量计算式为

m·=PAMaγRTt（1+γ-12M2）（25）

式（25）与式（23）中静压P相等， 联立后得

P=m·AMγRTt（1+γ-12M2）=FA（1+γM2） （26）

经整理得关于M2二次方程式：

AM4+BM2+C=0（27）

式中： A，B，C分别表示代替二次方程系数。

由于混合过程具备真实物理意义， 因此B2-4AC≥0， 式（27）在数学意义上必然存在实数解：

M2=-B±B2-4AC2A（28）

式中： 取+号时为超声速解， 当该值为负数， 则不存在超声速解;  取-号时为亚声速解， 对应于存在超声速解时的正激波波后亚声速解或者不存在超声速解时的亚声速解。 当特殊情况B2-4AC=0， 此时恰好M=1。

最后可得混合后的扩压器出口静压Pout， 考虑到由于在超扩段内通常不是理想正激波， 而是以多道斜激波的激波串使压力恢复， 因此存在压力损失， 考虑超声速扩压器内非理想正激波压力损失修正的的波后静压：

Pmix-crt=Pmix（1-σγmix-12Ma2mix）γmixγmix-1 （29）

考虑亚声速扩压器内的膨胀作用的出口压力：

Pout=Pmix-crt（1+ηdγmix-12Ma2mix）γmixγmix-1（30）

式中： σ为超声速段内的压力恢复系数;  ηd为扩压效率。

1.5 动态仿真的原理和基本流程

高空舱流出流量由自由射流引射数学模型决定， 对应于二次流m·s， 其数学模型建立过程如图2所示。 动态仿真模型流程如图3所示。其关键算法是计算出正确的二次流流量， 当混合后的扩压器出口压力大于或等于大气压时， 最大的二次流流量即为二次流流量， 当混合后的出口压力小于大气压时， 则二次流量介于正最大二次流流量和负最大二次流流量之间， 通过二分法求得实际二次流流量， 使出口压力等于大气压。

图4是H=6 km， Ma=2.5工况下， 二次流最大值m·smax和实际值m·s的对比。当m·s

2 仿真与试验结果对比分析

图5～6是自由射流试验系统的两次试验及仿真结果。需要说明的是， 此高度范围不需要打开下游的引射器， 实际模拟高度以试验结果的静压为准。喷管出口静压的测量点位于喷管出口内壁面。

对比图5～6， 可见仿真舱压和试验舱压的变化规律基本一致， 对喷管进口总压参数的变化具有较好的响应跟随性， 当自由射流喷管总压和舱压稳定后， 仿真舱压与试验舱压的误差在1  kPa以内，  该Simulink模型可以准确模拟试验系统稳定后舱压值。

另外， 两次试验仿真中， 当自由射流喷管总压到目标值时（图5（b）中17～21 s， 图6（b）中13～50 s）， 补气孔面积差异导致舱压高于或低于相应模拟高度， 当补气孔面积足够大时， 舱压无法抽到模拟高度附近;  补气孔面积足够小时， 舱压远小于模拟高度。因此， 补气孔面积是舱压调节的关键参数。

当舱压受补气孔面积影响而没有与实际模拟高度一致时， 自由射流喷管出口静压的试验值和仿真值均达到模拟高度， 二者误差在1 kPa以内， 喷管出口达到名义马赫数为2.5。 结果表明在舱压高于和低于喷管出口静压的两种条件下， 该Simulink模型也可以准确模拟试验系统稳定后的喷管出口静压条件。因此， 仿真模型通过准确计算的喷管出口舱压和静压， 根据斜激波理论和普朗特迈耶理论可计算喷管出口的均匀流场的菱形区面积[18]， 获得发动机试验件的安装位置和有效试验时间。

舱压与自由射流喷管进口总压变化关系对比如图7所示。在启动过程中， 舱压先随自由射流喷管进口总压降低， 当舱压达到最低时， 随自由射流喷管总压呈线性关系增加， 与文献[14]中描述一致。在图7（a）中， 仿真结果也显示舱压会随自由射流喷管总压变化时出现启动迟滞现象。 与试验结果相比， 图7（a）中的仿真最小启动压力（A点）与试验最小启动压力（B点）相差在70 kPa左右， 仿真和试验的最小保持启动压力（C点）基本吻合， 可见仿真结果较好地捕捉到启动迟滞现象的两个关键试验点。对于自由射流喷管进口阀门开启和关闭的动态过程中， 仿真舱压与试验舱压的啟动迟滞幅度存在较大差异， 原因是： （1）自由射流喷管进口阀门的关闭时间比开启时间要短， 造成喷管进口总压在下降时的速度比上升时快， 进而在计算二次流流量时， 喷管进口阀门关闭时的实际二次流量较大， 并且容易受到负最大二次流量的限流（m·s=-m·smax）， 而喷管进口阀门开启时的实际二次流量小， 并且不易造成正最大二次流量的限流（m·s<+m·smax）， 结果可以在图4中14～16 s和23～24 s时间段观察到。（2）查阅文献[19]， 启动迟滞现象普遍存在亚声速与超音速转变过程， 如进气道和引射器的启动与不启动状态转变过程。 启动时由亚声速转变为超声速需要突破正激波的压力损失， 因而需要更高的进口总压， 而从超声速转变为亚声速时不启动状态则压力损失较小， 特别是对于存在二次喉道的情况， 这种启动迟滞现象会更明显。当前仿真模型中超声速扩压段的压力恢复系数σ是固定不变的， 图7（b）是通过在启动和关闭阶段设置不同的压力恢复系数的仿真结果， 可见在喷管进口阀门开启和关闭阶段， 曲线的启动迟滞差异缩小。结果表明超声速压力恢复系数会对仿真舱压结果产生较大影响， 因此在实际应用中需要根据试验结果对不同试验时间段内的压力恢复系数σ修正， 合理取值。需要注意的是， 在图5～6中， 当仿真舱压与自由射流喷管进口总压超过临界压比π2=0.417时， 自由射流喷管出口从亚声速（Ma=0.51）突变为超声速（Ma=2.5）， 即将喷管扩张段内的正激波从出口推了出去， 自由射流喷管达到满流状态， 同时喷管出口的仿真静压也突然下降至最低， 然后喷管出口的仿真静压随着自由射流喷管总压的升高而升高， 最终稳定在可供试验吹风的状态， 表明喷管数学模型较好地模拟了喷管理想状态的启动过程。另外， 注意到在喷管启动过程中， 喷管出口仿真静压与试验静压出现差异， 主要由于试验静压测量位置位于靠近喷管出口内壁面处， 该位置在舱压远高于喷管出口静压时， 极易出现边界层分离， 而当前理想喷管数学模型假设喷管出口为均匀气流， 未能考虑喷管出口的边界层分离的不均匀出口参数， 后续工作需增加喷管模型边界层分离模拟能力。

3 结  论

（1） 仿真舱压与试验舱压的曲线变化规律一致， Simulink模型准确地模拟了整个试验过程中舱压随自由射流喷管进口总压的变化过程， 还准确模拟了自由射流喷管的启动过程、 舱压的启动迟滞现象和舱压与自由射流喷管进口总压的正线性关系等现象， 并且试验状态稳定段的喷管出口仿真静压与试验静压高度吻合， 说明应用Simulink建模方法模拟超声速自由射流试验系统性能具备可行性和工程应用性。

（2） 补气孔面积是舱压调节的关键参数， 试验前需要准确预估补气阀参数设置。压力恢复系数对启动迟滞现象影响较大， 需要根据试验结果对不同试验时间段的压力恢复系数合理修正， 提高仿真准确度。

（3） 目前射流喷管数学模型未包含边界层分离现象， 在喷管启动过程中的喷管出口的仿真值与试验值存在差异， 也没有将引射器数学模型和发动机排气数学模型考虑在内， 在后续工作中， 如高空高马赫数建模分析时， 将会增加这部分内容， 提高仿真准确度。

参考文献：

[1] Dunsworth L C， Reed G J. Ramjet Engine Testing and Simulation Techniques[J]. Journal of Spacecraft and Rockets， 1979， 16（6）：  382-388.

[2] Marren D， Lu F. Advanced Hypersonic Test Facilities[M]. Reston， VA：  AIAA， 2002.

[3] 乐嘉陵. 吸气式高超声速技术研究进展[J]. 推进技术， 2010， 31（6）：  641-649.

Le Jialing. Progress in Air-Breathing Hypersonic Technology[J]. Journal of Propulsion Technology， 2010， 31（6）：  641-649.（in Chinese）

[4] 韩建涛， 孙顺利， 李纲， 等. 固冲发动机进气道半自由射流试验直管扩压器研究[J]. 航空兵器， 2019， 26（4）：  95-98.

Han Jiantao， Sun Shunli， Li Gang， et al. Straight Divergent Tube Research of Semi-Freejet Experiment for Ramjet Inlet[J]. Aero Weaponry， 2019， 26（4）：  95-98.（in Chinese）

[5] Nagaraja K S， Hammond D L， Graetch J E. One-Dimensional Analysis of Compressible Ejector Flows Applicable to V/STOL Aircraft Design[EB/OL].（2012-08-16）[2020-09-02]. AIAA Journal.https：∥doi.org/10.2514/6.1973-1184.

[6] Arun K R， Rajesh G. Flow Transients in Un-Started and Started Modes of Vacuum Ejector Operation[J]. Physics of Fluids， 2016， 28（5）：  056105.

[7] 吴继平. 高增压比多喷管超声速引射器设计理论、 方法与实验研究[D]. 长沙：  国防科学技术大学， 2007.

Wu Jiping. Design Theory， Method and Experimental Investigation of High Compression Ratio Multi-Nozzle Supersonic Ejector[D]. Changsha：  National University of Defense Technology， 2007. （in Chinese）

[8] 陳健. 超-超引射器内部流动过程研究[D]. 长沙：  国防科学技术大学， 2012.

Chen Jian. Researches on the Flow Process of the Supersonic-Supersonic Ejector[D]. Changsha：  National University of Defense Technology， 2012. （in Chinese）

[9] Park G， Kim S， Kwon S. A Starting Procedure of Supersonic Ejector to Minimize Primary Pressure Load[J]. Journal of Propulsion and Power， 2008， 24（3）：  631-635.

[10] Kim S， Kwon S. Starting Pressure and Hysteresis Behavior of an Annular Injection Supersonic Ejector[J]. AIAA Journal， 2008， 46（5）：  1039-1044.

[11] Daniel D. A General Simulation of an Air Ejector Diffuser System[C]∥28th Aerodynamic Measurement Technology， Ground Testing， and Flight Testing Conference， 2012.

[12] 马飞， 王海洲. 基于Matlab/Simulink的气体增压系统建模分析[J]. 导弹与航天运载技术， 2006（3）：  41-47.

Ma Fei， Wang Haizhou. Modeling Analysis of a Gas Pressurized System Based on Matlab/Simulink[J]. Missiles and Space Vehicles， 2006（3）：  41-47.（in Chinese）

[13] Kim S， Kwon S. Experimental Investigation of an Annular Injection Supersonic Ejector[J]. AIAA Journal， 2006， 44（8）：  1905-1908.

[14] 孙顺利， 李纲. 高空模拟引射器启动特性的实验和数值计算研究[J]. 弹箭与制导学报， 2017， 37（4）：  63-67.

Sun Shunli， Li Gang. Experimental and Numerical Research on  the Starting Characteristics of the High Altitude Simulation Ejector[J]. Journal of Projectiles，Rockets，Missiles and Guidance， 2017， 37（4）：  63-67.（in Chinese）

[15] White F M. Fluid Mechanics[M]. New York：  McGraw-Hill， 2003： 599-632.

[16] Anderson J D. Modern Compressible Flow：  With Historical Perspective[M]. New York：  McGraw-Hill， 1990.

[17] 周文祥， 黃金泉， 周人治. 拉瓦尔喷管计算模型的改进及其整机仿真验证[J]. 航空动力学报， 2009， 24（11）：  2601-2606.

Zhou Wenxiang， Huang Jinquan， Zhou Renzhi. Improvement of Laval Nozzle Calculation Model and Simulative Verification in Aero-Engine Performance Calculation[J]. Journal of Aerospace Power， 2009， 24（11）：  2601-2606.（in Chinese）

[18] Pruitt D， Bates L. Starting and Test Rhombus Characteristics of Two-Dimensional Supersonic Free-Jet Nozzle/Generic Supersonic Aircraft Inlet Configurations[C]∥AlAA 4th International Aerospace Planes Conference， 1992.

[19] Van Wie D M， Kwok F T， Walsh R F. Starting Characteristics of Supersonic Inlet[R]. AIAA 1996-2914.

Modeling Analysis of Supersonic Free Jet Test System

Based on Matlab/Simulink

Sun Shunli ， Li Gang， Lu Haiyang

（China Airborne Missile Academy， Luoyang 471009， China）

Abstract：   In order to simulate the dynamic change process of the key index cabin pressure， the key physical process of supersonic free jet test system is modeled based on Matlab/Simulink， and the simulation results are compared with the test results. The curve variation law of the simulated cabin pressure of the model is consistent with that of the test cabin pressure. The error between the simulated cabin pressure and the test cabin pressure in the stable section of the test state is within 1 kPa， and the simulated static pressure at the nozzle outlet and the test static pressure are also less than 1 kPa. At the same time， it also has the ability to simulate the start-up hysteresis phenomenon and the main line relationship between the cabin pressure after startup and the total pressure at the nozzle inlet. The comparative analysis results show that the Simulink modeling method can effectively simulate the dynamic change of cabin pressure of supersonic free jet test system.

Key words：   free jet test;  cabin pressure;  supersonic nozzle;  ejector;  diffuser