Dijkstra标号法在直送式配送运输问题中的应用

刘臣宇 孙伟奇 李卫灵

摘  要：运输路线的选择主要是选择起点到终点的最短路线，路线的选择直接影响到运输成本。最短路线的度量可能是时间最短、距离最短或费用最少等。正确地选择运输路线是运输工作人员的一项重要工作。直送式配送运输是众多运输路线选择问题中的一种，该问题的解法也比较多，但应用Dijkstra标号法来解决复杂的直送式配送运输问题有其独特的优势。

关键词：Dijkstra标号法;直送式配送;方法应用

中图分类号：U116.2    文献标识码：A

Abstract： The choice of transportation route is mainly to choose the shortest route from the start point to the end point. The choice of route directly affects the transportation cost. The measurement of the shortest route may be the shortest time， the shortest distance， or the least cost. Choosing the transportation route correctly is an important task for transportation staff. Direct delivery transportation is one of many transportation route selection problems， and there are many solutions to this problem. However， applying Dijkstra labeling method to solve complex direct delivery transportation problems has its unique advantages.

Key words： Dijkstra labeling method; direct delivery; method application

直送式配送运输是指由一个供应点对一个收货点的专门送货，其货物配送路线的优化就是选择最短的配送路线，以节约时间、费用，提高配送效率。所以直送式配送运输问题，主要是寻找物流网络的最短路问题。对于分离的单个始发点和终点的网络运输路线选择问题，可以有多种解决方法，Dijkstra标号法在解决直送式配送运输问题中具有独特的优势，该方法不仅能够快速找到配送的最短路线，而且还有利于编程计算，最终得到最短距离。

1  Dijkstra标号法

Dijkstra标号法适用于每条弧的赋权数c都大于或等于零的情况，Dijkstra标号法也称为双标号法。所谓双标号法，也就是对图中的点v赋予两个标号l，k，第一个标号l表示从起点v到v的最短路的长度，第二个标号k表示在v至v的最短路上

v前面一个邻点的下标，从而找到起点v到终点v的最短路径及v与v的距离。

对于一个赋权图（其赋权根据具体问题的要求可以是路程的长度，成本的花费等）中指定的两个点v和v找到一条从v到v的路，使得这条路上所有弧的权数总和最小，这条路被称之为v到v的最短路，这条路上所有弧的权数之和被称之为从v到v的距离。如何找到v到v的最短路，可以应用Dijkstra标号法。

Dijkstra标号法求最短路径的算法程序如下：

（1）给起点以标号0，s表示从v到v的距离为0，v为起点。

（2）找出已标号点的集合I，没有标号点的集合J以及弧的集合v，v|v∈I，v∈J，这里这个弧的集合是指所有从已标号点到未标号点的弧的集合。

（3）如果上述弧的集合是空集，则计算结束。如果v已标号l，k，则v到v的距离即为l，从而v到v的最短路径可以从k反向追踪到起点v而得到。如果v未标号，则可以断定不存在从v到v的最短路。

如果上述弧的集合不是空集，则转下一步。

（4）对上述弧的集合中的每一条弧，计算：

s=l+c

在所有的s中，找到其值为最小的弧，不妨设此弧为V，V，则给此弧的终点以双标号scd，c，返回步骤2。

若在第4步骤中，使得sij值为最小的弧有多条，则这些弧的终点既可以任选一个标定，也可以都予以标定，若这些弧中有些弧的终点为同一点，则此点应有多个双标号，以便最后可以找到多条最短路径。

2  方法应用

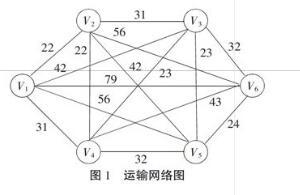
图1为一运输网络，弧线旁的数字为运输距离（单位：千米），试求V到V间的最短路径及其距离。

解：

（1）给起点V标以0，s，表示从V到V的距离为0，V为起点。

（2）这时已标定点的集合I=V，未标定点的集合J=V，V，V，V，V，弧集合v，v|v∈I， v∈J={V，V， V，V， V，V， V，V， V，V}，并有：S=l+c=0+22=22，S=l+c=0+42=42，S=l+c=0

+31=31，S=l+c=0+56=56，S=l+c=0+79=79。

MinS，S，S，S，S=Min22，42，31，56，79=S=22

這样给弧V，V的终点V标以22，1，表示从V到V的距离为22，并且V到V的最短路径中V的前一个点是V。

（3）这时I=V，V，J=V，V，V，V，弧集合v，v|v∈I， v∈J={V，V， V，V， V，V， V，V，V，V， V，V， V，V， V，V}，并有：S=l+c=22+31=53，S=l+c=22+22=44，S=l+c=22+42=66，S=l+c=22+56=78。

MinS，S，S，S，S，S，S，S=Min42，31，56，79，53，44，66，78=S=31

这样给弧V，V的终点V标以31，1，表示从V到V的距离为31，并且V到V的最短路径中V的前一个点是V。

（4）这时I=V，V，V，J=V，V，V，弧集合v，v|v∈I， v∈J={V，V， V，V， V，V，V，V， V，V， V，V，V，V， V，V， V，V}，并有：S=l+c=31+23=54，S=l+c=31+32=63，S=l+c=31+43=74。

MinS，S，S，S，S，S，S，S，S=Min42，56，79，53，66，78，54，63，74=S=42

这样给弧V，V的终点V标以42，1，表示从V到V的距离为42，并且V到V的最短路径中V的前一个点是V。

（5）这时I=V，V，V，V，J=V，V，弧集合v，v|v∈I， v∈J={V，V， V，V， V，V， V，V，V，V， V，V，V，V， V，V}，并有：S=l+c=42+23=65，S=l+c=42+32=74。

MinS，S，S，S，S，S，S，S=Min56，79，66，78，63，74，65，74=S=56

这样给弧V，V的终点V标以56，1，表示从V到V的距离为56，并且V到V的最短路径中V的前一个点是V。

（6）这时I=V，V，V，V，V，J=V，弧集合v，v|v∈I， v∈J=V，V， V，V， V，V， V，V， V，V，并有：S=l5+c=56+24=80。

MinS，S，S，S，S=Min79，78，74，74，80=S=S=74

这样给弧V，V和V，V的终点V标以74，4和74，3，表示从V到V的距离为74，并且V到V的最短路径中V的前一个点是V和V。

（7）这时I=V，V，V，V，V，V，J=Φ，弧集合v，v|v∈I， v∈J=Φ，计算结束。

到此根据终点V的标号可知，从V到V的最短距离是74，最短路径中V的前一个点是V或V，V和V的前一个点是V，即此最短路径为V→VV→V。

3  结  论

在Dijkstra算法中，网络中的每个结点都要进行标号，标号的目的是找出每一点到后面各点的距离和路径，通过比较得到最短路径和最短距离，以此类推，直至终点，因此该算法实际上求出了从起点到网络中各点的最短路径和最短距离。在实际应用中，从起点到终点可能存在多条相同的路径，这时可以根据实际情况任选其中一条路径。

参考文献：

[1] 刘臣宇. 海军航材筹措与供应[M]. 北京：国防工业出版社，2015.

[2] 韓伯棠. 管理运筹学[M]. 2版. 北京：高等教育出版社，2005.