基于特征值屈曲分析的高墩大跨连续刚构桥稳定性研究

郭 森，孟园英

（1. 广东省交通规划设计研究院集团股份有限公司，广东 广州 510507；2. 广州市高速公路有限公司，广东 广州 511400）

0 引言

近年来，因高墩大跨径连续刚构桥梁有受力情况清晰、行车体验良好、施工技术成熟等特点，逐渐被应用到山区高速公路跨越深沟、河流等情况中，并不断朝着高墩、大跨、轻质方向发展[1]。表1 为国内外已建高墩大跨连续刚构桥桥墩型式，其中的空心薄壁墩及双肢薄壁墩因其各自的特点和适用性而被广泛应用于不同地形条件下的连续刚构桥建设中[2]。然而，桥梁的稳定问题却多次出现在薄壁高墩桥梁的施工和运营阶段。不同形式的桥墩直接关系着整个桥梁结构的稳定问题和受力情况，因此对薄壁柔性墩设计和施工中的自体稳定性，T 构最大悬臂状态及通车运营期间，不同阶段结构体系发生改变前后的结构稳定性进行分析极有必要[3]。

表1 国内外已建高墩大跨连续刚构桥采用的桥墩结构型式

陈建伟[1]利用能量法推导了高墩大跨径连续刚构桥中高墩的自身稳定性、悬臂施工稳定系数的理论计算公式，并用有限元程序进行了验证。刘钢城等[4]考虑墩顶为弹性支承，对桥墩压杆计算长度进行了推导。范迎辉[5]对桥墩在墩底、墩顶边界约束条件不同情况下的桥墩临界力及长度系数求解公式进行了分析。张先忠等[6]基于有限元方法，通过欧拉公式将桥梁结构的稳定性与计算长度联系起来进行了分析。本文基于特征值屈曲分析的有限元方法，对高墩大跨刚构桥的稳定性进行分析。

1 桥梁结构稳定性分析理论

1.1 两类稳定问题及界定准则

两端铰支理想弹性直杆受荷载P 作用，处于初始平衡状态，在外界任意存在的微小作用下，能够使其偏离初始的平衡状态，当外界扰动去除后结构能自动回复到初始平衡位置时，则表明结构最初的平衡状态是可靠的。当结构的平衡位置发生变化时，称为结构失稳。当桥梁结构或某一构件一直保持其最初的平衡状态，外界任意微小作用出现时不会使其出现屈曲的最大荷载称为临界荷载，常用Pcr表示。

结构的失稳通常是指结构在外界作用变化到某一特定值时，保持稳定的平衡状态逐渐丧失，扰动略微增大就会使变形急剧增大，最终使结构丧失正常工作水平的情况。

结构稳定问题在桥梁工程中主要表现为2 类：第1 类是以小变形理论为基础的稳定问题，结构屈曲后的荷载- 位移关系如图1 中OABC 段，应归为分支点失稳问题；第2 类稳定问题是以大位移非线性理论为基础的结构极限承载力问题，本质上与结构的强度问题相同，结构屈曲后的荷载- 位移关系如图1 中OBE 段，属于极值点失稳问题。2 类问题的对比见表2。

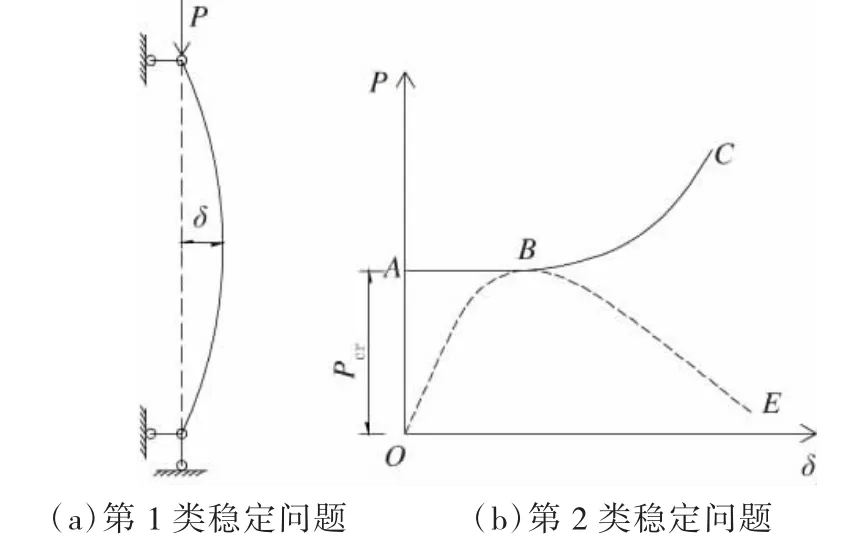
图1 第1、2 类失稳示意图

表2 结构2 类稳定问题对比

桥梁结构实际发生的稳定问题通常属于第2 类失稳。但是由于第1 类稳定问题是特征值问题，一般情况下2 类稳定问题的临界值相差不大，第1 类稳定问题能反映出结构的刚度特征，且其临界荷载又近似地反映第2 类稳定问题的上限，在数学上求解特征值问题比较容易处理，因此对第1 类稳定问题展开研究具有重要的工程意义。

1.2 稳定问题的有限元分析理论

由有限元理论可得结构计算的有限元平衡方程为：

式中：{F}为作用在结构上的荷载力；[K]为弹性刚度矩阵；{δ}为结构在荷载{F}作用 下的位置变化。

弹性刚度矩阵[K]的表达式为：

式中：[KD]是反映杆单元的截面刚度EA 及EI 影响，一般情况下称为单元的弹性刚度矩阵；[KG]与初始轴力F、杆件的几何长度有密切关系，通常称为初始应力刚度矩阵。

根据式（1）、式（2）可以得出结构在荷载作用{F}下的位置变化{δ}。由于[K]与荷载作用相关，若荷载持续增加，则结构位移不断增大；若结构的力与位移不再保持线性关系，则当{F}达到λ{F}时，结构表现为随遇平衡状态，这种情况下，结构已达到临界荷载点。

通常第1 类失稳发生前，结构是满足线性关系的，多数情况下应力与外部作用也呈现线性关系。假设当{F} 增大λ 倍时，杆件几何刚度矩阵也增大λ倍，可得下式：

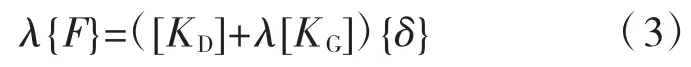
如果λ 足够大，则结构不断呈现随遇平衡状态，即当位移{δ}变为{δ}+{Δδ}时，平衡方程也能够满足，则存在：

按线性代数理论，能够同时满足以上2 式的条件是：

由于{Δδ}有非零解，所以可得：

以上为结构稳定性计算的特征值方程式，稳定问题转化为求方程的最小特征值问题。若方程有n阶，则认为结构会有n 个特征值λ1，λ2，…，λn。但是在实际工程中，有实际应用价值的只有最小的特征值或稳定安全系数[7]。此时的特征值或稳定安全系数即为λcr。

通常情况下，相对于某种确定的荷载而言，结构的稳定性是存在的。但在大跨径桥梁结构中，结构的内力由两部分组成：（1）根据施工过程确定的恒载内力（此部分需按实际施工过程分阶段分析）；（2）后期荷载（如二期恒载、活载、风荷载等）[7]。因此，式（6）可改写成下列形式：

一般情况下，应用结构力学或弹性力学的方法可以解决简单结构的问题；对于复杂结构，若采用解析的分析方法一般无法得出其临界荷载，此时采用有限元的分析方法就能有好的计算结果。

2 桥墩稳定性分析与计算

2.1 依托工程桥梁概况

依托工程桥梁跨越乡镇公路和浔江，江面宽约110 m。桥位区地面标高约228.19～345.15 m，河道与桥梁纵轴线的交角约89°，桥跨布置为75 m+130 m+75 m 预应力混凝土连续刚构桥，主墩采用变截面空心薄壁箱型墩。主桥位于直线段上，桥宽26 m，箱梁标准宽度为12.75 m。依托工程桥型布置图见图2。

图2 依托工程桥型布置图（单位：cm）

2.2 有限元模型的建立

依托工程桥梁为75 m+130 m+75 m(设计线处跨径)预应力混凝土连续刚构桥。根据构件实际尺寸对结构进行计算分析。主桥为主跨130 m 的连续箱梁，5# 主墩墩高为94.76 m，墩高为跨径的1/1.37，6# 主墩墩高为87.71 m，墩高为跨径的1/1.48。

计算考虑主墩及桩基的刚度对上部结构受力的影响。根据地质勘查资料采用土弹簧模拟。结构Midas/Civil 有限元离散图如图3 所示。

图3 结构Mida s /Civil 有限元模型

2.3 施工阶段稳定性分析

查阅现行结构设计规范，在施工和使用阶段，不同规范对结构应具备的第1 类弹性屈曲稳定分析的整体稳定系数要求见表3。

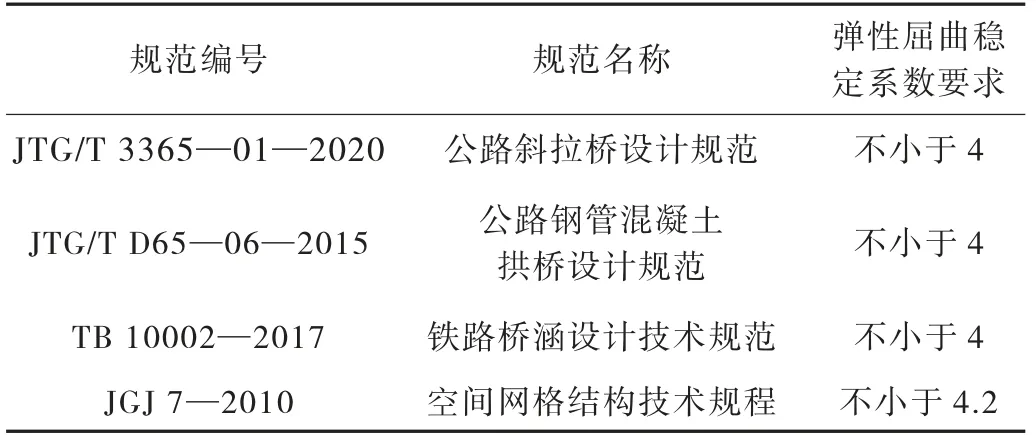
表3 不同规范对第1 类稳定系数的要求

2.3.1 高墩自体稳定性分析

通过桥梁专用计算分析软件Midas/Civil，对桥墩施工期裸墩状态进行自体屈曲分析。屈曲分析时分为2 种荷载类型：第1 类是将一期恒载定义为不变荷载，施工期风荷载定义为可变荷载G+λP，即表3 中的工况3；第2 类为将一期恒载与施工期风荷载定义为可变荷载λ（G+P），即表3 中的工况1、2。通过分析3 种荷载工况来研究风荷载对桥墩稳定性的影响大小。

裸墩状态下稳定性影响因素见表4；裸墩状态下稳定性计算结果见表5。

表4 裸墩状态下稳定性影响因素

表5 裸墩状态下稳定性计算结果

通过分析G+λP 即风荷载作为影响几何刚度矩阵的参考荷载、λ（G+P）即恒载+ 风荷载同时作为影响结构初始应力刚度矩阵的参考荷载，确定这3 种荷载工况对裸墩阶段结构稳定性的影响。

由表5 可见，3 种荷载工况的稳定系数相差较大，在该阶段风荷载不是结构稳定的控制荷载。

2.3.2 施工阶段高墩稳定性影响因素

对最大悬臂状态下的T 构进行施工误差及偶然因素背景下的结构稳定性分析，以便确定影响结构稳定性的关键因素。施工阶段高墩稳定性影响因素见表6。对G+λP、λ（G+P）这2 种荷载类型进行结构稳定性分析，结果见表7、表8。

表6 施工阶段高墩稳定性影响因素

由表7、表8 可知：λ（G+P）类型参考荷载作为结构失稳的控制因素时，G+λP 类型参考荷载对结构稳定的影响可以忽略，该阶段结构1 阶失稳表现为纵桥向失稳；上下行分离结构形式的高墩大跨连续刚构的桥墩横向系梁设置对结构稳定贡献可以忽略，该阶段设置横向连系梁将影响结构的失稳模态，使其不再表现为单墩的失稳。

表7 最大悬臂状态下G+λP 类型稳定性计算结果

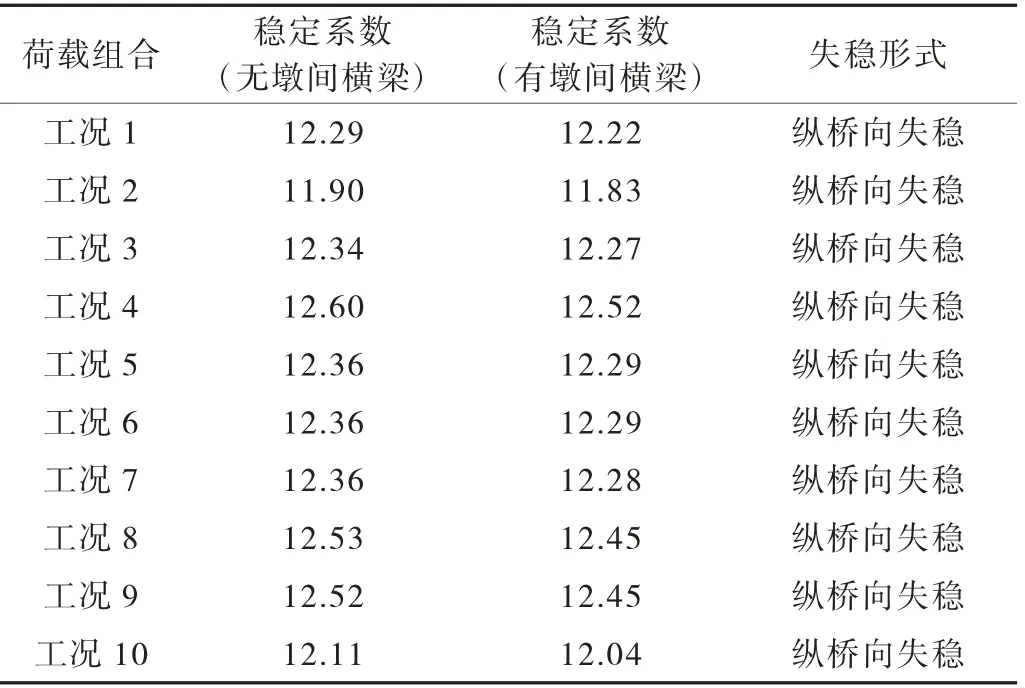
表8 最大悬臂状态下λ（G+P）类型稳定性计算结果

2.4 成桥运营阶段稳定性分析

成桥运营阶段结构体系发生改变时，对结构稳定性产生影响的荷载类型也会发生改变。本阶段将桥梁自重、移动荷载、风荷载作为影响结构稳定的因素（见表9），对成桥阶段结构稳定性进行分析。移动荷载工况分为使墩顶产生最大轴力和最大弯矩的汽车荷载加载工况。

表9 成桥运营阶段高墩稳定性影响因素

成桥状态结构的稳定分析计算结果见表10。本阶段结构体系发生改变而成为超静定结构体系，1 阶弹性屈曲稳定系数远大于4，稳定性不控制设计。

表10 成桥状态下稳定性计算结果

3 结语

（1）裸墩状态下，结构属于静定结构，风荷载作为参考荷载对结构稳定性的影响可以忽略，该阶段稳定性不控制设计。

（2）最大悬臂状态下，结构体系并未发生改变，恒载、偶然荷载和施工误差荷载组合引起的结构稳定性问题风险性较大，在设计和施工阶段对引起结构失稳的因素应引起足够重视。

（3）成桥状态下，结构体系发生改变，属于超静定结构，该阶段对结构稳定性产生影响的各种荷载工况并不控制结构设计。

（4）通过对施工、成桥阶段结构稳定分析可知，稳定系数最小值为11.90，发生在最大悬臂状态下T构状态，是结构稳定分析的控制阶段，因此，在施工阶段应对偶然因素及施工误差进行严格控制。