桁架式拱桥拱肋横桥向风荷载计算方法研究

2021-09-18谭卜豪

城市道桥与防洪 2021年8期

谭卜豪，王雷，王同

（广东省交通规划设计研究院股份有限公司，广东广州 510507）

0 引言

随着科学技术的发展，我国及世界桥梁建设得到了快速发展。特别是我国西部大开发以及一带一路建设，西部地区将建设更多的交通设施。但是我国西部地区多为山区峡谷地形，因此需要修建许多跨越峡谷的桥梁。拱桥因其不需要在峡谷中落墩，充分利用地形地势的特点，满足了经济性并且与环境和谐统一，从而成为跨越山区峡谷的首选桥型。但是山区峡谷地形复杂，昼夜温差较大，往往风速较大。并且根据张志田、谭卜豪等人对深切峡谷风场研究中指出，山区峡谷地形对顺峡谷方向（横桥向）风荷载有加速效果[2]。因此桥址处风速会进一步增加。因此，在桥梁设计时，会更加关心风的作用。但是由于拱桥结构形式相比于斜拉桥与悬索桥，结构刚度较大，风振响应不明显，因此实验研究拱桥抗风特性的研究较少。并且目前规范[1]中，主要针对梁桥、斜拉桥、悬索桥做了相对细致的要求。但是对拱桥的相关验算与规定还比较少。

但是，从静风荷载角度考虑，由于拱桥横桥向风荷载使得拱桥面外受力，因此不能发挥拱桥将弯矩转化为轴力的优势，对于拱桥受力不利。因此常常成为大跨度拱桥设计的控制因素。由此，深入研究拱肋阻力系数，精确计算拱肋横向风荷载，对于拱桥设计有非常重要的意义。

1 工程概况

本研究以某大跨度中承式钢管混凝土拱桥为研究对象，见图1，全桥跨径组合为6×2 5m 小箱梁+388 m 中承式钢管混凝土拱桥+5×25 m 小箱梁。主拱肋采用四肢桁式钢管混凝土结构，净跨径360 m，计算矢跨比为1/4，拱轴系数为1.55。双片拱肋中距31 m，肋宽4 m，拱顶桁高6.5 ，拱脚桁高12 m。桥宽32.2 m，吊杆间距为15.2 m。主拱主管钢材采用Q390qD，其余钢材采用Q355D。双片拱肋之间采用“Δ+I”形式横撑。主梁采用格子钢梁叠合22 cm 混凝土的组合结构。

图1 某钢管混凝土拱桥立面图

由于所在区域基本风速很大，需要对主桥进行详的抗风验算。

2 规范计算局限性

在进行风荷载计算时，根据规范[1]四肢桁架式钢管混凝土拱肋，按照桁架主梁式计算风荷载，由于其没有桥面板，气动特性将与桁架式主梁存在较大差异。并且规范主要针对桁架式主梁，而主梁由于通行需要桁架中心间距较宽，普遍间距比（两桁架中心/迎风桁架高度）普遍偏大。规范给出的桁架遮挡系数η 与间距比关系中，间距比取值范围在1～6 之间。但是桁架式拱肋由其受力特点，一般间距比取值在0.25～1 之间。由此，不同间距比的拱肋其桁架遮挡系数取值按照规范基本不变，计算结果是否适用于桁架？

按照《公路桥梁抗风设计规范》[1]5.4.2 拱肋风荷载可以按照杆件的阻力系数取值，单当多肢构成且间距小于5 倍单肢拱肋宽度，根据规范需通过风洞试验及虚拟风洞确定阻力系数Cd。由此，是否可以找到可靠的拱肋阻力系数计算方法，成为解决拱桥抗风问题的主要问题。

3 阻力系数计算方法与参数分析

按照桁架形式来计算四肢圆柱桁架型拱肋单位长度横向风荷载Fg计算公式见式（1）：

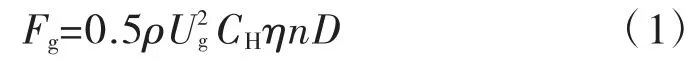
式中：CH为单片桁架阻力系数；η 为拱肋遮挡系数；n为拱肋片数；D 为拱肋高度。根据规范[1]可知CH值与实面积比与间距比有关。

3.1 间距比b 与阻力系数的关系

但是规范上没有规矩单层桥面板和双层桥面板对阻力系数做进一步区分，由此说明阻力系数对是否存在桥面板情况较为不敏感。但是由于桁架主梁受车道数影响，往往呈现扁平形式，间距比在1～6之间。所以，规范上给出了间距比1～6 与阻力系数的关系表格。由于拱肋间距比一般在0.25～1 之间，为了使其更好的满足拱肋形式，需要进一步细分0～1 之间间距比与阻力关系，根据特性分析考虑到b 值接近无穷时，阻力系数渐近线为1，而当b=0 时，阻力系数为0.5，再根据规范已有数据估计间距比在0.25～0.75 之间的阻力系数如果依旧按照1 对应的阻力系数，计算结果可能偏于保守。

3.2 实面积比a 值与阻力系数的关系

根据统计多个四圆柱桁架型拱肋尺寸，其实面积比一般在0.3～0.7 之间，根据《抗风规范》5.3.2 圆柱形构件，且dUd＞6 杆件，横向力系数CH=0.8，但是在相同间距比情况下随着实面积比的增加折减系数将大幅下降，当实面积比在0.6～0.7 是，如果按照0.5 实面积比对应的阻力系数取值，取值将偏于保守。

3.3 通过单个构件方法计算阻力系数

抗风规范中有专门对拱肋规定，如果是单根拱肋，可以按照桥墩截面计算阻力系数，如果是多根构件且间距大于5 倍半径可以按照单根构件计算。四圆管桁架考虑受风面构件，按照单肢杆件分别计算得到的拱肋单位长度阻力Fg公式见式（2）：

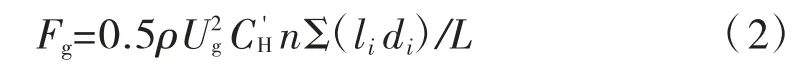
式中：li为各杆件长度；di为各杆件直径；C'H为修正后杆件平均阻力系数。

根据统计四圆柱型桁架肢间距比（单肢宽度/ 两支净间距）一般在1～1.5 之间，远小于规范要求的5。故四圆柱型桁架拱肋不能仅仅按照规范计算。按照单肢拱肋确定的拱肋阻力系数为C'H=0.6，由于仅仅计算了迎风面上杆件的面积的风阻，忽略了风撑、横联对圆柱绕流的影响，按照完全光滑的圆形杆件作为阻力系数往往偏于危险，由此可以按照粗糙的或有凸起的圆形截面进行模拟，故保守估计阻力系数C'H可以取值1.2。

3.4 单个构件阻力系数与整体计算阻力系数换算关系

由于风洞试验一般是按照节段模型测量整体模型的阻力系数即CHηn，而CFD 模拟的更多为二维多圆柱绕流，各圆管断面平均阻力系数为C'H。需要进行适当的转换方便对两者计算结果进行对比。同样可以分析两种计算方法，取值的关系见式（3）～式（6）。

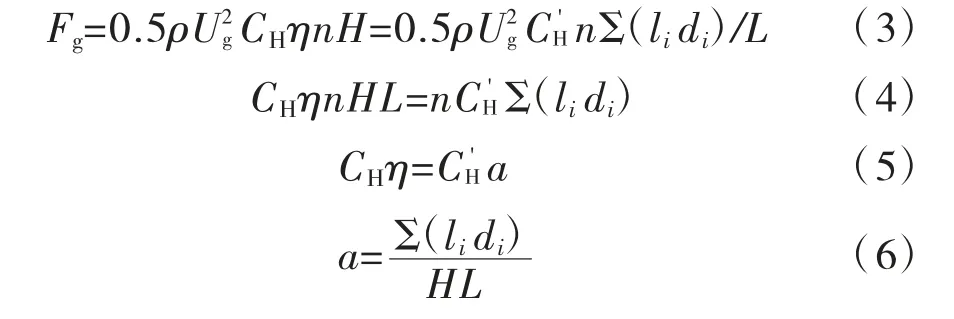
由公式可知a 为实面积比。即可以推出整体的阻力系数与平均每个杆件的阻力系数存在的差别为实面积比。

3.5 雷诺数修正

由于圆柱断面绕流形式与雷诺数大小十分敏感[3]，在进行风洞试验或缩尺的CFD 模拟时，阻力系数都需要对其进行雷诺数修正。经典圆柱绕流阻力系数Cd值计算公式见式（7），由公式可知: 实际桁架结构雷诺数一般在106～107之间，处于跨临界与超临界范围，而缩尺比模型一般在103～104处于跨临界范围。试验测量的阻力系数与雷诺数关系如图2 所示：故不进行雷诺数修正直接测得的阻力系数会相对偏大。

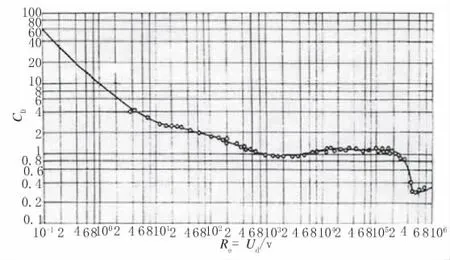
图2 阻力系数与雷诺数关系

4 实验与CFD 计算阻力系数结果

4.1 平南三桥

根据广西大学沈川、谢开仲等的研究内容可知[4]总体布置：计算跨径560 m，净跨径548 m，主桥长575 m。失跨比1/4，拱轴系数1.5。节段具体尺寸见表1，其中主要参数意义见图3。

表1 平南三桥节段尺寸

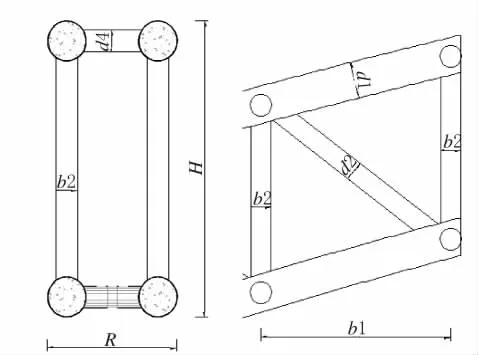
图3 节段尺寸

通过二维CFD 数值模拟计算截面阻力系数计算结果如下图所示：

雷诺数修正后计算结果见表2。

表2 CFD 模拟的杆件阻力系数

由于修正后阻力系数变化趋势，随拱肋的高度增加而减小。其界面高度从17 m 变化到8.5 m 阻力系数从0.96 变化为1.08 变化幅度不到10%；故可以认为对拱肋高度变化较为不敏感，可以按照最小高度计算出的进行保守计算。

4.2 茅草街大桥

根据同济大学于洪刚、葛耀君等人研究内容可知[5]其总体布置见图4，主跨368 m；失跨比1/5，拱轴系数1.543，节段具体尺寸见表3。

图4 茅草街大桥桥型布置图

表3 茅草街大桥节段尺寸

拱肋通过1∶20 缩尺比模型风洞试验测得的气动三分力系数见表4，其中分段见图5。

表4 试验测得节段整体阻力系数

图5 茅草街大桥拱肋模型分段示意图

4.3 浙江三门口北门大桥

根据葛耀君等研究结果可知[5]分段形式：跨径270 m，失跨比1/5；拱轴系数m=1.543；拱高5.3 m，提篮拱桥，节段尺寸见表5，其中节段划分及断面形式见图6。

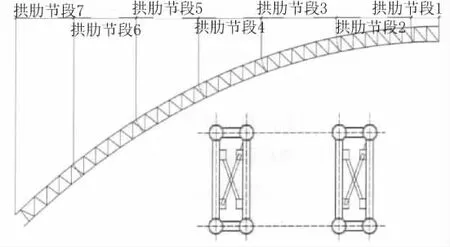
图6 北门大桥拱肋模型分段示意图

表5 北门大桥节段尺寸

根据节段模型试验测量的三分力系数需要考虑雷诺数修正结果见表6。

表6 试验测得节段整体阻力系数

4.4 风洞试验

根据吴欣荣等人的研究[6]，其制作了3 个节段试验验算四圆管桁架式拱肋三分力系数，模型参数见表7。

表7 风洞实验模型节段尺寸

其模型主要变量为模型宽度，可以验证随宽度变化，阻力系数的变化情况，其模型结果为整体三分力系数CHηn 见表8。

表8 试验测得节段整体阻力系数CHηn

由试验结果可知，桁架宽度越大阻力系数呈上升趋势。

5 参数分析与实际桥梁应用

5.1 某特大桥参数

某拱桥参数见表9。

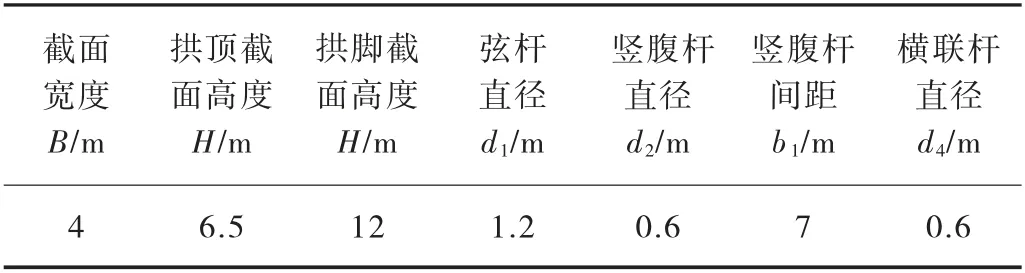
表9 某拱桥节段尺寸

5.2 阻力系数值参数敏感性分析

对于四圆柱钢管混凝土桁架截面，估目前认为阻力系数的含参数方程为：CH=f（a，b），根据式（4）～式（6）将阻力系数相互转化计算结果见表10、表11。

表10 各桥实面积比与间距比

表11 各桥阻力系数

由表11 可知：（1）除了茅草街大桥，其他桥梁拱肋杆件横向力系数C'H均小于规范圆形截面阻力系数1.2。（2）而根据桁架计算方法，计算出的阻力系数CHηn 换算为杆件C'H值，在拱顶处小于圆形截面阻力系数C'H，而在拱脚普遍大于圆形截面C'H，经过分析主要原因可能是，随着间距比b 值的变化，阻力系数应该发生对应变化，但是规范中间距比在0～1 范围内，根据3.1 节推算，当间距比b 越来与小时，值接近与0.5；比实际取值0.8 小，故规范取值过于保守，所以拱脚阻力系数想比与实测杆件计算结果偏大。（3）通过实验数据可知，变截面高度的拱肋，拱脚和拱顶的杆件阻力系数C'H没有很大变化，按照圆形杆件的计算方法，更贴近实验结果。

综上，如果桥梁没有进行风洞试验，拱肋阻力系数取值可以按照圆柱杆件形式，阻力系数取值为1.2进行计算较为合理。