基于卡尔曼滤波的遥测数据野值剔除方法

2021-09-18朱红运苗岩松庞建国

航天返回与遥感 2021年4期

朱红运苗岩松庞建国

（太原卫星发射中心，太原 030000）

0 引言

在航空、航天等试验中，由于受飞行器姿态、传感器性能、天线方向及飞行器振动等因素影响，遥测数据中有时会存在异常跳变的值，这种由测量设备或传输过程产生的严重偏离正常值的数据称为野值[1-5]。野值的出现将严重影响对遥测信号特征的分析，因此，剔除野值是分析遥测信号特征的一个重要前期步骤[6-8]。

目前，常用的野值处理方法主要有三种[9-10]：一是在分析数据统计特性基础上，通过设置合理的阈值对野值进行判别和剔除，主要有罗曼诺夫斯基准则、狄克松准则及莱特准则等；二是通过提取并分析数据特征对野值进行判别和剔除，主要有小波变换方法、信号特征提取方法等；三是求取并分析数据的估计值与原始值差的统计特性来进行判别。第一种方法未充分利用原始测量数据中包含的信息，误差较大；第二种方法算法复杂、计算量大；第三种方法大多基于滤波为最优情况，而对非最优滤波情况下的野值检测及处理能力有限。

卡尔曼滤波具有滤波效果好、实时性强等优点，已在工程实践中得到了广泛应用[11-14]。鉴于此，为有效剔除遥测数据中野值并降低背景噪声干扰，本文提出了一种基于卡尔曼滤波的遥测数据野值剔除方法，该方法在采用卡尔曼算法对遥测数据滤波时，通过引入判别因子降低滤波系统误差的影响，并利用判别因子对野值进行修正；最后通过仿真实验对该方法的有效性进行了验证，并将其应用于遥测信号野值剔除实例。

1 野值对卡尔曼滤波结果的影响

卡尔曼滤波算法是一种递归的估计算法，仅根据前一时刻状态值和最近一次观测数据就可估计当前值[15-16]。采用卡尔曼滤波时，首先用系统状态方程和观测方程两个基本的方程式来描述需要测量的系统，系统状态方程和观测方程分别为[17-18]：

式中X(k)、U(k)分别为k时刻系统状态和状态控制量；A、B为系统的参数；Z(k)为k时刻观测值；H为测量系统参数；W(k)、V(k)分别为符合高斯分布的过程噪声和测量噪声。

预测过程可表示为：

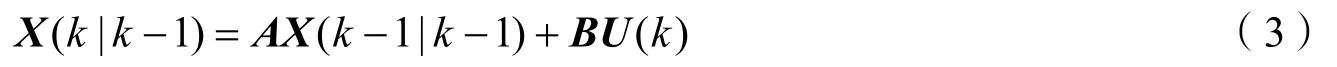
式中X(k|k-1)为k-1时刻对k时刻的预测值。

系统误差协方差为

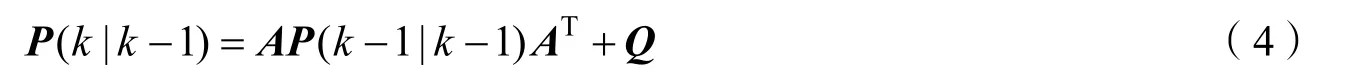
式中P(k|k-1)为k-1时刻对k时刻系统误差协方差的预测；Q为W(k)的协方差。

此时，k时刻最优估计值可表示为

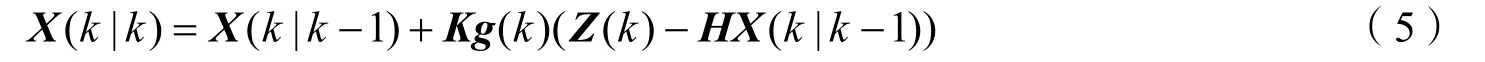
式中X(k|k)为k时刻最优估计值；Kg(k)为卡尔曼增益，其表达式为

式中R为V(k)的协方差。

系统误差协方差最优值为

式中I为单位矩阵。

至此完成一次完整的卡尔曼滤波。卡尔曼滤波过程是通过不断迭代进行的，每得到一个新的观测值就进行一次迭代。由式（5）可知，在迭代过程中，使用观测值Z(k)对预测值进行了修正，式中Z(k)-HX(k|k-1)称为新息[19]，其主要反映了系统误差和测量误差的和，可用e(k)表示，即：

当滤波系统为最优时，e(k)为服从高斯分布的白噪声。

当观测值为野值时，由式（5）可知，野值对新息的影响将被放大为原来的Kg(k)倍引入到系统中，新息的特性会受野值的干扰，严重时最终会导致滤波发散，因此，在卡尔曼滤波过程中必须对野值进行剔除。

2 野值剔除

2.1 莱特准则判别法

莱特准则是常用的野值判别方法[20-21]，其基本原理为：当数值服从高斯分布时，数值位于其三倍方差[-3δ,3]δ区间内的概率不小于99.7%，即处于此区间外的数值不超过0.3%，莱特准则判别方法也称为3δ方法。在卡尔曼滤波过程中，当出现野值时，野值对应时刻新息会出现突变，因此，落于新息序列三倍方差之外的新息可认为是由野值产生的，由此可实现对野值的判别。

在实际遥测数据采集及处理过程中，由于事先很难准确确定过程噪声和测量噪声，滤波系统有时为次优的滤波系统，此时，新息序列往往也不是希望的服从高斯分布的白噪声，因此当滤波系统非最优时，直接采用莱特准则判别野值会存在一定的误差。此外，卡尔曼滤波过程中，目前常用的野值剔除方法是直接使用预测值代替野值，由于该方法未使用观测值对预测值修正，因而影响滤波精度。为此，本文通过引入表征新息序列统计特性的判别因子，提高基于莱特准则的野值判别准确度及卡尔曼滤波精度。

2.2 野值判别与剔除

由上述分析可知，当卡尔曼滤波系统非最优时，即使无野值存在，新息序列总体上也不符合高斯分布，此时，k时刻新息可表示为

式中ek1为k时刻由滤波系统非最优原因而引入的系统误差；ek2为服从高斯分布的测量误差；则k时刻前新息序列的均值Sk可表示为

式中i为1,2,···,k的整数。

当无野值存在时，由于ek2服从高斯分布，均值Sk主要反映了由滤波系统引入的误差。当信号中出现野值时，测量误差ek2会出现突变，此时其均值也会发生跳变，为提取野值引起的突变特征，引入判别因子kμ，其表达式为

由上述分析可知，当信号中不存在野值时，可认为判别因子μk近似为0，当出现野值时，可利用μk=0逆向推导出野值点处观测值，而后使用该观测值对卡尔曼滤波过程中预测值进行修正，即可消除野值干扰。

综上，本文提出的基于卡尔曼滤波的遥测数据野值剔除方法具体步骤为：步骤 1，对遥测信号进行卡尔曼滤波，求取k时刻前的新息序列；步骤2，分别计算k及k-1时刻前新息序列的均值，而后求得k时刻判别因子μk；步骤3，采用莱特准则分析判别因子μk特征，识别野值；步骤4，利用μk=0逆向推导出野值点处观测值，而后对卡尔曼滤波过程中预测值进行修正，完成一次完整卡尔曼滤波。

3 实验验证

3.1 仿真分析

为消除野值对卡尔曼滤波结果的影响，文献[22]根据马哈拉诺比斯距离定义提出了一种修正卡尔曼滤波方法，该方法能够有效地识别野值，并消除野值对滤波的不利影响。鉴于此，为检验所提方法的性能，采用文献[22]方法和本文方法分别对含野值且含有一定噪声的仿真信号进行处理，原始含野值信号及两种方法处理结果如图1所示。原始信号信噪比为10dB，野值分别位于信号第300、500、700及1000个采样点处。

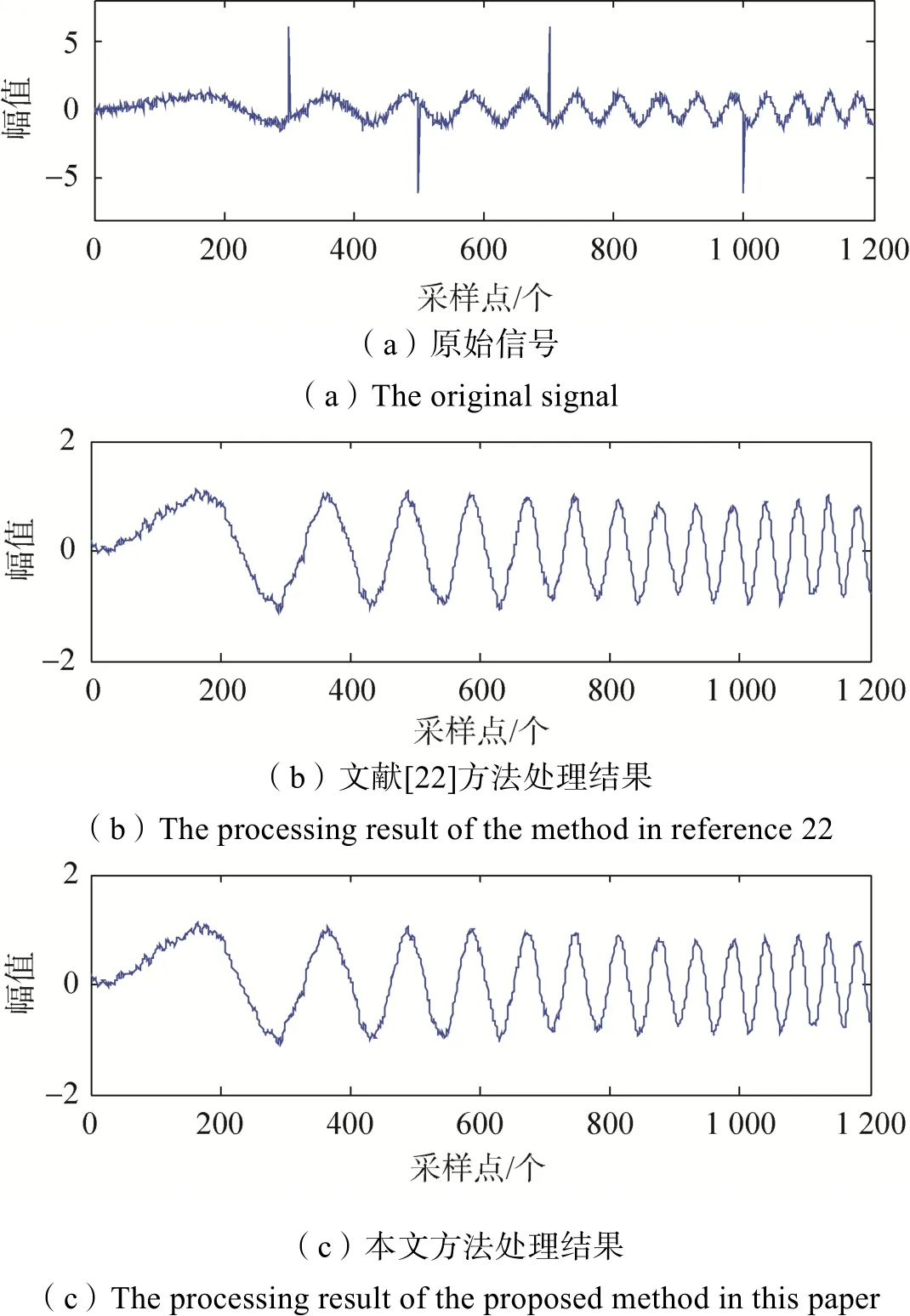
图1 不同方法的处理结果Fig.1 The processing results of different methods

由图1可以看出，文献[22]方法及本文所提方法均能有效剔除野值，且对背景噪声有较好的抑制作用，在对信号处理过程中，野值点处对应原始信号真实值分别为-0.82、0.76、-0.89、-0.48，采用卡尔曼方法得到的预测值分别为-0.71、0.65、-0.99、-0.37；采用本文方法对预测值进行修正，而后得到最终滤波结果分别为-0.78、0.77、-0.93、-0.43；文献[22]方法得到最终滤波结果分别为-0.76、0.74、-0.94、-0.41，可知本文所提出的方法得到的结果与真实值相差更小。为进一步定量分析二者性能，采用信噪比对二者处理结果进行评判，文献[22]方法及本文方法处理后信号信噪比分别为 13.52dB、13.95dB，可知本文方法在剔除野值的同时，对噪声的抑制作用更强，性能更好。这是因为在采用本文方法对信号处理时，引入的判别因子能够降低滤波系统误差的影响，且利用该判别因子推导野值点处观测值，并采用该观测值对野值进行修正，可在剔除野值的同时进一步提高卡尔曼滤波精度，因而该方法性能更好。

为进一步检验本文方法的鲁棒性，将上述原始含野值信号信噪比分别设置为 10dB、8dB、6dB，而后分别采用上述两种方法对不同信噪比条件下原始含野值信号进行处理，处理前后信号的信噪比如表1所示。

表1 不同方法处理前后信号的信噪比Tab.1 Signal to noise ration of signals before and after processing by different methods单位：dB

由表1可知，当原始信号信噪比不同时，两种方法都能降低噪声干扰，提高信号的信噪比，但对于同一个含噪信号，由于本文方法通过引入判别因子降低了系统误差的影响，且对野值进行了修正，在剔除野值的同时提高了卡尔曼滤波精度，因而该方法降噪后信号的信噪比更大，随着噪声强度增强，该方法仍具有较好的降噪性能。

3.2 算法应用

某电压遥测信号数据曲线如图2所示，可以看出，由于受测量设备或传输过程影响，整个电压遥测数据曲线包含一定的噪声且包含多个野值点，在对电压分析时，特别是对突变时刻电压分析时，噪声和野值的存在很可能会导致误判。

图2 原始电压遥测信号数据曲线Fig.2 The data curve of original voltage telemetry signal

为降低噪声干扰，并有效剔除野值，采用本文所提方法对该遥测数据进行降噪及剔除野值处理，结果如图3所示。

通过对比图2、图3可知，本文提出的基于卡尔曼滤波的遥测数据野值剔除方法在降低背景噪声干扰的同时，可有效剔除遥测数据中的野值，提高遥测信号的可识别性。由此表明，文中引入的判别因子能够有效反映野值特征，通过采用莱特准备对判别因子分析，可准确识别遥测信号中的野值位置，且利用判别因子推导的野值点处观测值包含了较多的有用信息，利用该观测值对卡尔曼滤波过程中预测值进行修正，能够有效消除野值干扰，可知本文提出的基于卡尔曼滤波的遥测数据野值剔除方法是一种有效可行的遥测数据野值剔除方法。