基于数值模拟的填方路基沉降规律研究

李浩霖，李 斌，柯凯艳

（云南建设投资控股集团有限公司国际工程部，云南昆明650000）

随着经济的发展，公路的建设也开始慢慢向偏远地区转移，伴随而来的是施工工况复杂性的增加，因此我们需要有针对性的分析讨论路基变形的外部情况，更好地为施工服务。

对于填方路基，赵炼等[1]运用器材冲击压路机，完成了石子含量在60%～70%的填方路基施工中的研究。刘海明等[2]建立了PMIGM(1,1)预测模型，成功地将模型运用于填方路基实践中，验证了该模拟可以完成对预测模型精度的提高。冯学钢[3]结合工程实例，给出了路基沉降的防治方案。Liu[4]根据填方路基监测数据，提出了一种基于粒子群优化（PSO）和马尔可夫链的填方路基监测模型PSOMGVM。Jia[5]为了研究重力作用和车辆荷载作用下填方路基的施工后沉降，对兰—永高速公路进行了现场监测。上述学者均未考虑填土高度、路基坡高比、填料和压实度等影响因素对填方路基变形的影响。所以本文从填方路基入手，选用MIDAS软件，建立填方路基截面数值模拟，模拟了在填土高度、路基坡高比、填料和压实度不同情况下的路基沉降情况。

1 模型建立

为研究填方路基变形的影响因素，本文拟选取公路等级为二级，路基顶面宽12m，地基由30m厚粘土层和50m厚基岩构成，考虑边界效应，取水平长度60m。在现场工作时，路基压实度按照规范选取。土体的物理力学参数见表1。

表1 土体的物理力学参数表

此次模型中的土体采用摩尔—库仑进行模拟，在分析时由于填方路基可以归纳为轴对称平面应变问题，依照对称性原则完成对模型的假设：①土的渗流速率恒定可以忽略时间的影响；②土为弹塑体；③土体中水的流动遵从达西定律；④土是连续的，且土体均匀[6]。

采用MIDAS GTS有限元软件建立公路模型，并完成对模型的网格划分，由于地基在变形中位移量较小，因此划分较为稀疏；路基在变形中的位移量相对来说较大，因此在划分网格的时候较为密集，在不影响计算精度的同时，加快计算进程。网格划分效果图见图1，在对边界施加约束时，考虑实际情况，对路基底部采用完全约束；对地基横向施加约束，竖向不施加约束。

图1 填方路基网格划分效果图

2 结果分析

2.1 不同高度的填方路基沉降分析

采用摩尔—库伦模型完成对不同高度填方路基的模拟，收集并整理在2m、4m、6m、8m、10m的填方高度下的位移变化量，得出如表2所示沉降结果，并完成填土高度与位移变化图（图3），得出相关结论。

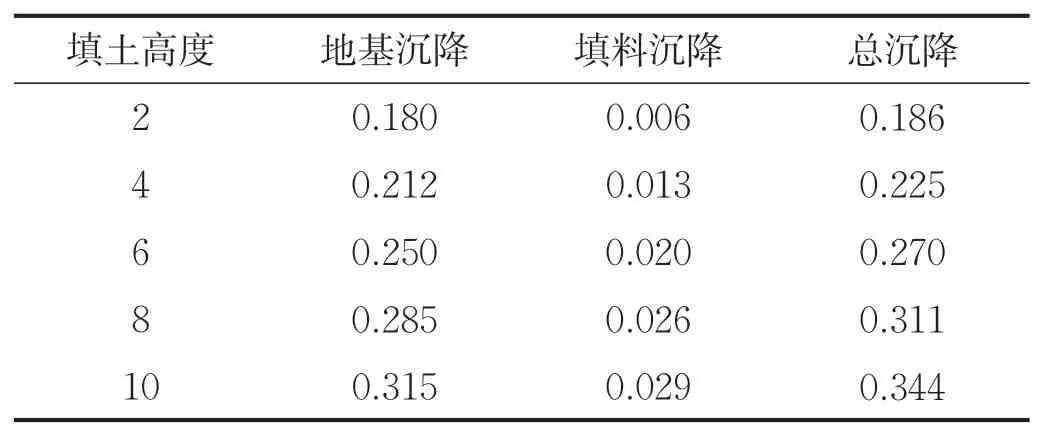
表2 不同填土高度的沉降结果（单位：m）

由图2分析可得：①随着填土高度的增加，地基路基均产生沉降，地基沉降较为明显，从2m时沉降0.18m到10m时的0.328m，变化幅度为0.148m。由图可以清楚看到，总沉降随着填方高度增加而呈线性增大的趋势。②从图像我们可以看出在增加填土高度的同时，对地基破坏很大，地基沉降占到总沉降的一半还要多，所以在进行填方路基施工时，要避免过高的堆填，减少填方路基的施工；实在避免不了的情况下，我们要对地基进行强度改造，确保工程的安全施工。

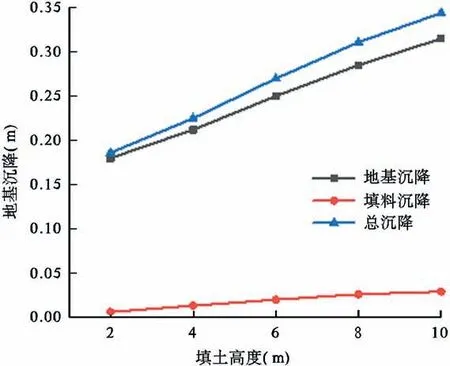
图2 不同填土高度下沉降图

2.2 不同坡高比的填方路基沉降分析

在实际工程中，坡高比的变化也会导致地基沉降的变化，基于此，开展关于不同的坡高比模型试验，在对边界施加约束时，考虑实际情况，对路基底部采用完全约束；对地基水平施加约束，竖直方向不施加约束。分别考虑在坡高比为1∶1、1∶1.25、1∶5、1∶1.75、1∶2情况下路基沉降。

在表3沉降结果基础上，为了清晰地看到沉降的变化情况，完成了如图3的沉降图。

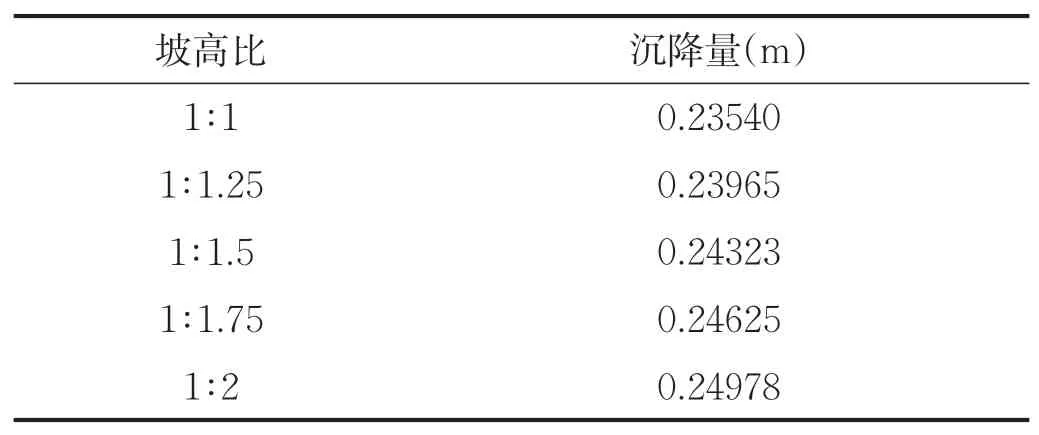
表3 路基在不同坡高比下的沉降结果

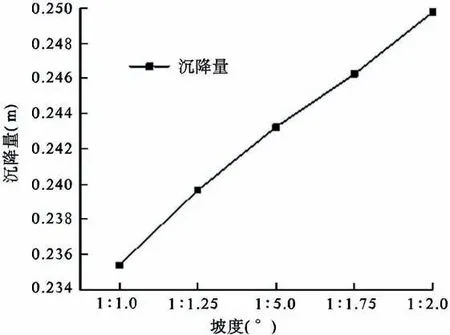
图3 不同坡高比下沉降效果图

由图3分析可得：在坡高比为1∶1时，路基沉降量为0.235m，当坡高比为1∶2时，沉降量为0.25m，沉降量随着坡高比的增加，而呈近似线性增大；在坡高比从1∶1到1∶2的过程中，沉降变化幅度0.014m，表明变化幅度对路基沉降影响不是很大，但是在实际施工过程中还是要避免坡高比过大情况的发生，防止滑坡等灾害的发生。

2.3 不同填方材料的路基沉降分析

随着公路的飞速发展，我国对公路的认识也随之增强，公路施工也渐渐摆脱了地域的束缚，这些建立在施工技术的增长，对填方材料认识的加强。选则恰当的填方材料，才能更好地确保公路的安全实施。规范规定只有达到一定强度，且本身能被压缩到制定密度的，并能形成稳定填方的才适合被用于填方工程[7]。基于此，本文收集并整理了相关规范，收集了路基施工中常用的填方材料，材料性质见表4。

表4 填方材料物理性质

开展关于不同的材料模型试验，在对边界施加约束时，考虑实际情况，对路基底部采用完全约束；对地基水平施加约束，竖直方向不施加约束。考虑不同填土导致地基沉降变形情况见表5。

在表5沉降结果基础上，为了清晰地看到沉降的变化情况，完成了如图4的沉降图。

表5 不同填方材料导致地基沉降

由图4分析可得：①路基总变形量是由路基变形量和地基变形量之和，填料自身的容重是导致地基变形的主要影响条件。根据不同材料下沉降效果图可知，新型材料聚苯乙烯泡沫作为容重最低的材料，在这些材料中变形是最小，变形量为0.16m。根据沉降效果图，可以看出，在填方路基中要最大程度降低地基变形量最有效办法就是采用容重最小的材料，即最大程度降低材料重量。②在实际工程中，由于聚苯乙烯泡沫和磷石膏成本较高，所以一般不会作为填方路基的填筑材料，但在地质条件较差的地区，可以优先选择聚苯乙烯泡沫和磷石膏作为路基填筑材料；粉煤灰作为工业废渣自身堆放会造成一系列问题的产生，比如占用土地资源，污染堆放地的环境的问题。因此实际应用中，更多地选用粉煤。这样免去土地的占用，保护了环境，更做到了废物利用一举多得。

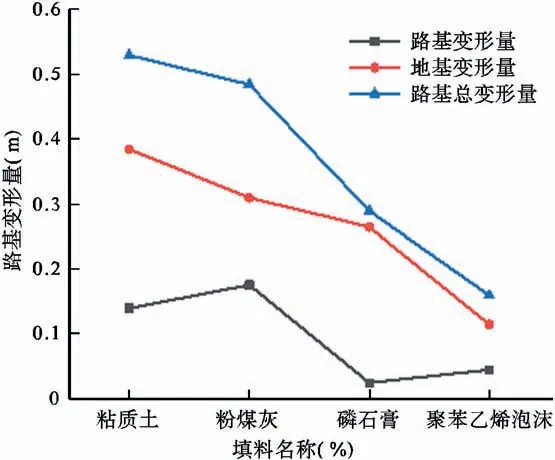
图4 不同材料下沉降效果图

2.4 压实度的路基沉降分析

压实度是材料本身的一个属性，在路基施工中作为质量检测以及材料选取的重要指标。压实度代表了材料属性的好坏，压实度较大的材料，自身整体性较好。本研究遵照规范，选取压实度90%以上的材料，旨在寻求压实度对路基沉降的影响效果。

开展关于不同的材料模型试验，在对边界施加约束时，考虑实际情况，对路基底部采用完全约束；对地基水平施加约束，竖直方向不施加约束。根据现场经验可知，因此，本文选取低液限粘土在90%、92%、94%、96%、98%情况下对比研究地基沉降的具体情况。所得结果见表6。

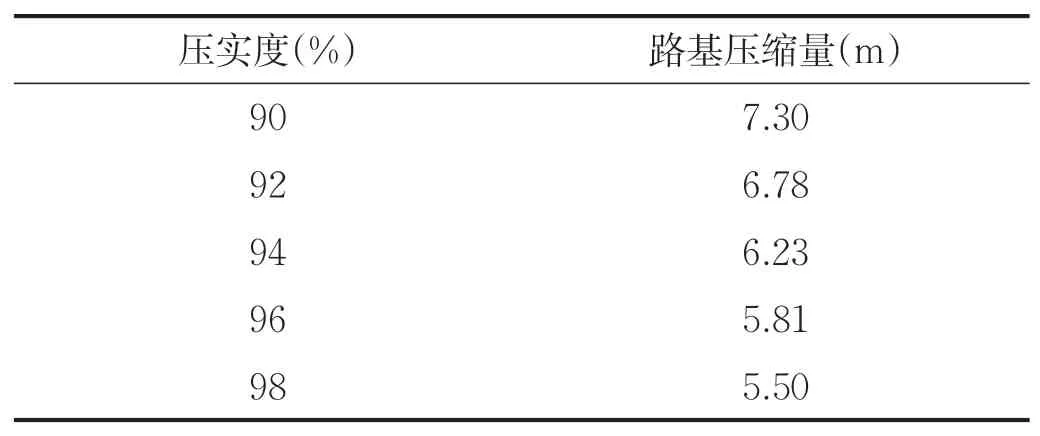
表6 不同压实度导致地基沉降

由图5分析可得：对于同种材料，随着压实度的增加路基压缩量在明显降低，在规范规定的情况下，尽可能增加压实度，能保证工程的安全性。可以从图中明显看出压实度从90%至98%变形下降幅度为25%。这往往意味着成本的增加。在实际工程中，结合实际情况选择压实度，不仅能提高工程质量，而且成本还能在预期范围内。

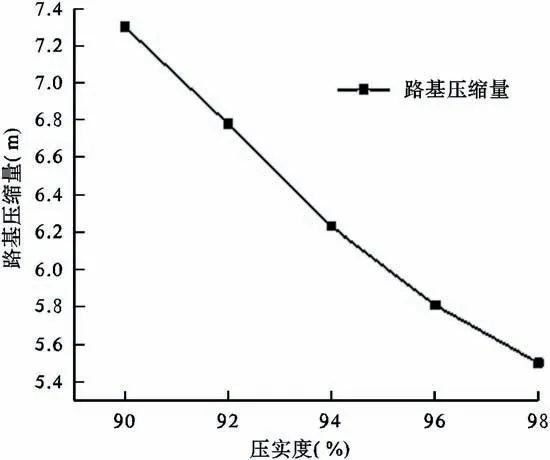
图5 同种材料不同压实度下沉降效果图

3 结论

本文运用MIDAS GTS模拟了填方路基在填筑高度、路基坡高比、材料、压实度的情况下路基沉降情况。

（1）在填方路基中，随着填筑高度的增加，路基沉降呈线性增加趋势，在工程应用中，由于滑坡及自重影响，尽量降低填筑高度。

（2）在填方路基中，坡高比的增大，导致沉降量随着增加，在坡高比从1∶1到1∶2的过程中，沉降变化幅度为0.014m，沉降变化幅度不是很大，但在实际工程中还是要降低坡高比，防止滑坡等灾害的发生。

（3）在填方路基中，新型材料聚苯乙烯泡沫作为容重最低的材料，变形量是最小的，变形量为0.16m。在填方路基中要最大程度降低地基变形量最有效办法就是采用容重最小的材料，即最大程度降低材料重量，在实际工程中，考虑经济效益，结合施工需要达到的要求，合理选择施工材料。

（4）对于同种材料，压实度的增加导致变形在明显降低，在实际应用中，选择恰当的压实度，在确保工程质量的同时，成本还能在预期范围内。