The Comparison of Three Different Solution Decomposition Schemes for Poisson-Boltzmann Models
2021-09-17LiJiaoGuoRongHuJialuanYingJinyong
Li Jiao Guo Rong Hu Jialuan Ying Jinyong
(1.School of Mathematics and Statistics,Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering,Changsha University of Science and Technology,Changsha 410114,China;2.School of Mathematics and Statistics,HNP-LAMA,Central South University,Changsha 410083,China)
Abstract To deal with the singularity in Poisson-Boltzmann models caused by fixed charge distribution in biomolecules,several decomposition schemes have been proposed in literatures.In this paper,three commonly-used decomposition schemes,the two-term decomposition scheme,the three-term decomposition only in biomolecular domain,and the three-term decomposition in the whole domain,for Poisson-Boltzmann models are reviewed and compared.Numerical tests on a Born ball model with analytical solution show the performance of each scheme.
Key words Poisson-Boltzmann model Two-term decomposition scheme Three-term decomposition scheme Singularity Biomolecule
1 Introduction
A commonly-used electrostatics model,called the Poisson-Boltzmann equation (PBE),in biomolecular simulations with a symmetric 1:1 electrolyte usually has the following form:
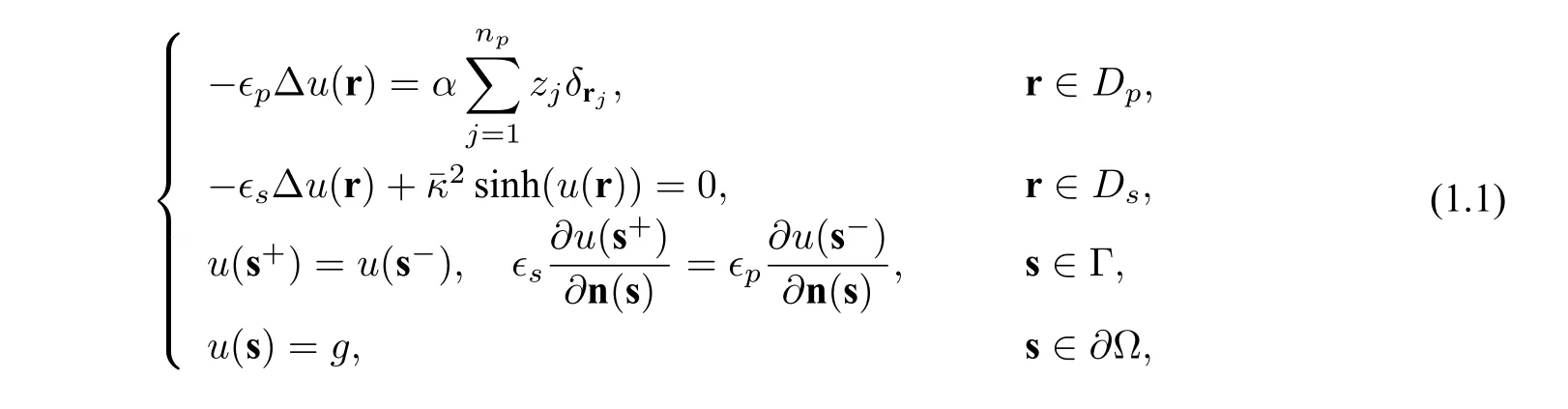
where Ω is a given sufficiently large connected and convex domain satisfying Ω=Dp ∪Ds ∪Γ with the protein domainDpbeing surrounded by the solventDsand Γ being the interface betweenDpandDs(Γ is assumed to be of classC2to guarantee the existence and uniqueness of the solution analytically,see[3]for example),ϵpandϵsare dielectric constants inDpandDs,respectively(we setϵp=2.0 andϵs=80.0 in this paper),uis the dimensionless electrostatic potential,gis a given function,∂Ω denotes the boundary of Ω,δrjis the Dirac delta distribution at point rj,n(s)is the unit outward normal vector ofDp,andαandare defined by
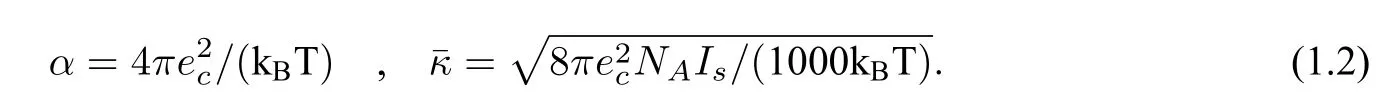
Hereecis the elementary charge,kBis the Boltzmann constant,Tis the absolute temperature,Isis the ionic strength,andNAis the Avogadro constant,which estimates the number of ions per mole as 6.02214129×1023.In electrostatic units(esu),ecandkBare estimated by
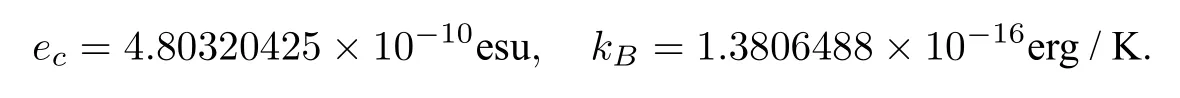
In biomolecular calculation,the domain Ω is measured in angstroms(Å).Thus,the length unit should be converted from centimeter(cm)to angstrom(1cm=108Å).ForT=298.15KandIs=0.1 mole per liter,which are often used in numerical tests,αand2can be found to have the following values

The PBE given in(1.1)is difficult to analyze and solve numerically due to its singularity caused by the fixed charge distribution in biomolecules,the coefficients’jump on interface between biomolecule domain and solvent domain,and its strong nonlinearity caused by the exponential functions.To overcome these issues in analyzing and solving PB models,there are several decomposition schemes in literatures[1-11].We introduce three commonly-used decomposition schemes and show their performances in this paper.
Based on the performances of these three schemes,the choice of the decomposition depends on the applications since different requirements are posed in different applications.For example,protein docking and protein binding are highly correlated with the electrostatic potential at the surface of the biomolecule,while some bimolecular activities are occurred through the solvent and thus the electrostatic potential outside the biomolecule is expected.
The remaining sections of this paper are organized as follows:In Section 2,we briefly review the definitions and features of these three commonly-used decomposition schemes.Section 3 introduces the program package for solving PBE based on these three decompositions.Numerical results for these schemes on a Born ball model are reported in Section 4.Section 5 gives the conclusions.
2 Review of three decomposition schemes
In this section,we briefly review the definitions and features of three decomposition schemes.
2.1 Two-term Scheme(Scheme 1)
A two-term scheme was proposed and analyzed in [1],which is motivated by the physical interpretation of the solution of PBE and decomposes the solution into two components,based on the distinct solvent domainDsand the molecular domainDpin the model.This scheme can be described in the following way:For a solutionuof(1.1),it can be decomposed as

whereuRis a solution of the following equation

andGis given by


This natural decomposition splits the PBE into a singular functionGhaving a regularized well-posed PBE(2.2)ofuRand a simple closed form expression given in(2.3).Numerically,the singular componentGgiven by (2.3) is obtained before the solution of (2.2).The weak form solution of (2.5) is given by:finding

such that∀v ∈
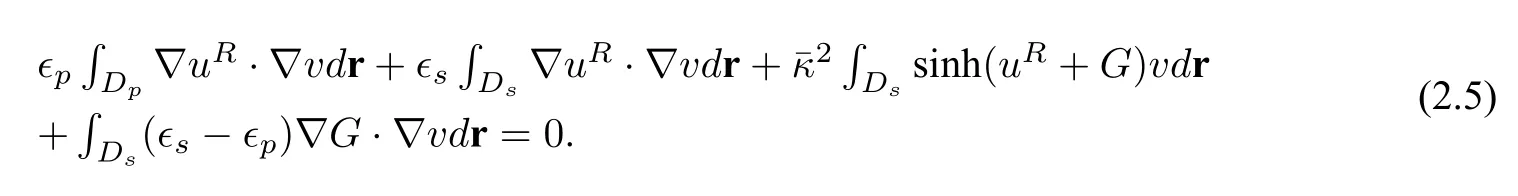
2.2 Three-term decomposition in biomolecule domain scheme(Scheme 2)
A second decomposition scheme proposed in[2]is often used[12,15].This decomposition splits the solutionuof PBE(1.1)into three parts in the protein domain only,described as below:

whereuhis a solution of the harmonic equation

the singular componentGis the restriction of the solution of(2.3)toDp,and the regular componentursatisfies the equation
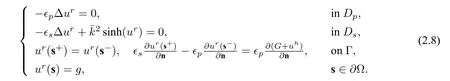
In this decomposition,Gis easy to get,anduhcan be obtained by seeking a solution of the weak form:findinguh ∈H1(Dp)andu=−Gon Γ,such that
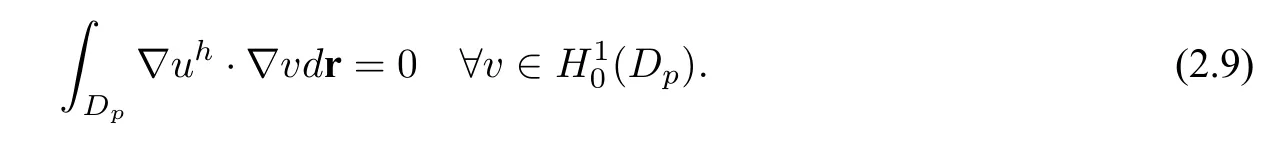
Therefore,Ganduhare known before the solution of nonlinear equation(2.8)forur.And the weak form solution of(2.8)is given by:finding
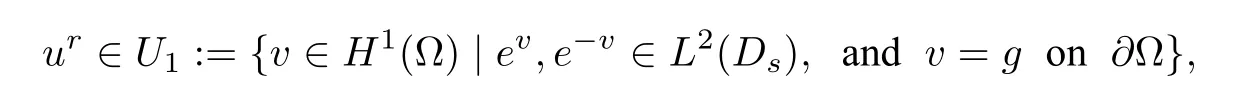
such that
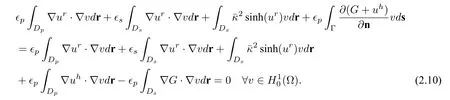
2.3 Three-term decomposition in the whole domain scheme(Scheme 3)
Another solution decomposition proposed in[3]naturally splits the NPBE solutionuinto three parts,G,Ψ,and,within both the solute domainDpand the solvent domainDs,according to electrostatic contributions from the biomolecular charges,the boundary and interface conditions,and the ionic solvent charges,respectively.This decomposition has the form

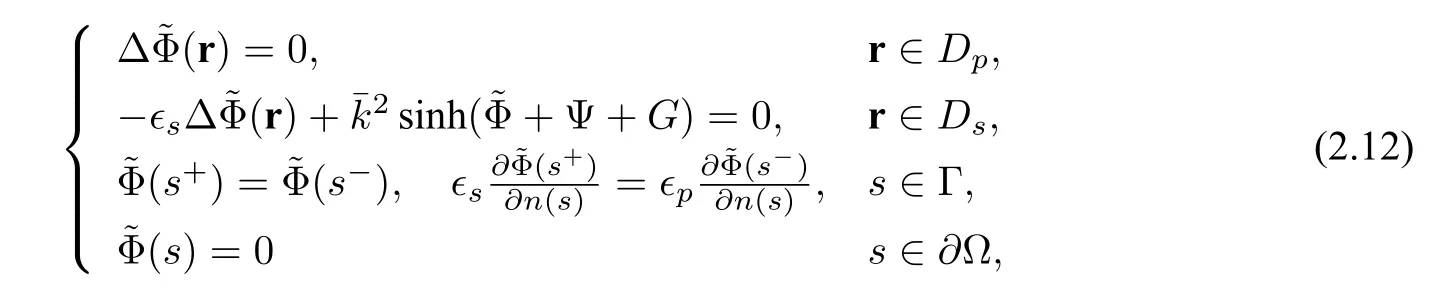
Ψ satisfies the equation

andGis given by(2.3).
In this decomposition,the jump interface condition is collected in term Ψ,which is a solution of a linear problem(2.13)and is easy to obtain,whose weak form is given as follows:finding Ψ∈H1(Ω)and Ψ=g −Gon∂Ω,such that

Before solving the nonlinear problem(2.12),Gand Ψ are available,andis a weak form:finding

such that

2.4 Features of these three schemes
The features of these three schemes are introduced in this section.
Features of the two-term decomposition scheme(Scheme 1)are described as below:
• Scheme 1 has significant importance in theory and makes possible the development of a complete solution and approximate theory for the PBE.
• Since the nonlinear term of the PBE is given in the form sinh(uR+G),when solved by a Newton type method,it may cause an overflow problem when an initial guess ofuRis not well selected,e.g.settinguR=0 will result in thatGbecomes a dominated part at some mesh points,this will cause a huge value of sinh.
• We notice that the term

for Scheme 1 induced by the interface condition,stays in the weak form of nonlinear problem(2.2).This causes more cost to solve the nonlinear problem and may lead to failure in finding solution for the nonlinear problem when the total charge inDpis large.
• Moreover,numerical tests in[12]showed that small relative error of regular partuRwould cause large perturbation in the full potentialudue to different magnitude dielectric constants inDpandDs.Hence,numerical algorithm based on this decomposition may fail sometimes.
Features of the three-term decomposition in bimolecular domain scheme(Scheme 2)are described as below:
• The Poisson boundary value problem ofuhoverDpmay be difficult to solve due to a complicated shape ofDp,which may not be convex and may have a nonsmooth boundary.Thus,its solution may not be inH2(Dp),causing the difficulties in its numerical solution.
• For equation(2.7)ofuhin Scheme 2,its domainDpmay be irregular and nonconvex,which may cause difficulties to solve equation(2.7).
• The nonlinear equation (2.8) ofurhas singularity on the interface Γ caused by the jump discontinuous interface condition,which induces the term

stays in the weak form of nonlinear problem(2.8).This may cause more cost to solve the nonlinear problem and may lead to failure in finding solution for the nonlinear problems when the total charge inDpis large.
• Moreover,it is more complicated in numerical implementation for components in (2.6) since two different function spaces are required by using finite element method.
• The undetermined part of the nonlinear term sinh(u)isufor Scheme 1 andfor Scheme 2.
• Since there is no decomposition ofuinDs,errors in numerical solutions ofurare not amplified inuinDs.
Features of the three-term decomposition in the whole domain scheme(Scheme 3)are described as below:
• The treatment of the flux jump discontinuity on the interface and the non-homogeneous boundary condition is moved to the linear problem(2.13)of Ψ.As a result,the nonlinear problem(2.12)ofhas the continuous interface conditions and a homogeneous boundary condition.Hence,it can be more efficiently solved than the nonlinear problems from the other two schemes.
• Since the part Ψ+Ggives the potential of a protein in water,the nonlinear problem(2.12)ofcan be solved by a Newton-type method using zero as an initial guess without instability problem.
3 Program package for solving PBE based on these three decompositions
A finite element program package in Python based on our previous package[13]is produced in this paper.All involved boundary value problems are approximated by a finite element method,and then solved by the linear iterative solver GMRES with the ILU preconditioner from the PETSc library.
In all numerical tests,we set the relative and absolute tolerances of GMRES as 10−10,and use values ofαandgiven in(1.3).All the tests are made on one 2.8 GHz Intel Core i7 processor of a MacBook Pro with 4GB memory.
At first,we describe the algorithm to solve the PBE based on these three decompositions as below:
Algorithm 1
Step 1 Generate a mesh.
Step 2Gby(2.3)and∇Gby(2.4).
Step 3 Obtain a solutionuhof(2.9)and a solution Ψ of(2.14).
Step 4 Call a nonlinear solver to find the solutionsuR,ur,andfor(2.5),(2.10),and(2.15),respectively.
Step 5 Obtain the solutionufor PBE(1.1)by decomposition(2.1),(2.6),or(2.11).
To generate a mesh,the following steps are used in this paper:at first,we use DOLFIN [14] to generate a triangulation on the sphere of two spheres with radiuses 1 and 5,respectively; then Tetgen(http://tetgen.org) is used to generate the Delaunay tetrahedralizations based on the input triangulation generated in DOLFIN.To verify the stability of these schemes,an original meshM,the mesh refined onMdenoted byM1,and the mesh refined onM1 denoted byM2 are used.To avoid sharp increase of the number of vertices,we take the bisection refinement strategy instead of uniformly refinement to refine the meshes.
In these three solution decomposition schemes for the PBE,the componentsGand Ψ are easy to obtain.And foruh,there are two ways to solve the equation(2.7)in DOLFIN,provided that we only have a mesh on the whole domain Ω.Let the mesh beMand we present the two approaches in the following:
(1) Based on the meshM,we calculate the solution of(2.7)by extending the current protein domainsDpto the whole domain Ω and then applying the boundary condition on the interface Γ and on∂Ω,that is,(2.7)is equivalent to the problem:finding

such that
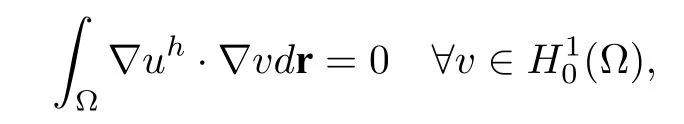
then restrict the solutionuhtoDpafter obtaining the solutionuhin the whole domain Ω.
(2) Another approach to solve equation(2.7)is to extract the sub-mesh containing the vertices on interface Γ and inside the protein domainDpfromM,then follow the routine procedure in DOLFIN to obtain the solution.
These two ways lead to similar results,except the small difference caused by solving two different linear equations.
We next focus on seeking for solutionsuR,ur,andto nonlinear problems(2.2),(2.8)and(2.12)by solving(2.5),(2.10)and(2.15),respectively.A modified Newton-type method from[16]is employed to find the solutions of these variational problems.And the following minimization problem is considered:

wherev∗is the minimizer as the solution of the variational problem considered.We need to find the corresponding functionalJ(v)for each variational problem.The modified Newton method is described as follows.

Step 4 Decide a steplengthλk:set steplengthλk=1,if

go to step 5,otherwise,decideλkby a line search algorithm to satisfy(3.3)and go to the next step.Step:=k+1.Go to Step 2.
4 Numerical tests for the three schemes
To compare these three schemes numerically,we use the following nonlinear Born ball model,i.e.a point charge lies in the origin of a unit ball,whose analytical solution is available:
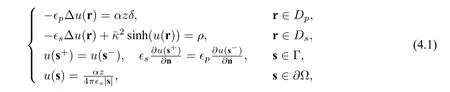
where Ω = {r : |r| < Rs},Dp= {r : |r| < Rp},Ds= {r : Rp< |r| < Rs},Γ = {r : |r| = Rp},z is a charge number,ρ=,and δ is the Dirac delta distribution at the origin. The analytical solution of this Born ball model is given by

To do tests on this model,we need to modify the equations(2.2),(2.8)and(2.12)by adding the termρin(4.1)to the right hand side of their second equations.
For Scheme 1,we solve the following linear problem ofuRto obtain a good initial guess for the Newton method:

and then,define the following functional for minimization problem(3.1):

whose first and second derivatives are found as


We first do numerical tests for these three decomposition schemes on the nonlinear Born ball model(4.1)without truncation on the terms sinh(ϕ) and cosh(ϕ),in other words,skipping step 2 in the modified Newton method.In these numerical tests,we have three meshes,that is,an original meshMwith 3763 vertices,a meshM1 with 19523 vertices obtained from refiningM,and a meshM2 with 72247 vertices obtained from refiningM1.
Numerical results for these three schemes with two different initial guesses,the solution of the corresponding linear problem and zero,for solving nonlinear partuRare presented in Table 1.Herez=1,and its relative errorwith respect to the analytical solution,and the number of iterations are reported.
From Table 1,we can see that Scheme 1 is sensitive to initial guesses,when zero is selected as its initial guess,it blows up,while Schemes 2 and 3 are stable for different initial guesses,except that one more iteration is needed for initial guess zero.We note that Scheme 2 has the highest solution accuracy on coarse meshesMandM1,and the solution accuracy of all Schemes are increased as the increase of mesh points.Note that on the finest meshM2,the solution accuracy of these three schemes are very close.
Since these schemes would encounter the blow-up problem for largez,the modified Newton method is used,that is,with truncation on the terms sinh(ϕ) and cosh(ϕ).Numerical results for these three decomposition schemes solved by the modified Newton method are presented in Table 2.
From Table 2,we can easily calculate how much time each step takes for these three schemes,e.g.,each step of Scheme 1 takes 0.16,0.71,and 3.08 on meshesM,M1,andM2,respectively,thecorresponding data for Scheme 2 are 0.19,0.80,and 3.24,and for Scheme 3 are 0.13,0.62,and 2.64,which is as predicted theoretically,each step of Schemes 1 and 2 is more costed than that of Scheme 3,due to the extra terms in(2.5)and(2.10)induced by the interface conditions.

Table 1 Performance of the three schemes for the nonlinear Born ball model(4.1)with different initial guesses in Newton method without truncation.Here Rp=1,Rs=5,and an original mesh M (3763),a refined-once mesh M1(19523),and a refined-twice mesh M2(72247)are used by a linear finite element method.

Table 2 Comparison of the three schemes for the nonlinear Born ball model(4.1)with linear solution as initial guess in modified Newton method(bound=300).Here Rp=1 and Rs=5,the original mesh M (3763),the refined-once mesh M1(19523),and the refined-twice mesh M2(72247)are used by a linear finite element method.
Furthermore,we compare the three-term schemes 2 and 3 on different domains.Relative errors of Schemes 2 and 3 for the nonlinear Born ball model (4.1) in molecular domainDp,interface Γ,solvent domainDs,and the whole domain Ω are reported in Table 3.And the distributions of relative errors of these two schemes along the radius|r|are reported in Figure 1.
From Table 3 and Figure 1,we can see that Scheme 2 has smaller relative error in solvent domainDsthan Scheme 3,and Scheme 3 performs better on interface Γ and protein domainDp.
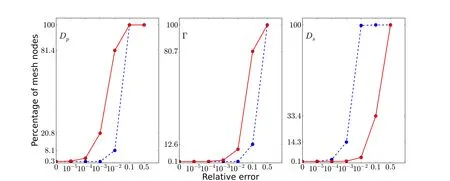
Figure 1 Percentage distributions of the solution relative errors of the finite element solutions of PBE in Dp,Γ,and Ds,respectively,based on Scheme 2(in blue dashed line)and Scheme 3(in red line)for the nonlinear Born ball model(4.1)with z=1,Rp=1,and Rs=5 on M1.

Table 3 Relative errors of Schemes 2 and 3 for the nonlinear Born ball model(4.1)in molecular domain Dp,interface Γ,solvent domain Ds,and the whole domain Ω.Here z=1,Rp=1,Rs=5,and an original mesh M (3763),a refined-once mesh M1(19523),and a refined-twice mesh M2(72247)are used by a linear finite element method.
5 Conclusions
In this paper,three commonly-used decomposition schemes for Poisson-Boltzmann models,the two-term decomposition scheme(Scheme 1),the three-term decomposition in biomolecular domain only
(Scheme 2),and the three-term decomposition in the whole domain (Scheme 3),are reviewed and compared.Numerical tests for these three decomposition schemes on the nonlinear Born ball model(4.1) with analytical solution show that Scheme 2 and Scheme 3 are more stable for different initial guesses than Scheme 1.And Scheme 2 has the highest solution accuracy on coarse meshes.What’s more,Scheme 2 performs better in solvent domainDswhile Scheme 3 performs better on interface Γ and protein domainDp.Hence,we can choose suitable decomposition schemes based on different requirements in applications.For examples,protein docking and protein binding are highly correlated with the electrostatic potential at the surface of the biomolecule,while some bimolecular activities are occurred through the solvent and thus the electrostatic potential outside the biomolecule is expected.
杂志排行
数学理论与应用的其它文章
- 一类具有非线性扰动的新冠肺炎SIRC 随机模型研究
- 环境噪声驱动下的个体群集动力学研究
- Further Discussion for Generalized Normal Sectors in Class II
- Distance Integral Graphs Generated by Strong Sum and Strong Product
- Well-posedness and Dispersive Limit Behavior for the Solutions to a Generalized Hyperelastic-rod Wave Equation
- An Improved Image Fusion Method Based on a Wavelet Transform
