典型地层直径对无支护圆形基坑稳定性影响分析

金 星

（中铁十六局集团有限公司 北京 100018）

1 引言

近年来，诸多学者对基坑稳定性进行了深入研究。冯忠居等［1］为定量分析圆排式异型深基坑支护的侧向变形特性与抗隆起稳定性，利用数值仿真软件对矩形深基坑及圆排式异型深基坑进行对比研究，结果表明圆排式异型深基坑相比于矩形深基坑具有足够的安全性与稳定性。郑军峰［2］以厦门地铁2号线育秀东路站基坑工程为背景，采用数值模拟方法，分析了不同地层参数对基坑支护体系稳定性的影响规律。闫国良［3］以某基坑工程为依托，基于有限元分析方法，分析了基坑支护结构的受力变形规律，并进一步研究了桩间距对基坑稳定性的影响。张明聚［4］等通过推导圆形基坑抗隆起稳定性安全系数计算公式，并采用三维轴对称滑动圆弧法对圆形基坑抗隆起稳定性进行验算，结果表明该方法相比于其他平面算法更为合理。王洪新［5］等推导出圆形基坑的抗倾覆稳定安全系数计算公式，并通过对比相应参考文献中的模型试验及数值模拟结果，验证了该公式的合理性。王卫东等［6］基于非线性有限元提出了轴对称条件下基坑坑底抗隆起稳定分析的强度折减方法，指出采用平面轴对称有限元的强度折减法分析得到的坑底抗隆起稳定系数较平面应变有限元强度折减分析得到的稳定系数高得多。王炳龙等［7］通过对连续墙不同入土深度时某地铁风井圆形基坑的设计方案进行离心模型试验，得出直径小于30 m的圆形基坑入土系数的合理取值范围，并总结出圆形基坑位移规律。然而，对于无支护情况下直径对圆形基坑的稳定性影响鲜有文献报道。

本文采用数值模拟的方法，对典型地层无支护情况下直径对圆形基坑稳定性影响进行分析，并将数值模拟结果与相应规范进行比较［8－10］，判断圆形基坑的稳定性，以期为相关实际工程提供借鉴。

2 工程概述及模型构建

2.1 工程概况

本研究分别选取广州、南昌、上海地区典型地层，通过数值模拟的方法，在无支护情况下，随基坑直径不断变化，对相应地层进行分析，并与基坑相关规范进行比较，以判断基坑的安全性。由于上海地区土层分布多为深厚软土型，而广州、南昌地区土层分布多为上软下硬型，因此，以上海淤泥土、粉质黏土作为典型地层，以广州或南昌风化岩层及基岩层作为典型地层进行分析。

通过调研典型地层基坑工程可知，近五年多以深基坑为主，且开挖深度大多小于30 m。工程施工中，基坑深度超过5 m为深基坑，超过20 m为超深基坑［9］。为了保证分析过程中，仅有直径作为自变量对圆形基坑无支护情况下的稳定性产生影响，以深度5 m作为淤泥层、粉质黏土层的开挖深度；考虑到风化岩及基岩的物理力学特性，分别以深度20 m、25 m、30 m作为风化岩层、基岩层的开挖深度。

2.2 数值模拟

本研究采用Midas GTS有限元软件，对典型地层在无支护情况下，基坑直径对基坑稳定性的影响进行分析。根据相关工程经验及基坑开挖深度影响，且考虑到直径过大引起的边界效应以及风化岩及基岩的物理力学特性，将模型尺寸定为400×400×90 m（X、Y、Z），不考虑地下水及其他因素的扰动作用。有限元模型及土层参数如图1、表1所示。

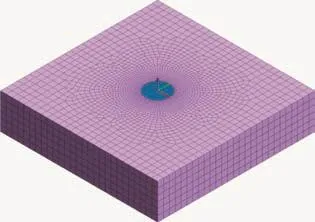
图1 有限元模型

表1 土层物理力学参数

三维模型采用摩尔－库伦本构，对模型各侧边界进行法向约束，顶部为自由面，底面为固定节点的三项约束（X、Y、Z）。考虑计算的简便性，基坑开挖区域设置网格较密集，向四周逐渐稀疏。具体工况：（1）初始地应力平衡并位移清零；（2）开挖至基坑底部。

3 典型地层稳定性分析

3.1 稳定性判定依据

随着数值分析手段的进步和计算机性能的提高，采用强度折减是有限元分析稳定性的有效方法，即在理想弹塑性有限元计算中将岩土体抗剪强度参数逐渐降低直到其达到破坏状态为止。其中，分析稳定性的一个关键问题是失稳的判据问题。

三维圆形基坑开挖从俯视角度可看作为隧道的掘进过程，从而基坑开挖后的稳定性判别可采用隧道掌子面稳定性的判别依据。因此，本研究主要采用位移突变或有效塑性应变从坑底至坑顶贯通作为失稳破坏的标志［11］。

3.2 数值结果分析

（1）淤泥层稳定性分析

为了直观表现基坑失稳时，有效塑形应变区域的变化情况，同一挖深、不同直径下的基坑塑性区域云图如图2所示。由图2可知，随基坑直径的增大，有效塑性应变区域逐渐增大；直径2 m时，基坑开挖区域有效塑性应变已贯穿至基坑顶部。根据失稳依据可知，淤泥层基坑在挖深5 m时，发生失稳现象的临界直径约为2 m。

图2 不同直径下淤泥层基坑塑性应变云图

（2）粉质黏土层稳定性分析

图3为粉质黏土层基坑在同一挖深、不同直径下的基坑水平位移曲线。可以看出，随着基坑直径的增加，基坑水平位移逐渐增大。当直径小于5 m时，基坑位移增加速率较为平缓；当直径大于5 m后，基坑位移增加速率较快。根据失稳依据可知，粉质黏土层基坑在挖深为5 m时，发生失稳现象的临界直径约为5 m。

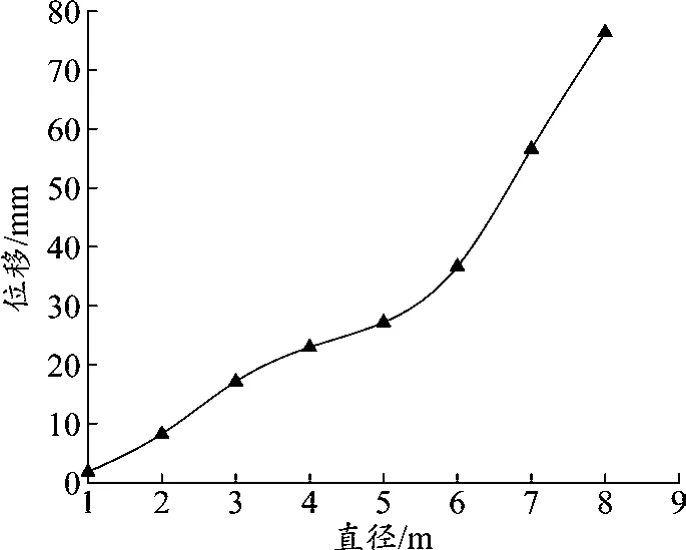
图3 不同直径下粉质黏土层基坑水平位移曲线

（3）风化岩层稳定性分析

图4为风化岩层基坑挖深为20 m、25 m、30 m时，基坑水平位移随直径变化曲线。可以看出，随基坑直径的增加，基坑水平位移均逐渐增大。挖深20 m时，当直径小于60 m，基坑位移增长速率较为平缓；当直径大于60 m，基坑位移增长速率较快。挖深25 m时，当直径小于30 m，基坑位移增长速率较为平缓；当直径大于30 m，基坑位移增长速率较快。挖深30 m时，当直径小于20 m，基坑位移增长速率较为平缓；当直径大于20 m，基坑位移增长速率较快。根据失稳依据可知，挖深20 m、25 m、30 m时，风化岩层基坑失稳的临界直径分别约为60 m、30 m、20 m。

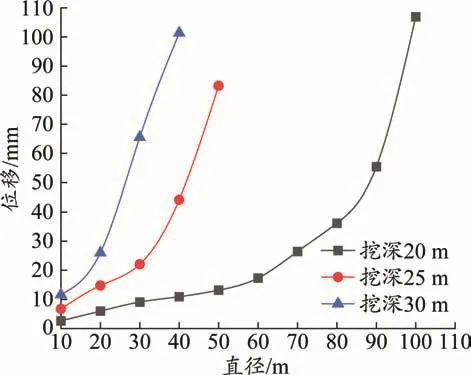
图4 不同直径下风化岩层基坑水平位移曲线

（4）基岩层稳定性分析

图5为基岩层基坑挖深20 m、25 m、30 m时，基坑水平位移随直径变化曲线。可以看出，随着基坑直径的增加，基坑水平位移近似线性增长，但位移值较小。当基坑直径为100 m时，水平位移最大，分别为1.34 mm、1.46 mm、1.60 mm。表明基岩在挖深20～30 m范围内，由于自身的物理力学特性，在“拱效应”随直径增加而减小的过程中，并未产生失稳破坏。

图5 基岩层基坑水平位移曲线

（5）总体分析

圆形基坑从结构上可以看作为闭合的拱，通过自身形成的“拱效应”，抑制土体的径向位移，使结构更加稳定［12］。当基坑直径较小时，“拱效应”显著，基坑较稳定；然而，当基坑直径较大时，环向的抑制作用减小，“拱效应”不显著，基坑在无支护情况下易发生失稳破坏。

综上，典型地层圆形基坑随直径不断增加至一定值时，由于“拱效应”的作用效果减小，导致基坑在无支护情况下发生失稳破坏，基坑失稳时的临界直径汇总见表2。

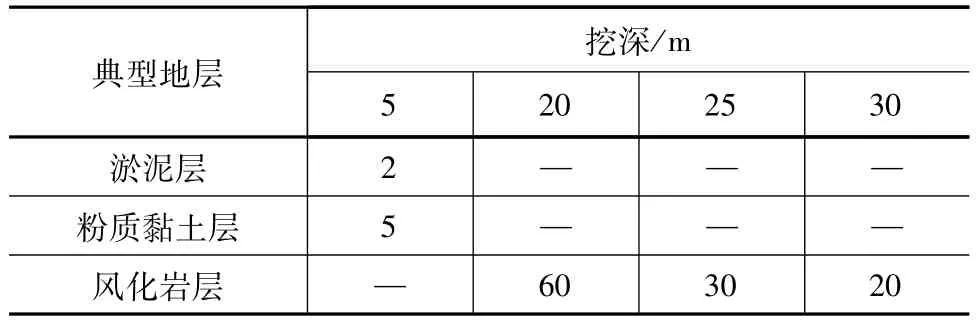
表2 不同挖深下典型地层基坑失稳时的临界直径

4 结论

通过数值模拟方法，在无支护情况下，随基坑直径不断变化，对相应典型地层基坑进行分析，并与基坑规范进行比较，以判断基坑的安全性。以采用的失稳判定标准和选取的地层参数为基础，经研究表明：

（1）不同典型地层下，基坑发生失稳破坏的临界直径不同。

（2）挖深5 m时，淤泥层基坑失稳的临界直径约为2 m，粉质黏土层基坑失稳的临界直径约为5 m。

（3）挖深分别为20 m、25 m、30 m 时，风化岩层基坑失稳的临界直径分别约为60 m、30 m、20 m。

（4）挖深20～30 m范围内，基岩层基坑水平位移呈线性增长，但未发生失稳破坏。

考虑到实际工程中基坑深度大多小于30 m，因而本文仅对挖深小于30 m的地层进行分析。