天津地区用电量与气温的非线性响应关系研究

兰辉 于佳卉 曹经福 刘玉坤 孙玫玲 黄鹤

(1.天津市气象服务中心，天津 300074; 2.天津市气象科学研究所，天津 300074;3.国网天津市电力公司，天津 300010; 4.天津市气候中心，天津 300074)

引言

准确预测用电量需求对电力能源供应规划和经济评估工作具有重要意义，而气温作为直接影响夏季降温和冬季取暖两大用电需求的气象要素，是预测模型中必须考虑的因素[1-3]。在以往的研究中，不同学者利用多种方法分析了气温和用电量之间的非线性特征[4-6]，确定了用电量与气温之间的响应关系，为建立合适的预测模型奠定基础。早期研究对于用电需求与气温之间的响应关系一般设定为“V”型[7]，即假设存在一个阈值气温，当气温超过该值，电能主要用于冷却降温，用电量随气温升高而升高(冷却区)，而气温低于该值，电能主要用于加热取暖，用电量随气温降低而升高(加热区)。有学者研究发现分段后中间的阈值气温实际上是一个温度区间[4,8]，在这个温度区间内，电力需求随气温的改变没有明显变化，并定义该温度区间为舒适区，从而形成了气温和用电量之间的“U”型响应关系模型。其中，用电需求与气温不同分段区域的关系曲线最多的为线性不对称模型和非线性模型[9]。

根据用电量和气温的不同响应关系，在用电量预测时广泛采用分段预测的思路，如常用的度日值预测方法[10-11]。由于分段阈值气温的选取会直接影响用电量需求模型的建立，因此，很多学者开展了专项研究。在“V”型响应关系中，通常将阈值气温选为18.3 ℃，Bessec和Fouquau[5]研究发现，欧洲15个国家的阈值气温存在明显差异；而在“U”型响应关系中,受社会环境、经济结构、建筑节能等因素的可能影响，不同地区的阈值气温也存在差异[10-13]。

虽然以往研究取得了大量成果，但大部分关于用电量与气象条件的非线性关系研究仅根据用电量预测的需要，对单一模型进行分析。国内则一般直接引入已有的阈值气温研究结果，而缺乏对本地适用性的分析。在阈值气温的计算中，多仅根据气温与用电量的响应关系确定，而未考虑其他气象要素的影响，也未考虑同一地区不同时段阈值气温的差异，从而导致阈值气温的计算结果产生偏差，进而影响用电量需求预测的准确率。针对以上问题，本文利用计量经济学上普遍应用的非线性滑动回归(STR)模型和门限回归(TR)模型，分析了“V”型非线性、“U”型线性和“U”型非线性3种模型下气温与用电量的响应关系，计算不同模型对应的阈值气温，并在此基础上，分析相对湿度对阈值气温的影响及同一区域阈值气温随时间的变化，为进一步开展气温累积效应和用电量需求分析等提供参考。

1 资料与方法

1.1 资料来源及处理

所用数据包括电力数据和气象数据。电力数据来自国网天津市电力公司，为天津市2002—2005年和2014—2019年逐日用电量数据；气象数据来自天津市气象局，为2002—2005年和2014—2019年天津市城市气候监测站(站号54517)的逐日平均气温、相对湿度及1960—2019年年平均气温数据，其中2014—2019年的电力和气象数据用于开展用电量与气象要素分析，2002—2005年电力和气象数据用于评估阈值气温随时间变化，1960—2019年年平均气温主要用于分析阈值气温改变的原因。由于国外多个研究[4-5,8]已论证非线性滑动回归(STR)模型和门限回归(TR)模型在确定阈值气温方面的适用性，因此，本文未选取检验样本开展评估工作。

为评估用电量与气象要素的非线性关系，需要剔除非气象因素对用电量产生的影响。根据Scapin等[11]的模型，用电量除受气象条件影响外，还表现出明显的周周期特点和长期趋势特征，模型具体公式为：

(1)

(2)

式(1)中，D为日用电量;t为日数;I为周周期的虚拟变量;V为气象因子;α、β和γ分别为系数;ε为残差。式(1)右侧第1项为用电量时间序列的趋势项，主要反映经济形势和消费习惯的长期变化对用电量的影响；右侧第2项代表用电量的周期性变化。有研究表明[4]，周二至周四用电量比较接近，周五略偏少，周一次之，周末最少，将I1在周一时设置为1，其他时间设置为0，以此类推，I2、I3、I4、I5分别在周二至周四、周五、周六、周日时设置为1，其他时间设置为0；右侧第3项代表气象条件影响下的用电量变化，主要受气温条件影响，由于最高、最低气温更适合预测日用电量的峰值和低谷[14]，因此本文采用平均气温作为预测因子用于预测日总用电量；右侧第4项为残差项。

采用二次曲线拟合用电量随时间变化趋势(右侧第1项)，并仅选取周二至周四的数据，以消除周周期变化(右侧第2项)对分析结果的影响。

1.2 用电量与气温关系的模型

1.2.1 TR模型

Hansen在门限回归模型(Threshold Regression Model，TR)上进行了大量研究[15-16]。先后提出时间序列门限自回归模型的估计和检验方法、具有个体效应的面板门限模型的计量分析方法、多元门限回归模型的思想等一系列创新性研究，并发展出一套完备的门限回归模型，其中Hansen的双阈值单元线性回归模型的计算公式为：

(3)

式(3)中，DF为气象用电量;MT为平均气温;μ为常数;ω为系数;ε为残差;t为时间;Th1和Th2分别为加热区与舒适区、舒适区与冷却区的阈值气温。

Moral-Carcedo等[4]利用式(3)计算得到用电量随气温变化的双阈值气温，通过建立3个线性模型，计算不同模型之间的交点(Th1和Th2)，即上下限的阈值气温。式(3)中假设加热区和冷却区的用电量与气温之间呈线性变化，对其进行调整，可以得到用电量和气温非线性响应关系下的双阈值气温，公式如下：

(4)

式(4)中，k为系数;其他各变量与式(3)一致。

1.2.2 STR模型

平滑转换自回归模型(Smooth Transition Auto-regression Model，STAR)是由GRANGER等提出的，目前已经形成了一套较为成熟的建模程序，包括模型的设定、估计和诊断测试，STAR模型的提出为非线性滑动回归模型(Smooth Transition Regression Model，STR)奠定了理论基础[17]。STR模型是对STAR模型的改进和发展，为模拟电力需求对温度的响应而提出的STR模型[4]可以表示为：

DFt=(α1+β1MTt)[1-G(MTt;γ,c)]+(α2+β2MTt)G(MTt;γ,c)+εt

(5)

式(5)中，εt为独立分布的误差，假设其服从正态分布;转换函数G(MTt;γ,c) 是一个取值范围为[0，1]的连续函数，常见的形式是logistic函数形式和指数函数形式，其中 logistic 函数形式的表达式为:

G(MTt;γ,c)=[1+exp{-γ(MTt-c)}]-1

(6)

式(6)中，MT表示平均气温;斜率γ反映了模型描述的状态“0”过渡到状态“1”的速度大小及转换的平滑性;c表示常数;t表示日数。式(5)和式(6)共同构成了logistic平滑回归模型，即LSTR模型。具体计算过程可参考昌春艳等[17]的研究成果。

1.2.3 模型评价方法

Hansen[15]以残差平方和最小化为条件确定门限值，本文采用类似的均方根误差确定最优阈值，均方根误差被广泛应用于模型检验[18-19]，公式如下:

(7)

分析结果时，出现两个临近阈值均方差相同的情况，本文采用决定系数辅助选取最优阈值，同时决定系数可用于对比不同时间段均方差较大的模型效果评估，公式如下[20-21]:

(8)

2 结果分析

2.1 用电量与气温关系模型

利用STR模型计算的2014—2019年天津市逐日用电量与气温“V”型非线性拟合曲线(图1)，利用TR模型计算的“U”型线性拟合和非线性拟合曲线(图2)，由于数据特征明显不符合“V”型线性拟合曲线，因此未计算该种情况下的阈值气温。分析可以发现，“V”型非线性响应关系下的阈值气温为18.8 ℃；“U”型响应关系下，线性和非线性模型的舒适区范围存在明显差异，其中线性曲线模型下的舒适区范围为12.3—23.4 ℃，非线性模型下的舒适区范围则明显变小，为13.7—21.7 ℃，这主要是由于非线性曲线可以捕捉用电量随气温增长幅度较小时的变化区间，而采用线性曲线，该区间被全部并入舒适区。

图1 2014—2019年天津市逐日用电量与气温“V”型非线性拟合曲线以及阈值气温Fig.1 Daily electricity consumption and temperature "V"-shaped nonlinear fitting curve as well as threshold temperature in Tianjin area from 2014 to 2019

图2 2014—2019年天津市逐日用电量与气温“U”型拟合曲线以及阈值气温Fig.2 Daily electricity consumption and temperature "U"-shaped fitting curve as well as threshold temperature in Tianjin area from 2014 to 2019

由图2可知，冷却区用电量随气温升高的速度明显大于加热区，在“U”型线性曲线中，加热区用电量随气温的增长率为-2.6 GWh/℃，冷却区用电量随气温的增长率为8.0 GWh/℃，同时冷却区的用电量峰值也明显偏大，这主要是由于夏季制冷主要由空调用电提供，而冬季加热则是由电力和天然气组合提供。除此之外，可以看出相较于舒适区与冷却区之间比较连贯的过渡，拟合曲线在“U”型线性关系模型下，加热区与舒适区之间的过渡并不连贯，这是由于天津市采用集体供暖的方式，在供暖季启停日期的前后，室外温度的变化不大，但用电量会出现明显变化，而该段时期的平均气温一般位于12.3 ℃左右，从而造成拟合曲线在舒适区和加热区之间的不连贯，而舒适区和冷却区之间的用电量主要受工业、商业和居民自发的用电行为影响，总体变化比较规律，因此拟合曲线在阈值气温处的用电量基本一致。

表1为各模型计算的2014—2019年天津市逐日用电量阈值气温及对应的预测效果，对比3种模型的预测效果发现，单阈值的非线性模型优于双阈值的线性模型，而双阈值的非线性模型优于单阈值的非线性模型，表明双阈值优于单阈值，非线性优于线性。

表1 2014—2019年天津市逐日用电量与气温在不同响应关系下的阈值气温及预测效果Table 1 Threshold temperature and prediction effect under different response relationships between daily electricity consumption and temperature in Tianjin area from 2014 to 2019

2.2 阈值气温的影响要素

2.2.1 相对湿度对阈值气温的影响

有研究表明，除了气温外，相对湿度对用电量的影响也十分显著[22-23]，有研究从体感温度或相对湿度角度分析阈值气温变化[7-8]。本文将所有数据按相对湿度范围分为3组，分别为30%—50%、50%—70%和其他，计算在“U”非线型模型(利用TR模型)中前两组的阈值气温，以评估相对湿度对阈值气温的可能影响。

2014—2019年天津市逐日用电量与气温拟合曲线在不同相对湿度范围内对应的阈值气温见图3，从图3可以看出，不同相对湿度下的舒适区存在明显差异，相对湿度在30%—50%时的舒适区范围明显大于相对湿度在50%—70%时的舒适区范围，特别是舒适区与冷却区的阈值气温，相差2.2 ℃，表明相对湿度对舒适区和冷却区的阈值气温影响较大，对舒适区和加热区阈值气温的影响则并不明显。

图3 2014—2019年天津市逐日用电量与气温拟合曲线在不同相对湿度范围内对应的阈值气温Fig.3 The threshold temperature corresponding to the daily electricity consumption and temperature fitting curve in different relative humidity ranges in Tianjin area from 2014 to 2019

值得注意的是，在冷却区中，当气温相同时，相对湿度为50%—70%时的用电量基本大于相对湿度为30%—50%时的用电量，而这一特点在舒适区和加热区不存在，用电量最大的日期也基本出现在相对湿度为50%—70%时，两种相对湿度范围内，冷却区内的用电量随气温变化曲线基本一致，这主要是二者在舒适区与冷却区的阈值气温差异较大，从而造成相同气温时，相对湿度为50%—70%时的用电量均高于相对湿度为30%—50%时。

由于日平均相对湿度低于30%及大于70%的样本数量偏少，本文未做详细分析。以往研究表明[22-24]，随着相对湿度增加，冷却用电量(或负荷)将明显上升，结合本文的研究成果，可以推测在相对湿度超过70%情况下，冷却区与舒适区的阈值气温将低于19.4 ℃，反之在相对湿度低于30%情况下，冷却区与舒适区的阈值气温将高于21.6 ℃。

2.2.2 阈值气温随时间变化特征

有研究表明，气候变化会对建筑采暖降温负荷产生影响[25]，为了探究气候变化可能对阈值气温的影响程度，选取2002—2005年的天津市逐日数据做相同的统计分析，以评估阈值气温随时间的变化，如表2所示。

表2 2002—2005年和2014—2019年天津市逐日用电量与气温在不同响应关系下阈值气温和预测效果对比Table 2 Comparison of threshold air temperature and prediction effect under different response relationships between daily electricity consumption and air temperature in Tianjin area between 2002-2005 and 2014-2019

由表2可知，在不同响应关系中，阈值气温均随时间发生了变化，利用STR模型计算“V”型非线性模型下的阈值气温从18.2 ℃增长到18.8 ℃，表明居民采取加热和冷却措施的气温向高温方向偏移。由图4可知，气温整体的变暖趋势非常明显，决定系数为0.825，每年增温幅度高达0.0689 ℃，按此增幅计算2002—2005年和2014—2019年的增幅约为0.9 ℃，与阈值气温变化幅度比较接近，这可能是由于人体适应环境的能力，造成舒适中值随全球变暖有所提升。

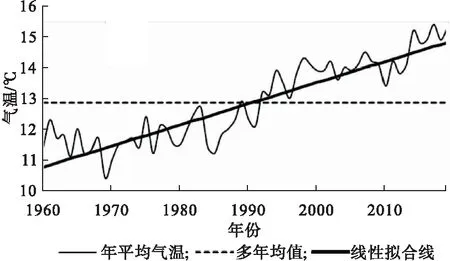
图4 1960—2019年天津市年平均气温变化曲线及趋势Fig.4 Annual average temperature change curve and trend in Tianjin area from 1960 to 2019

“U”型非线性模型在不同时间下的计算结果表明，2014—2019年的舒适区范围(13.7—21.7 ℃)较2002—2005年的范围(13.6—23.0 ℃)明显缩小，这主要是因为天津经济高速发展过程中，居民和商业调温设备大量增加，且人们对环境舒适的要求更高，而基本电价未发生明显改变，人们普遍会过早的采取加热或者降温措施，特别是降温措施(降低了1.3 ℃)。

同时，天津经济的快速发展、气候的持续变暖和居民用电习惯的改变还造成每年用电量的明显提升(2019年用电量为2002年用电量的3倍多)，而节能政策的推出与成果应用及相关产业的规模化发展，使得GDP的增速(2019年GDP为2002年的6倍多)明显大于用电量的增长，单位GDP需要的能耗明显减少。

3 结论与讨论

(1)本文运用计量经济学的两种方法计算了2014—2019年天津市用电量和气温在不同响应关系下的阈值气温，发现阈值气温存在明显差异，就日用电量预测效果而言，“U”型优于“V”型模型，非线性模型优于线性模型。

(2)相对湿度可对阈值气温产生较大影响，舒适区范围会随相对湿度增大明显减小，特别是舒适区和冷却区交界处的阈值气温，会随相对湿度增大向低温区偏移。

(3)对比2002—2005年和2014—2019年两段时间天津市用电量与气温不同响应关系下的阈值气温，发现阈值气温存在明显差异，这可能是由于经济增长和气候变化影响了居民用电习惯，从而引起阈值气温发生改变。

(4)在实际开展用电量和气象条件相关分析和预测时，应根据相对湿度范围分别计算阈值气温；当分析或者预测的数据时段较长，应分段选取不同的阈值气温。本文仅以天津为例，确定了用电量和气温在不同模型下的阈值气温，并分析了相对湿度和时间变化对阈值气温产生的影响，并未开展其他地区的对比研究。因此，需更多地区共同开展类似研究，从而发现相对湿度和时间变化对阈值气温影响更为普适性的规律。