不同大气稳定度下台风“莫拉克”（2009）的近地风场特性

李田田，屈宏雅，朱 蓉，李永平，汤胜茗，*

(1.中国气象局 上海台风研究所，上海 200030；2.同济大学，上海 200092；3.国家气候中心，北京 100081)

0 引 言

我国地处西北太平洋西岸，海岸线绵长，每年约有7～9个台风登陆我国，是全球台风灾害最严重的国家之一[1]。台风登陆时所致强风，以及脉动风结构和湍流特性与良态风相比存在显著差异，是防台减灾、工程结构抗风设计、风能资源评估的重要研究内容。

武占科等[2]分析了距地面200 m以上不同高度的台风脉动风特性，发现台风脉动风特性不宜采用良态风的统计值，台风实测风谱与规范谱有一定的偏差。胡尚瑜等[3]研究指出台风风场平均风速剖面指数、湍流强度和阵风因子均大于良态风场实测值。徐安等[4]提出台风脉动风速概率分布模型与风速大小有关，当风速较小时，脉动风速概率分布接近正态分布；当风速较大时，则与正态分布相差较大。Powell等[5]和Franklin等[6]基于GPS下投式探空数据，对台风边界层的平均风速剖面进行研究，发现在近地面层200 m高度内风速随高度的变化仍符合对数律。肖仪清等[7]依据近海面观测资料研究了台风登陆过程中风场特性，结果表明当下垫面为海面时，平均风速剖面指数与规范推荐值有较大差异。赵林等[8]通过分析超强台风“山竹”的近地外围风场风速剖面演变特性，发现台风远端风场S形和反C形2种风剖面形态，并提出Vickery模型对台风远端风场1.5 km高度范围内低空急流风剖面的拟合效果较好，但不能重现S形风剖面上部风剖面形态。王旭等[9]基于Kaimal互功率谱，提出了台风影响期间近地层纵向与竖向以及纵向与横向脉动风速分量之间的互功率谱修正模型，且与实测谱符合较好。Yu等[10]依据四个台风的观测数据进行功率谱分析，发现在低频时台风条件下的湍动能显著高于良态风条件下。王澈泉等[11]分析了城市地貌下台风影响期间不同时距的平均风速、湍流强度和阵风因子，结果表明，当平均时距较大时（＞5 min），湍流强度的均值较大且变异系数较小，湍流特性计算较为稳定。关于不同平均时距的问题，WMO规程[12]针对不同来流条件（陆地风、海洋风、离岸风、近岸风）建议了台风条件下采用不同平均时距（3 s，1 min，2 min，3 min，10 min，1 h）时阵风因子的转换关系，为不同平均时距的选择与转换提供了较为合理的依据和方法。Schroeder等[13]分析了七个登陆台风的移动观测数据，发现风向变化及来流方向地表粗糙度对风场特性影响较大，并且在台风眼墙或者最大风速位置，阵风因子和湍流强度略微降低，而湍流积分尺度却增大。Miller等[14]通过对多个观测站得到的十年台风数据进行研究，同样提出湍流强度和阵风因子受来流地形影响很大，还指出当下垫面从粗糙地形变到平坦地形时，至少需要1 km的距离才能使10 m高度的风在新地形下重新达到平衡。Mashiko和Shimada[15]研究了2015年台风“天鹅”的中心结构，发现当台风眼墙逼近观测站时，风速发生显著波动，3 s阵风可达64.3 m/s，阵风因子可达2.1。除了眼墙外，眼区内的平均风速、风向变化也比较剧烈，眼区中心的风速在0～10 m/s之间波动。更多研究[16-21]分析了台风影响期间的平均风速、湍流强度、极端风速、阵风因子、摩擦速度等风场特性的演变特征，但研究内容较少涉及大气稳定度对台风风场特性，特别是湍流特征的影响。

大气稳定度反应了大气湍流状态及稳定程度[22]。在良态风时，有研究表明[23-27]不同大气稳定度条件下平均风速剖面有显著差异，并有学者[25-26]根据不同稳定度条件建立不同风速剖面的修正模型。例如，对数律形式的风速剖面仅适用于中性大气边界层内[28]，若在非中性层结下应用，则需要采用稳定度修正函数对其进行修正[22,25]。Sathe等[29]对不同大气稳定度下风电机组所受载荷的差异进行研究，发现在稳定层结下，风电机组塔架受到的荷载比中性条件下减少17%；在不稳定层结下，荷载比中性条件减少3%。然而，对于风电机组转子受到的荷载却有相反的结论，考虑大气稳定度时得到的荷载比中性条件高12%。在台风条件下，王旭等[30]对台风“梅花”影响期间风场特性进行分析，发现中性层结下水平平均风速小于非中性条件下。柯清派等[31]对台风“黑格比”的实测数据进行分析时发现非中性层结出现频率达到64%，且考虑大气层结状况的风速剖面模型可以更好地刻画海面风场的风速分布。综上，目前关于大气稳定度比较成熟的研究多集中在良态风场，对台风影响期间非良态风场状态下大气稳定度对风场特性的影响研究比较匮乏。因此，本研究将基于台风“莫拉克”（2009），探究不同大气稳定度下台风风场特性的差异，填补这一研究领域的空白。

已有学者针对“莫拉克”做了一些研究。文献[32-35]对“莫拉克”登陆期间强度、结构、路径演变特征进行了动力学分析。李永平等[36]分析了“莫拉克”登陆过程中的地面阵风特性，发现地面阵风主要呈3～7 min周期性变化，且存在明显的相干结构。张容焱等[37]分析了“莫拉克”影响范围内的33座测风塔观测资料，研究发现阵风系数随高度变化与地形有关，一般情况下随高度升高而减小，在复杂地形条件下不符合随高度升高而减小的规律。关于“莫拉克”的已有研究也鲜少涉及台风影响期间大气稳定度的分析。

本研究利用近海岸一座120 m和两座100 m高的测风塔获得的2009年台风“莫拉克”数据，分析台风影响期间大气层结状况，台风风场不同高度的平均风速、平均风向、湍流强度、阵风因子和湍流积分尺度的演变规律，以及脉动风速谱的特征，以探究不同大气稳定度下台风风场特性的差异性，为防台减灾和工程结构抗风设计等提供参考。

1 “莫拉克”及观测试验概述

1.1 “莫拉克”概况

2009年第8号台风“莫拉克”（Morakot）于8月3日在西北太平洋生成，其最佳路径如图1所示，数据来源于中国气象局上海台风研究所[38]。“莫拉克”在2009年8月5日加强为台风级别，7日23:45（北京时间，下同）在台湾花莲首次登陆，登陆时近中心最大风力达13级（40 m/s），8日进入台湾海峡后向北偏折。图2（a）所示为8日16:00时“莫拉克”的雷达图像。“莫拉克”的结构呈现不对称性，台风眼区和眼墙区结构松散，强对流主要位于眼区以南和以东区域。为了辅助分析，“莫拉克”的最佳路径（红色实线）和相近时刻最大风速半径（红色虚线圆圈）也标注在雷达图中。最大风速半径数据来源于联合台风警报中心（JTWC）[39]。9日16:20“莫拉克”在福建霞浦再次登陆，登陆时中心附近最大风力达12级（33 m/s）。图2（b）为 9日16:00时“莫拉克”的雷达图像，以及相近时刻最大风速半径。此时，由于登陆影响，台风强度减弱，不对称结构更加明显。

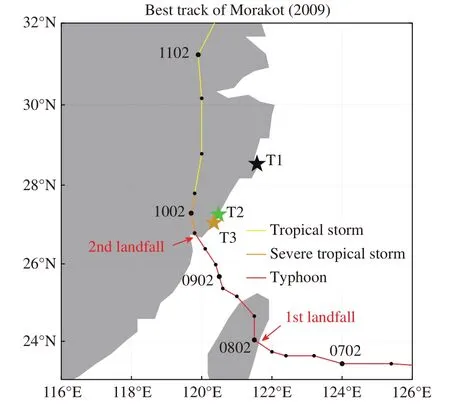
图1 “莫拉克”最佳路径及测风塔位置Fig.1 The best track of typhoon Morakot and locations of wind towers

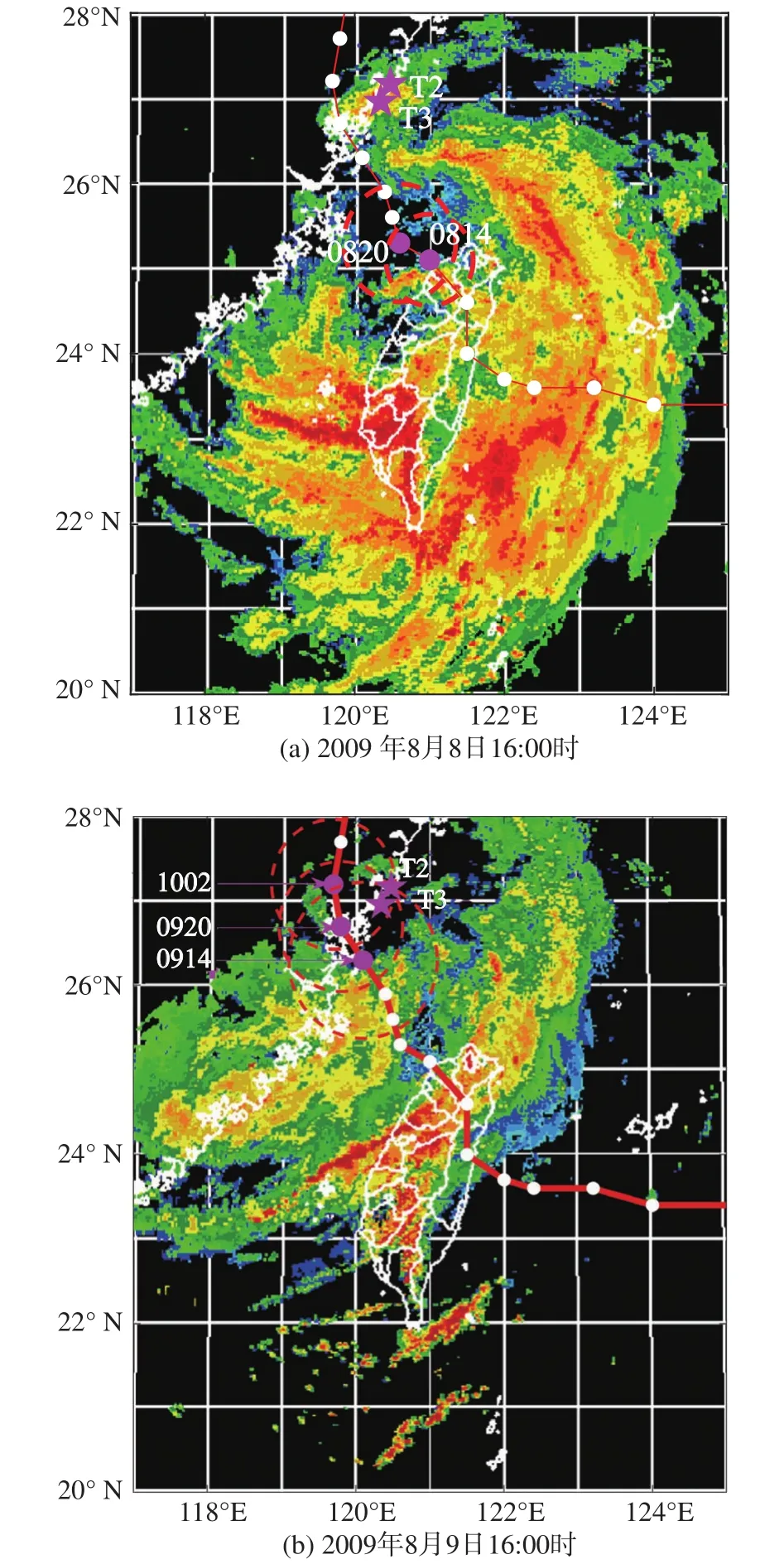
图2 “莫拉克”雷达图像Fig.2 Radar images of typhoon Morakot

1.2 观测试验

“莫拉克”观测采用英国Gill公司生产的WindMaster Pro型超声风速仪（图3），其在边界层湍流观测和风工程测量中应用广泛。该仪器使用环境温度为-40 ℃～+70 ℃；风速测量范围是0～65 m/s，测量精度为 0.01 m/s；风向测量范围是 0°～359°，测量精度为0.1°；数据采样频率为10 Hz。本研究数据测量时间范围是8月7日00:00时至8月11日00:00时。

图3 WindMaster Pro型超声风速仪探头Fig.3 A WindMaster Pro ultrasonic anemometer

如图1所示，在“莫拉克”中心经过的路径上，有三座安装超声风速仪的测风塔获取了该台风的风况数据。测风塔编号依次为 T1（121.57°E，28.44°N）、T2（120.48°E，27.17°N）和 T3（120.35°E，26.96°N），其距离台风中心的最短距离分别为158 km、76 km和59 km。测风塔T1位于浙江台州东海塘（图4（a）），风塔周边为村落、农田、沙地等平坦地形，风塔东面距离海岸线约11 km。塔高为120 m，塔基离海平面20 m，在塔的50 m、70 m、100 m和120 m四层高度分别安装了超声风速仪。测风塔T2和T3分别位于浙江温州霞关和福建福鼎嵛山岛，塔高均为100 m，并均在70 m高度安装了超声风速仪。其中，T2塔位于有树木的平缓山坡上（图4（b）），塔基离海平面53 m；塔的北面为山地地形，北向海拔较高且最高海拔约245 m；塔的西南和南面靠近海岸，最短距离约180 m；塔的东面距离海岸较远，约570 m。T3塔位于海岛上一条西北-东南走向的山脊上（图4（c）），塔基离海平面344 m；该处地势陡峭且有树木，东南向海拔较高，最高海拔约486 m；塔的北面距离海岸最近，最短距离约1.3 km。

图4 测风塔周边地表特征Fig.4 Surroundings of the wind towers

2 观测试验数据处理

2.1 质量控制及样本选择

为了避免台风登陆过程伴随的强降水对超声风速仪观测数据可能造成的影响，首先，根据超声风速仪的数据判别码去除无效数据。其次，依据文献[40-42]提供的方法，去除野点、随机脉冲等异常点（由于环境因子干扰、电源不稳定、湍流信号本身随机性等原因引发的异常信号），缺失的数据采用线性插值方法进行填补。台风登陆过程中风速时程常伴随非平稳过程，进行台风脉动特性分析时，将时间序列去掉趋势项[42-43]，并进行平稳性检验[44]，使得每个样本尽量满足平稳各态遍历随机过程的要求。最后，对“莫拉克”进行多样本分析，样本的平均时距取为10 min，每个样本包含600个数据。

2.2 数据代表性判别

图5给出了各个时刻三座测风塔与台风中心的距离，以及“莫拉克”的最大风速半径。结合图2的雷达图像，可以判断在2009年8月9日14:00时至10日02:00时之间（台风第二次登陆前后），测风塔T2、T3位于“莫拉克”的眼墙区或者最大风速位置，在其他时刻位于外围雨带区。测风塔T1则一直位于“莫拉克”的外围雨带区。为了进一步确定台风核心强风区域是否经过观测点，依据以下两点进行判别[45-46]：一是测风塔获取的台风强风（17.2 m/s以上）风向角应出现大幅度的转换；二是台风过程的风速时程曲线呈“M”型变化，即强风出现双峰型分布，双峰之间的底部（为台风眼区）出现小于11 m/s的风速，即可判断为台风眼区经过。从图6“莫拉克”经过测风塔时10 min平均风速、风向的时程变化曲线可以看出，风速时程曲线最大风速低于17.2 m/s，且没有明显的“M”型变化，因此不满足以上两条判别条件，不属于台风眼区。综上所述，测风塔T1的观测数据代表台风外围风场特性，测风塔T2和T3的数据代表台风外围和眼墙边缘风场特性。

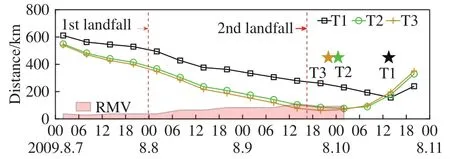
图5 各时刻台风中心与测风塔距离及“莫拉克”最大风速半径RMV（★对应台风中心距离测风塔最近的时刻，下同）Fig.5 Distances between the typhoon center and wind towers and the radius of maximum velocity (RMV) of typhoon Morakot(★ indicates the time instant when the typhoon center is closest to the wind tower)

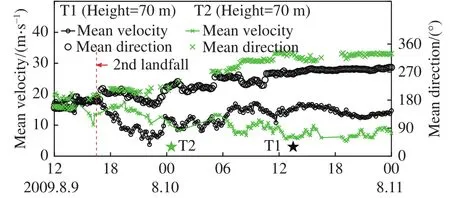
图6 “莫拉克”穿过测风塔前后10 min平均风速、风向时程曲线Fig.6 Time histories of 10 min-averaged horizontal wind velocity and direction when Morakot passes wind towers

2.3 数据处理

超声风速仪x、y、z三个方向测得的三维风速时间序列分别为ux(t)、uy(t)和uz(t)。以10 min为时距进行分析，水平平均风速U和水平平均风向角 θ根据公式（1-2）进行计算。

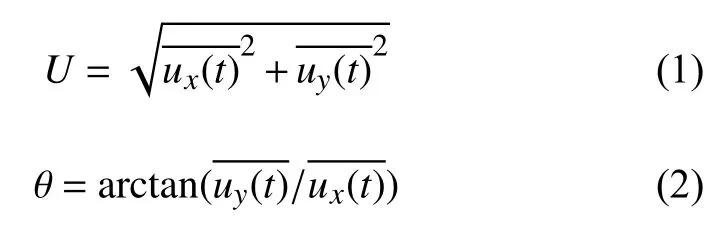
竖向风速方向与风速仪z坐标轴相同，因此竖向平均风速W为：

在平均时距内，顺风向脉动风速u(t)、横风向脉动风速v(t)和竖向脉动风速w(t)根据公式（4-6）计算。

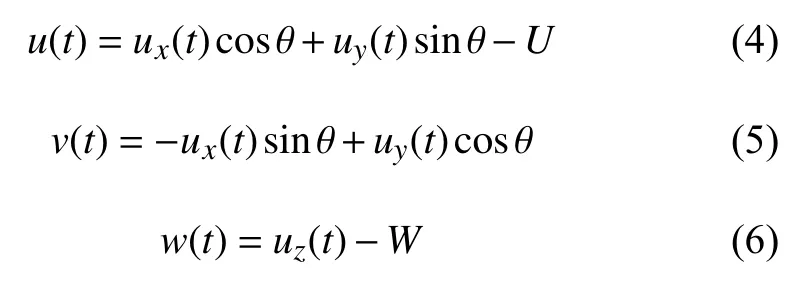
湍流强度I定义为平均时距内脉动风速均方根与水平平均风速的比值，其表征台风的脉动强度，是确定结构所受风荷载的关键参数之一。

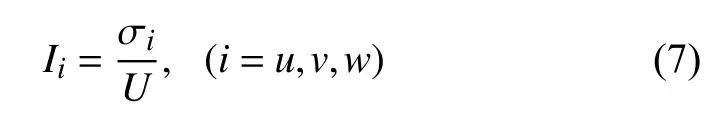
式中：σi分别表示脉动风速u(t)、v(t)、w(t)的均方根，U为10 min时距内水平平均风速。

阵风因子G也可表征台风的脉动强度，定义为平均时距内阵风持续时间为 τ的平均风速最大值与平均时距内的水平平均风速之比，即公式（8-10），其中 τ取为3 s。

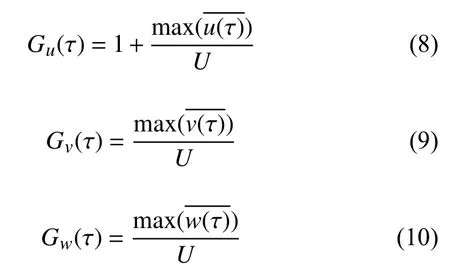
湍流积分尺度l用来描述风场中湍流涡旋平均尺度，根据Taylor假设[47]用自相关函数进行计算：

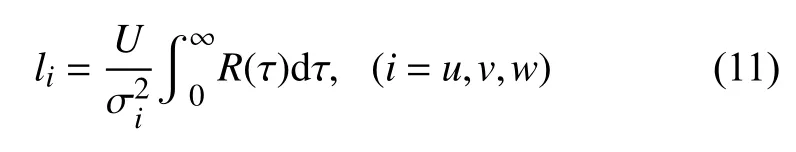
式中：R(τ )为脉动风速的自相关函数。

脉动风速谱S(n)在频域上表征了台风的脉动特征，描述了湍动能在不同尺度水平上的能量分布。其也是结构抗风设计的重要参量之一。有研究表明[7,9,16]，von-Karman谱能够较好地反映台风实测结果，其顺风向脉动风速谱函数表示为：

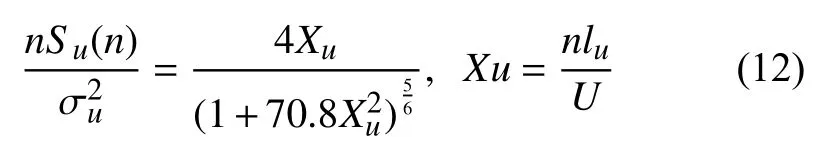
大气稳定度反应了热力因子（浮力对流）与动力因子（雷诺应力）对湍流作用的相对重要性。大气运动时，湍流状态的维持既有浮力也有雷诺应力的作用。雷诺应力做功表现为风剪切导致湍流的机械产生，其值始终为正。浮力作用基于对流的产生与否可加强或抑制湍流，因此浮力做功可正可负。在中性层结条件下，浮力影响可以忽略不计，空气流动主要由大气边界层底层地形和粗糙度等导致的机械湍流控制，此时，对数律形式的风速剖面规律仍可保持。在稳定层结条件下，空气反抗负浮力做功消耗湍流能量。相反地，在不稳定层结下，浮力做正功，且浮力作用逐渐超过动力影响占据控制优势，引起对流混合，增强湍流能量。因此，对于大气稳定度的判别，可根据浮力做功和雷诺应力做功的相对大小来确定。目前常采用梯度理查森数Ri[25]和莫宁-奥布霍夫长度L[48]两种参数作为稳定度的判据。Ri可根据两个高度之间的温度和风速梯度进行计算，不需要湍流脉动测量结果。L的计算涉及摩擦速度、竖向温度通量等湍流数据，需要借助三维超声风速仪、涡动系统等测量设备。本研究的观测数据系由WindMaster Pro型超声风速仪获得，由此选择更为贴近的莫宁-奥布霍夫长度法对大气层结状况进行判定，L的计算公式如下。

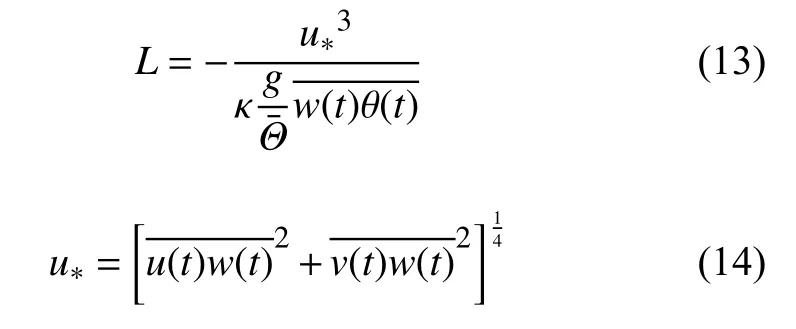
式中：u*为摩擦速度；κ为卡曼常数，取0.4；g为重力加速度，取 9.8m/s2；为10 min时距内平均温度；θ为温度脉动，表示10 min时距内平均温度竖向通量。由文献[26]可知：当 |L|≥500 m时，大气处于中性状态；当10 m＜L＜500 m时，大气处于稳定状态；当–500 m＜L＜–50 m时，大气处于不稳定状态。

3 结果分析

3.1 大气稳定度

大气稳定度的判别可根据莫宁-奥布霍夫长度L来确定，但当大气处于中性状态时，L可能趋于无限长，考虑实用中的便利性，常用无因次量z/L来代替L作为稳定度的度量。相应的判别准则变为：当-0.002z≤z/L≤0.002z时，大气处于中性状态；当z/L＞0.002z时，大气处于稳定状态；当z/L＜-0.002z时，大气处于不稳定状态。因此，测风塔50 m、70 m、100 m、120 m不同观测高度对应的判别大气稳定度的阈值分别为±0.1、±0.14、±0.2 和±0.24。例如在 50 m 高度时，当 - 0.1≤z/L≤0.1 时，大气处于中性状态；当z/L＞0.1时，大气处于稳定状态；当z/L＜-0.1 时，大气处于不稳定状态。

图7为“莫拉克”影响期间大气稳定度随时间的变化历程。表1统计了不同稳定度出现的频率。其中，测风塔T2在台风第二次登陆前后、测风塔T3在第一次登陆后，数据缺失相对较多，因此，以测风塔T1为主进行大气稳定度的相关分析。从图7和表1可以看出，中性层结状况出现频率最高（52%～64%），主要集中在台风第一次登陆前；不稳定层结主要出现在台风登陆前后及台风穿过测风塔时；稳定层结主要出现在台风第二次登陆前。不同高度上大气稳定度分布略有不同。在50 m高度时，不稳定层结出现频率高于稳定层结；而随着高度的升高，稳定层结出现频率逐渐增大，从18%增大到35%，不稳定层结出现频率逐渐减小，从30%减小到10%。说明低空大气由于受地表热量和摩擦影响趋于不稳定，而高空大气受影响较小趋于稳定。

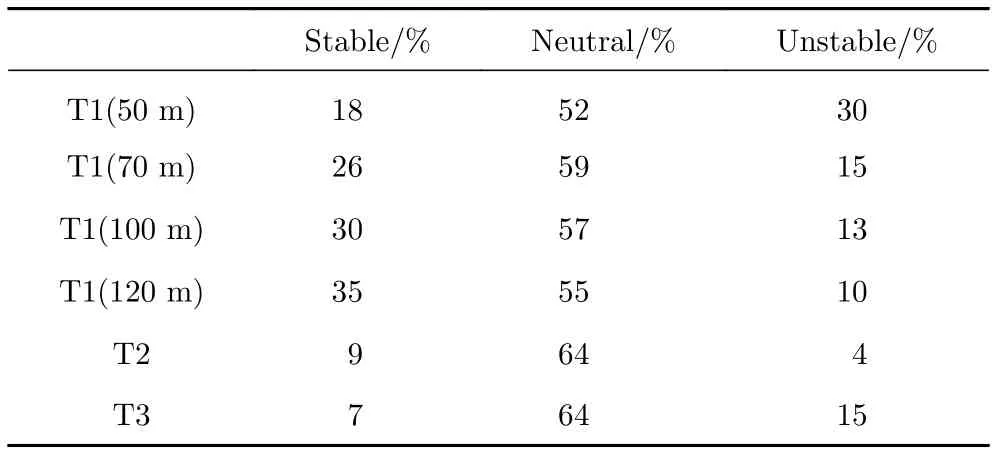
表1 台风“莫拉克”期间不同大气稳定度出现频率Table 1 The occurrence frequencies of different atmospheric stability conditions during the passage of typhoon Morakot

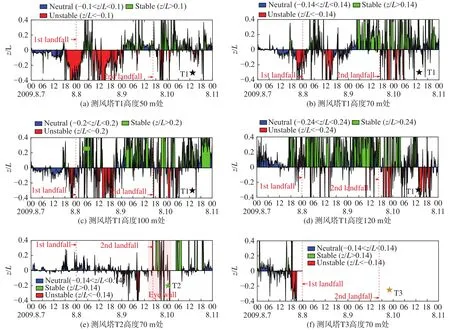
图7 大气稳定度随时间变化历程Fig.7 Time histories of the atmospheric stability

3.2 平均风速、风向

基于实测数据，以10 min为时距计算的平均风速、风向如图8所示。测风塔T1在50 m、70 m、100 m、120 m四层高度的平均风速、风向随时间演变规律基本一致。“莫拉克”在第一次登陆前后，风速在10～17 m/s（6～7级风）之间变化，总体变化较为平缓，风向东南和正南。此后，由于台风越来越靠近测风塔，风速开始缓慢增加，风向基本保持南风。在台风第二次登陆前，风速有较大波动，在登陆后，风速明显减小，直至距测风塔T1最近时，风速再次增强，风向逐渐由南风转为西风为主。测风塔T2的平均风向在第一次登陆前后以东南风为主，在第二次登陆后，风向转为西风和西北风。测风塔T2的平均风速总体呈现比T1塔更为明显的增强-减弱趋势，在9日00:00时和7:00时附近风速达到最大，超过25 m/s（10～11级风），分析是由于台风螺旋雨带区的影响（图2（a））以及眼墙区的逼近，使得风速增强，并且T2塔距离台风眼墙更近，风速增强更为明显。但在第二次登陆后，风向转为西风和西北风，此时风从陆地吹向海洋，虽然T2塔仍距离台风眼墙区较近，但由于海拔较高的山地地形和树木等遮挡，其风速逐渐减弱，甚至低于T1塔风速。测风塔T3由于仪器原因，只获取了7日台风数据。平均风速最大值为31.2 m/s（10～11级），大于同时期T1和T2塔测得的风速值，这是由于T3塔位于海拔较高的海岛上，山地地形的加速效应使得风速迅速增强。三座测风塔均位于台风中心行进方向的右侧，风向均呈顺时针旋转，与张容焱等[37]研究结果一致。

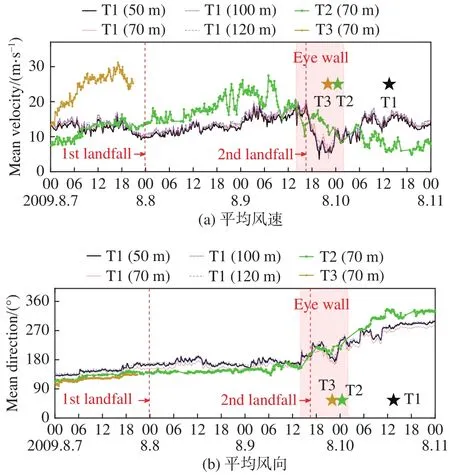
图8 10 min平均风速、风向随时间变化历程Fig.8 Time histories of 10 min-averaged horizontal wind velocity and direction

将测风塔T1不同稳定度条件下平均风速出现的频数进行统计，如图9所示。在所有高度上，中性层结条件下，平均风速为12～14 m/s出现频率最高。低空时，不稳定层结下，10～12 m/s出现频率最高；稳定层结下14～16 m/s出现频率最高。但高空时，不稳定层结下出现频率最高的平均风速逐渐变为14～16 m/s，稳定层结下变为12～14 m/s。风速为18～20 m/s时，50 m高度中性层结下样本数最多，70～120 m高度稳定层结下样本数最多，这一现象与王旭等[30]认为当平均风速较大时大气层结近似趋于中性有差异，可能原因是文献[30]中观测高度仅为40 m，结论或许有一定的局限性。将平均风向在不同稳定度条件下出现频数进行统计，发现中性层结下以东南风和南风为主，稳定和不稳定层结下以南风为主。

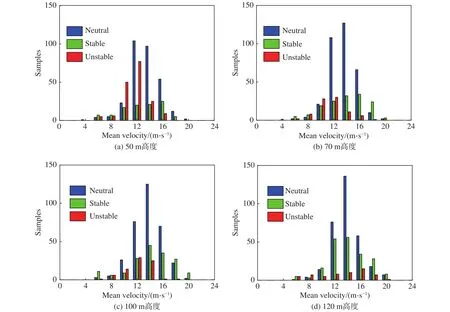
图9 不同稳定度条件下平均风速出现频率（测风塔T1）Fig.9 Occurrence frequencies of 10 min-averaged horizontal wind velocity under different atmospheric stability conditions at Tower T1

3.3 湍流强度

根据各测风塔的平均风速及风速标准差的台风样本，统计分析了“莫拉克”影响期间湍流强度的分布规律（图10）。测风塔T1测得的湍流强度在四层高度上的变化趋势基本一致，这里仅给出50 m高度结果。总体上，顺风向湍流强度高于横风向和竖向。台风第一次登陆时，由于台风中心距离测风塔较远，湍流强度变化较为平缓；第二次登陆时，湍流强度变化剧烈，湍流强度最大值达到53%。测风塔T2的湍流强度在7日白天较大，而后逐渐减小，在台风穿过测风塔时，幅值再次增大。这种减小-增大的变化趋势与T2塔的平均风速增强-减弱的变化趋势较为一致。这是因为湍流强度计算时采用水平平均风速进行标准化处理，所以随着风速的增强，湍流强度反而减弱。在“莫拉克”眼墙区影响时段，湍流强度略微降低，与Schroeder等[13]结论一致。在10日12:00-24:00期间，T2塔的横风向湍流强度大于顺风向，说明有树木和地形遮挡的离岸风对湍流脉动强度的分布有较大影响。测风塔T3的湍流强度与T2塔变化规律一致，但幅值偏小，同样是由于T3塔处的水平平均风速比T2塔大导致。

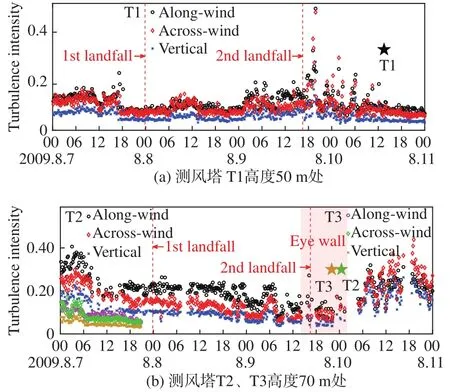
图10 湍流强度随时间变化历程Fig.10 Time histories of the turbulence intensity

测风塔T1测得的湍流强度在不同稳定度条件下出现的频率在各高度上一致，图11仅展示50 m高度结果。在中性层结条件下湍流强度主要分布在8%～16%之间，且出现频率分布相对均匀，在非中性层结条件下8%～10%出现频率最高。

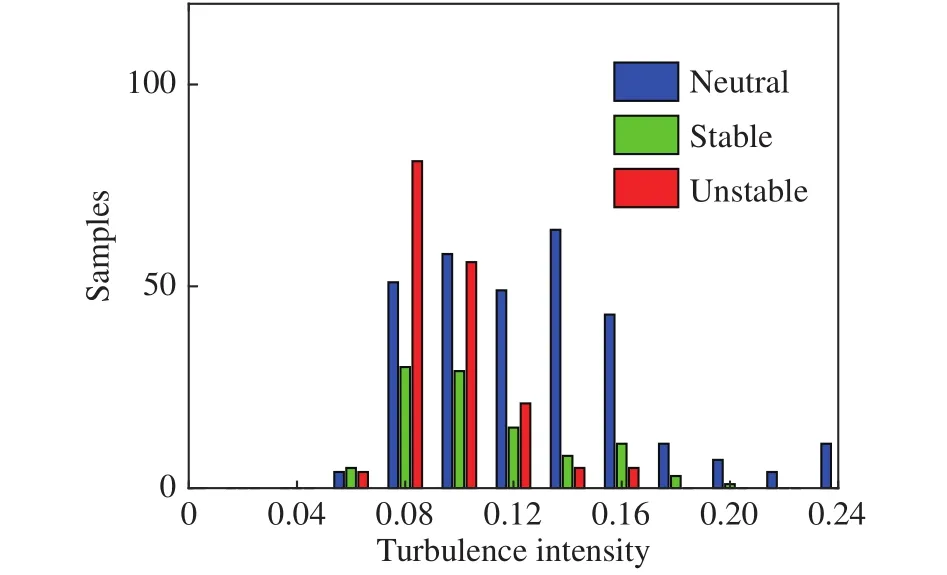
图11 不同稳定度条件下湍流强度出现频率（测风塔T1）Fig.11 Histograms of the turbulence intensity under different atmospheric stability conditions at Tower T1

3.4 阵风因子

“莫拉克”影响期间，阵风因子随时间的演变规律如图12所示。测风塔T1在四层高度上的变化趋势基本一致，这里仅给出50 m高度上结果。顺风向阵风因子在1.0～1.5之间变化，在台风第二次登陆时，波动较大，最大值可达2.4。T2塔阵风因子总体演变规律与湍流强度类似，先减小后增大；在眼墙区影响时段内，阵风因子相对较小。阵风因子和湍流强度在眼墙区影响时段内均未出现类似T1塔的剧烈波动，可能是由于数据缺失的原因，未能正确反应真实台风风场特性。T3塔阵风因子趋势与T2塔类似，但幅值偏小。不同稳定度条件下阵风因子出现频率与湍流强度出现频率趋势一致。

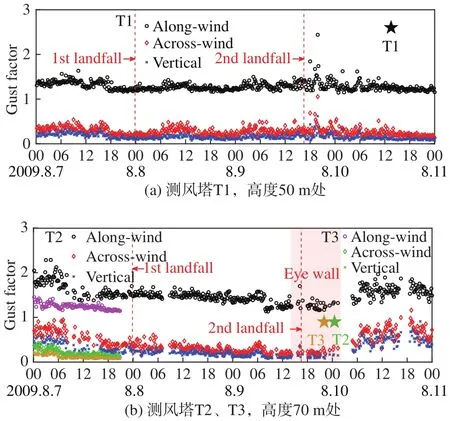
图12 阵风因子随时间变化历程Fig.12 Time histories of the gust factor

3.5 湍流积分尺度

图13给出了“莫拉克”的湍流积分尺度随风场发展的变化情况（测风塔T1仅给出100 m高度上结果）。总体上，顺风向湍流积分尺度最大，竖向最小。就测风塔T1和T2而言，在9日00:00时至台风第二次登陆前后，湍流积分尺度变化剧烈，且横风向与顺风向幅值相当，分析是由“莫拉克”逐渐靠近观测点以及台风登陆等导致，顺风向和横风向湍流涡旋尺度相当。从T3塔的积分尺度分布来看，其值在0～1 000 m之间变化，分布比较离散，说明下垫面为陡峭山地地形时，台风非平稳性较强，湍流积分尺度较大。在不同稳定度条件下，湍流积分尺度的频率分布趋势基本一致，且100 m积分尺度均出现频率最高（图14），说明大气层结状况对湍流积分尺度频率分布影响不显著。这可能是因为计算积分尺度所用的自相关函数法基于“Taylor假设”，适用于均匀平稳的纯机械湍流（中性层结条件）[45]，所以未能充分反映不同层结状况的影响。

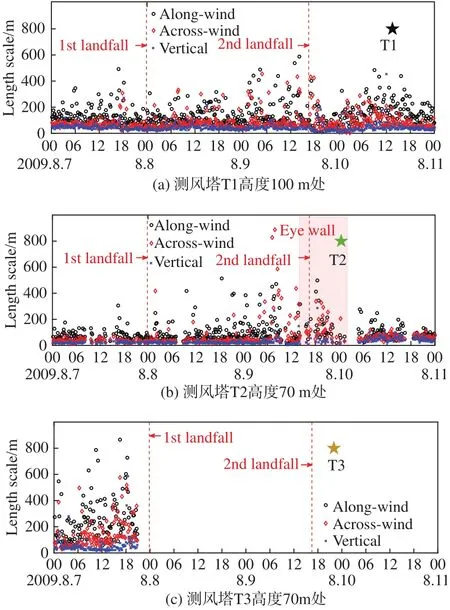
图13 湍流积分尺度随时间变化历程Fig.13 Time histories of the integral length

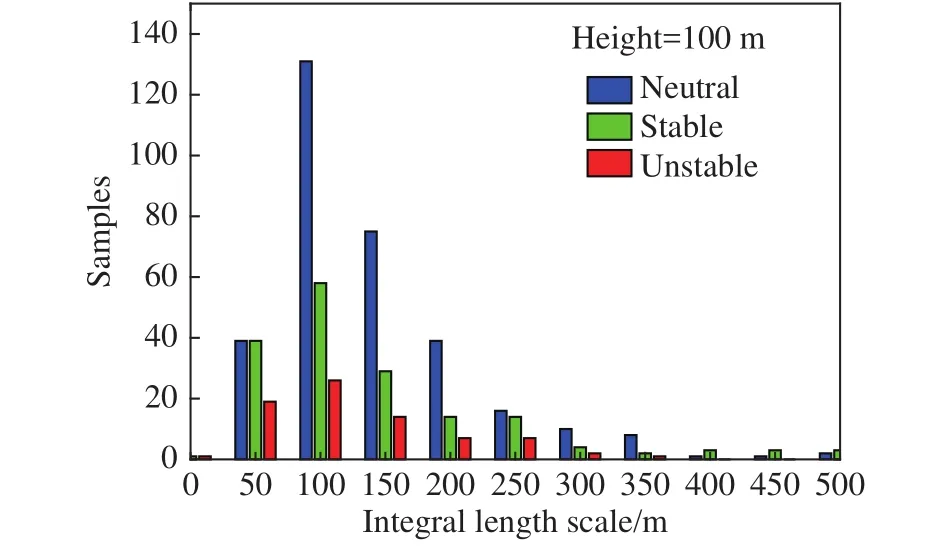
图14 不同稳定度下湍流积分尺度出现频率（测风塔T1）Fig.14 Histograms of the integral length under different atmospheric stability conditions at Tower T1

3.6 脉动风速谱

图15为不同稳定度条件下脉动风速谱及与von-Karman经验谱的对比。由于工程结构通常关心台风登陆后对结构产生的风荷载效应，所以此处针对测风塔T1和T2，选取台风登陆后的10 min时距脉动风速谱，其中T2塔的样本还位于台风眼墙区影响时段内。从图15可以看出，在中性层结条件下，脉动风速谱与经验谱吻合较好，在1～5 Hz频率范围内基本符合Kolmogorov的局地均匀各向同性湍流理论[22]，即在惯性子区内风速谱基本满足-2/3次方律，湍流脉动具有统计相似性。在非中性层结条件下，脉动风速谱与von-Karman谱存在一定偏差。对于测风塔T1，在稳定层结条件下，小于0.2 Hz频段von-Karman谱略高估了风速谱的能量，而大于1.5 Hz频段则低估了谱能量；在不稳定层结下，小于 0.3 Hz频段谱能量被高估，而大于0.8 Hz频段被低估。对于测风塔T2，在稳定层结下，小于0.2 Hz频段von-Karman谱高估了风速谱能量，大于1 Hz频段则低估了谱能量；在不稳定层结下，小于0.1 Hz频段谱能量被略微高估，而大于1 Hz频段则被低估。位于眼墙区的风速谱（T2塔）与外围区的风速谱（T1塔）相比，高频区风速谱能量在中性层结下偏低，在稳定层结下偏高，在不稳定层结下相近。从工程结构抗风设计所关注的高频段（＞0.2 Hz）来看，经验谱基本可以描述中性条件下台风实测谱，而在非中性条件下存在低估谱能量的情况。此外，台风不同位置的风速谱在高频区的能量分布也存在差异。

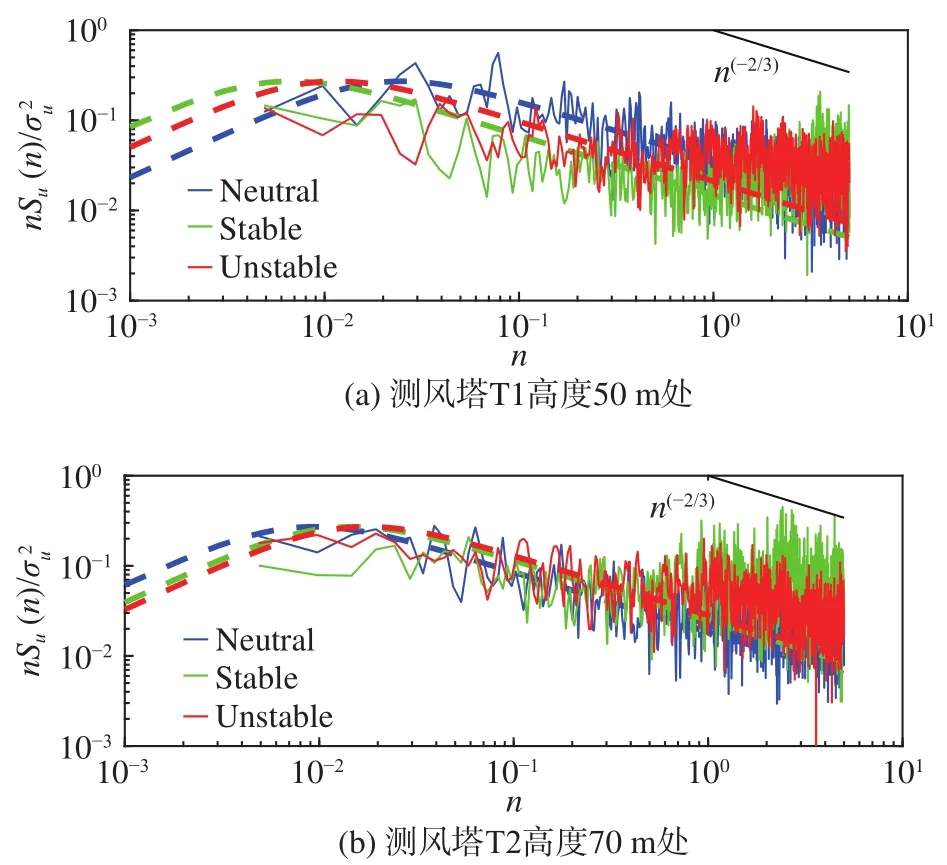
图15 实测纵向脉动风速谱与经验谱的比较（虚线代表von-Karman经验谱）Fig.15 Comparisons between the empirical and measured power spectra of the fluctuating longitudinal wind speed.Dashed lines represent von-Karman spectra

4 结 论

以往关于台风影响期间大气稳定度对风场特性的影响研究多集中在风速剖面模型的刻画上，而对台风风场湍流特征和脉动风速谱的研究较少。然而，湍流强度、阵风因子、风速谱等参数与结构所受风荷载、结构效应分析密切相关，对结构抗风设计起着重要的作用。基于此，本文依据2009年台风“莫拉克”风场的实测数据，分析了台风影响期间大气层结状况及不同大气稳定度下近地面风场特性，以探究大气稳定度对台风风场特性的影响。得到的结论如下：

1）在台风外围雨带区，非中性层结出现频率约44%，主要出现在台风登陆前后及台风外围穿过测风塔时。当平均风速较大（18～20 m/s）时，随着高度的增加，大气层结由中性渐趋于稳定。这与先前研究认为平均风速较大时大气层结近似趋于中性有差异。进行高层建筑、输电塔等结构设计时，需注意沿高度方向上大气稳定度的分层特性。

2）不同稳定度条件下平均风速、湍流强度、阵风因子的分布规律有显著差异，但平均风向和湍流积分尺度差异较小。由于风速与湍流强度等与结构风荷载的确定直接相关，且已有设计理论多基于中性层结假定，因此需注意非中性层结下这些参数的差异性及对风荷载计算的影响。

3）在中性层结条件下，脉动风速实测谱与经验谱（von-Karman谱）吻合较好。而在非中性层结下，实测谱比经验谱在低频段湍动能偏低，在高频段偏高。在工程结构所感兴趣的高频区（＞0.2 Hz），经验谱存在低估谱能量的情况，因此，在非中性层结条件下，有必要对经验谱依据大气稳定度进行修正后应用，以防工程结构抗风设计时存在安全隐患。

本研究以“莫拉克”台风为背景，分析了台风影响期间不同大气稳定度下近地面风场特性，但仅涉及一个台风实例，且观测位置距离台风中心较远，以上结论为初步分析事实，仍需要更多的台风实测数据来进行验证。在此基础上，下一步计划进一步探究不同大气稳定度下近地面风场特性产生差异的原因，以及考虑不同稳定度条件的平均风速、湍流强度、阵风因子、脉动风速谱的数学表达，为工程结构抗风设计等提供理论依据。