基于M估计的三维容栅微小位移系统参数估计
2021-09-16金怀智李新娥杨伟艺
金怀智,李新娥,王 睿,杨伟艺,顾 攀
(中北大学 电子测试技术重点实验室,山西 太原 030051)
0 引 言
微小位移测量经过多年的研究取得了长足的发展,是精密测量技术的研究热点之一[1],测量方法有以下几种:激光传感器、LVDT传感器、PSD位置敏感器件、电容位移传感器等[1,2]。本文所测系统为三维容栅位移系统,主要特征是容栅传感器电极呈栅极分布,具有测量精度高、运行速度快、体积小、结构简单、总体功耗低等优点,是狭小空间微小位移测量的理想仪器[3]。
最小二乘法(ordinary least square,OLS)是对未知参数估计的强大数学工具,具有无偏性和有效性[4]。最小二乘法在解决目标函数最优解问题时,会人为地忽略误差方程系数矩阵中的随机误差,这种含有离群值的线性估计,结果会受到不良影响,甚至产生错误结论,因此需要一种稳健回归解决上述问题。
对现有线性回归模型进行研究,提出使用M估计加权最小二乘法线性回归分析三维容栅微小位移。通过理论推导确定基本模型,并对测量位移进行正态性分析,确保模型为线性系统;采用Huber robust函数作为加权函数,具有较高的稳健性和估计效率;使用皮尔逊相关系数分析法验证测量值和预测值的相关性。实验测试结果表明,该算法在有离群值时具有良好的拟合效果,系统参数估计更准确、稳定,对三维容栅微小位移系统的安装调试具有显著指导作用。
1 测试系统设计
1.1 传感器设计
容栅传感器由多条平板电容并联,主要的工作部件为静栅和动栅[5],如图1所示。当动栅忽略边缘效应时,单块栅极的初始电容和正对面积记为C0和S0,容栅传感器的电容为
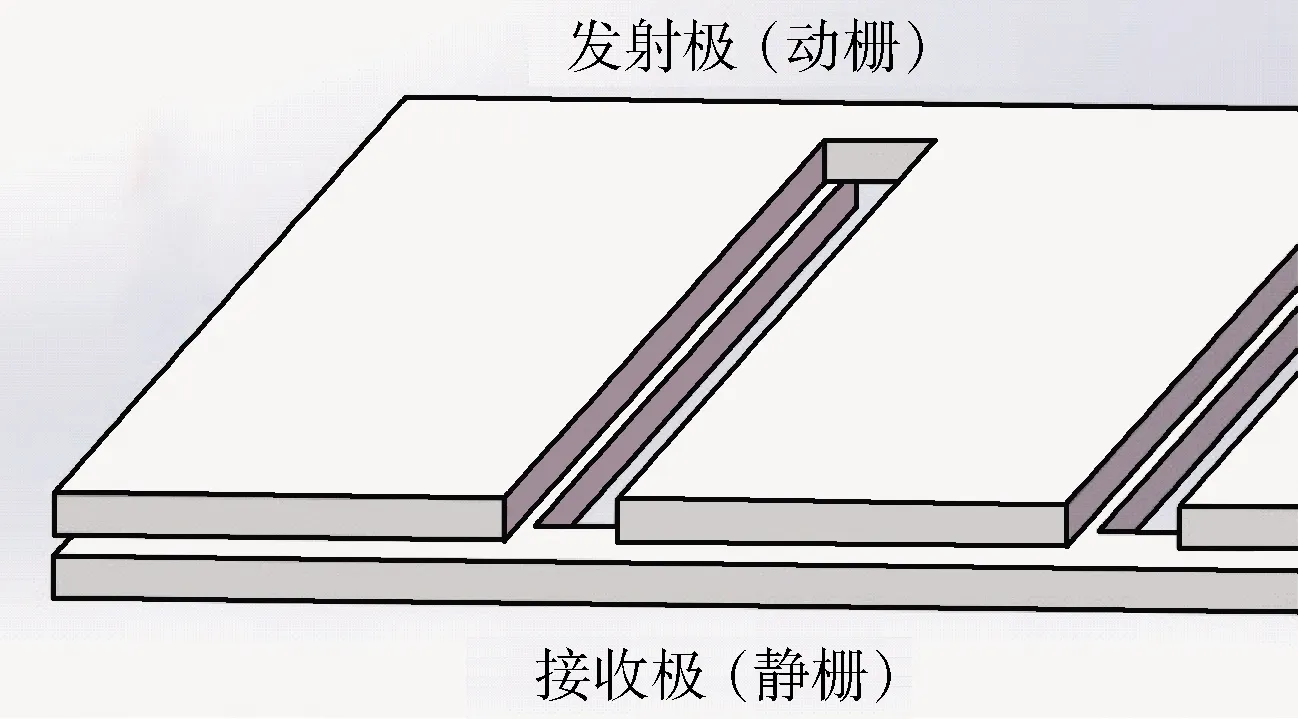
图1 容栅结构
(1)
式中:n为传感器栅极条数,ε0为真空介电常数,近似为8.854×10-12F/m,εr为板级间介质的相对介电常数,ε为总体介电常数,S0为单条栅极极间相对面积,S为总极间相对面积。
1.2 信号采集单元
本设计共有3个通道,分别是通道1(动栅X)、通道2(动栅Y)、通道3(动栅Z),安装在其中一个同心球外侧,代表着XYZ这3个方向的位移,其共同的静栅被安装于另一个同心球内侧。
三维容栅微小位移测试系统信号采集单元原理框架如图2所示。
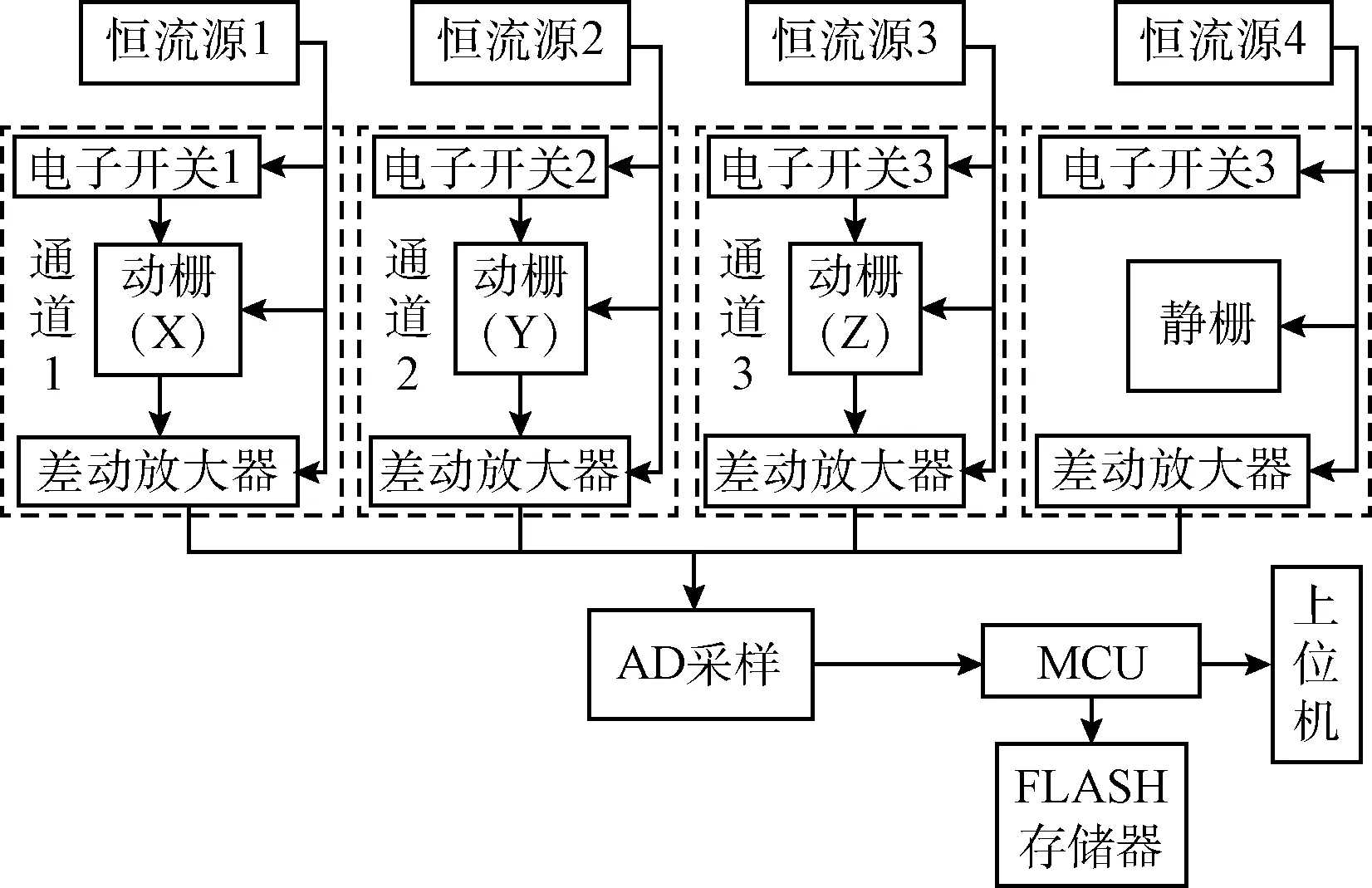
图2 采集单元原理框架
4个恒流源给容栅传感器供电,使用电子开关开阖传感器。由于容栅传感器的电容变化量很微小(约为1 pF/0.05 mm),电磁干扰,温度变化引起的噪声信号会在单路放大器输入端产生共模干扰。采用差分放大电路可以很好地解决这个问题,达到放大差模信号、抑制共模信号的目的。
任一通道电容与电压的关系
(2)
式(2)和式(1)联立得
(3)
式中:U为传感器两端模拟电压,Q为直流源输出电荷量。
本设计通过电子开关实现PWM波开关控制,当动栅发生位移造成相对面积的改变所引起的电容值变化,可判断微小位移的大小及方向。
1.3 传感器安装与布置
三维容栅传感器微小位移测量系统是为了测量两个同心球的相对转动情况,容栅传感器具有结构轻薄的特点,可以便捷安装在球体表面和内侧。
据文献[2]中对二维容栅微小位移系统的研究,三维传感器采取正交式安装方法,以XY坐标轴形成一个平面,再向上取一个与XY都正交的Z轴,形成三维坐标系。容栅传感器布置在两个同心球体表面,由于球面具有较大曲率,故安装传感器时可将其等效为4块平面容栅传感器,其中一个球面内侧安装一块接收级(静栅),另一个球面外侧安装3块相互正交的发射极(动栅),每一组动、静栅测量一个方向的位移变化,如图3(a)所示。

图3 容删安装及改进
实际安装时,当动、静栅均采用方形的容栅传感器时,拿X通道分析,初始相对面积为Sx0,静、动栅边长为L,三通道位移分别为x、y、z,由于容栅传感栅极间的d由同心球间距决定,分析时认为d为定值,其电压模型为
(4)
式(4)在模型分析时,X通道的电压涉及两个方向的位移,模型参数较为复杂,不适合在操作现场做参数估计。为了避免不同通道位移相互影响,使用3块10 mm×10 mm的静栅,与先前无异,成品字形排布;使用3块5 mm×10 mm的动栅,宽度缩小一半,当Z方向发生位移时,X通道由于静栅宽度大于动栅宽度,在量程范围内(0.3 mm~1 mm)Z方向的位移不对ΔSX产生影响,改进后的安装布置如图3(b)所示。
2 参数估计算法
2.1 模型分析
3个通道相互独立,对通道X做分析,根据式(4)可知其电压位移模型为
(5)
其中,k=Q/ε,x、y、z为3个方向的位移量,Sx0、Sy0、Sz0为动栅与静栅的初始相对面积,L为静栅边长。分别对三通道使用此位移模型,并做变形以适应线性回归系统
(6)
2.2 系统误差分析
一般情况下,容栅传感器的电场在栅极边缘处不能均匀分布,产生边缘效应,是传感器设计过程中必须要考虑的因素。边缘效应导致传感器灵敏度下降和电容值非线性增加,实际电容值在理论电容值基础上加上附加电容值,即:C实际=C理论+C边缘。
C边缘不是一个常量,其与栅极数量、栅极厚度、栅极间距均有关联,且在传感器信号动态变化时尤为严重[6]。在加工工艺、成本制造等各方面因素影响下,尽可能减小极板间距和极板厚度、控制栅极对数并适当增大初始电容C0,使边缘效应造成的影响最小[7]。
2.3 M估计线性回归算法
2.3.1 M估计背景
M估计(maximum likelihood type estimation,M-Estimation)是一种迭代加权最小二乘法,属于稳健回归的一种[8],由Huber于1964年提出,也被称为广义最大似然估计,其原理是给每个样本点不同的权重,偏差较大的样本点权重小,偏差较小的样本点权重大,异常点出现时不会对拟合方程产生较大影响。
2.3.2 M估计运算准则
M估计的运算方法有很多,而迭代加权法(iteratively reweighted least squares,IRLS)由于其算法类似于最小二乘法,易于编写和移植,故而得到广泛的应用。
对于有i个影响因素的自变量矩阵X=[x1,x2,…,xi],其与因变量Y的关系如下
Y=β1x1+β2x2+…+βixi+b
(7)
最小二乘法的残差函数为
(8)
运算准则为
(9)
M估计采用迭代加权最小二乘回归系数,根据前一次回归残差确定各样本权重,残差函数被改写为
(10)
则M估计的运算准则为
(11)
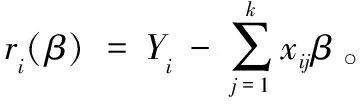
ρ为影响函数,一般满足以下条件[9]:
(1)ρ(r)≥0;
(2)ρ(0)=0;
(3)ρ(-r)=ρ(r);
(4)If|ri|≥|rj|,thenρ(ri)≥ρ(rj)。
为了保证M估计的回归系数通因变量的观测单位无关,希望M估计结果具有尺度同变形,即满足
(12)
为满足上式条件,估计回归系数β需将残差ri标准化,除以某个尺度参数σ,得到标准化残差ri/σ。
M估计的运算准则即定义为如下
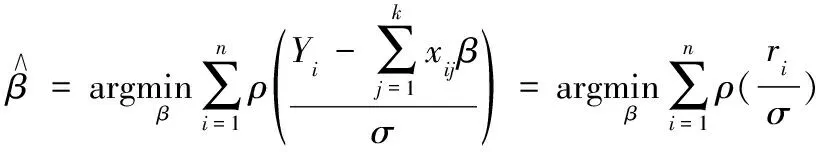
(13)
实际运算中,Hampel于1974年提出以ri(β)观察点的绝对离差中位数(median absolute deviation,MAD),除以常数0.6745作为稳健估计尺度σ[10]。
MAD是一种衡量数据离散分布的鲁棒性测量方法,同时也可表示样本的总体参数。对于单变量数据集M=[M1,M2,…Mn],其MAD公式为
MAD=median(|Mi-median(M)|)
(14)
2.3.3 常用的影响函数
在稳健估计中,有几种常用的影响函数,以及对应的导函数和权因子:
(1)最小二乘法
最小二乘法是一种特殊的M估计
Ψ(u)=u
(2)绝对和极小法(LAD估计)
ρ(u)=|u|
Ψ(u)=sign(u)
LAD估计又称L1估计,是Lp估计的一种,p值越小,β收敛到最小值需要的迭代次数越多,是一种较为准确但收敛较慢的影响函数。
(3)Huber法
本文选用Huber loss[11,12],降低了对离群点的惩罚程度,适合数据接近正态分布的情况,是一种具有良好鲁棒性的影响函数。
Huber提出一种加权函数[11-13]
|u|≤c

|u|≥c
Ψ(u)=u
|u|≤c
=c·sign(u)
|u|≥c
其中,c是常数,通常默认为1.345,为Huber的尺度参数。Huber算法可以看作将最小二乘法和LAD法相结合。当残差绝对值较小处,使用最小二乘法;残差绝对值大处使用LAD。这种估值方法既能提高系统的准确性,也有较高的估值效率。
Huber函数在不同尺度下的function如图4所示。
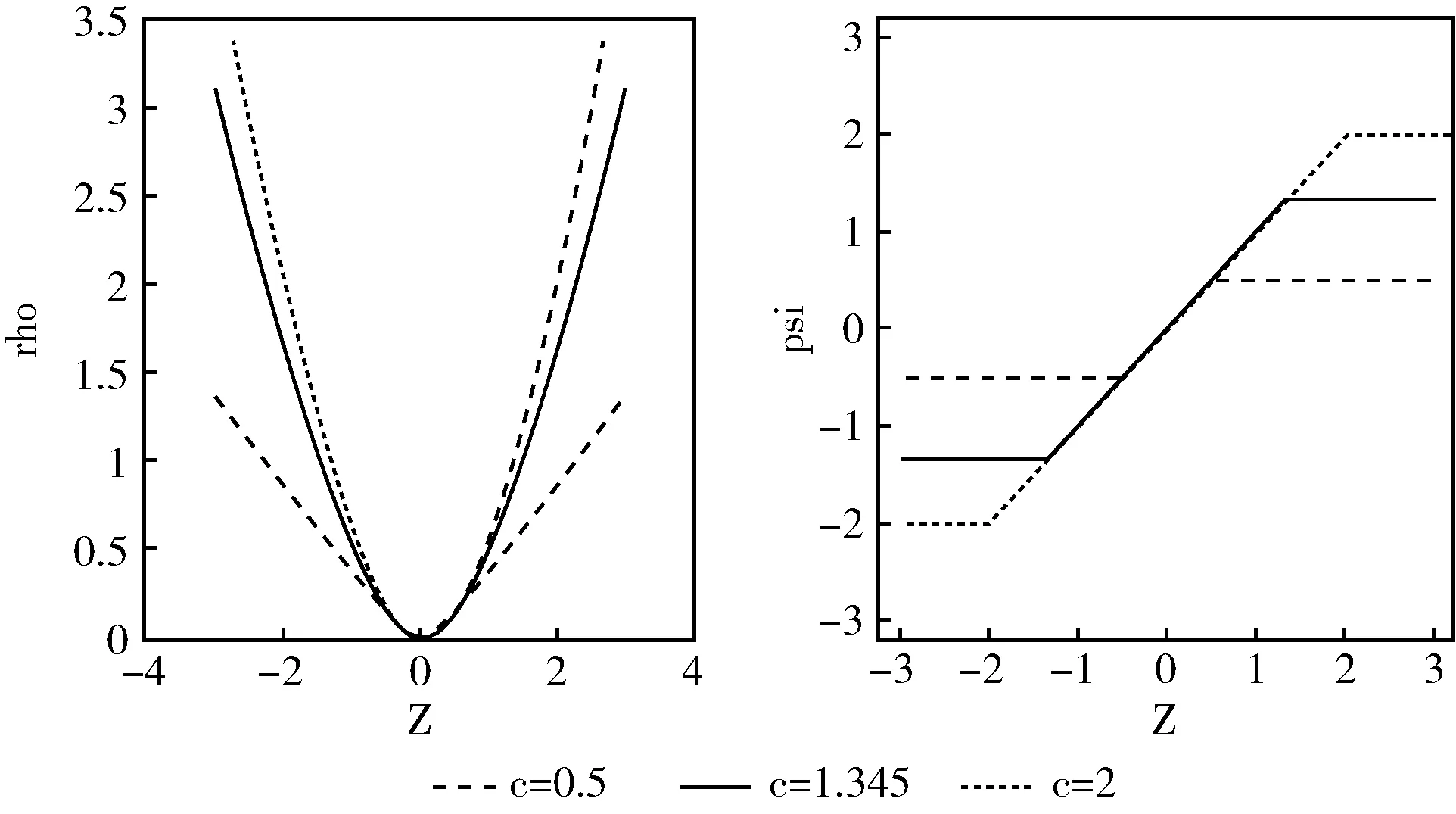
图4 Huber function 原函数和导函数图像
2.3.4 M估计具体算法
对残差函数的表达形式预处理:
(1)式(10)中目标函数ρ(ri)对β求偏导得
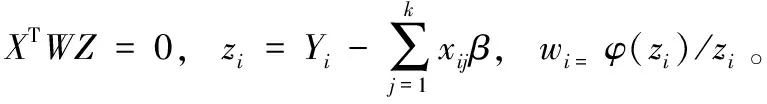
(2)对线性方程组向量化得XTWe=0
(3)将Y=Xβ+e代入得XTWXβ=XTWY
(4)得β=(XTWX)-1XTWY
具体算法步骤为:
(1)建立U=xβ+b的线性方程组,根据OLS求出初始残差e0;
(2)标准化残差得到zi,由wi=φ(zi)/zi作为样本的初始权重;
(3)又由β=(XTWX)-1XTWY求出新的β(i)以求得新的残差代替β(i-1);
(4)返回(2)进行迭代依次计算β(i),给定残差迭代阈值ξ,当|β(k+1)-β(k)|<ξ,此时满足收敛条件,βM=β(k+1)。
2.3.5 M估计对测试系统的作用
在本系统设计中,M估计主要作用是在系统标定完成后,实际测试时预测系统参数。微小位移系统安装时,由于同心球内空间狭小,一旦安装完成很难调整容栅传感器栅极相对位置,M估计可以及时比较测量值和预测值的残差,对系统的安装调试具有显著意义。
2.3.6 皮尔逊相关性分析
为了分析OLS和M估计的拟合优度,采用卡尔皮尔逊提出的皮尔逊相关系数法(Person correlation coefficient),又称皮尔逊积矩相关系数,是一种准确度量两个变量之间关系密切程度的统计学方法[14]。
一般情况下,皮尔逊相关具有如下约束条件:
(1)两个变量间有线性关系;
(2)变量为连续变量;
(3)变量均近似符合正态分布,且二元分布也符合正态分布;
(4)两个变量均为独立变量。
对于两组变量X,Y,通过实验得到若干组数据对,记为(xi,yi)(i=1,2,…,n),样本的总体相关系数数学表达式为
(15)
估算样本的协方差和标准差,则皮尔逊相关系数表达式为
(16)
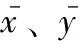

表1 皮尔逊相关系数的关联程度
样本相关系数是通过样本数据计算得到,其值受到样本的随机性、数量等影响。因此需要对样本相关系数做显著性检验,即求P-value。Z检验一般用于大样本均值差异性检验的方法,不太适合本测试。T分布检验是一种小样本分布检验,较为适合本测试,构造一个统计量t,构造方式如下
(17)
这个统计量是符合自由度为t-2的T分布。其中n为样本的数量,r是皮尔逊相关系数ρX,Y。
定义原假设H0为r等于0,即不存在线性相关性,通过T分布表得出满足拒绝H0的显著性水平α,显著性检验是“小概率事件实际不可能原理”,α越接近于0,越说明原假设不成立,数据具有统计学意义。
3 实验测试和数据分析
3.1 正态性分析
线性回归参数估计要求被测数据集满足或近似满足正态分布。考虑到测试数据正可能不具有良好正态性,有以下几种处理手段:
(1)若方差正比于均值,进行平方根转换;
(2)若标准差正比于均值,进行对数转换;
(3)还可以采用Yeo-Johnson或Box-Cox变换,这是针对随机变量正态性较差时做的数据预处理。当预处理后的数据偏离原始数据的性质时,可认为该数据不适用正态性校验方法,转而采用非参数检验方法如秩和检验、中位数评分检验等。
位移数据由系统模型搭建完成后采样得到,利用SPSS Statistics数据分析软件对3个通道所得数据使用直方图和P-P图两种统计学方法进行正态性分析[15],验证结果如图5所示,可知XYZ三通道采样数据具有较良好的正态性。
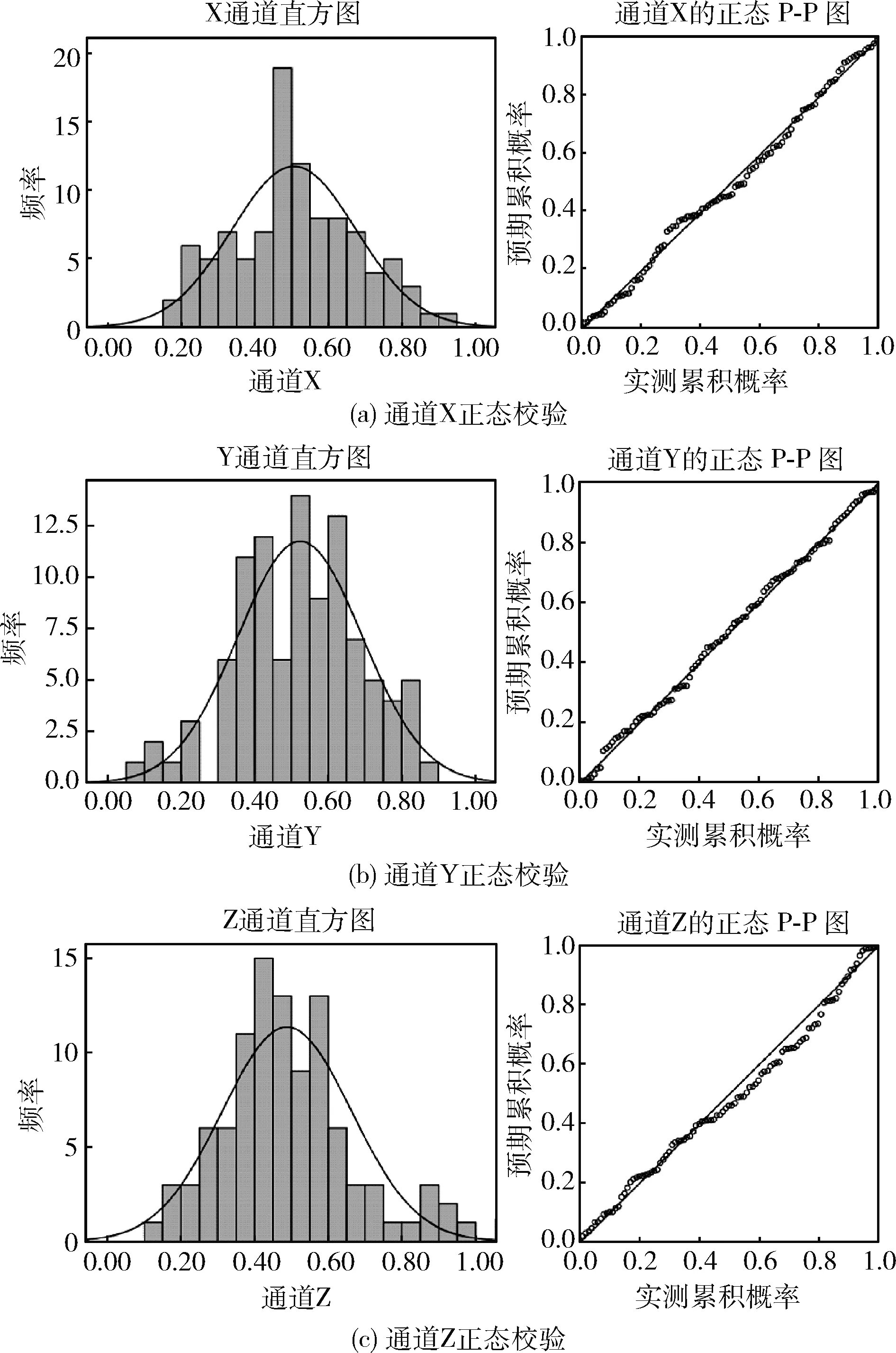
图5 三通道正态性校验
3.2 数据标定与分析
图6为此系统的标定装置,其作用是:①检测容栅传感器性能参数是否符合预定标准以及理论模型是否正确;②提供一个标定值(认定是真值)。

图6 标定测试装置
测试时,通过调节标定平台上的千分尺旋钮精确控制动栅和静栅之间的距离,此装置最小分辨率为0.01 mm,虽精度没有达到0.001 mm,但可估读到0.001 mm,满足电路调试和数据标定0.05 mm步长的要求。
选定0.3 mm~0.95 mm为标定距离范围,0.05 mm为步长,由于电压倒数只是统计学上方便计算的操作,无实际的物理意义,也没有对应的物理单位,所以还是使用电压单位V,得到如表2所示的关系表。
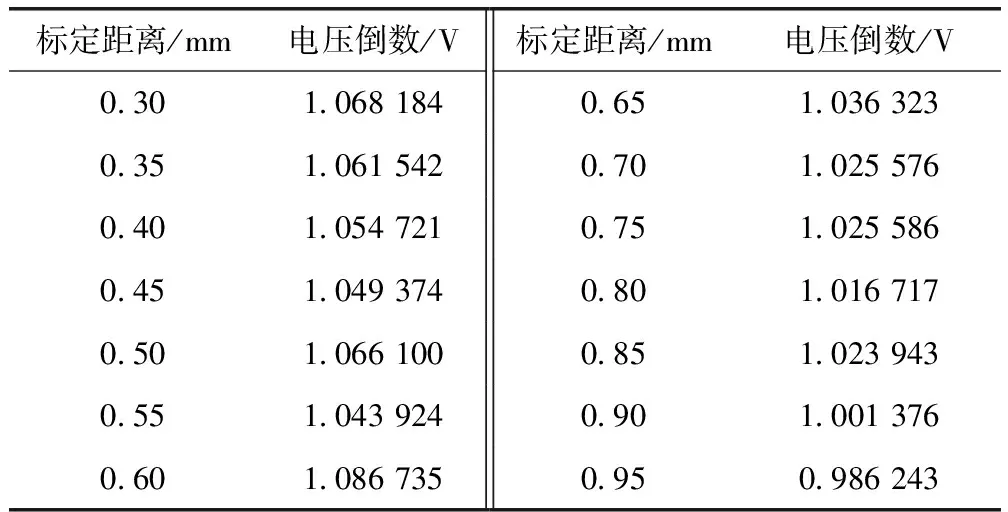
表2 标定距离和采集电压倒数
对标定距离x和采集电压的倒数1/UX使用Matlab软件做OLS和M估计线性回归参数估计,标定了14组数据,其拟合效果如图7所示。
据图7可知,拟合直线对于偏差过大的离散点敏感性降低,避免了标定过程中因操作失误等因素造成系统拟合直线偏移。
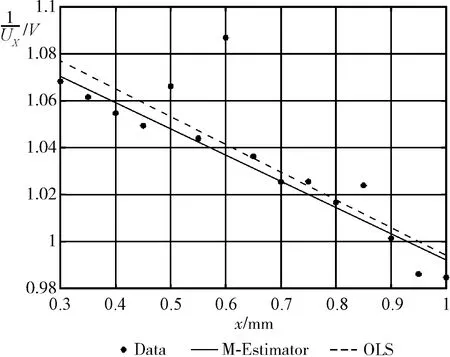
图7 X通道电压倒数与位移关系
使用此算法分别得到3个通道M估计预测线性回归方程为
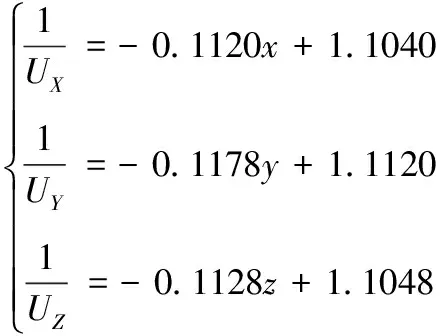
(18)
模型搭建完成后,在标定平台上对系统标定,验证测试距离与标定距离的相对误差,同时对比OLS预测距离和M估计预测距离相较于测试距离的相对残差,分析两种算法的优劣。
表3、表4、表5为标定平台三通道测量数据,Z通道在测量0.40 mm这一组数据时,出现了明显的离群值,经检查,认为是标定时出现误触导致装置的偏移,容栅传感器相对面积发生变化造成测量的不准确,经重新多次测量得数据为0.398 mm。三通道相对误差符合预期值,相对误差均小于3%。分别计算两种算法相较测试距离的相对残差:(测量值-预测值)/测量值×100%,在(0.30 mm,0.40 mm),虽然OLS预测距离比M估计距离和实测距离都要更接近标定距离,但算法预测主要作用是校准传感器,而不是预测真值,评价其拟合优度指标是相对残差,且在(0.40 mm,0.60 mm),OLS预测距离逐渐偏离真值,综合三通道算法预测表现,M估计总体优于OLS,具有良好的拟合效果和鲁棒性。
将表3、表4、表5中OLS与M估计预测结果分别进行皮尔逊相关性分析,汇总结果见表6。
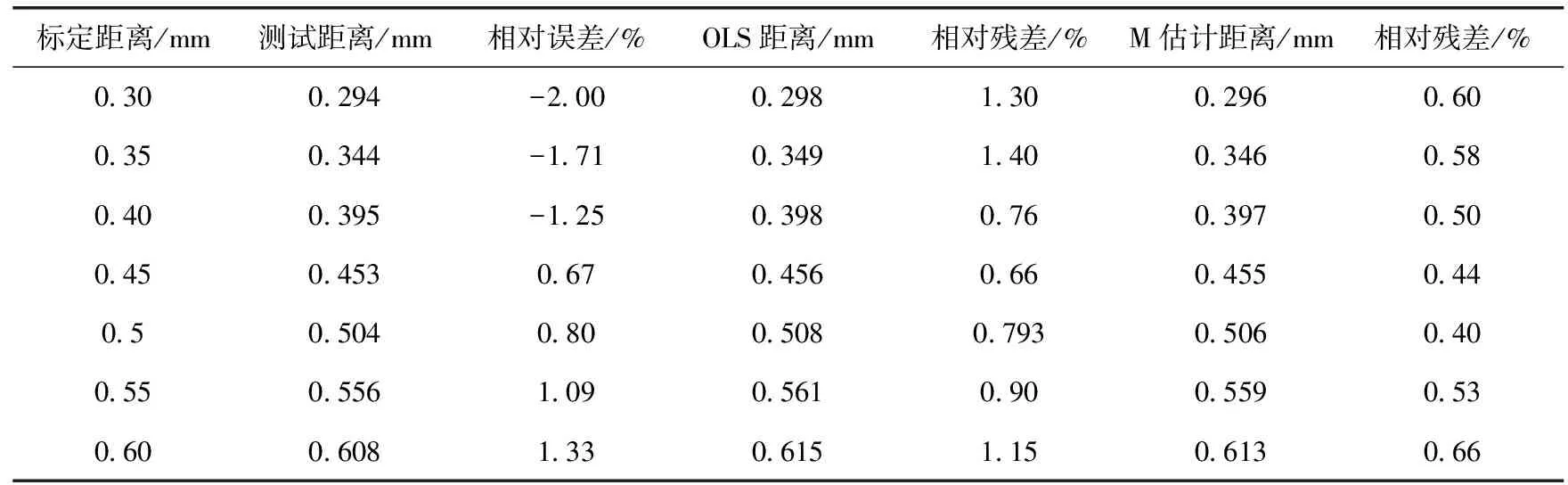
表3 X通道测试距离、预测距离相对残差
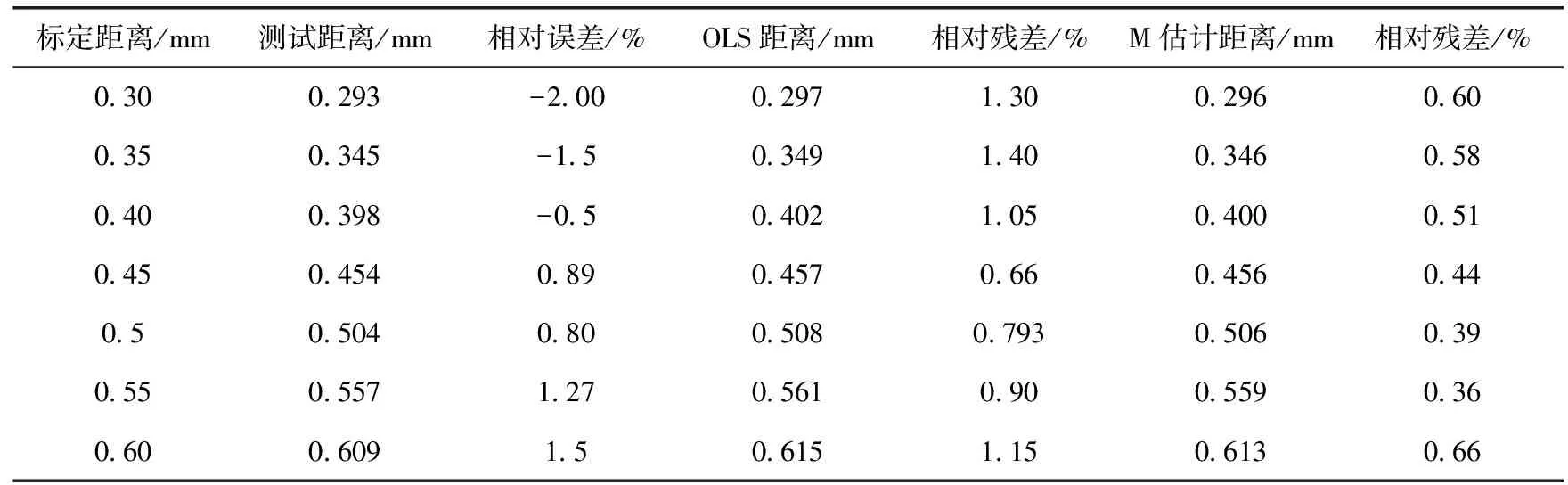
表4 Y通道测试距离、预测距离相对残差
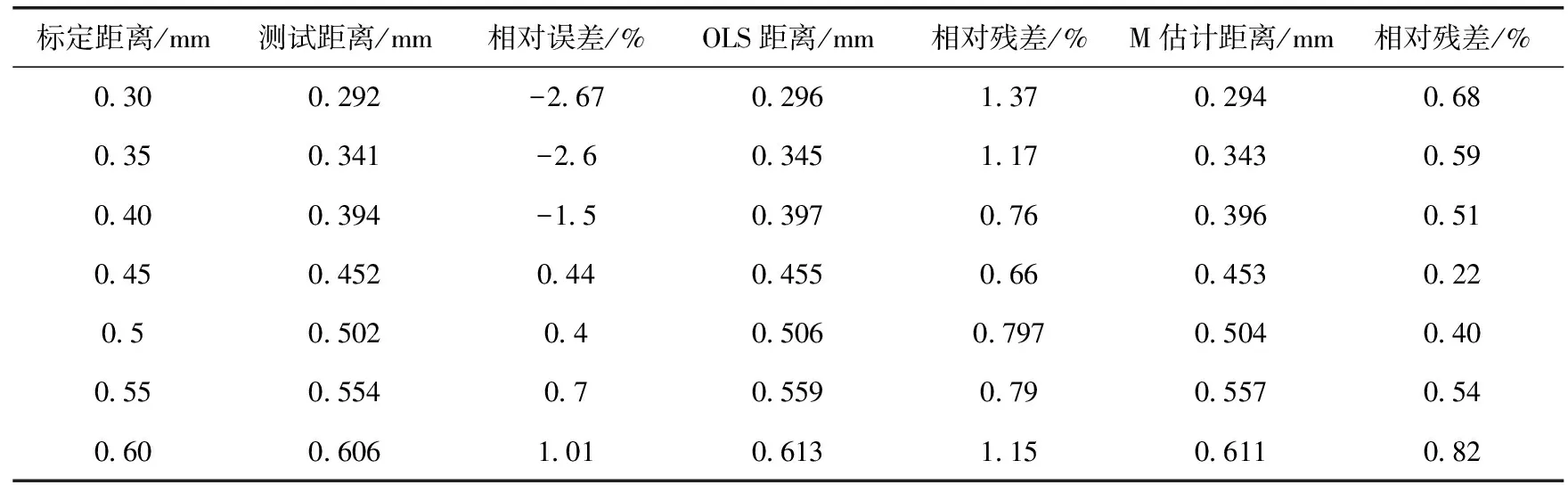
表5 Z通道测试距离、预测距离相对残差

表6 相关性和显著性分析
由表6可知,经皮尔逊相关性分析,两种算法预测值均与测量值显著线性正相关且M估计相关性和显著性均优于OLS。
4 结束语
本文针对三维容栅微小位移测试系统,根据先验经验,使用直方图和P-P图法对测量数据做正态性检验,确保模型为线性系统;提出了使用M估计的方法,克服了普通最小二乘法对离群点的敏感性,避免了因操作不当对系统拟合产生不利影响。皮尔逊相关性分析验证了M估计预测值与测量值具有相关性和显著性。经实验测试,该算法提高了预测模型的可靠性,可应用于同心球内狭小空间的三维容栅微小位移系统安装校准。
不足之处为该模型将传感器视为平板电容,所以只能建立在较大曲率半径的同心球上以求计算时可以忽略传感器的曲率。对较小球体的微小位移测量仍需改进模型,使其适应更多的球体系统。
