基于改进谱聚类算法的交通区域划分方法

杨 迪，蔡怡然，王 鹏，李岩芳

(长春理工大学 计算机科学技术学院，吉林 长春 130022)

0 引 言

交通拥堵是目前全世界共同面临又亟待解决的问题，其态势一般存在区域性和不确定性。合理高效的交通区域划分能够清晰地展现交通传播规律以及区域道路拥堵情况，对于交通疏导具有实际的指导意义。目前学者们对于路网动态划分问题进行了广泛的研究。路网动态划分方法主要有传统划分方法，如基于多特征参数的划分方法[1-5]、基于MFD属性划分方法[6]和智能划分方法，如基于遗传算法的划分方法[7]、基于谱聚类算法的划分方法[8-12]。由于谱聚类算法[13]操作简单，具有较强的普适性，被广泛应用于路网划分中，但算法本身相似图的计算会忽视路网节点之间复杂的关联性，而且易产生局部最优解等问题。针对这些问题有不少改进方案被提出，如Yang等[8]提出了一种异构时空交通三阶段模式的路网划分方法，将路网划分为相似性较高的区域子网。赵菲等[11]提出了基于边聚类系数的谱聚类子区划分方法，改善图谱划分的局限性。Tarique等[12]提出了基于密度聚类和谱聚类的路网划分方法，提高路网划分聚类精度。

虽然上述改进提升了谱聚类的部分性能，但是大部分方法所承载的路网结构信息较少，并且没有结合实际交通路网环境。本文结合实际路网交通环境提出了一种基于改进谱聚类算法的交通区域划分方法，其利用马尔可夫链完善谱聚类算法的相似图，通过转移概率重新构造路网节点之间的相似图，确保能够反映出完整的路网信息，同时针对聚类初始中心节点敏感的问题，通过遗传算法，提高谱聚类的全局搜索能力，保证路网分区的准确度。

1 基于谱聚类算法的区域划分算法

谱聚类是基于图论的聚类算法，其原理是将原本的聚类问题转化为拓扑图的划分问题。利用节点之间相似度设计相似矩阵，计算出该矩阵的前k特征向量,从而将不同数据点进行分类。

谱聚类算法应用于交通路网步骤如下：

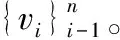
E={(vi,vj)|(vi,vj)∈V×V,vivj}

(1)

步骤2 构造相似矩阵W。使用一个非负的相似矩阵W表示整个无向图，其元素wij表示无向图中的两个节点vi和vj之间的权重，并且wij=wji。然后得出相似矩阵W，相似矩阵W的计算表达式为式(2)

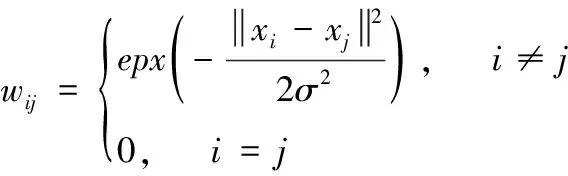
(2)

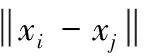
步骤3 计算拉普拉斯矩阵L=D-W。D为度矩阵，其计算表达式为式(3)

(3)

式中：元素wij表示无向图中的两个节点vi和vj之间的权重。

步骤4 构建标准化后拉式矩阵D-1/2LD-1/2。

步骤5 求标准化后拉式矩阵的前k个最大特征值以及相应的特征向量(ξ1ξ2…ξk)，得到特征向量矩阵X。

步骤6 计算矩阵X的行向量，得到矩阵Y，其计算表达式为式(4)

(4)

式中：Xij表示第i行第j列元素。

步骤7 将Y的每一行作为Rc空间的一个样本，使用k-means聚类，得到k个聚类。

步骤8 如果Y的第i行在j类中，那么当且仅当Y的第i行被归为聚类j中。

2 改进谱聚类的区域划分方法

2.1 基于加权相似图的路网提取方法

路网中相邻路段间具有更紧密更复杂的结构关系，传统谱聚类的相似图是基于欧式距离得出，其计算简单，但是容易忽略隐性的路网结构信息。路网中节点之间的关系会随空间距离的增加而减弱，在交通流量的传播作用下，路网间交通流量的关联度也会随路网空间距离的增加而不断地减小。通过路网间的转移概率反映出交通流量随着距离变化的趋势，从而进一步模拟出完整的路网关系相似图。而以往的谱聚类相似图仅考虑了相邻路段间的关系，忽略了在传播作用下，路网间交通流量的转移关系，应用于路网中难以有效反映路网的关联度，使得聚类效果不理想，本节通过马尔可夫链的转移概率构建谱聚类的相似图。

2.1.1 转移概率和概率矩阵

马尔科夫链是一个状态转移到另一个状态的随机转换过程，空间状态之间变换的概率叫作转移概率，并且未来状态只依赖于当前状态。交通路网随时间空间变化存在复杂的状态转移关系，其中交通流量每一时刻所在路网节点为状态空间，而下一时刻所在路网节点状态仅与车流量此时所在节点状态有关。通过节点之间马尔可夫的转移概率来模拟复杂的路网关系，计算谱聚类相似度，并且重新构造相似图。

给定路网G，令t时刻路网流量状态为随机变量，利用概率矩阵表达路网节点之间的状态转移概率，根据马尔科夫链特征并且满足以下性质，其计算表达式为式(5)

P{X(t+1)=at+1|X(t)=at,…,X(1)=a1}=

P{X(t+1)=at+1|X(t)=at}

(5)

式中：X(t)为t时刻的马尔科夫过程，A={a1,a2,…,at} 为路网状态空间。

通过交通流量特征，计算t时刻节点状态到下一时刻节点状态的转移概率Pij，其计算表达式为式(6)

(6)

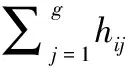
由此构建构成路网的转移概率矩阵P，其计算表达式为式(7)

(7)

路网中状态之间的状态转移过程如图1所示。

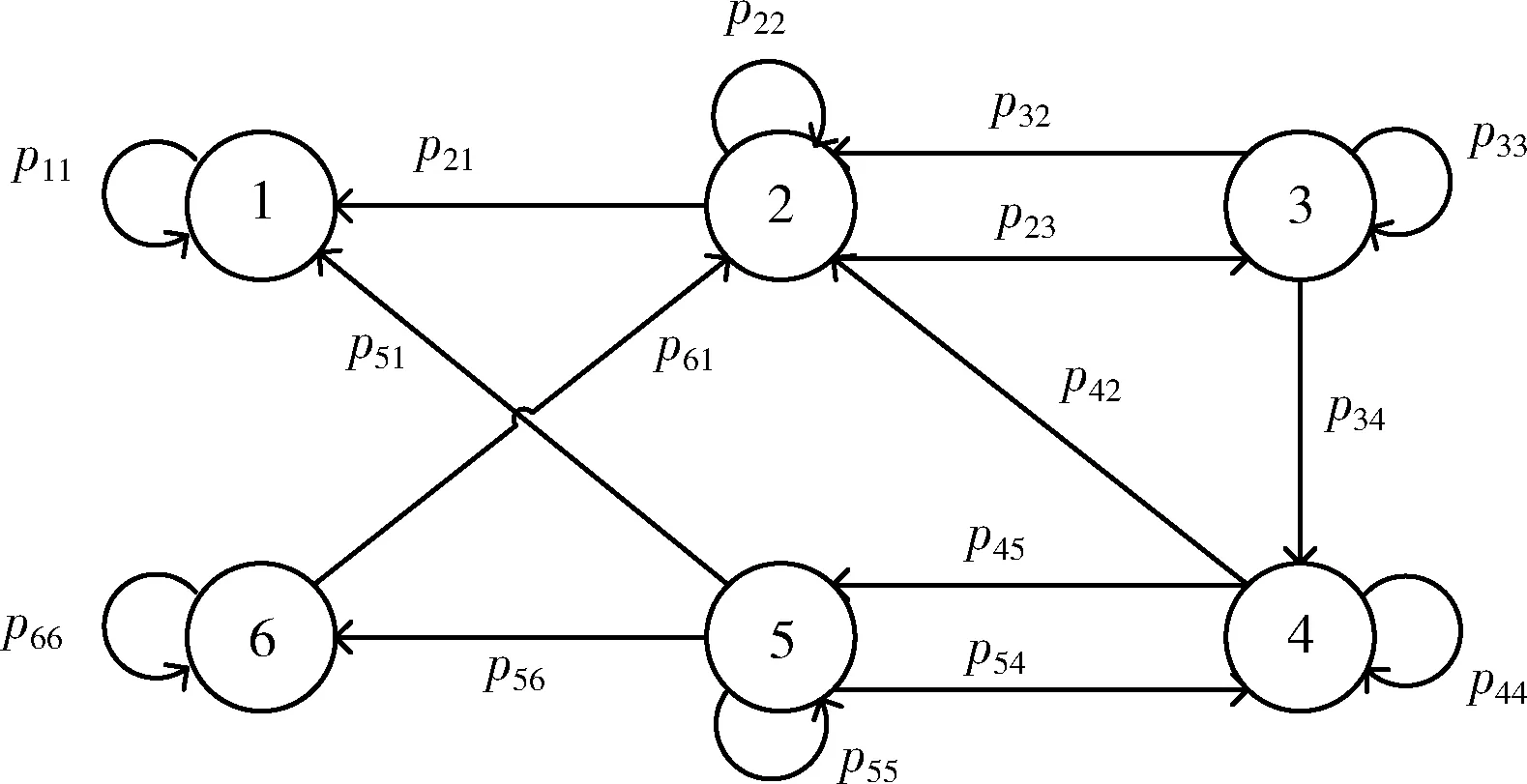
图1 路网状态转移过程

其中，节点表达路网状态空间，pij为路网的转移概率。例如p21为路网流量状态2转移到状态1的概率。同时，在路网空间状态中处于状态2的路网流量下一刻选择的空间状态的概率都取决于路网流量当前所处的状态。

转移概率矩阵P中的状态转移仅依赖于前一个状态，其能够直观地描述节点与相邻节点之间的路网关系，但是无法描述与多个非邻近路网区域节点之间关系。通过多次状态转移得到高阶转移概率，可以拓展更多非邻近节点，所以利用高阶转移概率来表征交通区域各个节点之间存在的复杂路网关系。

给定路网G，路网空间状态个数为g，通过计算路网交通流量的转移概率矩阵，其所得到的特征向量作为路网交通流量权重即马尔科夫的状态向量为R，R={r1,r2,…,rg}。路网节点i状态到达节点j状态期间经过m次转移，则状态的转变仅依赖于前m个状态，得到m阶转移概率矩阵Pm，其计算表达式为式(8)

Pm=rmpm

(8)

式中：rm为m阶转移概率的权值,pm为m阶矩阵。

进而构建马尔可夫模型，其计算表达式为式(9)

X(t+m)=PmX(t)

(9)

式中：马尔可夫链模型的初值为X(1)。

2.1.2 相似图的计算

给定路网G，m阶转移概率矩阵为Pm，通过概率矩阵Pm构建相似矩阵W，路网中节点i和j之间相似度wij，其计算表达式为式(10)

(10)

式中：pmij是节点i处状态转移到节点j的概率。

通过相似矩阵W所构建的拉普拉斯矩阵满足以下性质：

(1)L=D-W，其中D为度矩阵，所有的特征值都是实数。

(2)对于任意向量f，都满足计算表达式(11)

fTLf=fTDf-fTWf=

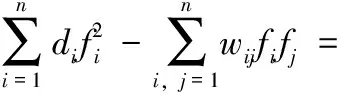
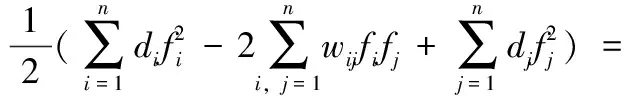
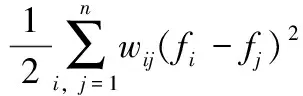
(11)

表明W能够构造Laplace矩阵，进而得出谱聚类算法的相似图。基于以上推导，基于转移概率矩阵实现了谱聚类相似图构造。

2.2 基于遗传算法的谱聚类优化方法

传统谱聚类中k-means算法对初始中心十分敏感，聚类中心的选择直接影响聚类结果的准确性，而不恰当的聚类中心往往会造成路网划分区域间差异大，相邻子区间的划分作用不明显，导致路网划分效果不理想。本节为了提高路网的全局寻优能力，利用GA聚类算法对特征向量进行优化，其应用于谱聚类最后一步聚。

2.2.1 个体编码与种群初始化

本文采用浮点数编码的方式生成交通路网的初始种群，给定的路网聚类数量k，将通过拉普拉斯矩阵计算得出的特征向量设为初始样本集Q，路网两个节点之间的流量相似度设为基因，将路网随机划分成各个子区域。

2.2.2 适应度函数

遗传算法的收敛速度以及能否找到最优解与遗传算法适应函数的选取有关。本文构造适应度函数f通过路网中每个节点的特征来判断路网各个节点的适应度，其计算表达式为式(12)

(12)

式中：b为常数，E为样本集的误差平方和。

2.2.3 遗传聚类操作

本文选取轮盘赌选择方法，路网中每个节点能否进入下一代由其相对适应度所决定。然后进行交叉，路网中两个节点随机地交换基因，交叉后若发现子代具有相同点则归并相同点，若没有，则确定父辈是否在路网中有对应基因的权值不为零，即有直接的路网关系。若有，则选取子代中最优的基因对进行交叉操作。交叉操作可以完善算法在路网中的全局搜索能力，变异操作则保障了其局部搜索能力，防止过早收敛。

经过以上操作后，路网每次都需要重新计算各特征向量与各路网节点之间复杂的权重的关系，重新划分种群，经过迭代后适应度最大的路网节点为最终结果。最后，按照与最终结果空间关系最近原则重新聚类划分样本集，得到路网聚类划分结果。

2.3 算法总体框架

针对谱聚类中基于欧式距离计算的相似图无法表征路网隐含信息的问题以及聚类初始化中心敏感的问题，本文提出的改进谱聚类的区域划分方法(ISC)。首先，根据实际路网构建路网拓扑图G=(V,E)。其次，通过构建马尔可夫链转移概率矩阵方法，利用路网节点之间的关联权重来表征出完整的路网信息，重新构造相似矩阵W。然后，计算拉普拉斯矩阵，得出拉普拉斯矩阵L前k个最大特征值以及相应的特征向量。最后构造空间特征样本集，通过遗传优化选取全局最优的聚类中心进行聚类，得出聚类结果进行路网划分。算法步骤如图2所示。

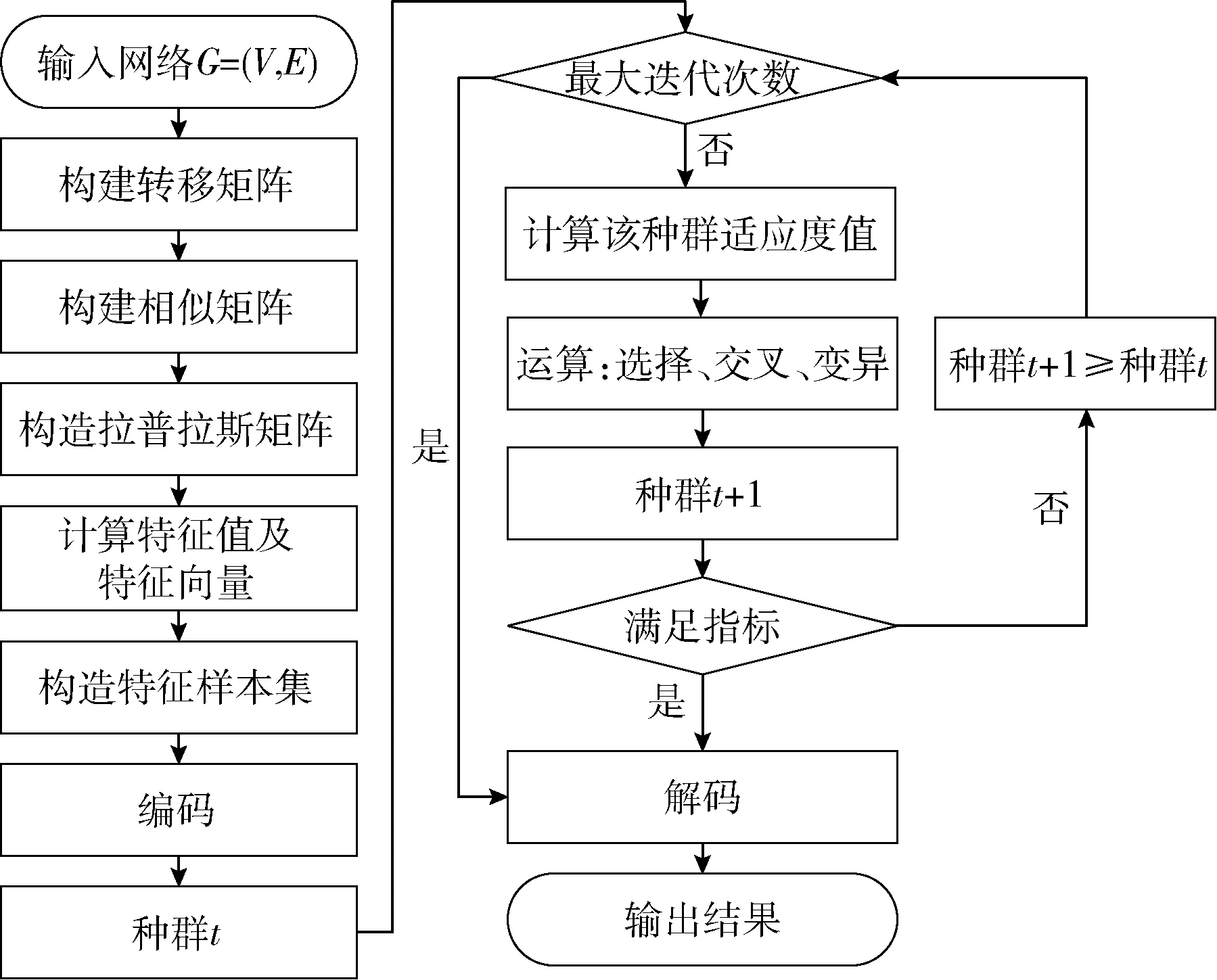
图2 算法总体步骤

算法流程：

输入：网络G=(V,E)

输出：路网划分结果

(1)计算转移概率矩阵Pm。

(2)构建相似矩阵W。

(3)构造拉普拉斯矩阵L，L=D-W。

(4)将L特征分解，计算最小的特征值以及对应特征向量。

(5)将对应节点映射至k维空间，作为特征样本集。

(6)将样本集进行编码并生成初始种群。

(7)计算初始种群的适应度函数并设置迭代次数。

(8)结合传统遗传算法对第i代的种群进行遗传操作得到新一代的种群。

(9)判定迭代次数是否为迭代次数最大值，如果是，则i=i+1，回到(8)，否则结束迭代过程，将种群中适应度函数最大的个体作为算法的最后结果。

(10)根据最后结果进行划分路网。

3 实验分析

以四川省成都市市中心作为研究对象，研究区域从西城大街东到东城根大街，北起人民中路至人民东路，共计23个路段交叉点，32条路段，根据实际道路路网和道路GPS数据可以得到路网的拓扑结构图G=(V,E)，拓扑图如图3所示。

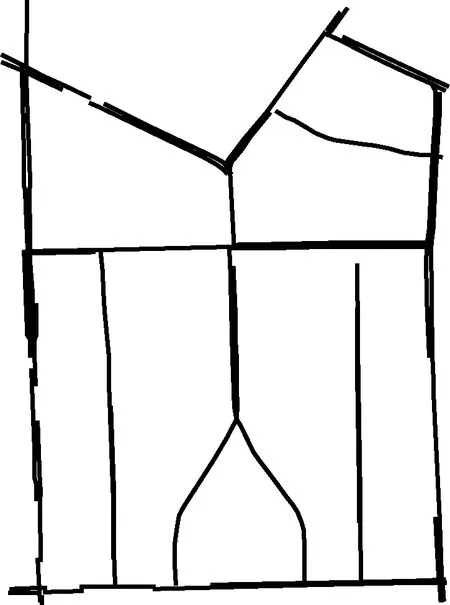
图3 研究区域范围拓扑

选取2014年8月3日成都1.4万辆出租车GPS轨迹数据，利用ArcGIS通过地理坐标将GPS轨迹数据与实际道路路网匹配。不同时段交通流量密度变化如图4～图6所示：早上8:00至8:15和晚上18:00至18:15处于早高峰时段和晚高峰时段，各路段车流量较大，交通流量比较密集，中午12:00至12:15处于平峰时期流量较高峰时相对减少。

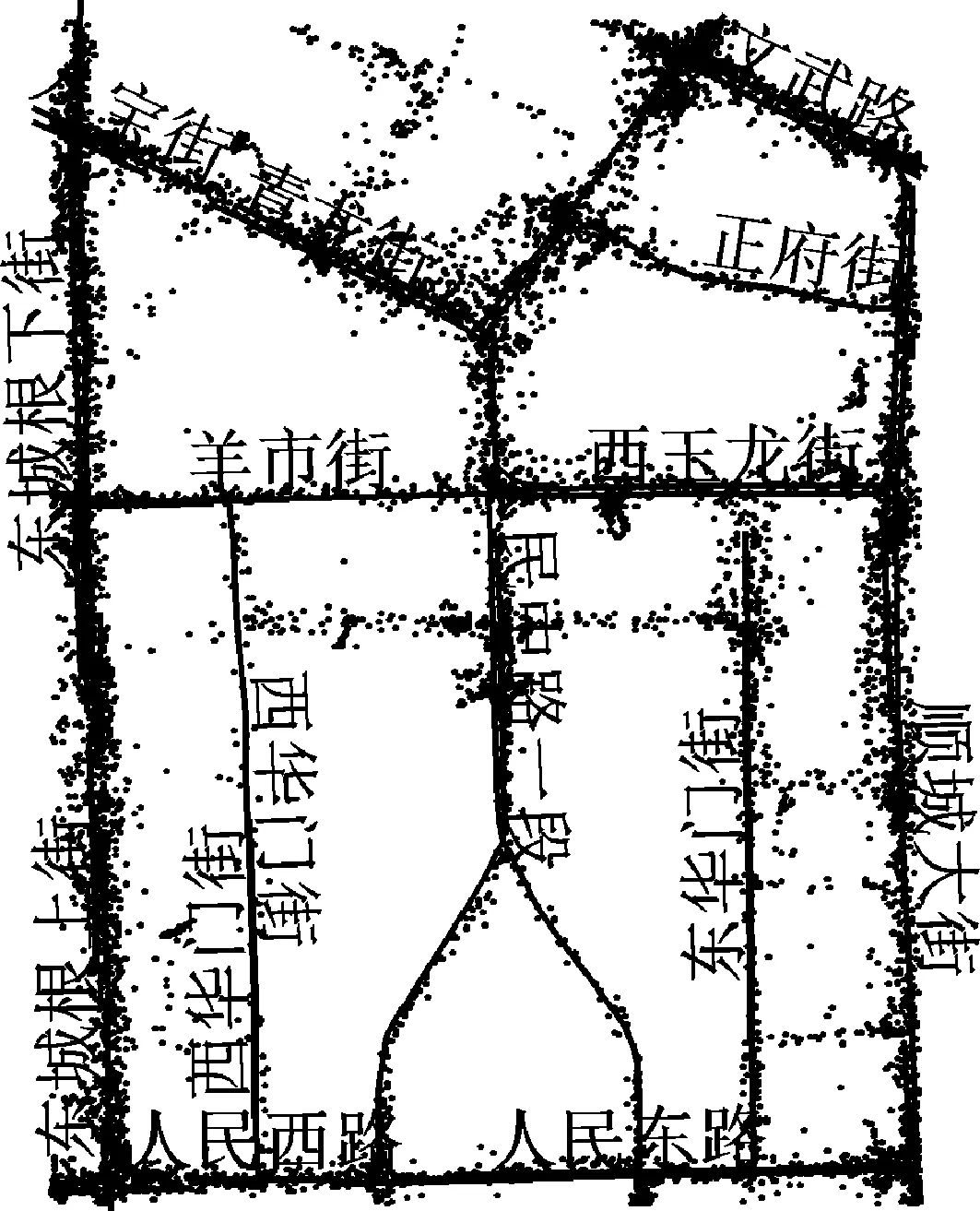
图4 早上8:00-8:15时段出租车GPS数据分布

图5 中午12:00-12:15时段出租车GPS数据分布

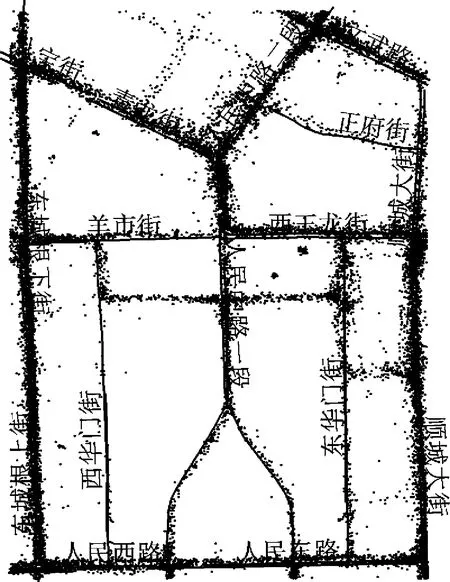
图6 晚上18:00-18:15时段出租车GPS数据分布

3.1 分区评价指标

路网子区域划分结果应该满足区域内部的同质性和相邻子区间的差异性，因此利用归一化总体方差方法(TVn)来评估本文算法的区域内部的同质性，NCut Silhouette(NSk)来表征本文算法的相邻子区间的差异性，从而判断其路网划分结果的合理性和科学性。

归一化总体方差(TVn)为各子区域内部速度方差的和与整个路网速度方差的比值。对于k个子区域的分区结果，归一化总体方差计算表达式为式(13)

(13)

式中：R为路网的道路集合，NRi为子区Ri内的道路数目，N为路网道路总数。Vart(Ri)为Ri在t时速度的方差，t为时间序列长度。TVn主要评判路网划分后各个子区内部路段的相似性。当划分子区越多，子区内部路段越少，路段相似度越高，则该评价指标越小。

NCut Silhouette(NSk)[14]评估不同子区的路段间在各个时刻t的速度差平方的平均值。对于整体路网划分结果的总体评价计算表达式为式(14)

(14)

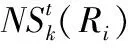
3.2 路网子区划分

本文从实际应用方面考虑，路网子区的划分数量过多不利于交通管控，使得管理计算成本过高，结合所研究的路网分布，为获取较好的分区效果，将所研究的路网划分为6个子区。实际交通路网中早高峰时期交通流量变化大，流量密度较集中，能够显现出更多交通流量特征，故选取2014年8月3日早上8:00-8:15时早高峰的实际路网交通流数据作为研究对象，通过将具有相似特征的流量进行聚类实现路网划分。根据参考文献[15]的参数设置并结合多次实验结果，实验所需相关参数设定见表1。

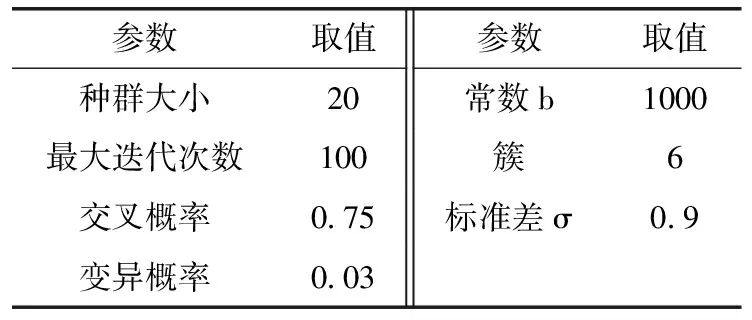
表1 实验所需相关参数设定

将本文算法(ISC)与传统谱聚类算法(SC)、基于马尔可夫的谱聚类算法(MKSC)、基于遗传算法的谱聚类算法(GASC)的划分结果在相同的实验环境下进行有效性对比，实验参数设置见表2，子区划分评价结果如表2、图7所示。

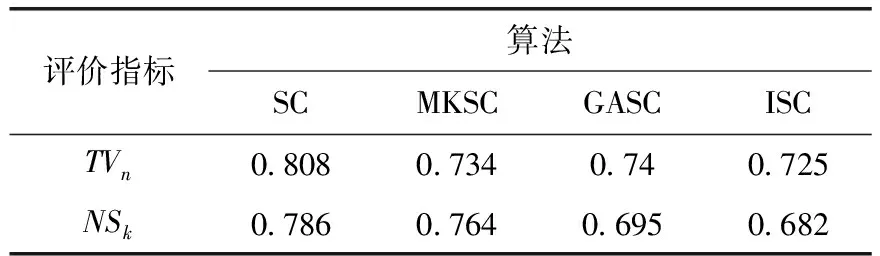
表2 路网划分评价结果

图7 路网划分评价指标

从表2可以看出MKSC算法与传统SC算法相比TVn评价指标降低了9.16%，NSk指标降低了2.8%，表明了MKSC算法相比于欧氏距离构造相似矩阵的SC算法容易忽视路网之间复杂的关联关系，考虑了交通路网之间的流量传播规律，通过转移概率模拟路网节点间流量变化以构造反映交通区域结构的谱聚类相似图，从而减少了由于空间距离的增加对路网节点之间交通关系的影响，增强了相似图的健壮性，提高了聚类效果。GASC算法与传统SC算法相比TVn评价指标降低了8.42%，NSk指标降低了11.58%，表明了GASC算法通过对特征向量选取过程进行优化，结合遗传进化思想对全局聚类中心寻优完成聚类，能够克服传统谱聚类对初始值选取较敏感的问题，提高了路网全局搜索能力，提升了聚类精度。本文所提出的ISC算法在两个指标上取得了最小值，其子区划分效果优于SC、MKSC、GASC这3个算法，在TVn指标上分别降低了10.27%、1.23%、2.03%，在NSk指标上分别降低了13.23%、10.73%、1.87%，表明了本文所提出的ISC算法具备高内聚低耦合的特性。基准算法SC、GASC算法忽略了在传播作用下路网间交通流量的转移关系，通过欧式距离得出的相似矩阵难以有效表征路网信息。SC、MKSC算法对于聚类初始中心选择的较为敏感，容易产生局部最优解，不利于算法运行。ISC算法相较于其它算法，同时考虑了欧氏距离的不合理性和聚类中心的敏感性，采用马尔科夫的转移概率重构相似图，同时通过遗传算法优化聚类中心，使交通子区更符合实际路网情况，提高模型整体聚类效果。由图7可以看出本文算法与其它算法相比TVn评价指标和NSk评价指标相对较低，表明了本文算法既使得各个子区内部具有较高的相似性同时又能保证路网子区之间的差异性，在路网划分中比较有优势，更加符合实际交通特性，验证了本文算法的有效性。

本文所提出的算法(ISC)与传统谱聚类算法(SC)、基于马尔可夫的谱聚类算法(MKSC)、基于遗传算法的谱聚类算法(GASC)对应路网划分结果如图8(a)～图8(d)所示。

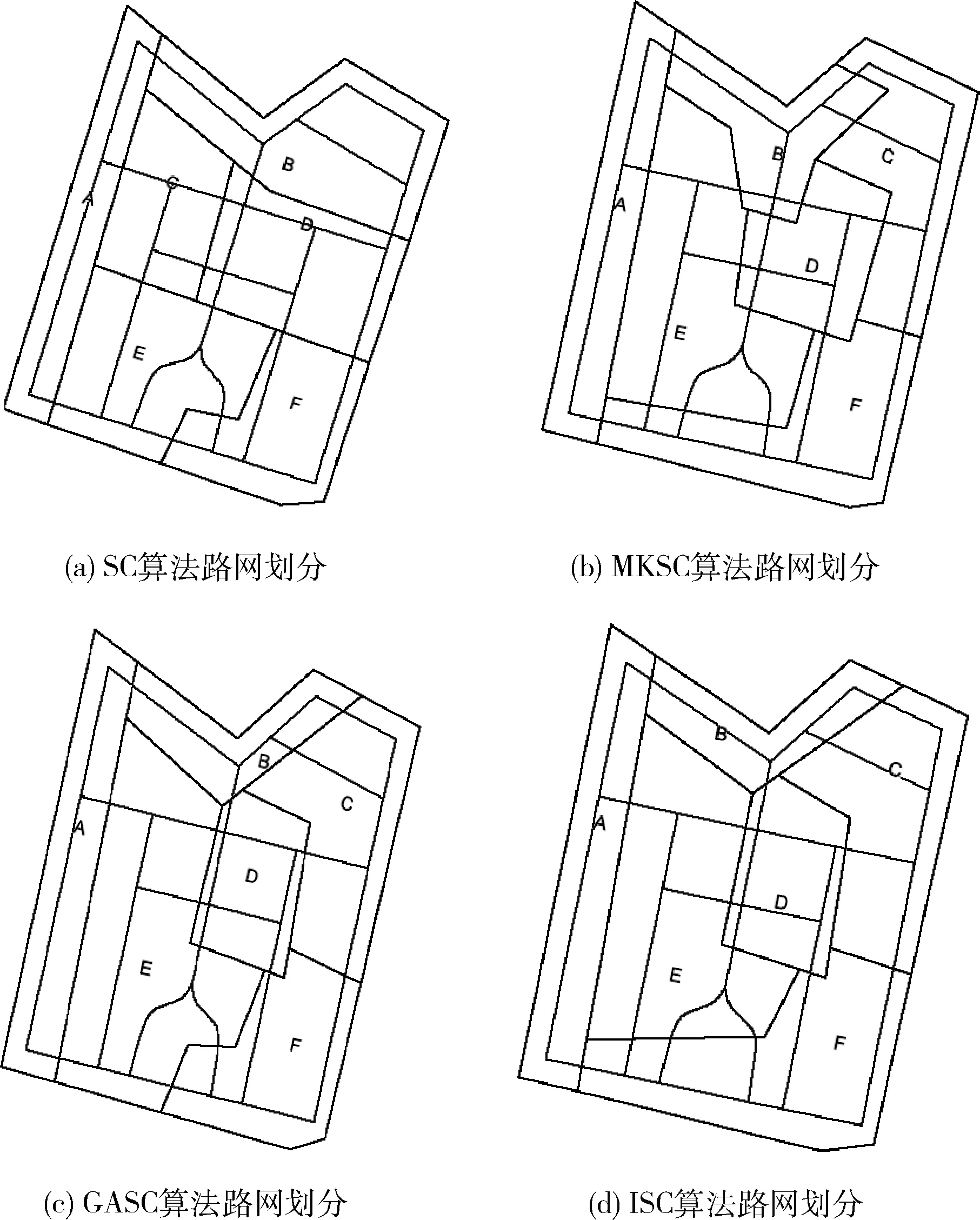
图8 路网划分结果

从路网划分结果可以看出，如图8(a)所示，传统谱聚类算法在路网划分时在空间上虽然各个子区域相连但聚类精度较低，粗略地将路网划分成多个独立子区。如图8(b)所示，MKSC算法考虑了复杂的路网结构特征，在传统的谱聚类路划分方法的基础上利用路网子区之间复杂的关联关系进行路网子区域之间的划分，形成了多个空间分布上更加紧密的路网子区。如图8(c)所示，GASC算法在传统谱聚类算法基础上结合遗传算法，以一个较大概率寻找全局最优解进行路网划分，生成了子区域之间具有较大差异性的路网。如图8(d)所示，本文所提出的算法既考虑了路网复杂的关联特性又兼顾了聚类中心的优化，将路网划分成多个内部紧密而子区间相似性较低的路网子区域，表明本文所提出的算法能够有效地对城市路网进行划分。

4 结束语

本文提出基于改进谱聚类算法的交通区域划分方法，从路网结构信息与聚类中心两个角度对传统谱聚类算法进行改进。通过马尔可夫链对相似图重构，考虑了复杂的路网隐含信息，然后结合遗传算法，提高全局的寻优能力，并用实际交通数据进行聚类分析。实验结果表明，ISC算法考虑了复杂的路网结构信息，既有效保证了路网子区内部的同质性又满足了子区之间的差异性要求，聚类效果好于对比算法。文中在特征研究时只考虑了交通流量特征，未来将进一步增加特征因素，例如城市路网兴趣点、人群流量分布等。