基坑降水引起地基沉降计算方法研究
2021-09-16徐良勇
徐良勇
(上饶市科信水土保持监测有限公司,江西上饶334000)
0 引言
近年来,我国城市经济得到了快速发展,许多城市建成了无数高楼,而建立高层建筑物的基础就是需要开挖深基坑[1]。而那些具有丰富地下水的城市中,常由于地下水的影响使得基坑开挖工程的难度增大。因此,为避免渗透破坏及围护结构的侧压力过大,通常会在基坑开挖时对基坑进行降水处理。
在基坑降水过程中要防止出现地基土流失以及基坑附近处的建筑物地基发生沉降和倾斜等不良情况。一般情况下,地基下部土层的岩性不是单一的,在进行降水处理时需根据不同含水层的岩性特征采取对应的措施,否则基坑会出现泥砂排量过高,破坏地层结构,进一步破坏地基的稳定性。此外,地基土层中孔隙水压力减小使得施加在地基土层的附加应力增加,从而使得土层被压缩,也是导致地基沉降的原因之一[2,3]。因此,在对基坑采取降水措施时,首先要考虑地层含水特性、基坑降水量及其附近有哪些建筑物等因素,然后根据基坑附近处地基的沉降及沉降差来对地基稳定性进行评估,最后根据计算结果来确认该计算方法是否对基坑降水具有可行性。
1 地基沉降计算的理论公式
当井点降水仅出现少量的泥砂排除现象时,并且附近的地基在水位降低深度内,则可用分层总和法对砂土含水层与粘性土弱含水层组成的地层进行沉降量的计算。各土层沉降量叠加即为地基的总沉降量。其中,不同土质土层的计算公式如下:
砂土的沉降量计算公式:

粘性土及粉土沉降量的计算公式:

式中:S∞——最终沉降量,cm;H——土层厚度,cm;△p——作用地基上的附加应力,MPa;E——砂土的弹性模量,MPa;a——粘性土或粉土的压缩系数1/MPa;e0——粘性土或粉土的初始孔隙比。
式(1)中的参数a,e0及E均可由岩土工程勘察报告获取,而参数△p及H由于在不同岩性和计算目的条件下,其取值会有所不同,故需对这2个参数进行探讨。
2 △p不同取值的依据
水位下降作用在地基上的附加应力△p,其值为水位降低的高度△H与水的容重γw的乘积,即:

抽水过程中,基坑降水产生的漏斗状曲面会逐渐趋于稳定,因此,基坑不同部位及其附近地基的水位下降值会有所不同,假设计算点处水位下降值为△H′,即有:

式中:H0——潜水含水层厚度或承压含水层水头,m;Hr——算点水头,m。
2.1 △p在砂土层中的取值
△p按式(4)计算,将式(4)代入式(1),得到不同计算点地基的沉降量,由于不同计算点的沉降量有所差别,因此,有必要进行地基沉降差的计算。
计算点水位下降值取影响带内的平均水位下降值与水的容重进行计算,即:

式中:△Hˉ——计算点水位下降影响带内的平均水位下降值,即基坑水位下降高度△H与影响边界△H=0的平均值,

再将式(7)代入式(1),得到了降水影响带内的平均沉降量,该结果对地基稳定性评估无太大意义,可不作考虑。
2.2 △p在粘性土中的取值
粘性土粒径和孔隙均较小,并且孔隙中的水存在的形式主要以结合水和重力水为主。在无特殊条件影响情况下,粘性土中的孔隙处于半封闭半贯通状态,而处于贯通状态的孔隙可以通过重力水传递静水压力。因此,为准确得到水位下降时施加在土层上的附加应力,需在式(4)中添加孔隙贯通率k进行修正[4],

粘性土中孔隙度n与孔隙中的水、孔隙贯通及孔隙封闭的体积相关,所以有n>k,而k值的计算比较困难,从理论角度上讲,k与粘性土的容水度c、给水度μ及持水度α密切相关。一般情况下,当粘性土土体含水饱和时,其c与n相差不大,即有n=c。
以上参数中,为在重力作用下,土层中所能持有的水量与该土层体积之比,而在重力作用下结合水受到影响极小,由此可知,在重力作用下,土层最大含水量等于最大结合水量。为在重力作用下,土层中能够任意流出的水量与该土层的体积之比,其数值:

综上分析可知,用μ代替k是可行的,因此,式(8)可改写为:

由式(9)可知,μ为c减掉了结合水的体积,但是没有减去封闭孔隙的体积,所以用μ代替k进行附加应力的计算是比较保守的。
采用式(9)进行估算时的条件为缺乏μ实测资料,式(9)中,c可通过岩土工程勘察报告获取,若不能从报告中获取,则可将孔隙比e和c进行换算,即:

一般情况下,土层颗粒越细,其α越高,当颗粒粒径在0.050~0.005mm时,取α=0.102;当颗粒粒径 小于0.005mm时,取α=0.449。为计算方便,当土层为粉土时,可取α=0.10,土层为粘土时,可取α=0.45,土层为粉质粘土或重粉质粘土时,α可取0.10~0.45的中间值,为方便计算,后面土层为粉质粘土或重粉质粘土时,取α=0.10。
将式(10)代入式(2)可得:

式(12)即为计算点的地基沉降量。
3 计算土层厚度H的取值
计算土层厚度H的取值需先对现场的水文地质条件及环境条件进行分析,再根据下列原则考虑:
1)对于降水面以下的土层,几乎不会因为水位变化而发生固结沉降,所以在计算时仅考虑计算点的降水面以上土层的沉降量。
2)当现场地下水位变幅明显时,由于水位常年都在变化,导致该段的土层基本上达到了最大压缩量,所以在计算厚度时通常不考虑该情况。
3)计算地基沉降是为了能够准确评价地基的稳定性,由于地基以上的土层厚度不会对地基稳定性产生不良影响,因此,可忽略建筑物基础以上的土层厚度。
4 △H′的计算方法
4.1 用潜水完整井浸润曲线方程确定△H′
式(4)中Hr可采用潜水完整井浸润曲线(图1)方程进行计算:

图1 潜水基坑完整井剖面图
将式(13)进行移项处理,得到:


式中:Hr——距基坑边距离为r处的水头,m;hw——井点稳定的水头值,m;S——基坑水位下降值,S=H0-hw;r0——基坑仿大井半径;r——以基坑边至计算点的距离;R——基坑降水时的影响半径,m;K——渗透系数。
4.2 用地下水向承压—无压井流动确定△H′
测量基坑大井涌水量时可考虑在“a”区范围内为地下水无压流动,超过该范围即为有压流动。因此,采用分段法将水流看做为以a为半径的虚构大井,其影响半径为R+r0。再在大井内假设还有一个以“r”为半径的基坑大井,影响半径为a,如图2所示。

图2 无压—承压基坑完整大井剖面图
上述中,采用分段法时两者的流量可表示为
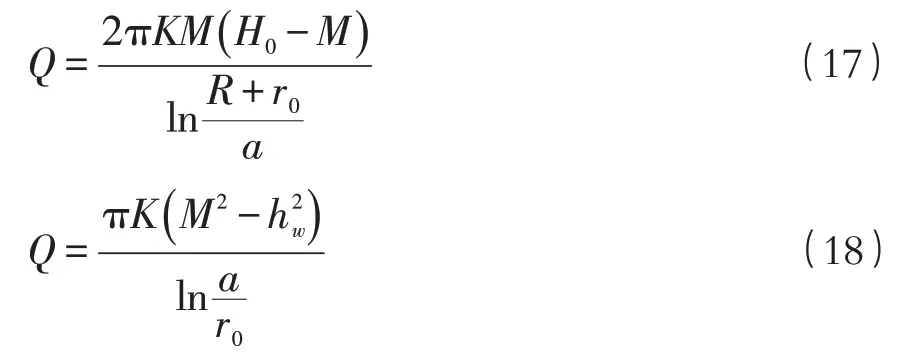
将上式联立消去a,得到基坑仿大井的涌水量计算公式:

无压地段浸润曲线计算式为

承压地段的水头计算式为
式中:M——承压含水层厚度,m;H0——承压含水层的水头,m;r1,r2——无压段和有压段的计算点到基坑井点的距离,m;a——基坑中点到无压运动转有压运动断面的距离。其中,a可由式(18)进行移项处理,得到:
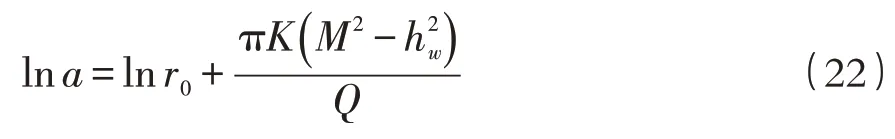
5 工程算例
以江西某小区住宿楼基坑降水时对3单元楼地基沉降评价为算例。以基坑降水设计计算为基础,对基坑降水导致周围建筑物地基沉降进行计算。各参数与地层岩性等见图3,潜水静水位埋深2.00m。

图3 地基沉降计算剖面图
5.1 距基坑r1处的地基沉降量
将图3中已知条件代入式(16)可得Hr10=7.43m,由式(5)可得△H′=H0-Hr10=12.00-7.43=4.57m,即计算段的厚度为4.57m。其中,根据图3可以得到,②号土层(粘质粉土层)厚度H2=1.85m,则处于水位以下②号土层厚度为H2′=1.85-(2-1.4)=1.25m,③号土层(粉砂层)的计算厚度H3′=4.57-1.25=3.32 m,小于③号土层厚度H3=3.44m。a=0.2/MPa,e=0.62,n=0.38,E=85MPa。根据分层总和法计算每层土层的沉降量。
按公式(2)计算②号土层(粘质粉土层)的沉降量,根据式(9)及(10)可以得到μ=0.38-0.1=0.28,△p=0.28×4.57×1×10-2=0.0128MPa。计算得S1=0.197cm。
按公式(1)计算③号土层的沉降量,根据式(4)可以得到△p=4.57×1×10-2=0.0457MPa,计算得到S2=0.178cm。
则距基坑为r1处的地基沉降量为s∞10=s1+s2=0.197+0.178=0.375cm。
5.2 距基坑r2处的地基沉降量
计算方法同r1处的地基沉降量,计算得到Hr55=12.36m>H=12.00m,由此可知,该处已超出基坑降水时的影响半径R=49.10m,未发生水位下降(△H′=0),因次,此时的地基沉降量s∞55=0。
5.3 地基稳定性评估
通过计算可知,3单元楼距基坑最近的点r1及最远点r2的沉降差为0.375cm,r1和r2之间的距离为45.00m,倾斜率为8.3×10-5。根据规范[5]可知,其差异沉降导致建筑物倾斜在允许范围内,即采用管井围降方法时不会破坏地基的稳定性。同时,施工结果表明,在经过3个月的连续抽降,3单元楼地基未发现任何不良情况。
6 结论
1)地基土层中的孔隙水压力随着基坑水位下降而下降,相反,地基土上的附加应力随着基坑水位的降低而增加,这是导致地基发生沉降的主要因素。
2)在不同土质的地层中,静水压力的传递方式有所差异。粘性土中的孔隙需贯通土层,在孔隙中传递静水压力。因此,在计算粘性土的附加应力时,需结合孔隙贯通率加以修正。通过计算可知,孔隙贯通率与粘性土层的给水度相差不大,且后者更容易获得,所以在缺乏孔隙贯通率时,采用给水度对粘性土附加应力进行修正具有实际意义。
3)对基坑周围建筑物地基稳定性进行评估是计算地基沉降量的主要目的,基坑不同部位及其附近处的地基水位下降值不同,根据本文采用的计算公式,对不同水文地质条件,可根据降水方案选取相应的公式,从而得到降水影响带内不同计算点水位下降值,最后根据计算结果对基坑附近地基的稳定性进行评估。
