青海高原牦牛体重分布Johnson正态化转换体系研究及应用
2021-09-15孙静韩学平
孙静,韩学平
(1.青海省海晏县畜牧兽医站,海晏 812200;2.青海省畜牧总站,西宁 810001)
生物统计学中,试验数据的处理和统计分析基本都是基于试验结果符合正态分布的假设[1]。但并非所有试验结果都能通过正态性检验。任何试验结果都会因为测定方法的局限或人为因素导致误差,科学的剔除异常数值是提高试验结果准确性的必要步骤。异常数据的剔除方法分为经验判断法和统计识别法。经验判断法就是根据试验者长期的工作经验对异常数据进行剔除的方法;统计识别法是给定一个置信概率,并确定一个置信限,凡超过此限的误差,就认为它不属于随机误差范围,将其视为异常值剔除。当物理识别不易判断时,一般采用统计识别法。常用的统计识别法有拉依达准则法(3δ)、肖维勒准则法(Chauvenet)、狄克逊准则法(Dixon)、罗马诺夫斯基(t检验)准则法、格拉布斯准则法(Grubbs)等。为了将这些不符合正态分布的试验结果转换为正态分布,常用的方法有取倒数、开平方、取对数等。但在实际处理中经常遇到转化效率低的问题。为此,本文采用Johnson 正态转化体系进行转换,获得了良好效果。
1 材料与方法
1.1 时间与地点
2014年10月至次年2月分别在青海省玉树州曲麻莱县、海南州同德县和黄南州泽库县进行现场测定,共测定约2岁青海高原公牦牛540头,其中曲麻莱县190头,同德县146头,泽库县204头。
1.2 测定项目与方法
牦牛测定项目包括体重(kg)、体高(cm)、体斜长(cm)、胸围(cm)和管围(cm),测定方法根据陈伟生(2005)[2]方法开展。
1.3 数据异常值的剔除与Johnson正态转化体系
1.3.1数据异常值的剔除
本文以青海高原牦牛体重数据为研究对象,借助Minitab 17 采用格拉布斯准则法(Grubbs)对异常数据进行识别和剔除,显著水平为5%,备择假设最小或最小数据为异常值。
1.3.2Johnson 正态转化体系
以随机变量X为代表任意连续性状的测定结果,则Johnson转化体系的三族公式及参数范围见表1。
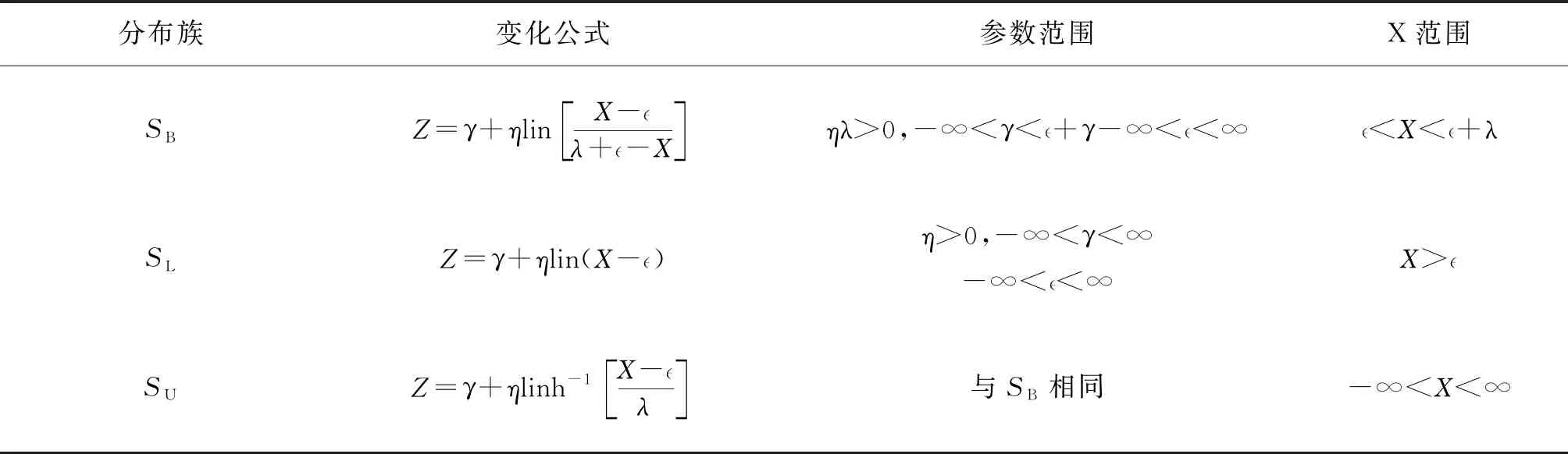
表1 Johnson 分布的种类与转化体系
其中:SB、SL和SU分别表示X是有界的、对数正态的和无界的。η,λ>0是尺度参数,γ,ε为形状参数[4]。利用这三族函数可以将非正态分布的数据X转化成标准正态分布的数据Z。但具体使用时,必须要从三族函数中选择一个进行转换。具体的函数选择方法和参数确定方法根据卓德保等[5](1999)方法进行。
1.4 Johnson 正态转化与正态性检验
本文以青海高原牦牛2岁公牛体重分布为研究对象,借助Minitab 17 进行Johnson正态转化,选择P>0.1为最优转化。数据的正态性检验借助SPSS 22进行。正态函数的计算调用Microsoft Excel 2016中相关函数。
2 结果与分析
2.1 异常数据剔除结果
青海高原牦牛体尺和体重指标异常数据剔除前和剔除后的数据统计结果见表2。
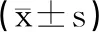
表2 青海高原牦牛异常数据剔除结果
从表2、表3可以看出,采用格拉布斯准则法(Grubbs)剔除了8组异常数据,从而使数据的变异性有所降低,体斜长的变异系数从4.43%降到4.08%,胸围变异系数从4.81%降到4.38%,体重变异系数从13.15%降到11.00%。

表3 青海高原牦牛异常数据剔除前后变异系数
2.2 Johnson 正态转化结果
经Minitab 17 Johnson正态转化,输出结果为最优标准正态分布百分位点 z=0.71,选择三族函数中的SU,具体转化公式如下:
经转换后,X~N(0,1)的标准正态分布。转化前后的数据分布图分别见图1 和图2。
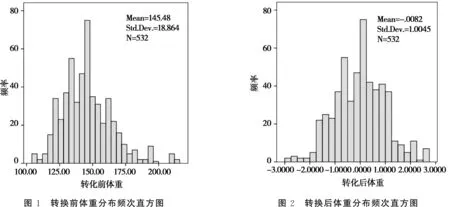
转换前后的概率分布图分别见图 3 和图 4。转化前后的数据利用Shapiro-Wilk方法进行正态性检验,转换前得到的W统计量为0.964,显著性检验概率P=0.000,证明原数据不符合正态分布;转换后得到的W统计量为0.996,显著性检验概率P=0.157,证明转换后的数据符合正态分布。
2.3 转化后正态分布在选种中的利用
经Johnson转化后,牦牛体重呈平均数为0,标准差为1的标准正态分布,既X~N(0,1)。该转换后的分布可以用于牦牛育种工作,制定相应的选种标准,预测育种进展,制定育种计划。假设青海高原牦牛2岁留种率为17%,本文仅以体重为选种指标,则可以通过调用Excel 2016中正态分布计算函数NORMSINV(17%),计算出对应的转换后体重为0.9961,再从原始体重与转换后体重对照表中找出最接近的原始体重,即164kg,说明选种时只要选择体重在164kg以上的种牛留种,就可满足留种的需要,同时可以用上述方法估计留种群的平均体重为171kg,这样选种的选择差为25.5kg(选择差是留种的个体体重均值与畜群体重平均数之差,体重均值见表2),如图5所示。
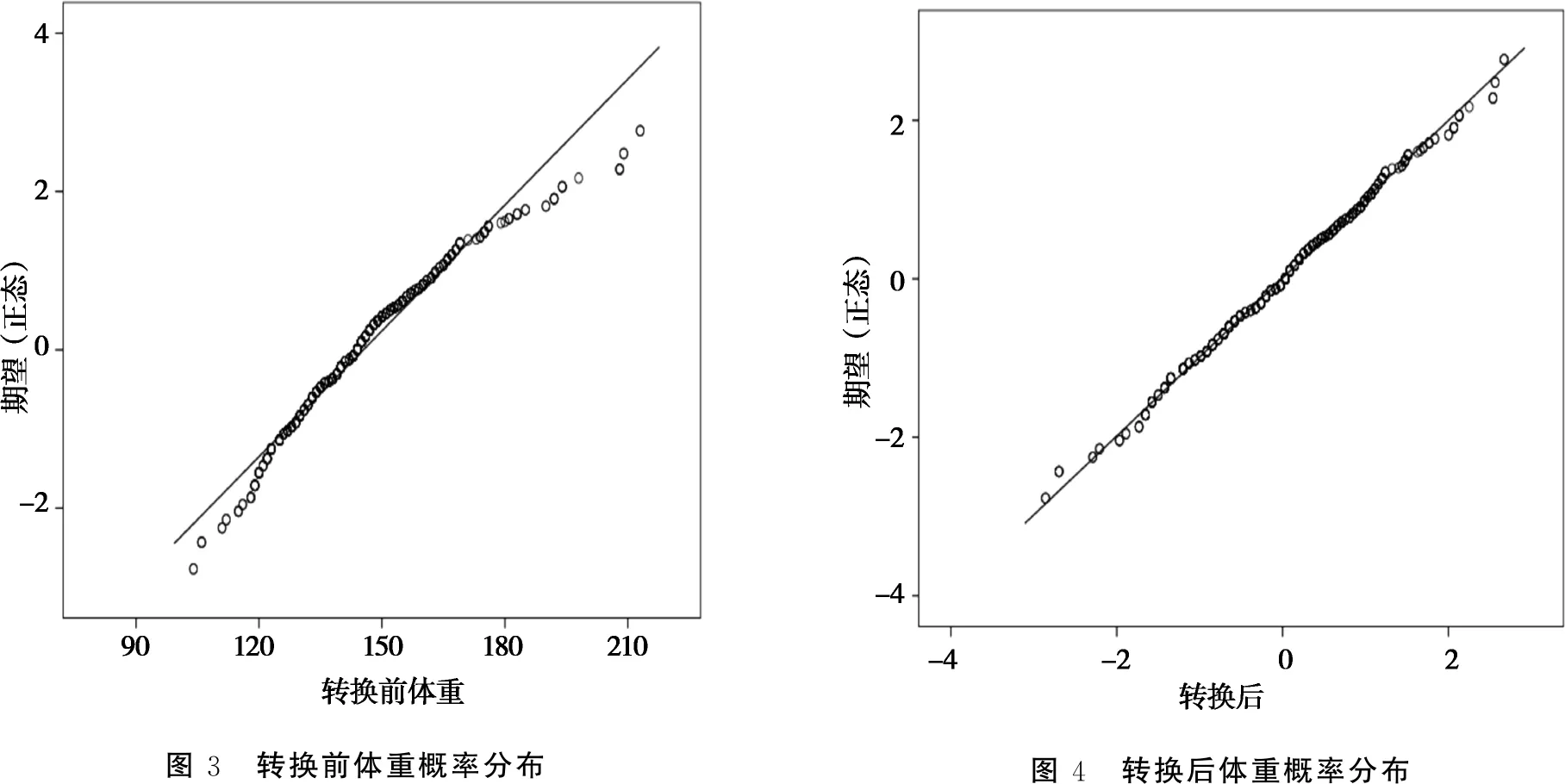
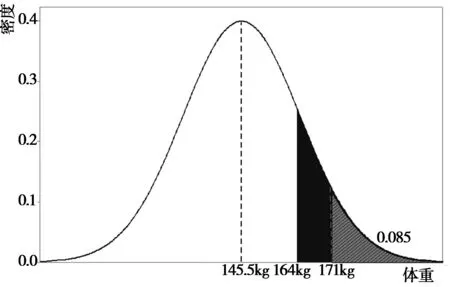
图 5 体重分布密度及选择效应
3 结论与讨论
Johnson转化体系的实用过程就是在原始分布的基础上从Johnson分布的三组函数中选出最接近正态分布的转化形式,并确定其相应的参数,然后利用确定的转化函数进行转化。本文数据在常用的取倒数、开平方、指数函数等转化方法不能有效转化的前提下采用了Johnson转换体系,取得较好效果。
Johnson转换体系的使用和最优转化形式的确定是一个复杂的计算过程,尤其是最佳z的确定更是要重复计算101次,这使得计算量更加巨大[6,7]。而本文采用Minitab 17的Johnson转化功能,快速实现了试验数据的正态化转化,为数据的分析和研究利用提供了快捷的工具。
在数据正态化处理的基础上,根据生产需要以及社会、科技、经济条件确定选种率,从而制定相应的选择标准。当然品种标准的制定除了考虑品种的外貌特征要求外,还要综合考虑体尺和体重指标。
