“三软”煤层巷道底板破坏深度计算与底鼓控制

刘玉卫,商铁林,张 沛,张亚峰,龚 剑,刘应然

(1.郑州工程技术学院, 河南 郑州 450044；2.郑煤集团工程技术研究院, 河南 郑州 450042；3.榆林学院, 陕西 榆林 719000；4.西安科技大学, 陕西 西安 710054)

“三软”煤层巷道的支护问题一直是困扰煤矿安全生产一大技术难题，由于其围岩条件差，支护不当，易造成巷道失稳破坏。过去对软岩巷道顶板围岩的研究较多，如最初的普氏压力拱假说(1907)和太基公式(1942)、卡斯特纳公式(1948)[1]，后来考虑支护体与围岩作用关系的锚杆支护方式——“组合梁、加固拱”等理论[2]，以及近年来的围岩松动圈理论[3-4]、关键圈理论[5]等，这些理论主要从顶板的破坏为出发点加以研究，而从底板研究”三软”煤层巷道的理论相对较少。最早研究巷道底鼓的是前苏联的秦巴列维奇N·M[5]，认为巷道底鼓可看作是两个压模传递给松散体的底板上的荷载作用下压出的现象；德国的奥顿哥特M[6]则认为，巷道两帮岩体在垂直应力的作用下被压裂，巷道顶底板在水平应力的作用下向巷道内鼓出；曲永新[7]等人认为巷道底鼓的本质是底板泥岩的遇水膨胀；康红普[8]认为巷道底鼓的原因在于失稳的底板岩层向巷道内的压曲，偏应力作用下的扩容以及岩石遇水膨胀；贺永年、何亚男[9]认为底鼓是由于巷道两帮岩柱传递顶板压力，两帮围岩在挤压底板的同时一起下沉，底板在严重挤压变形的情况下发生断裂,然后底板隆起。本文综合国内外以往对底鼓机理的研究成果，在不考虑遇水膨胀的情况下，且将”三软”煤层巷道围岩看作抗拉、抗弯、抗剪能力都极其微弱的理想松散体加以研究。

1 底板破坏深度计算

不考虑遇水膨胀情况下，巷道在开挖后底板岩层局部应力得到卸载，其它应力则主要通过巷道两侧帮岩体向下进行传递，假设巷道底板两侧帮内受重力均布荷载q=γH的作用(理想状态下左右均布对称)，按照朗肯土压力理论，底板岩体在均布荷载q的作用下，MFD区岩体会处于主动塑性应力状态，而MOD区岩体则处于被动塑性应力状态，这样会产生向上的底板围岩挤压应力T，当挤压应力超过底板岩体的屈服强度时，导致OD面破坏，底板就会产生向巷道内的塑性变形，向上隆起或者挤压流入到巷道内造成底鼓，受力模型[10-12]如图1所示。

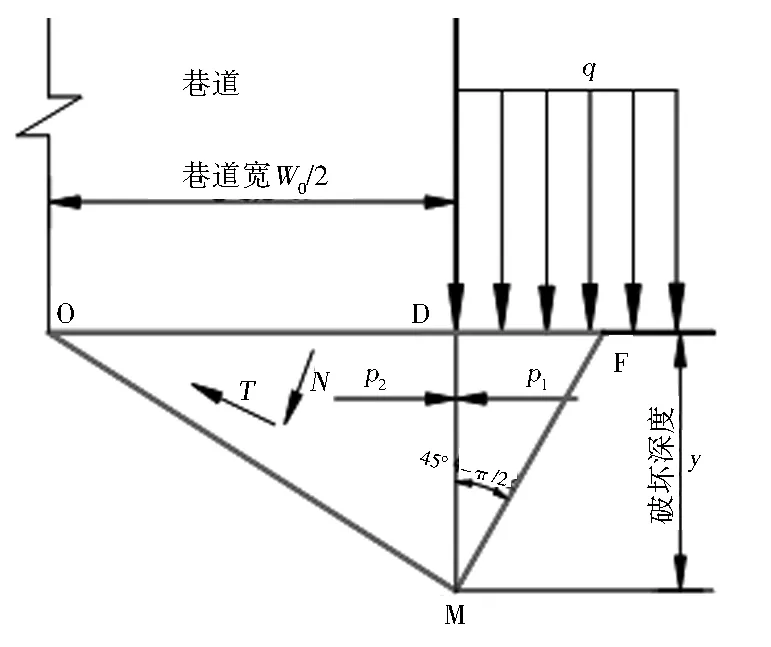
图1 巷道右侧底板受力分析

当巷道岩体处于极限平衡状态时，主动塑性应力区MDF的滑动面MF与水平线的夹角为45°+φ/2，被动塑性应力区域MDO的滑动面MO与水平线的夹为45°-φ/2。假定MD为理想中的分界面，根据朗肯土压力理论[12]，则MD分界面上各点上所受的主动应力和被动应力分别为：

在M点以上的MD范围内，因为σa>σp，底板岩体处于塑性应力状态；在M点以下，σa<σp，底板岩体处于弹性应力状态；在M点处，σa=σp，底板岩体处于极限平衡状态。在M点极限平衡状态时，可求得巷道底板极限破坏深度y，即，当σa=σp时，有γ·yKp=(q+γ·y)Ka，整理得：

2 巷道底板底鼓量公式推导

由上式可知[10-12]，在底板下部y以上的岩体将有可能发生向上鼓起，而y以下的岩体将不会出现移动。当极限平衡状态被打破以后，MDF区域的岩体处于主动滑移压力状态，而MOD区域的岩体处于被动受压应力状态，MD上所受的主动压力P1和被动压力P2的差值，就是推动MOD区域岩体向左滑动的实际推力Δp，则有：

Δp=p1-p2

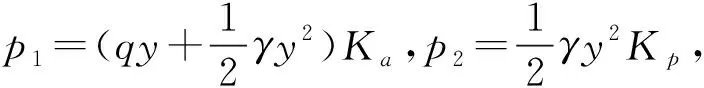
则沿滑动面MO的有效滑移力T1为：

T1=T-Ntanφ

当T1>[T]时，其中[T]为岩体的最大抗剪强度，底板岩体发生底鼓破坏。

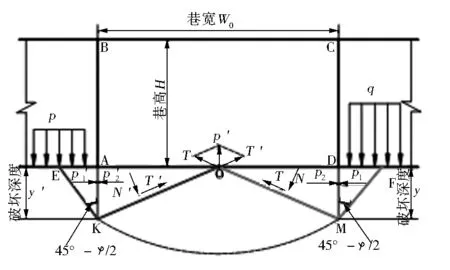
图2 巷道底板综合受力分析

巷道底板两侧滑动面以上的有效滑动力分别为T、T＇，它们的合力为巷道的底压力P＇，T、T＇在x和y轴上的分力分别是px和py；

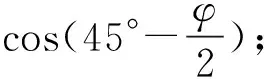
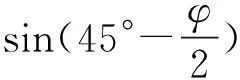
则底压力p＇为：

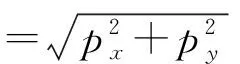
3 实例及应用

以郑煤集团公司告成煤矿21051工作面回采巷道为例，求巷道底板破坏范围及底鼓量，21051工作面下副巷平均埋深约460 m。主采二1煤层，厚度4.2 m，倾角约10°，结构简单。煤层直接顶中下部为细粒砂岩，老顶为中细粒长石、石英砂岩，厚7 m左右；底板为砂质泥岩，厚5.1 m。21051工作面下副巷断面为直墙半圆拱型，断面宽5 000 mm，高4 300 mm，净断面约13.0 m2。

3.1 锚网支护基本参数

原岩应力：q=γh=0.023×460=10.6 MPa。

煤层：抗压强度σc=2.6 MPa，抗拉强度σt= 0.31 MPa。

综合顶底板性质：抗压强度σc=105 MPa，抗拉强度σt=6.8 MPa。

巷道：巷帮高度hw=1.8 m，宽度W0=5.0 m。

3.2 巷道顶板破坏高度确定

借助西安科技大学黄庆享教授的极限平衡拱公式[13-14]，求巷道顶板的破坏深度。

平衡拱：

极限平衡拱：

3.3 巷道底板破坏深度计算

γ取2 600 kg/m3；均布荷载q取q=10.6 MPa；岩体的单轴抗压强度σc为105 MPa；φ经计算取为84.6°；主动土压力系数Ka经过计算为0.2；被动土压力系数Kp经过计算为0.67。

则巷道底板计算的最大破坏深度为：

计算巷道的底鼓μ的公式为：

由于p＇是T和T＇的合力，求解p＇得：

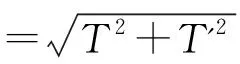
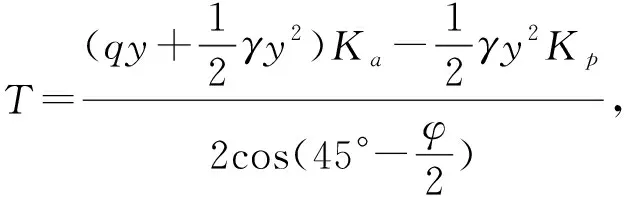
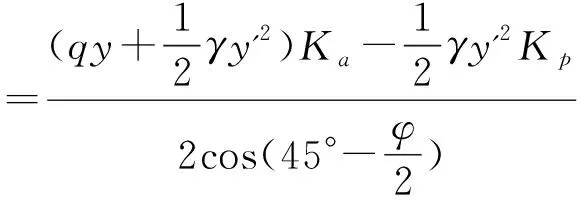
在y=y＇时，求得

=2×107kN；

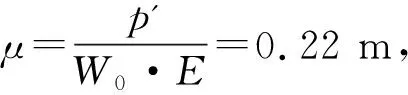
3.4 确定锚杆长度和间排距

根据自稳平衡拱高度为2.5 m，极限状态平衡拱为3.0 m，因此可设计锚杆长度为2.8 m。按照锚杆支护的组合拱理论，在软岩条件下设计形成组合拱厚度为2.0 m。

则锚杆间排距a取值为：a=l-b-c=2.8-2.0-0.1=0.7 m。

式中：l为锚杆长度；b为组合拱厚度；c为锚尾外露长度。

因此，确定锚杆长度为2 800 mm，锚杆间距和排距均为700 mm。

根据底板破坏公式的计算，确定底板加强锚杆的长度为2 000 mm。

3.5 锚网支护布置方案

巷道断面支护方案见图3。

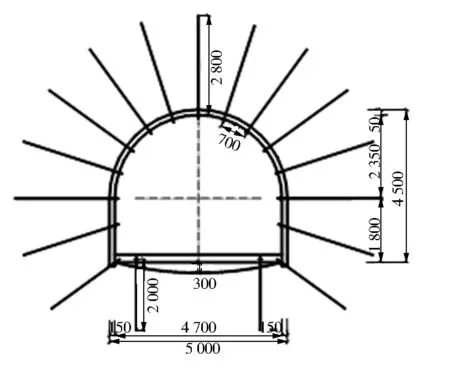
图3 巷道断面支护方案

3.6 围岩松动圈测试

采用YTJ20型岩层探测记录仪，对告成煤矿21051工作面回采巷道围岩进行松动圈测试。在21051工作面回采共布置两个测点，见图4。

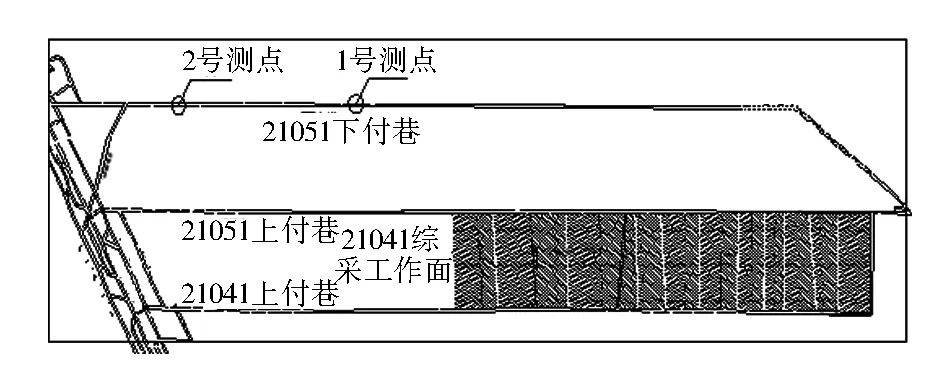
图4 松动圈测点布置位置

从测点1(见图5)测试结果可以看出，煤体的最高声速为2 139 m/s，而最低声速为947 m/s波速随孔深均有逐渐增大的趋势，在距孔口1.6 m左右范围内波速较小，距孔口距离大于1.6 m的区域波速较大，并且波速基本相对恒定在1 720 m/s左右。分析得出，距离孔口大于1.6 m的区域煤体较完整，没有受到扰动，而小于1.6 m的区域裂隙较发育，所以由图5初步确定煤帮的松动范围为1.6 m左右。

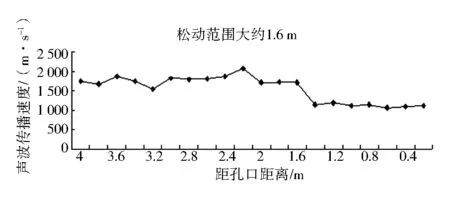
图5 测点1声波传播速度趋势

从测点2(见图6)测试结果可以看出，煤体的最高声速为1 984 m/s，而最低声速为956 m/s波速随孔深均有逐渐增大的趋势，在距孔口1.4 m左右范围内波速较小，距孔口距离大于1.4 m的区域波速较大，并且波速基本相对恒定在1 350 m/s左右。分析得出，距离孔口大于1.4 m的区域煤体较完整，没有受到扰动，而小于1.4 m的区域裂隙较发育，所以由图6可以初步确定煤帮的松动范围为1.4 m左右。素描图见图7。

图6 测点2声波传播速度趋势

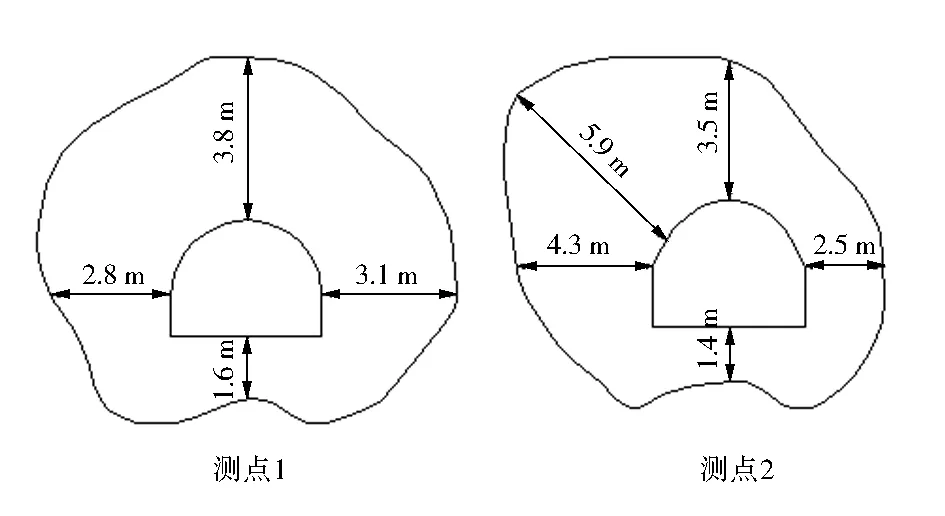
图7 松动圈测试素描

由松动圈测试得到底板的破坏在1.6 m左右，结合理论分析计算可知，底板破坏深度基本一致。

3.7 支护效果检验

按照3.5节是锚网布置方案，进行现场围岩监测。在相邻的21051上副巷设置3个测点，监测结果如下。

通过巷道底板治理前后监测曲线表明(图8)，采用设计优化方案后，巷道底鼓量明显降低，底板稳定得到了较好的控制。

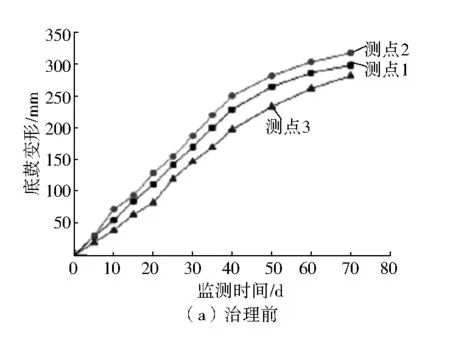
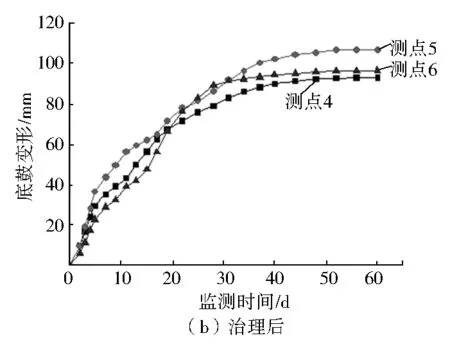
图8 底鼓变形量曲线

4 结 语

1) 对巷道底板破坏力学模型分析得到，底板的破坏深度随有效滑移力的增大而增大，当破坏深度达到一定值后会引起帮的失稳。

2) 当挤压应力超过底板岩体的屈服强度时，导致巷道底板破坏，底板就会产生向巷道内变形，向上隆起或者挤压流入到巷道内造成底鼓。

3) 通过松动圈测试及实际监测数据与理论计算作对比可知，实际底板破坏深度在1.6 m左右，发生的底鼓量在250 mm左右，这与理论计算值较为接近。

4) 基于理论计算的新方案设计能够有效的控制巷道底板的变形破坏，有利于控制巷道围岩稳定，为“三软”煤层巷道支护提供了新方案。