光伏阵列风荷载干扰效应风洞试验研究

马文勇，马成成，王彩玉，韩晓乐，高 飞

1.石家庄铁道大学 土木工程学院，石家庄 050043

2.河北省风工程和风能利用工程技术创新中心，石家庄 050043

3.河北鲲能电力工程咨询有限公司，石家庄 053700

0 引 言

光伏板采用的轻质板和支架结构形式，导致其容易受到风荷载的影响发生破坏。目前我国光伏板风荷载取值的主要依据是《光伏支架结构设计规程》（NB/T 10115—2018）[1]，其给出了倾角在55°以内的光伏板的风荷载取值，但对光伏阵列风荷载取值的规定比较简单，难以满足实际应用的需求。

对于单个光伏板的体型系数取值目前已经有比较充分的研究[2-6]。研究人员还考虑了阻塞率[7]、端部开口[8]对光伏板风荷载取值的影响，并且采用数值模拟手段获得了光伏板周围的流场特性[9]。总的来说，对于不同倾角、不同风向角下单个光伏板的体型系数取值目前已经比较明确。

与单个光伏板不同，由于干扰效应，光伏阵列中不同位置光伏板的风荷载取值有明显的差异。高亮等[10]以风洞试验为主，并结合数值模拟方法，研究了光伏板倾角、高度、间距、方阵中的位置等对其风荷载体型系数的影响规律，提出了考虑各种影响因素的风荷载计算公式。江继波等[11]利用数值模拟方法，分析了风向角、光伏板安装倾角和光伏板纵向间距对光伏阵列风荷载及其所受弯矩的影响。Jubayer等[12]通过数值模拟研究了不同风向角对地面光伏阵列风荷载的影响，发现在所有风向角下第1排光伏板承受风荷载最大。Warsido等[13]通过风洞试验研究了不同间距参数对地面光伏阵列风荷载的影响，发现光伏板上的风荷载随其纵向间距的增大而增大。虽然目前已经有了部分光伏阵列风荷载的研究，但由于光伏阵列影响参数比较多，风荷载干扰效应比较复杂，关于光伏阵列风荷载的取值规律仍然不清楚，需要进一步的研究。

为明确光伏阵列中风荷载的折减效应，本文通过刚性模型测压试验，分析上游光伏板对下游光伏板的风荷载干扰效应，对比不同位置光伏板的体型系数及风荷载分布规律，并给出遮挡状态下光伏板体型系数取值建议，为设计人员提供参考。

1 风洞试验介绍

试验在石家庄铁道大学风洞实验室低速试验段进行。低速试验段长为24 m，宽为4.4 m，高为3 m，风速范围为1～30 m/s，背景湍流度小于1%。

1.1 试验模型

如图1（a）所示，单块光伏板模型长L= 205 mm，宽B= 124 mm，厚T= 7.5 mm，缩尺比为1∶8。单组光伏板由20个单块光伏板组成。模型采用ABS板制成，光伏板上下表面对称布置测压点。单块光伏板有12个测压位置，共24个测压点；单组光伏板有240个测压位置，共480个测压点。图1（b）为光伏板立面图，其中：α为风向角，取值范围为0°～180°，以15°为间隔；β为光伏板倾角，取10°和30°；H为光伏板离地高度，取62.5 mm。

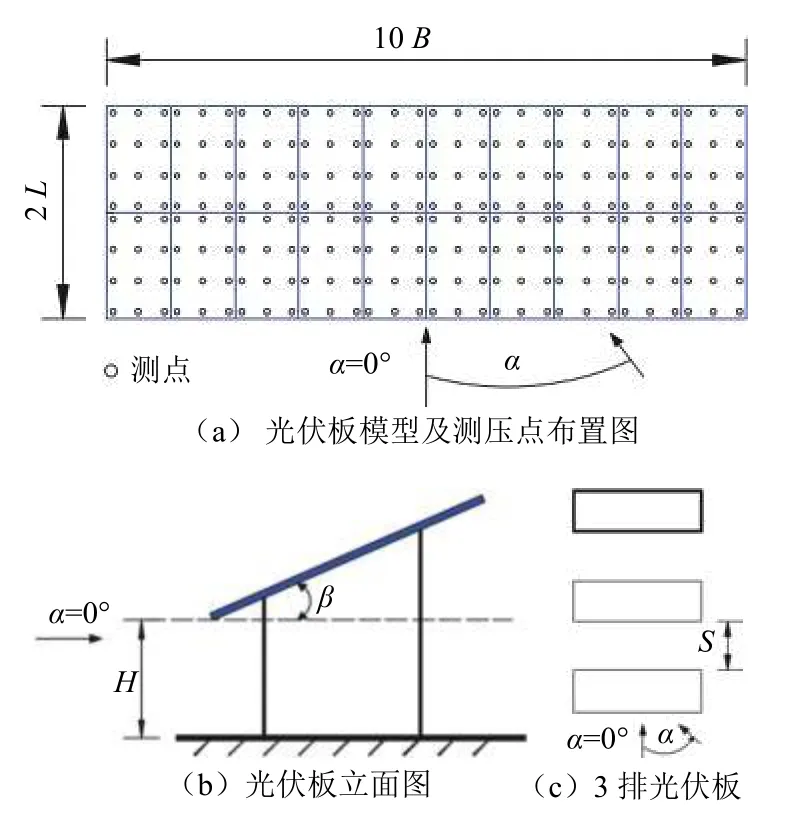
图1 试验模型及参数定义Fig.1 Test model and parameter definition

风洞试验以单组光伏板为基本单元，考虑分别有1、2、3、4、5和6组光伏板等6种串列情况下光伏板风荷载的变化规律。图1（c）给出了3排光伏板时光伏阵列的布置图，光伏板纵向间距S= 730 mm。

1.2 试验工况

光伏阵列常建造在空旷平坦的地区，地面粗糙度处于《建筑结构荷载规范》[14]中的A类地貌和B类地貌之间。本研究偏于保守，选用A类风场。自由来流风速为12 m/s，采样频率为330 Hz，采样时间为30 s，来流风场参数与文献[15]相同。单组光伏板风洞试验，倾角β为10°和30°，风向角α范围为0°～180°，以15°为间隔。单列光伏板风洞试验，倾角β为10°和30°，风向角α范围为0°～30°和150°～180°，以15°为间隔，光伏板组数分别为2、3、4、5和6。试验模型照片见图2，A类风场平均风速剖面和湍流度剖面见图3。由图3可以看出，地面粗糙度指数γ= 0.12，试验模拟得到的风速剖面与我国《建筑结构荷载规范》规定的理论风速剖面吻合较好。

图2 风洞试验照片Fig.2 Photos in wind tunnel test

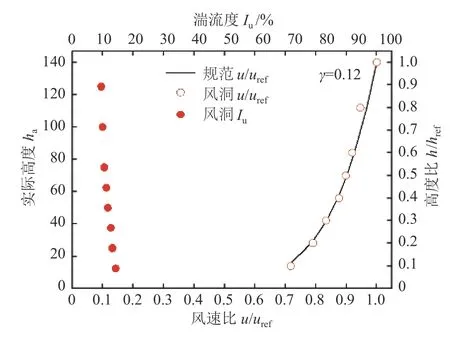
图3 平均风速剖面和湍流度剖面Fig.3 Mean wind speed profile and turbulence intensity profile

1.3 参数定义

风压系数定义：

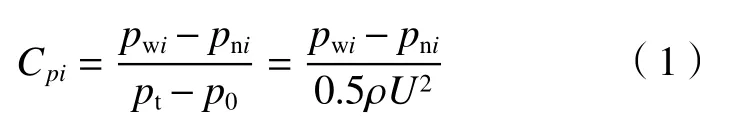
式中，Cpi为测点i处的风压系数，pwi和pni分别为测点i处上表面和下表面的风压，pt为参考点处总压，p0为参考点处静压，ρ为空气密度，U为参考点处风速，参考点高度Z= 10 m。

体型系数定义：

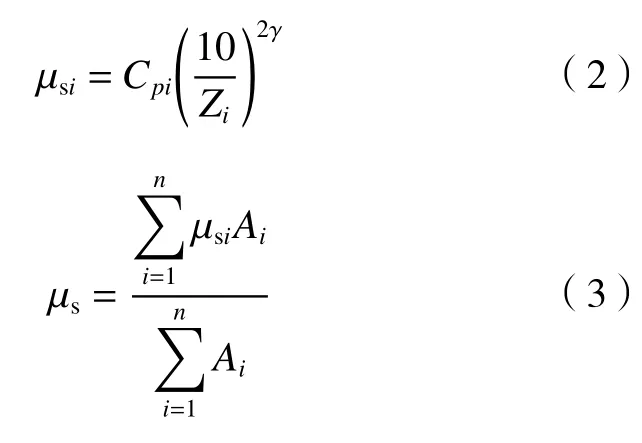
式中，μsi和Zi分别为测点i处的体型系数和高度；μs为光伏板整体体型系数；Ai为测点i的所属面积。

整体体型系数μs（简称体型系数）的正负值规定如下：正值表示风压沿光伏板上表面法线方向向里，此时光伏板承受风压力；负值表示风压沿光伏板上表面法线方向向外，此时光伏板承受风吸力。

2 试验结果

2.1 单组光伏板风荷载分布

图4给出了当倾角β= 10°和30°时，单组光伏板体型系数随风向角α的变化情况。由图4可知，当β= 10°时，光伏板的体型系数随着风向角的增大不断减小，其取值范围为–0.85～0.31。当α= 0°时，体型系数取得最大正值0.31；当α= 180°时，体型系数取得最大负值–0.85。当β= 30°时，光伏板体型系数的变化规律与β= 10°类似，但与β= 10°时相比，光伏板的体型系数显著增大，其取值范围为–1.33～1.07。当α= 15°时，体型系数取得最大正值1.07；当α=150°时，体型系数取得最大负值–1.33。虽然不同倾角下光伏板体型系数最大值和最小值对应的风向角不同，但是其取值与0°和180°风向角下的取值接近，因此α= 0°和180°可近似作为其风荷载取值的最不利工况。

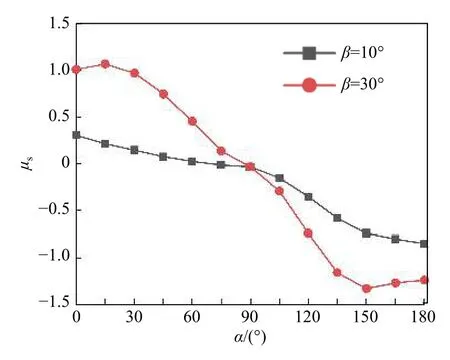
图4 体型系数随风向角变化情况Fig.4 Variation of pressure coefficient to wind angle

图5给出了倾角β= 10°、30°和风向角α= 0°、180°时的光伏板风压分布情况。由图5可以看出，当β= 10°、α= 0°时，光伏板体型系数上半部分最小为0.2，中部为0.4，下部最大为0.8。当β= 10°、α=180°时，光伏板体型系数上部为–2.0，中部为–1.0，下部为0，上部与下部的差距较大。此时，由于存在强烈的气流分离作用，板上部两端体型系数的梯度变化幅度明显，体型系数等值线分布密集。当β= 30°、α= 0°时，光伏板体型系数从上到下呈现明显的梯度变化，体型系数分布均匀，从上部的0.2渐变到下部的2.0。当β= 30°、α= 180°时，光伏板体型系数上半部分最大为–1.6，中部为–1.4，下部最小为–0.6，光伏板两侧的体型系数绝对值小于中间区域。当α=0°时，光伏板下部体型系数绝对值大于上部体型系数；当α= 180°时，光伏板上部体型系数绝对值大于下部体型系数。由此可知，光伏板近风端承受的风荷载大于远风端。

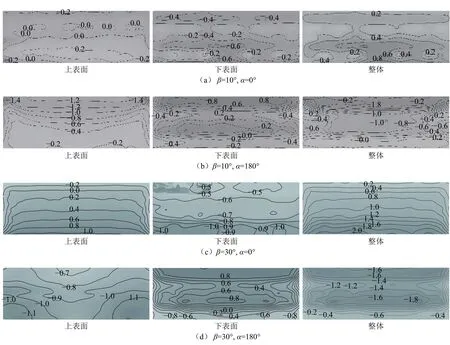
图5 光伏板体型系数分布Fig.5 Distribution of solar panels pressure coefficient

通过对比不同倾角下光伏板体型系数的变化情况发现：最不利风向角出现在α= 0°和180°附近；光伏板近风端承受的风荷载大于远风端；倾角越大，体型系数也越大。

根据试验结果，单组光伏板体型系数为：当倾角β= 10°时，正压取值为0.35，负压取值为–0.90；当倾角β= 30°时，正压取值为1.10，负压取值为–1.35。与《光伏支架结构设计规程》相比，倾角β= 10°时，正压取值远小于规范的0.80，其余情况与规范差距较小。

2.2 光伏阵列风荷载分布

为了研究光伏阵列的干扰效应，以最不利风向角α= 0°和180°为例，图6给出了在不同倾角和风向角下不同位置光伏板的体型系数的变化情况。横坐标代表光伏板所在的排数。

由图6可以看出，不同工况下不同位置光伏板体型系数的变化趋势类似，第1排光伏板的体型系数绝对值最大，其后各排光伏板的体型系数绝对值均有不同程度的减小。以β= 30°、α= 0°为例：第1排光伏板体型系数最大，值为1.01；第2排光伏板体型系数最小，值为0.26；第3排到第6排光伏板的体型系数在0.36左右波动，几乎没有差异。

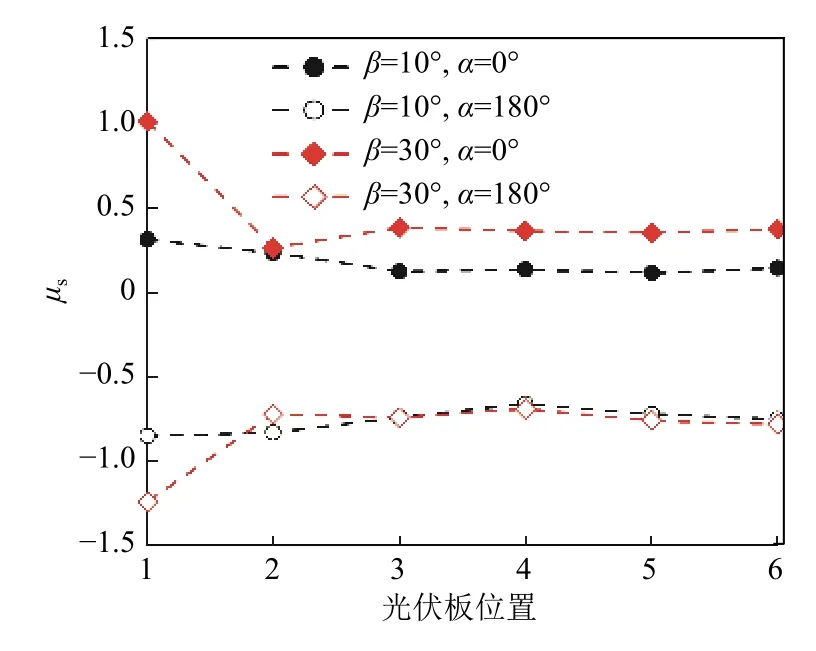
图6 不同位置光伏板的体型系数Fig.6 Pressure coefficients of solar panels at different positions

为更好地表达不同位置光伏板受干扰的程度，以第1排光伏板为参考，引入折减系数Iμ：

式中：μ1为第1排光伏板的体型系数；μi为第i排光伏板的体型系数，i= 1～6。

由折减系数定义可知，折减系数越小干扰效应越强。图7给出了倾角β= 10°和30°时折减系数的变化情况。由图7可知，各工况下折减系数变化趋势大致相同，但在数值上差距较大，且在不同光伏板位置取得极值。当β= 10°、α= 180°时，第4排光伏板折减系数最小，为0.78；当β= 30°、α= 0°时，第2排光伏板折减系数最小，为0.26。由图7还可以看出，随着上游光伏板数量的增加，折减系数逐渐减小，第3～6排折减系数的变化幅度较小，由折减系数的定义可知，第3～6排光伏板的体型系数大致相当。综上所述，可以说明当上游光伏板数量增加时，下游光伏板的体型系数不再随之而发生明显的变化，即上游光伏板对下游光伏板的干扰趋于稳定。

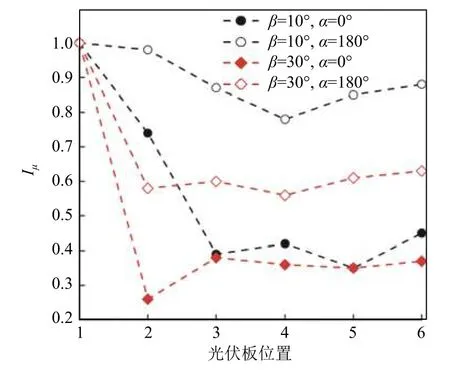
图7 折减系数随着光伏板位置的变化Fig.7 The reduction coefficient changes with the position of the solar panels

通过对比发现，在不同倾角和风向角下，上游光伏板对下游光伏板的干扰程度差异明显。当光伏板倾角β= 30°时，光伏阵列干扰效应明显大于β= 10°的情况，这是因为大倾角光伏板对流场的影响程度更大，使得上游光伏板对下游光伏板的干扰效应更加显著；当风向角α= 0°时，上游光伏板对下游光伏板的干扰效应明显大于α= 180°时的情况。

图8给出了干扰程度最大工况下（β= 30°、α=0°）不同位置光伏板的风压分布情况。其中，第5和6排光伏板风压分布与第4排类似，限于篇幅未给出。

由图8可知，第2排光伏板上部、中部和下部中间区域体型系数均为0.2，下部两端体型系数为1.4；与第1排光伏板相比，其体型系数明显减小，且分布形式发生了显著变化，不再符合梯度分布，而是在下部两端出现了强正压区。这是由于上游光伏板的干扰，使得下游光伏板下部两端气流分离现象远大于其他区域，体型系数等值线分布密集。第3排光伏板上部和中部的体型系数呈现梯度变化，由0.2渐变到0.6，在下部两端出现强负压区，体型系数为1.6。第4排光伏板体型系数的大小和分布形式与第3排相似。通过对比不同位置光伏板的风压分布情况，发现光伏板上部（远风端）的体型系数变化较小，上游光伏板对下游光伏板的干扰效应主要作用在下部（近风端）。

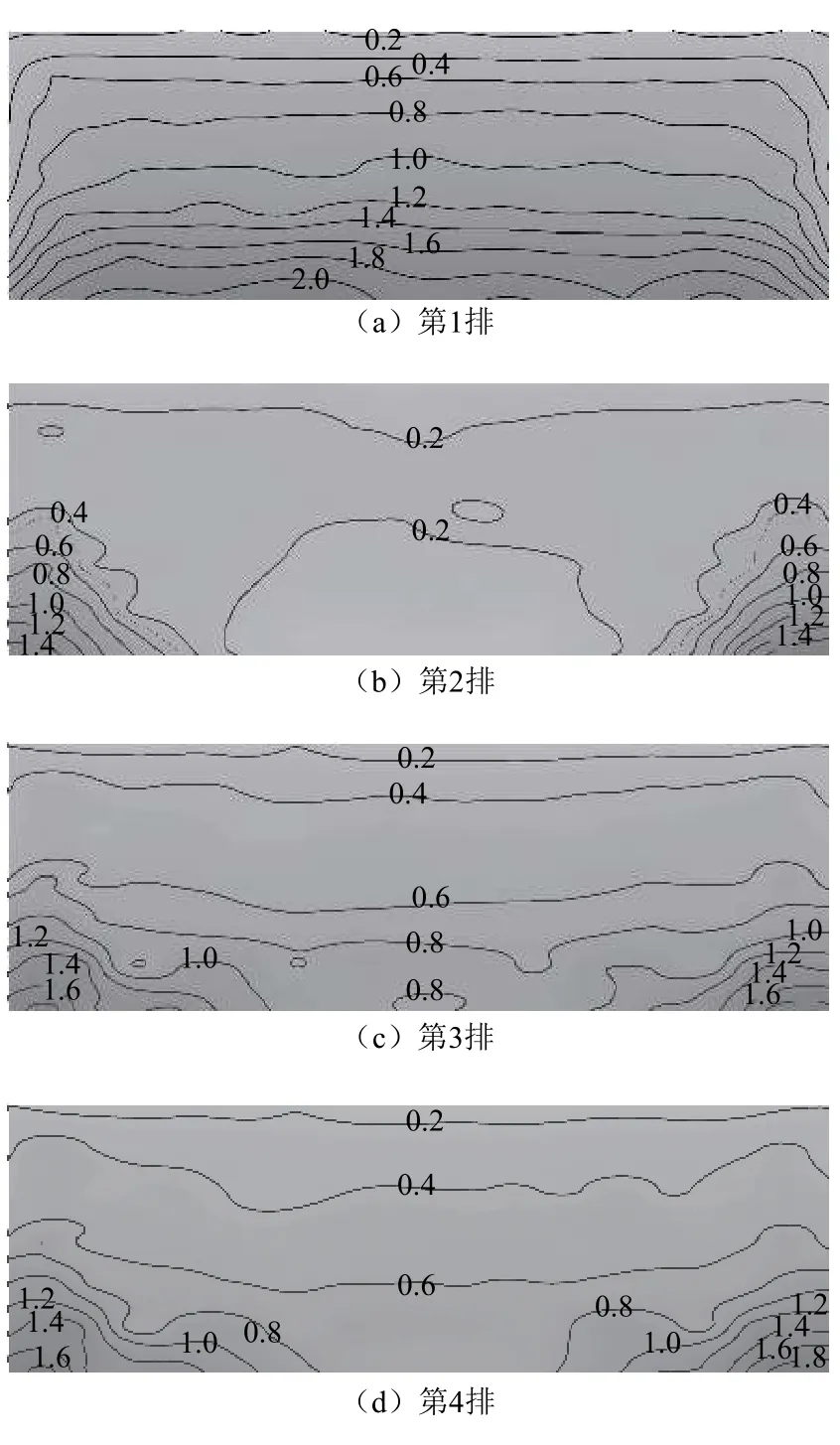
图8 光伏板体型系数分布Fig.8 Distribution of solar panels pressure coefficient

综上可知，上游光伏板对下游光伏板存在干扰效应，倾角越大，这种干扰效应越明显，随着上游光伏板数量的增加，这种干扰效应趋于稳定。

3 试验结果与规范

表1给出了光伏板体型系数试验结果与各国光伏板风荷载取值规范的比较，表中ASCE 7-10代表美国规范[16]，AN/NZS 1170代表澳洲规范[17]。当倾角β= 10°时，顺风向风荷载试验值与《光伏支架结构设计规程》相比约小56%，其余情况差距较小；与美国规范取值差距较大。当倾角β= 10°，顺风向风荷载试验值与澳洲规范值相比较小；背风向风荷载试验值与澳洲规范值相比较大。

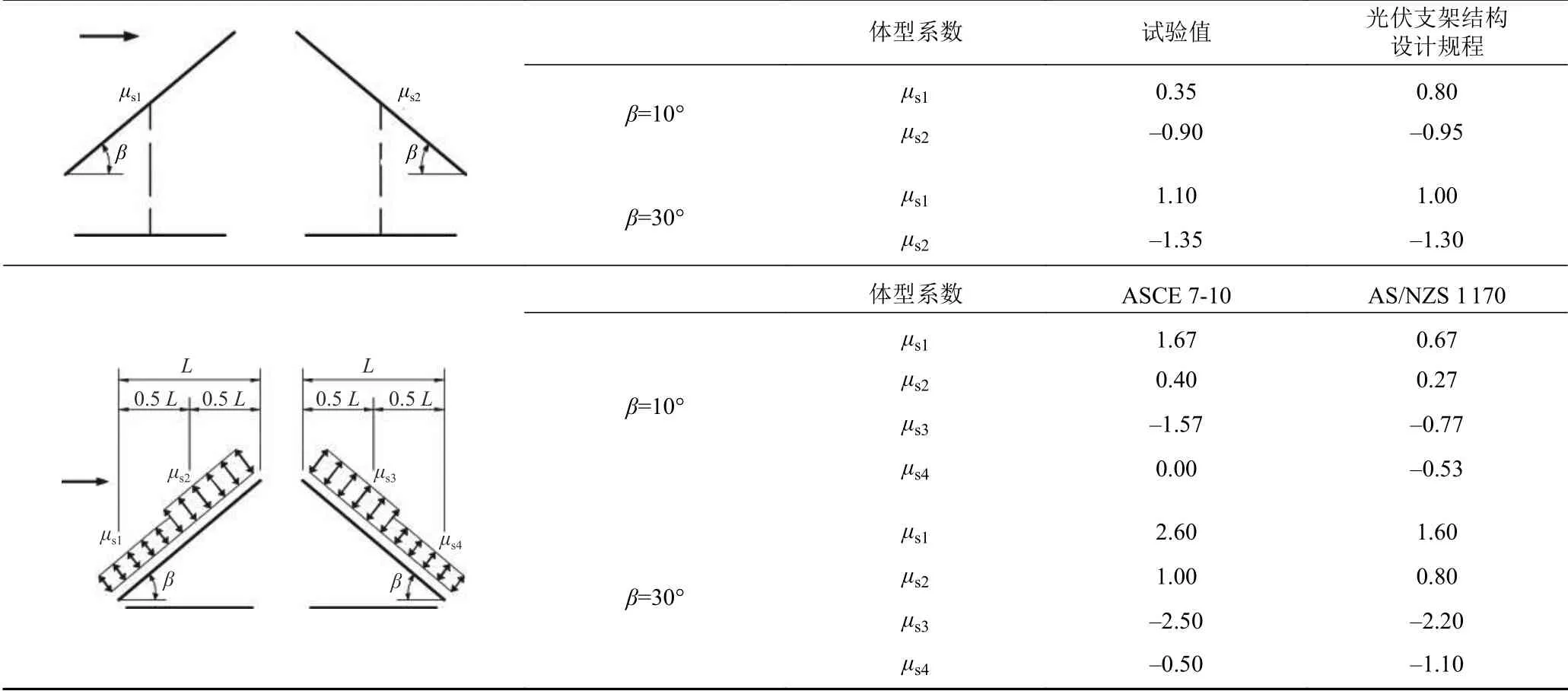
表1 光伏板体型系数试验值与规范值对比Table 1 Comparison between the test value and the standard value of the solar panel pressure coefficient

4 结 论

通过刚性模型测压风洞试验，研究了单组光伏板体型系数的变化规律，并对光伏阵列的干扰效应进行了分析，得到以下结论：

1）单组光伏板体型系数分布较为均匀，最不利风向角出现在0°和180°附近，倾角越大，光伏板体型系数也越大；同一工况下，光伏板近风端的体型系数大于远风端。根据试验结果给出光伏板体型系数：当倾角β= 10°时，正压取值为0.35，负压取值为–0.90；当倾角β= 30°时，正压取值为1.10，负压取值为–1.35。该取值与《光伏支架结构设计规程》相比，倾角β= 10°时，正压取值远小于规范的0.80，其余情况与规范差距较小。

2）在光伏阵列中，上游光伏板对下游光伏板有明显的干扰效应，使得下游光伏板所受风荷载显著减小。其中，前3排风荷载变化明显，第4排以后的风荷载取值趋于稳定。

3）板面迎风（正压）和板面背风（负压）时的折减效应不同，光伏板倾角越大，折减效应越明显。板面迎风时，正压的折减系数更小，本文10°和30°倾角对应的折减系数均小于0.5；板面背风时，负压的折减系数较大，10°和30°倾角对应的折减系数分别小于0.9和0.6。