基于充电电压片段的锂离子电池状态联合估计方法

王萍　张吉昂　程泽　于耀先

摘   要：锂离子电池的荷电状态（SOC）、健康状态（SOH）和剩余使用使命（RUL）是锂离子电池安全稳定运行的重要状态参数，本文提出一种基于充电电压上升片段的锂离子电池状态联合估计方法，实现对电池预测起点（SP）到寿命终点（EOL）的较长运行周期内SOC、SOH和RUL的联合估计. 该框架在充电阶段进行SOH和RUL估计，在放电阶段进行SOC估计. 首先提取电池恒流充电电压曲线片段的上升时间作为健康特征（HF），以HF作为输入，循环容量作为输出，建立最小二乘支持向量机（LSSVM）电池老化模型，对当前健康状态进行估计;采用等效电路模型对该电压区段进行非线性拟合，用拟合参数建立状态空间模型，结合无迹卡尔曼滤波算法进行SOC估计;用高斯过程回归时间序列模型对电池的健康特征序列进行建模，通过循环次数外推预测健康特征的变化趋势，并结合LSSVM老化模型，对RUL进行预测并给出置信区间. 实验结果表明，所提方法具有较高的估计精度和较好的稳定性.

关键词：荷电状态;健康状态;剩余使用寿命;等效电路模型;数据驱动方法

中图分类号：TM912.1                   文献标志码：A

A Coupled State Estimation Method of Lithium

Batteries Based on Partial Charging Voltage Segment

WANG Ping，ZHANG Jiang，CHENG Ze，YU Yaoxian？覮

（School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China ）

Abstract：The state of charge （SOC）， state of health （SOH） and residual mission （RUL） of lithium-ion battery are important state parameters for the safe and stable operation of lithium-ion battery. In this paper， a coupled estimation method of lithium-ion battery state based on the rising segment of charging voltage is proposed to realize the coupled estimation of SOC， SOH and RUL in a long operation cycle from the starting point of battery prediction （SP） to the end of life （EOL）. The framework estimates SOH and RUL in the charging phase and SOC in the discharge phase. Firstly， the rising time of constant current charging voltage curve segment is extracted as the health feature （HF）， and the HF as the input and cycle capacity as the output are used to establish the  least squares support vector machine （LSSVM） battery aging model for SOH estimation; The equivalent circuit model is used for nonlinear fitting of the voltage segment， and the state space model is established with the fitting parameters， which is combined with the unscented Kalman filter algorithm to estimate SOC; Gaussian process regression time series model is used to model the health feature series， and the change trend of HF is predicted by extrapolation of cycle times，which is combined with LSSVM model to predict RUL and the corresponding confidence interval. The experimental results show that the proposed method has high estimation accuracy and good stability.

Key words：state of charge;sate of health;remaining useful life;equivalent circuit model;data-driven method

鋰离子电池具有成本低、能量密度高、循环寿命长的优点，在全球能源和环境危机不断加剧的背景下，正逐渐成为电动汽车、直流变电站和光伏电网的重要储能装置[1]. 对锂离子电池配备电池管理系统（battery management system，BMS）可以对电池进行科学评估、风险预警和定期更换，保障电池的健康稳定运行. 锂离子电池的荷电状态（state of charge，SOC）、健康状态（state of health，SOH）和剩余使用寿命（remaining useful life，RUL）是BMS运维的重要参数[2]. SOC是电池短时间尺度的状态变化，其实时估计可以预测系统运行时间，制定合理的充放电策略. SOH用来描述电池在不同循环次数下的老化程度，是对长时间尺度下当前状态的描述，其准确估计有利于对电池的健康诊断，及时更换老化电池. 此两者是对电池当前状态的描述，而RUL定义为电池从当前时刻衰减至寿命终止（End of Life，EOL）所需的循环次数，是对电池未来状态的描述，其准确估计有利于合理规划电池的投运，提前排除隐患. 三者从不同方面保障系统的平稳运行.

不同于电压电流等可测参数，锂离子电池的SOC、SOH和RUL参数无法用传感器直接测量，只能根据一些外部可测量，结合数学算法进行定量估计. 电池的状态估计方法主要有间接测量法、模型法和数据驱动法等，下面分别展开介绍.

SOC估计的方法中，测量法主要是直接利用定义推出的基于电流积分的安时积分法和通过测量电池充放电过程中的开路电压进行SOC估计的开路电压法[3]，但是前者容易受到初始SOC误差的影响，且估计误差会随着时间不断积累，无法进行校正和补偿;后者需要耗费较长的时间，不适合在线使用. 数据驱动方法[4]用算法来学习电压、电流、温度等可测量与SOC的映射关系，训练量和计算量较大，不易在线应用. 模型法需要建立等效电路模型（equivalent circuit model，ECM），包含电压源、电阻电容等元件，以模拟电池的外部工作状态，并结合滤波算法进行闭环SOC估计[5]. 这种方法的稳定性较好，可以校正初值误差，避免测量误差的时间累积. 缺点是模型的阻容参数的适应性较差，随着电池老化，电池的阻容参数会发生较大变化[6]，模型参数的辨识值会产生较大的拟合误差，不适合电池全周期的SOC估计. 此外，当前可用容量或健康状态会对SOC的估计结果造成较大的影响，不宜单独进行SOC估计.

SOH估计方法中，测量法主要是通过小电流放电进行核容，精确度高但是费时费力. 基于模型的方法主要包括电化学模型和经验退化模型. 电化学模型对于电池的内部工作机理的描述更为细致，通过建立一系列的偏微分方程来描述电池的容量衰退理化机制，如基于多孔电极理论搭建的准二维多孔电极模型（pseudo two-dimensional model，P2D model）[7]及其简化方案[8]，但电化学模型参数辨识困难，方程计算复杂，不适合BMS系统的在线估计. 经验退化模型可以对电池全周期的容量衰退趋势进行建模[9]，参数辨识简单，但是难以适应电池的个体差异导致的不同容量衰退趋势，同时难以刻画锂离子电池的容量再生现象，即电池容量的局部波动，常與其他方法结合使用[10].基于数据驱动的SOH估计方法无须分析电池的内部机理，通过提取和分析与电池容量衰退密切相关的外部健康特征（health factor，HF）[11]，并通过机器学习的算法来建立HF与电池SOH之间的非线性映射关系，避免了物理建模和参数辨识问题，灵活性较强，应用广泛. 这类方法主要依赖于所选健康特征的合理性和训练算法的泛化能力[12].

RUL预测方法中的模型方法包括随机过程模型和经验退化模型，随机过程模型将锂离子电池的衰退过程看作一个随机的时间序列，对其进行建模，常见的随机过程模型包括Wiener模型[13]，马尔可夫（Markov）模型[14]，布朗运动模型[15]等，这类模型中包含随机项，每次计算结果的波动性较大;经验模型利用数学公式对电池的历史数据进行拟合建立退化模型，外推迭代模型实现对锂离子电池RUL的预测. 常见的经验模型包括指数模型[16]、多项式模型[17]和组合模型[18]等，模型方法通常只能提供点预测结果，模型跟踪能力差，在RUL长期预测中表现不佳. 基于数据驱动的RUL预测方法包括神经网络（neural network，NN）[19]、相关向量机（Relevance vector machine，RVM）[20]、高斯过程回归（Gauss process regression，GPR）[21]等. 数据驱动方法有较好的非线性建模能力，在RUL长期预测中表现良好[22]，并提供区间预测结果.

锂离子电池的状态估计研究中，对于SOC、SOH和RUL参数的单独估计最为常见[3-5，9-12，16-22]，其次是对两个参数进行联合估计，如SOC-SOH联合估计[23-24]，SOH-RUL联合估计[25-26]. 文献[23]提出一种基于粒子滤波的SOC-SOH多时间尺度估计方案;文献[24]采用动态神经网络对SOC-SOH进行闭环观测;文献[25]用布朗运动模拟电池SOH衰退时间序列，对短期SOH和长期RUL进行联合估计;文献[26]采用长短时记忆神经网络分别对SOH和RUL进行多对一和一对一映射. 但是由于SOC、SOH和RUL都是电池运行的重要参数，且三者之间也存在复杂的相互影响，伴随电池全周期运行的始终，只考虑其中的一个或部分会导致较大的估计误差. 比如电池不断老化中，电池等效模型的阻容参数会明显变化，造成SOC估计的不准确;电池的当前健康状态也影响着对电池寿命未来变化趋势的研判，影响RUL值[25]. 所以在电池较长生命周期内对SOC、SOH和RUL进行联合估计具有现实的必要性.

估计算法方面，纯模型法或者纯数据驱动法不能完全令人满意，前者的鲁棒性较好，但是无法适应电池的不断老化而自动调整;后者泛化能力较强，但比较依赖训练样本的数量和代表性. 由于电池长时间运行的数据量比较大，采用纯数据法会造成较大的计算负担，无法在线应用. 所以有必要探索两种方法的有机融合，提高联合状态估计算法的准确度和稳定性.

锂离子电池的充电电压与电池状态具有较好的联系，且容易获取，因此本文以充电电压片段为切入点，将等效电路模型（equivalent circuit model，ECM）与数据驱动（data driven method，DDM）有机融合，在锂离子电池较长生命周期内，实现SOC-SOH-RUL联合估计.

本文的创新性贡献如下：

1）利用电压片段进行电池建模和状态估计，能够适应完全充电和局部充电情形，适应直流放电和随机放电工况，计算量小，可操作性强.

2）提出了等效电路模型和数据驱动方法相融合的联合估计方案，该方案结合了模型法的稳定性和数据法的学习能力，能够在同一个框架下联合估计电池的SOC、SOH和RUL三个状态参数，估计精度高.

3）考虑了电池使用过程中状态参数的关联影响，能够实现各状态参数的长期稳定预测.

在Oxford数据集和NASA电池数据集上进行实验验证，结果表明了所提方法的可行性.

1   健康特征和等效电路模型

1.1   锂离子电池SOC、SOH和RUL定义

1.2   数据来源

1.3   健康特征提取

1.4   等效电路模型

2   相关数学方法

2.1   UKF

2.1.1   系统初始化

2.2   LSSVM和GPR算法

4   實验结果与分析

4.1   牛津数据集

4.1.1   SOH和RUL估计结果

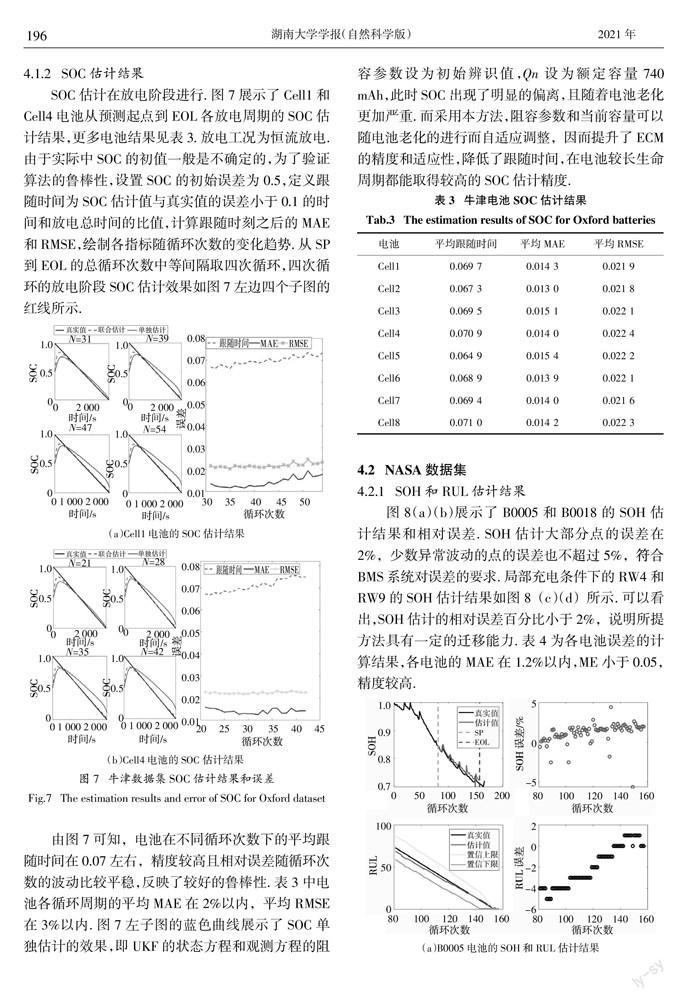
4.1.2   SOC估计结果

SOC估计在放电阶段进行. 图7展示了Cell1和Cell4电池从预测起点到EOL各放电周期的SOC估计结果，更多电池结果见表3. 放电工况为恒流放电. 由于实际中SOC的初值一般是不确定的，为了验证算法的鲁棒性，设置SOC的初始误差为0.5，定义跟随时间为SOC估计值与真实值的误差小于0.1的时间和放电总时间的比值，计算跟随时刻之后的MAE和RMSE，绘制各指标随循环次数的变化趋势. 从SP到EOL的总循环次数中等间隔取四次循环，四次循环的放电阶段SOC估计效果如图7左边四个子图的红线所示.

4.2   NASA数据集

4.2.1   SOH和RUL估计结果

4.2.2   SOC估计结果

5   结   论

本文以锂离子电池充电电压片段为切入点，进行等效电路模型建模和健康特征（HF）提取，在预测起点（SP）之前建立反映电池老化的LSSVM老化模型. SP之后循环工作时采集该压升片段，将HF代入LSSVM模型中实现SOH估计;用每次循环所建立的等效电路模型，构建SOC估计的状态空间模型，对放电的SOC进行估计;用高斯过程回归时间序列模型对健康特征序列循环次数的变化进行建模，通过循环次数外推对DV_DT的变化趋势进行预测，将变化趋势输入LSSVM老化模型中，输出SOH的退化轨迹，该轨迹与寿命阈值的交点即为RUL预测值，并给出区间预测结果. 采用Oxford和NASA数据集进行算法验证，结果表明所提方法能够在电池预测起点之后的较长运行周期内实现SOC、SOH和RUL的准确估计.

本文提出的状态联合估计方案不需要锂电池内部的电化学机理，借助电压、电流等常规物理量，通过等效电路模型和数据驱动方法的有机融合，实现了SOC、SOH和RUL的联合估计，计算量小，实用性强.

参考文献

[1]    SARMAH S B，KALITA P，GARG A，et al. A review of state of health estimation of energy storage systems：challenges and possible solutions for futuristic applications of Li-ion battery packs in electric vehicles[J]. Journal of Electrochemical Energy Conversion and Storage，2019，16（4）：.DOI：10.1115/1.4042987.

[2]    RAHIMI-EICHI H，OJHA U，BARONTI F，et al. Battery management system：an overview of its application in the smart grid and electric vehicles[J]. IEEE Industrial Electronics Magazine，2013，7（2）：4—16.

[3]    NG K S，MOO C S，CHEN Y P，et al. State-of-charge estimation for lead-acid batteries based on dynamic open-circuit voltage[C]//2008 IEEE 2nd International Power and Energy Conference. Johor Bahru，Malaysia：IEEE，2008：972—976.

[4]    DENG Z W，HU X S，LIN X K，et al. Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression[J]. Energy，2020，205：118000.

[5]    XIA B Z，SUN Z，ZHANG R F，et al. A comparative study of three improved algorithms based on particle filter algorithms in SOC estimation of lithium ion batteries[J]. Energies，2017，10（8）：1149.

[6]    WAAG W，KAEBITZ S，SAUER D U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application[J]. Applied Energy，2013，102：885—897.

[7]    DOYLE M，FULLER T F，NEWMAN J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell[J]. Journal of the Electrochemical Society，1993，140（6）：1526—1533.

[8]    PANG H，MOU L J，GUO L，et al. Parameter identification and systematic validation of an enhanced single-particle model with aging degradation physics for Li-ion batteries[J]. Electrochimica Acta，2019，307：474—487.

[9]    JIANG Y Y，ZHANG J，XIA L，et al. State of health estimation for lithium-ion battery using empirical degradation and error compensation models[J]. IEEE Access，2020，8：123858—123868.

[10]  王萍，張吉昂，程泽. 基于最小二乘支持向量机误差补偿模型的锂离子电池健康状态估计方法[J].电网技术. https：//doi.org/10.13335/j.1000—3673.pst.2021.0045.

[11]  GUO P Y，CHENG Z，YANG L. A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction[J]. Journal of Power Sources，2019，412：442—450.

[12]  YUN Z H，QIN W H，SHI W P，et al. State-of-health prediction for lithium-ion batteries based on a novel hybrid approach[J]. Energies，2020，13（18）：4858.

[13]  JIN G，MATTHEWS D E，ZHOU Z B. A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries inspacecraft[J]. Reliability Engineering & System Safety，2013，113：7—20.

[14]  PATTIPATI B，SANKAVARAM C，PATTIPATI K. System identification and estimation framework for pivotal automotive battery management system characteristics[J]. IEEE Transactions on Systems，Man，and Cybernetics，Part C （Applications and Reviews），2011，41（6）：869—884.

[15]  LONG B，XIAN W M，JIANG L，et al. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries[J]. Microelectronics Reliability，2013，53（6）：821—831.

[16]  WANG D，MIAO Q，PECHT M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model[J]. Journal of Power Sources，2013，239：253—264.

[17]  XING Y J，MA E W M，TSUI K L，et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries[J]. Microelectronics Reliability，2013，53（6）：811—820.

[18]  CHEN L，LIN W L，LI J Z，et al. Prediction of lithium-ion battery capacity with metabolic grey model[J]. Energy，2016，106：662—672.

[19]  REZVANI M，ABUALI PHD M，LEE S，et al. A comparative analysis of techniques for electric vehicle battery prognostics and health management （PHM）[C]//SAE Technical Paper Series. Warrendale，PA，United States：SAE International，2011.

[20]  LIU D T，ZHOU J B，LIAO H T，et al. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems，Man，and Cybernetics：Systems，2015，45（6）：915—928.

[21]  PATTIPATI B，SANKAVARAM C，PATTIPATI K. System identification and estimation framework for pivotal automotive battery management system characteristics[J]. IEEE Transactions on Systems，Man，and Cybernetics，Part C （Applications and Reviews），2011，41（6）：869—884.

[22]  LIU J，SAXENA A，GOEBEL K，et al. An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries[C]. Proceedings of Annual Conference of the Prognostics and Health Management Society，Portland，2010.

[23]  印學浩，宋宇晨，刘旺，等. 基于多时间尺度的锂离子电池状态联合估计[J]. 仪器仪表学报，2018，39（8）：118—126.

YIN X H，SONG Y C，LIU W，et al. Multi-scale state joint estimation for lithium-ion battery[J]. Chinese Journal of Scientific Instrument，2018，39（8）：118—126. （In Chinese）

[24]  CHE Y B，LIU Y S，CHENG Z，et al. SOC and SOH identification method of Li-ion battery based on SWPSO-DRNN[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics，2021，9（4）：4050—4061.

[25]  DONG G Z，CHEN Z H，WEI J W，et al. Battery health prognosis using Brownian motion modeling and particle filtering[J]. IEEE Transactions on Industrial Electronics，2018，65（11）：8646—8655.

[26]  LI P H，ZHANG Z J，XIONG Q Y，et al. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network[J]. Journal of Power Sources，2020，459：228069.

[27]  ABU-SHARKH S，DOERFFEL D. Rapid test and non-linear model characterisation of solid-state lithium-ion batteries[J]. Journal of Power Sources，2004，130（1/2）：266—274.

[28]  TIAN Y，XIA B Z，SUN W，et al. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter[J]. Journal of Power Sources，2014，270：619—626.1225—1236.

[29]  LIU K L，HU X S，WEI Z B，et al. Modified Gaussian process regression models for cyclic capacity prediction of lithium-ion batteries[J]. IEEE Transactions on Transportation Electrification，2019，5（4）：1225—1236.

[30]  CHEN X K，LEI H，XIONG R，et al. A novel approach to reconstruct open circuit voltage for state of charge estimation of lithium ion batteries in electric vehicles[J]. Applied Energy，2019，255：113758.

[31]  YO KOBAYASHI，HAJIME MIYASHIRO，ATSUKO YAMAZAKI，et al. Unexpect fade and recovery mechanism of LiFePO4 /graphite cells for grid operation[J]. Journal of Power Sources，2020，449：227502—227510.