再生骨料取代率对地聚物混凝土尺寸效应的影响
2021-09-14丁兆洋周静海刘爱霞
丁兆洋,周静海,苏 群,刘爱霞,王 晴
(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.沈阳城市建设学院土木工程系,辽宁 沈阳 110167;3.沈阳建筑大学材料科学与工程学院,辽宁 沈阳 110168)
地聚物是一种新型的绿色胶凝材料,主要原材料是含有硅、铝和钙成分的工业废渣(矿渣、硅灰、粉煤灰、硼泥等)[1-2],采用化学激发的方法可以使其产生力学强度。目前已经有学者研制出了抗压强度达到30~80 MPa的地聚物材料,出色的力学性能可以使地聚物成为水泥的理想替代品[3-6]。再生骨料混凝土为采用废弃的混凝土作为集料制备的混凝土,其力学性能已经得到充分的认识[7-8],目前的主要研究结论为:采用再生骨料制备混凝土及其构件会略微牺牲掉一部分强度和耐久性,但是由于采用了废弃的混凝土,其环保意义极为显著[9-10]。
地聚物再生骨料混凝土采用地聚物和再生骨料作为胶凝材料和集料,这将使得工业废渣、废弃混凝土等进行循环利用,是一种绿色环保的新型建筑材料。但是由于再生骨料与天然骨料存在差异,胶凝材料为地聚物而非传统的水泥,地聚物再生骨料混凝土的力学性能与普通混凝土的会有所差异,尤其是这种混凝土的尺寸效应方面还没有报道,这严重制约了地聚物再生骨料混凝土的应用。笔者采用碱激发工业废渣的方法制备地聚物作为胶凝材料,采用废弃混凝土作为骨料,制备地聚物再生骨料混凝土,并研究再生骨料取代率对地聚物再生骨料混凝土尺寸效应的影响。
1 试 验
1.1 试验用原材料
试验用粉煤灰为一级粉煤灰,采购自丰业粉煤灰技术开发有限公司;矿渣为高炉粒化矿渣,采购自鞍山钢铁股份有限公司,表1为粉煤灰和矿渣的主要化学成分。水玻璃选用液体水玻璃,原始模数为3.3模,水玻璃的成分及性质如表2所示。再生骨料为经人工破碎成最大粒径25 mm的废弃混凝土,砂子为中细河砂。

表1 粉煤灰和矿渣的化学组成

表2 水玻璃的化学组成
1.2 试块配比及分组
试验所用的地聚物胶凝材料采用强度最佳配合比[11],通过改变粉煤灰和矿渣的用量来调整原料中的氧化物物质的量比,使n(CaO+MgO)∶n(SiO2+Al2O3)=1;碱激发剂采用混有水玻璃的NaOH水溶液,水玻璃掺量为液体总质量的40%,NaOH的浓度为9 mol/L;砂率为0.35,试验配合比如表3所示。地聚物再生骨料混凝土制备成边长为100 mm、150 mm、200 mm的立方体试块,每种尺寸和配比的试块共做6个,共计90个试块,测试28 d龄期的抗压强度,仪器选用济南旭联仪器设备有限公司的YES-2000型混凝土抗压强度检测压力机。
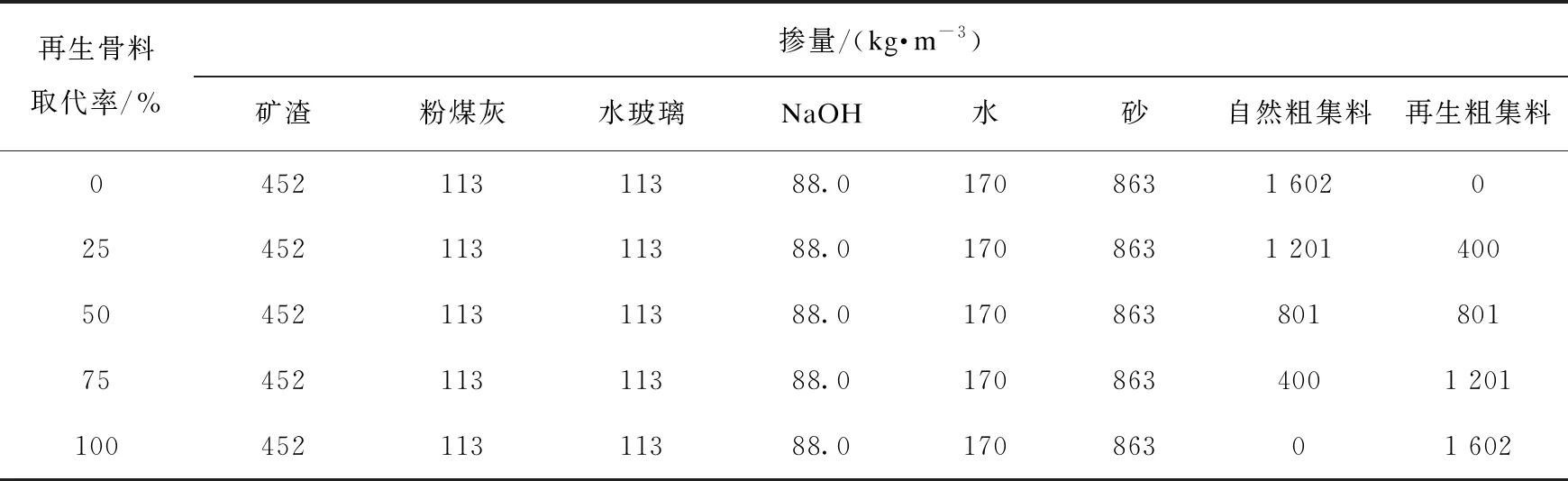
表3 地聚物再生骨料混凝土配合比
2 结果与分析
2.1 再生骨料取代率对抗压强度的影响
图1为再生骨料混凝土100 mm、150 mm、200 mm边长的立方体试块的抗压强度与再生骨料取代率的关系。由图1可知,不同边长地聚物再生骨料混凝土抗压强度的规律为:f100>f150>f200,其总体规律为试块的边长越长,抗压强度越小,其中边长为 150 mm和200 mm的立方体试块比边长为100 mm立方体试块的平均强度降低了12.62%和19.32%。所有尺寸试块都有一个统一的规律:当再生骨料取代率低于50%时,地聚物再生骨料混凝土的抗压强度与骨料取代率成正比关系;当再生骨料取代率高50%时,则成反比关系。这是由于再生骨料的旧水泥砂浆相中存在大量的孔隙,可以吸收水分。再生骨料取代率少时,自然石材为骨料主体,由于再生骨料吸收了水分,相当于降低了实际水胶比,强度高。再生骨料超过一定量时,虽然实际水胶比进一步降低,但是再生骨料自身强度低于自然石材的强度,此时再生骨料为骨料主体,混凝土的强度以再生骨料为主导,则再生骨料混凝土的强度下降。这一现象被称为强度变异现象,但是由于所选用再生骨料的吸水率、密度及旧砂浆掺量不同,导致不同研究者得出的强度变异现象的值不同。彭建庭[12]认为再生骨料掺量为30%时发生强度变异现象;肖建庄等[13]认为再生骨料掺量为50%时发生强度变异现象;孙晓雪等[14]认为再生骨料掺量为70%时发生强度变异现象。由图1可知,笔者采用的再生骨料发生强度变异现象时再生骨料的取代率为50%。
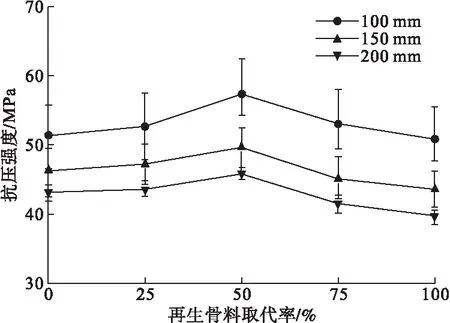
图1 不同再生骨料取代率和尺寸条件下的抗压强度
2.2 再生骨料取代率对强度标准差的影响
地聚物再生骨料混凝土的骨料为再生骨料,其内部有大量原始裂纹和薄弱且不稳定的旧砂浆相;胶凝材料为地聚物,地聚物的主要成分为工业废渣,其性能不如水泥这种工业产品稳定。再生骨料的内部缺陷以及地聚物性能的不稳定都会对地聚物再生骨料混凝土的强度产生未知的影响,从而加大强度的离散型。图2为不同尺寸地聚物再生骨料混凝土抗压强度的强度标准差σ。σ值越大,混凝土强度的离散程度越大,现行国家标准《混凝土强度检验评定标准》(GB50107—2010)规定,对于强度等级C20以上的混凝土,σ≤3.5为优秀,3.5≤σ≤5为一般,σ>5为差。从图2中可以看出,试块边长为200 mm的地聚物再生骨料混凝土的σ都远小于3.5;试块边长为150 mm的地聚物再生骨料混凝土的σ在3.5左右,其平均值略高于3.5;试块边长为100 mm的地聚物再生骨料混凝土的σ都略高于5。说明边长越大,地聚物再生骨料混凝土立方体试块抗压强度的离散程度越小,而且只有当边长为200 mm时,地聚物再生骨料混凝土抗压强度的离散程度才为优秀;当边长为150 mm时,其抗压强度的离散程度为一般,也可以使用;当试块边长为100 mm时,其抗压强度离散性太大,不适合使用。

图2 不同再生骨料取代率和尺寸条件下的地聚物再生骨料混凝土强度标准差
2.3 再生骨料取代率对换算系数的影响
标准尺寸试块与非标准尺寸试块间抗压强度值可采用尺寸换算系数α来换算。现行国家标准《普通混凝土力学性能试验方法标准》(GB/T 50081—2019)中规定标准试块的尺寸为边长150 mm的立方体试块,其他尺寸立方体试块的换算系数为
α100=fcu,100/fcu,150.
(1)
α200=fcu,200/fcu,150.
(2)
式中:fcu,100、fcu,150、fcu,200为边长100 mm、150 mm、200 mm的立方体试块抗压强度。
图3为再生骨料取代率与尺寸换算系数的关系。根据国家现行标准《普通混凝土力学性能试验方法标准》(GB/T 50081—2019)中规定,边长为200 mm立方体试块的尺寸换算系数为1.05,边长为100 mm立方体的尺寸换算系数为0.95,图3中虚线所示。图3中不同边长的地聚物再生骨料混凝土抗压强度尺寸换算系数都不在在0.95~1.05内,且边长为200 mm立方体试块尺寸换算系数平均值为0.923;边长为100 mm立方体试块为1.145,说明地聚物再生骨料混凝土的尺寸换算系数不能参考普通水泥混凝土的标准。其原因与上一节抗压强度离散性的分析一致,即地聚物胶凝材料和再生骨料的性能的都与水泥和自然石材不同,使其制备的混凝土也无法按照普通混凝土的相关标准进行限定。通过线性拟合的方法,得出地聚物再生骨料混凝土尺寸换算系数α与再生骨料取代率ε的关系:α200=0.931-0.016×ε,α100=1.108 6-0.072 8×ε。

图3 再生骨料取代率对尺寸换算系数的影响
2.4 Bazant尺寸效应拟合
由于地聚物再生骨料混凝土是一种脆性材料,根据Bazant的尺寸效应理论[15],在荷载作用下裂缝扩展释放的应变能导致尺寸效应的存在,其名义抗压强度fN与尺寸D之间的关系:
(3)
式中:f∞为地聚物再生骨料混凝土尺寸无限大的名义抗压强度;Db为边界层开裂有效厚度。
(4)
令:X=1/D,Y=fN,C=f∞,A=f∞×Db,则式(4)可变成线性方程:
Y=AX+C.
(5)
X和Y均由试验得到的强度和试块尺寸直接计算得出,带入式(5)可以求出A和C,最后得到尺寸效应的理论公式参数(见表4)。采用表4中的数据可以得出各尺寸的地聚物再生骨料混凝土实测强度值与Bazant理论曲线的对比图(见图4)。在不同的再生骨料取代率条件下,其抗压强度实测值都在理论曲线上,说明地聚物再生骨料混凝土抗压强度可以用Bazant理论进行计算。

表4 尺寸效应理论公式参数计算
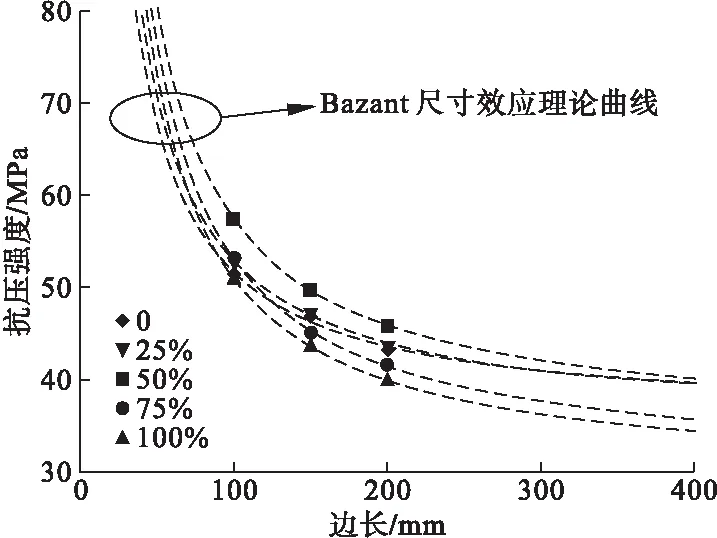
图4 实测强度值与Bazant理论强度的对比图
2.5 临界尺寸与临界强度
首先将尺寸效应相关数据进行无量纲化处理[15]:
(6)
式中:f150为边长150 mm立方体试块的地聚物再生混凝土实测强度;b为方程的待定系数。
将不同边长立方体试块的抗压强度特征值数据带入式(6)进行数学回归分析,可解出无量纲方程的相关待定系数:
(7)
再生骨料取代率与Bazant理论曲线的无量纲关系如图5所示。

图5 无量纲强度与Bazant理论强度的对比图
由图5可以看出,立方体试块边长为200 mm时,各个再生骨料取代率的尺寸都贴近理论曲线。边长为100 mm时,尺寸效应略微明显,再生骨料取代率为50%的情况下,最贴近理论曲线;再生骨料取代率0,25%,小于50%的情况下,尺寸效应负偏离于理论曲线;再生骨料取代率75%,100%,大于50%的情况下,尺寸效应正偏离于理论曲线。因此,可以判断再生骨料取代率为50%是尺寸效应变化的分界点,提出采用分段函数的方式拟合再生骨料取代率ε与f∞/f150和Db关系的方法。图6为再生骨料取代率与f∞/f150和Db关系示意图。式(8)~式(11)为拟合曲线式。

图6 再生骨料取代率与f∞/f150和Db的关系
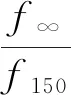
0≤ε≤50.
(8)
Db=42.840 2+0.488 0×ε,
0≤ε≤50.
(9)
50%≤ε≤100%.
(10)
Db=58.168 3+0.181 4×ε,
50%≤ε≤100%.
(11)
可以看出,对于再生骨料取代率与f∞/f150和Db关系提出的分段函数具有较高的适用性,由此将式(8)-式(11)分别代入式(6),可以得到尺寸效应与再生骨料取代率交互作用下的地聚物再生骨料混凝土名义抗压强度的预测方程:
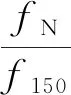
(12)
50%≤ε≤100%.
(13)
根据式(12)和式(13)可以推算出不同取代率条件下地聚物再生骨料混凝土试块尺寸无限大时的临界强度特征值fcr。考虑工程尺寸效应的适用范围,当名义抗压强度与临界尺寸特征值相差5%之内时,可以认为该名义抗压强度对应的试块的尺寸为临界尺寸Dcr,再生骨料取代率与地聚物再生骨料混凝土临界尺寸和临界强度关系如图7所示。可以看出随着再生骨料取代率的增加,临界尺寸逐渐增大,但是临界强度并不与再生骨料取代率成正比,而是当再生骨料取代率为50%时出现了最值,这与笔者对地聚物再生骨料混凝土抗压强度的分析结果一致。
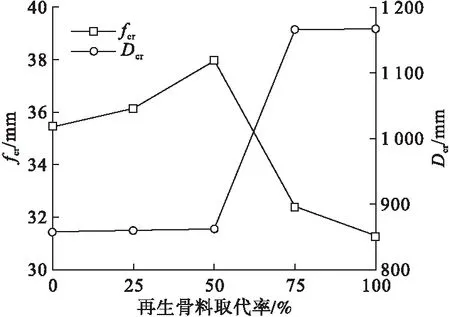
图7 临界强度和临界尺寸的关系
式(12)和式(13)综合考虑了尺寸效应与再生骨料取代率交互作用的影响,可以更加准确计算出不同再生骨料取代率条件下地聚物再生骨料混凝土的临界尺寸和临界强度值,而且采用无量纲的方法对于预测其他强度等级的抗压强度具有一定的参考。
4 结 论
(1)由于存在强度变异现象,再生骨料取代率为50%时各个尺寸试块的地聚物再生骨料混凝土抗压强度出现最大值。不同尺寸的地聚物再生骨料混凝土抗压强度规律为:f100>f150>f200。
(2)地聚物再生骨料混凝土的换算系数不能采用现行国家标准《普通混凝土力学性能试验方法标准》(GB/T50081—2019)中的换算系数。采用数学拟合方法给出骨料掺量与地尺寸换算系数的关系:α200=0.931-0.016×ε,α100=1.108 6-0.072 8×ε。
(3)边长为200 mm、150 mm和100 mm的地聚物再生骨料混凝土立方体抗压强度均符合Bazant的尺寸效应理论曲线,并得出了不同再生骨料取代率条件下的临界强度值和临界尺寸值。
