风荷载作用下超高层建筑脚手架立杆稳定性研究
2021-09-14贾世龙陈凯荟陈忠良
贾世龙,陈凯荟,2,刘 莉,陈忠良
(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.天友建筑设计股份有限公司结构设计部,天津 300384;3.沈阳万科企业有限公司工程部,辽宁 沈阳 110166)
作业平台、承重支撑架体系等临时结构直接影响超高层建筑的施工安全。K.Ohdo等[1]调查发现约10%的脚手架事故是由风引发的。对于不同工况下,支设基准面高度在100 m级以上的脚手架,架体的水平位移远远大于竖向位移,架体稳定性主要取决于风荷载[2]。因此,研究风荷载对超高层建筑脚手架的稳定性影响具有重要的工程意义。
国内外大量研究者针对风荷载对超高层建筑脚手架的稳定性影响进行了研究。S.Charuvisi等[3]研究了不同体型脚手架的风压特性,揭示架体宽度对风压系数的影响、建筑物开口形式对风压值的影响;S.Huang等[4],A.Giannoulis等[5],S.D.Amoroso等[6]利用CFD法和风洞试验得到了整体提升架体的风荷载,提出覆盖安全网脚手架的风压计算方法。H.Irtaza等[7-8]通过全尺寸的脚手架模型风洞试验,指出英美等国技术标准中的风载压力系数适用于脚手架迎风面,背风面仅做参考;秦桂娟等[9]通过现场试验和有限元分析,明确不同搭设基准高度风荷载对脚手架立杆最大弯矩值的影响,指出某些情况下现行规范中计算公式安全储备不足,建议进一步计算风荷载引起的超高层脚手架立杆的最大弯矩;王朝晖等[10]建议对规范中立杆计算长度系数进行调整。
目前,高空风振对临时结构稳定性影响效应定量分析的相关研究仍较为缺乏,现行规范也未提出相关的设计依据。基于此,笔者以超高层建筑脚手架为研究对象,基于风振理论,对高空风荷载对脚手架立杆稳定性的影响进行数值模拟研究,探究支设基准面高度、搭设方式对脚手架立杆附加轴力的影响幅度及变化规律,并优化风荷载计算公式,简化风荷载计算方法,为同类工程设计提供参考。
1 高空风荷载的确定
目前,依据我国现行规范[11-12]在100 m以内的建筑及临时结构设计中,将风荷载视为低空静力荷载,弱化风振影响,简化风振系数为1.0。风荷载按照式(1)计算:
wk=μs·μz·w0.
(1)
式中:wk、w0分别为风压标准值及风荷载基本风压值,kN /m2;μs为风荷载体形系数值;μz为风压高度变化值。
1.1 高空风荷载的特性
不同于近地风,高空风随时间的变化更为随机和频繁,其特性受到平均风特性和脉动风特性的共同影响。高空风荷载对建筑结构的影响,除了高度对平均风速的增加外,由脉动风产生的动力荷载作用效果进一步显现。
脉动风特性表现:高度越低,湍流强度越大;湍流积分尺度越大,湍流影响越显著;顺向湍流的影响效果远高于垂直向湍流和横向湍流[13-15]。
1.2 高空风荷载的计算与简化
在超高层建筑脚手架(支设基准面与地面高差大于100 m的各种脚手架)的结构抗风研究中,应充分考虑高空风荷载作用。
笔者采用等效风振力法,以顺向湍流影响为主,将脉冲风作用简化为风振系数,并叠加平均风压[16],计算超高层脚手架风荷载,将动力学问题转化为任意时刻的静力问题。根据静力学原理,产生该响应的荷载可表示为
(2)
式中:Peq(t)为等效风振力,包含气动力以及风振引起的惯性力、阻尼力在内的一种等效力;ωj为等效风振力均方根;M为结构质量分布阵;φj为结构各阶振型。
高层及超高层建筑振动均以一阶振型为主,等效静力法采用平均值与结构一阶等效风振力组合出等效静力风荷载。因此,超高层脚手架计算风荷载时需考虑风振系数,将脉冲风与平均风组合,根据规范[17],按照式(3)计算风荷载:
wk=βz·μz·μs·w0.
(3)
风振系数按照式(4)计算:
(4)
式中:g为峰值因子,取2.5;I10为10 m高处湍流强度;Bz为脉动风荷载共振分量因子;R为脉动风荷载背景分量因子。
脉动风荷载共振分量因子Bz按照式(5)进行计算:
Bz=kHa1ρxρzφ1(z)/μz.
(5)
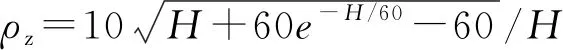
脉动风荷载背景分量因子R按照式(6)进行计算:
(6)
(7)
式中:f1为结构第一阶自振频率,Hz;kw为地面粗糙度修正系数,对应四类地面分别取1.28、1.0、0.54、0.26;ξ1为结构阻尼比,钢结构取值0.02,混凝土结构取值为0.05,笔者取值0.02。
参照高耸建筑第一阶自振频率,f1按照式(8)计算:
(8)
对钢筋混凝土结构可取0.007,钢结构可取0.013,笔者取0.013。
综上,将各式代入式(3)中,即可得到基于简化风振法计算法,水平风荷载及竖向风荷载共同作用下四类地面高空风荷载标准值,与规范计算法比较,其计算误差在7%以内。
2 风荷载附加轴力对架体稳定性的影响
对于普通脚手架设计,现行规范[12]未考虑高空风荷载对立杆轴力的影响。超高层脚手架,风荷载对立杆会进一步产生附加轴力,安装在外立杆的安全网、挡脚板、防护栏杆等配件有利于迎风面架体稳定。因此,笔者以背风面为对象,研究风荷载附加轴力值,按式(9)计算超高层脚手架立杆轴力值:
N=γG×(∑NG1k+∑NG2k)+γQ×(∑NQk+∑NQkf)×0.9.
(9)
式中:γG、γQ分别为永久荷载、可变荷载分项系数,根据《建筑结构可靠性设计统一标准》(GB50068—2018)分别取1.3和1.5;NG1k、NG2k、NQk分别为脚手架的结构自重、构配件结构、施工荷载产生的轴力设计标准值。0.9为荷载组合值系数;NQkf为风荷载附加轴力标准值。
2.1 有限元模型选择
脚手架采用扣件式钢管脚手架,脚手管为Φ48.3×3.6的Q235级钢,钢管间的连接为半刚性连接。建模过程中架体立杆及纵横向水平杆选择Beam188单元,弹性模量E=2.06×105MPa,泊松比v=0.3,剪刀撑选择Link180单元,采用Combin14弹簧单元模拟脚手架节点的半刚性连接。根据规范[17],将弹簧的转动刚度取值为35(kN·m)/rad。利用有限元ANSYS软件建立步距1.8 m,跨距1.5 m,横距1.05 m的脚手架有限元模型,连墙件采用两步两跨菱形布置形式。有限元模型图如图1所示。

图1 有限元模型图
设置考虑风荷载和未考虑风荷载两种加载方式,脚手架所在高度为150 m处有限元荷载情况及计算结果如图2、图3所示。

图2 未考虑风荷载模型图
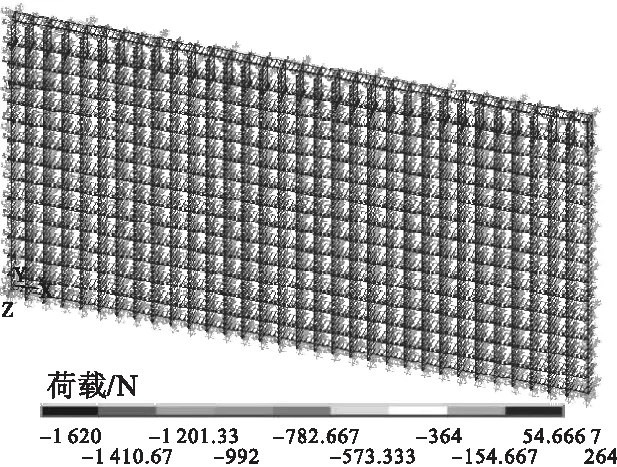
图3 考虑风荷载模型图
两种加载方式有限元分析结果如图4、图5所示。

图4 未考虑风荷载结果分析

图5 风荷载产生附加轴力值分析图
根据有限元分析结果发现,在施工荷载和风荷载共同作用下,架体底部立杆最大轴力值出现在靠近架体边缘外立杆,单元号为8 563的位置处。由于风荷载的作用,架体底部立杆最大轴力值由-7 862 N增大到-9 797 N,风荷载对底部立杆产生的附加轴力值大小为1 935 N,按照如下方法计算立杆轴力设计值,与规范计算值进行对比分析。
依据规范法,单立杆轴向力设计值,应按照以下公式计算得:
N=1.3(NG1k+NG2k)+1.5∑NQk=1.3×(3.95+4.37)+1.5×2.7=14.87 kN。
考虑风荷载附加轴力值,单立杆轴向力设计值计算如下:
N=1.3×(∑NG1k+∑NG2k)+1.5×(∑NQk+∑NQkf)×0.9=1.3×(3.95+4.37)+
1.5×(2.7+1.94)×0.9=17.07 kN。
与普通脚手架立杆轴力相比较,组合风荷载附加轴力后,立杆轴力设计值增加近15%,为进一步探究风荷载对轴力设计值的影响,笔者将针对不同搭设方案及不同高度处的超高层脚手架展开进一步研究。
2.2 不同纵距下附加轴力对架体稳定性的影响
为便于进行数据对比,依据规范[12],笔者构建la分别为1 m、1.2 m、1.5 m、1.6 m,lb为1.05 m,h为1.8 m的四种架体有限元模型(为增加架体平面刚度,连墙件采取两跨两步布置),分析搭设基准面高度为150 m的架体内力,结果如图6~图9所示。

图6 la=1 m有限元分析结果
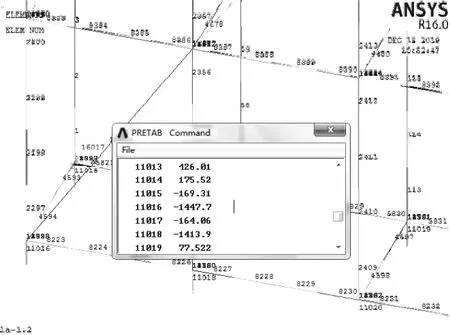
图7 la=1.2 m有限元分析结果

图8 la=1.5 m有限元分析结果

图9 la=1.6 m有限元分析结果
脚手架立杆纵距不同时,不同高度处附加轴力值及立杆轴力值与脚手架规范对比情况如表1~表4及图10、图11所示。

表1 底部立杆轴力设计值对比(la=1 m)
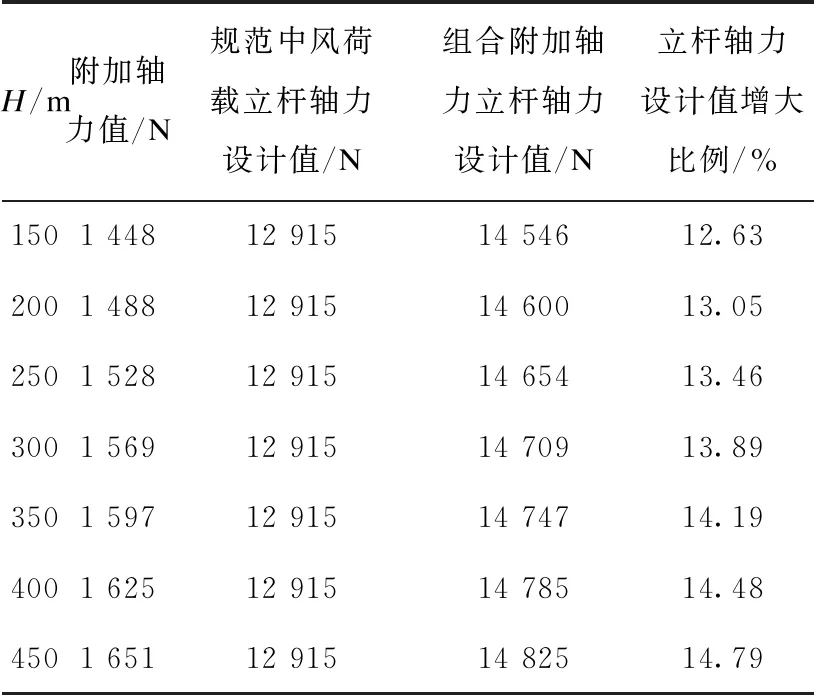
表2 底部立杆轴力设计值对比(la=1.2 m)
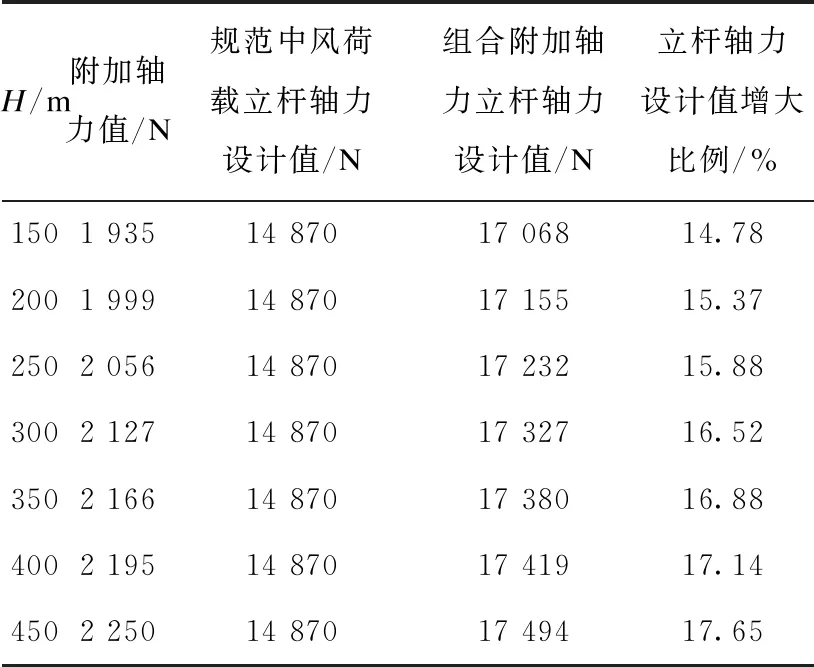
表3 底部立杆轴力设计值对比(la=1.5 m)
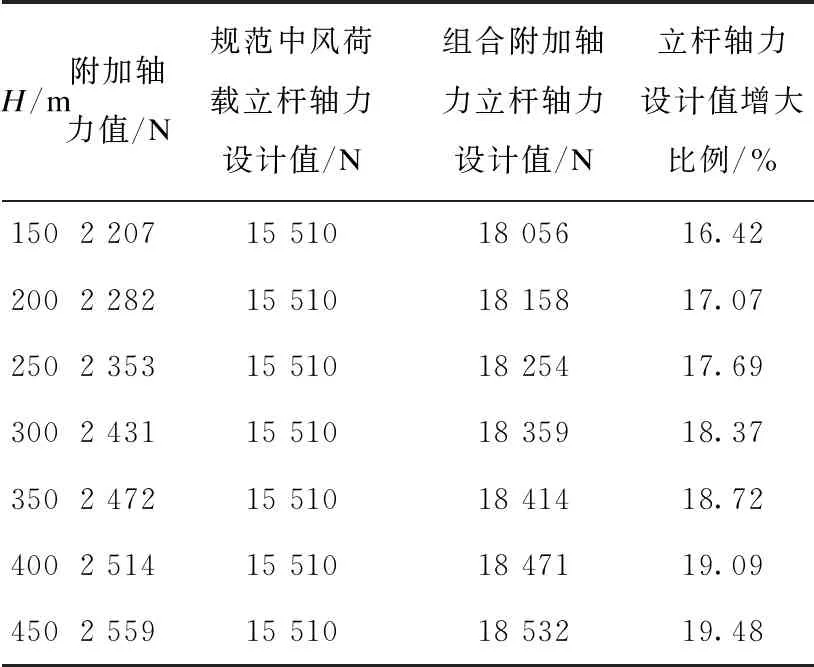
表4 底部立杆轴力设计值对比(la=1.6 m)

图10 不同纵距下附加轴力随搭设基准高度变化

图11 不同高度附加轴力随纵距变化
不同立杆纵距时,脚手架底部立杆最大轴力值均出现在靠近边缘的外立杆处,将有限元分析结果进行汇总,由表1~表4及图10可知,附加轴力值随架体支设基准面的增加而增加,附加轴力随纵距变化基本呈线性变化,每隔50 m附加轴力变化幅度随立杆纵距的增加而增加,立杆纵距为1.6 m时增加约1.95%,立杆纵距为1m时增大约1.33%。
由表1~表4及图11可知,相同支设基准面,附加轴力随立杆纵距增加而增加,但增长幅度有所不同,立杆纵距为1.5~1.6 m时的增加幅度最大,纵距每增加0.1 m附加轴力增长14.19%;纵距为1.2~1.5 m时附加轴力增加幅度小于1.0~1.2 m时的增加幅度,附加轴力随支设基准面为非线性变化。
与普通脚手架计算方法相对比,考虑附加轴力后,超高层脚手架立杆轴力均有所增加。其增大幅度随脚手架所在高度及纵距的增加而增加,立杆纵距为1.6 m时增大百分数为19.48%,立杆纵距为1m时最小增大百分数为10.06%。
2.3 不同横距下附加轴力对架体稳定性的影响
依据规范[12],笔者构建了lb分别为1 m、1.2 m、1.5 m、1.6 m,la为1.5 m,h为1.8 m的4种架体有限元模型(连墙件采取两跨两步布置),分析搭设基准面高度为150 m的架体内力,计算结构如图12~图15所示。

图12 lb=0.8 m有限元分析结果

图13 lb=0.9 m有限元分析结果

图14 lb=1.0 m有限元分析结果

图15 lb=1.2 m有限元分析结果
底部立杆最大附加轴力值均出现在边跨处内立杆,单元号为8 563的位置。架体所在不同高度处附加轴力值、立杆轴力设计值变化情况汇总如表5~表8,及图16、图17所示。
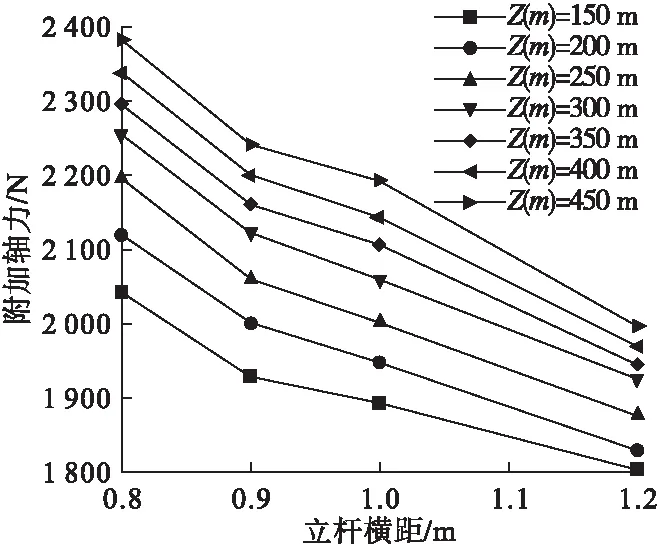
图17 不同高度附加轴力随横距变化
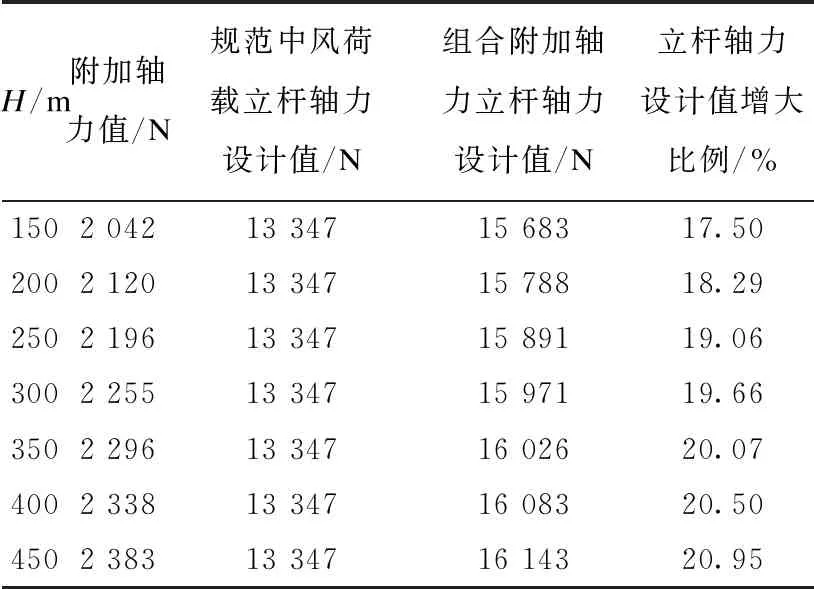
表5 底部立杆轴力设计值对比(lb=0.8 m)

表6 底部立杆轴力设计值对比(lb=0.9 m)
将有限元分析结果进行汇总,由表5~表8及图16可知:立杆横距为1.2 m时,附加轴力随脚手架所在高度的变化非线性比较明显;立杆轴力为0.8 m、0.9 m、1 m时附加轴力基本随支设基准面变化基本呈线性变化,每隔50 m附加轴力变化幅度随立杆横距的增加而降低,立杆横距为0.8 m时增加百分数约为2.76%,立杆纵距为1.2 m时增大百分数约为1.92%。
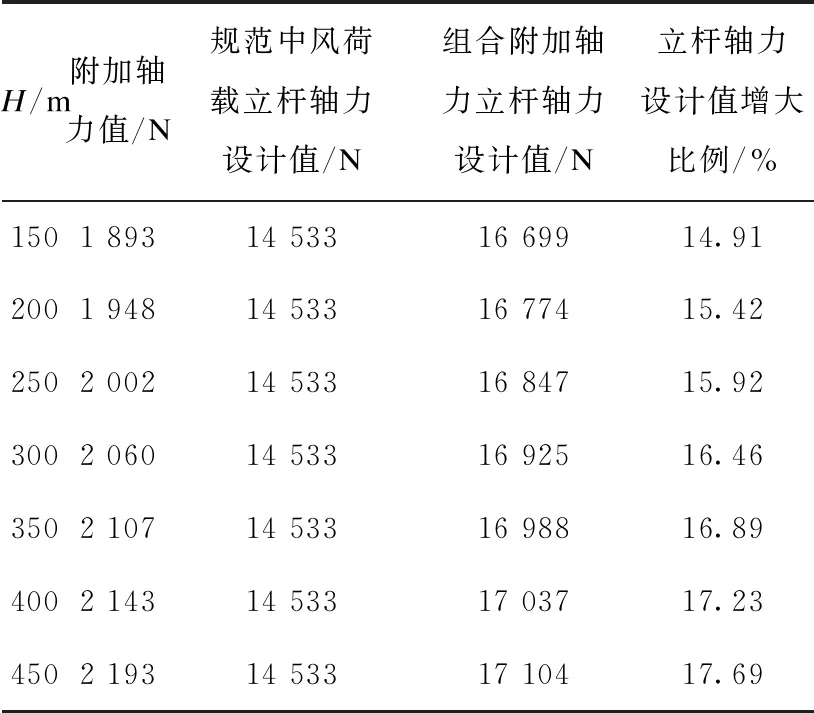
表7 底部立杆轴力设计值对比(lb=1.0 m)
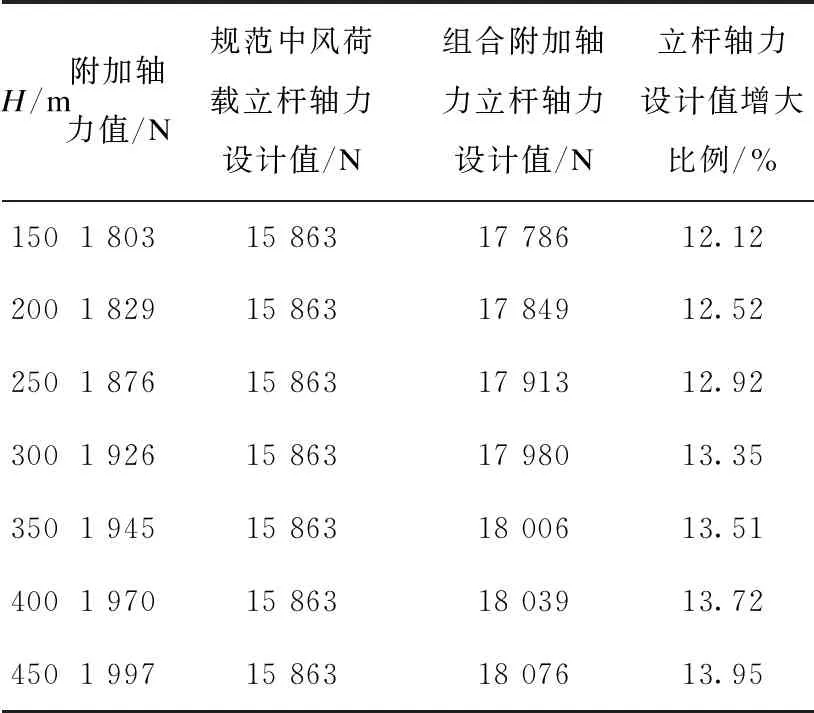
表8 底部立杆轴力设计值对比表(lb=1.2 m)

图16 不同横距下附加轴力随搭设基准高度变化
由表5~表8及图17可知,相同支设基准面,附加轴力随立杆横距增加而降低,但变化幅度呈现非线性,立杆横距为0.8~0.9 m时的变化幅度最大,横距每增加0.1 m附加轴力降低5.83%;横距为0.9~1 m时附加轴力变化幅度小于1.0~1.2 m时的变化幅度。高空风荷载对立杆的附加轴力立杆横距为0.8 m时最大增大百分数为20.95%,立杆横距为1.2 m时最小增大百分数为12.12%。
综上所述,对超高层脚手架而言,风荷载对脚手架立杆轴力的影响是显著的。附加轴力值与支设基准面高度呈正相关,随基准面高度的增加而增加;附加轴力值与立杆横距呈逆相关,随横距的增加而减小。不同构造的架体,立杆附加轴力至少增加10%,故建议计算超高层脚手架轴力设计值时将风荷载附加轴力值组合到计算公式当中。
3 结 论
(1)通过有限元计算分析,风荷载会对超高层建筑脚手架立杆产生附加轴力,其大小随支设基准面的升高而增大;当支设基准面高度超过150 m时,作用效果尤为明显;相同支设基准面,附加力增长幅度随立杆纵距的增加而增加;随立杆横距的增加而降低,其增值幅度均表现出非线性规律;对于不同搭设方式,立杆附加轴力值增幅在10%以上。
(2)采用风振系数的等效计算,提出了四类地面粗糙度风荷载简化计算公式和风荷载附加轴力计算公式,均以沈阳地区10年重现期的基本风压为依据;而对于东南沿海、西北高原地区,应进一步以实测数据做校核。
(3)对超高层建筑脚手架,高空风荷载不仅仅增加了立杆轴力,其风压变化所产生的水平弯矩将进一步增加脚手架(尤其是超高层悬挑式脚手架)的挠度变形;在实际工程设计中,应充分考虑脉动风作用,加强构造措施,以保证架体安全性、稳定性、可靠性。
