冲孔桩关乎成孔效率上限的提钻高度计算
2021-09-14范旭红薛颖楠任冠宇
范旭红,薛颖楠,杨 帆,任冠宇
(1.江苏大学土木工程与力学学院,江苏 镇江 212013;2.中国二十冶集团有限公司,上海 201900)
冲击成孔是钻孔灌注桩的重要成孔工艺,广泛适用于黏土层、碎石土层、砾卵石层、裂隙发育地层等各类地质环境,应用前景广阔[1]。冲击成孔灌注桩是采用现场钻孔然后灌注混凝土来实现的,其施工效率主要取决于成孔效率[2]。目前有关成孔效率的研究多是从施工工艺把控及病害预防角度得到的定性结论[3-7],也有学者尝试改变钻头结构来提高破岩效率从而提高成孔效率[8-10],但针对成孔过程中触底动能源头输入的研究还不多见。
冲击钻锤头通过钻机的悬吊获得势能,而后在泥浆中自由落体,受到设备阻力和泥浆阻力的影响耗散掉一部分的能量,另一部分能量转化为锤头的触底动能,进行破岩挤土形成桩孔。单次冲击时触底动能的大小决定了破岩挤土的程度,由提钻高度决定的锤头势能是冲击过程的唯一动能输入,直接影响着成孔效率。当然在成孔过程中还必须确保孔壁处于稳定状态,在孔壁稳定前提下的最大成孔速度就是成孔效率上限。
随着科技的高速发展,计算机技术也越发的普及,一些实际问题的演化结果也可以使用有限元分析软件进行模拟得到直观的结果[11-13],但目前针对冲击作用过程的模拟研究还不多见。王晓辉[14]采用ABAQUS的显式动力学方法针对球体入水过程进行了模拟,笔者也基于此种方法分析冲击锤头在泥浆中的下落过程,得到了锤头的运动时程关系,并以此为依据得到了单次冲击时的最佳提钻高度,极具工程应用价值。
1 锤头收尾速度及影响因素
在冲击成孔灌注桩中,通常采用泥浆护壁的方式来保持孔壁的稳定性,锤头由重力势能转化为触底动能的过程中,需要克服泥浆阻力做功,泥浆阻力与锤头速度有关,速度越大阻力越大[15],假设锤头在泥浆中受到的阻力为Fs,且Fs=kv,其中k为泥浆阻力系数,由牛顿第二定律可知:
(1)
对式(1)变形可得:
(2)
锤头的自由落体过程中,初速度为0,假设t时刻的速度为vt,对式(2)左右两边积分得:
(3)
对式(3)求积分并取对数后可得到泥浆中锤头运动速率与时间的关系:
(4)
随着时间增加,泥浆的阻力也增大,加速度逐渐减小,当t→+∞时,锤头的加速度为零。此时,锤头的运动由加速度减小的加速下落运动转变成匀速下落运动,锤头受到的阻力最大,与重力大小相等方向相反,合力为零。由此可推测,若锤头加速度刚达到0即刚开始做匀速直线运动时触底,就能在最短的时间内得到最大的冲击动能。为探究锤头在泥浆中的运动情况,采用有限元软件ABAQUS进行模拟分析。
并且由式(4)可知,影响锤头收尾速度的两个主要参数为锤头质量和泥浆阻力(由于机械的不断改良,设备阻力可忽略不计)。锤头质量通常与锤头的大小即锤头直径、高度有关;泥浆阻力与泥浆性能有关,也与锤头四周的泄浆孔大小有关[16]。参照《公路桥涵施工技术规范》(JTG/T 3650—2020)[17]有关泥浆性能指标的描述,取泥浆相对密度及黏度这两个会影响锤头下落速度的直接相关指标,在采用ABAQUS模拟时通过调整直接相关指标控制泥浆工况。
2 锤头下落的ABAQUS模拟
在工程中,对于土质坚硬且地质条件较好的地层,为提高成孔效率,多采用增加提钻高度的方式来提高锤头的冲击能,而现场及室内试验由于费用大、试验条件复杂而得不到普遍应用,因此其提钻高度完全依赖于工程经验总结。随着计算机技术的发展,越来越多的复杂工程可利用计算机求解,ABAQUS的显示求解器可有效解决冲击等运动事件,特别是能够解决庞大复杂的问题和模拟高度非线性问题,应用范围广泛。
2.1 模型设置
ABAQUS中常用的两种物质在空间中运动的表达方法为拉格朗日描述及欧拉描述。拉格朗日描述是一种物质描述,研究质点物理量(U/E/S)随时间的变化规律,多用于固体;欧拉描述是一种空间描述,物质在固定的框架(欧拉网格)下流动,研究空间点的物理量(P/N/T)随时间的变化规律,多用于流体[18]。泥浆作为液体可流动材料,在ABAQUS中考虑采用欧拉分析的方式,而冲锤作为固体采用拉格朗日单元,冲锤在泥浆中下落可以采用耦合的欧拉—拉格朗日分析方法,通常称之为CEL(Coupled Eulerian-Lagrangian)分析。
2.1.1 泥浆模型建立
泥浆通常被认为是宾汉流体,只有当切应力超过一个最小剪应力τ0的临界值才发生剪切变形,且切应力随剪切变形速率呈现线性变化,即在流动时保持恒定黏度,是一种典型的非牛顿流体。ABAQUS不能直接定义宾汉流体,但存在一个更广义的Herschel-Bulkley-Model(赫巴模型),可以用来定义宾汉流体的剪切黏度[19]。Herschel-Bulkley流变模式的本构方程见式(5),根据参数取值不同,它能统一表示牛顿、宾汉、指数流变模式的特性,该方程准确性高、适用范围广,广泛适用于泥浆及水泥浆。
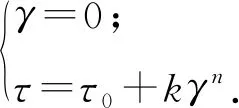
(5)
式中:τ0为屈服应力,Pa;k为稠度系数,Pa·sn;γ为剪切率,s-1;n为流变指数,无量纲。当模型中的流变指数n=1时,Herschel-Bulkley模型退化为Bingham模型,与状态方程(EOS)中描述的材料配合使用,即可准确描述泥浆的流动行为。参考工程经验,泥浆参数取值见表1。

表1 泥浆模拟参数
2.1.2 锤头模型建立
考虑到工程实际,锤头以洛阳锤为原型设计,锤头参数见表2。锤头在下落过程中形状和大小保持不变,且不产生形变,可近似看做刚体,在赋予材料属性后,通过Ridid Body将整个锤头的运动强制约束到一个参考点上,用参考点的速度及位移表达整个锤头的运动状态。

表2 锤头模型参数
2.1.3 土体模型建立
锤头下落过程中的外力只来自泥浆阻力,锤头不与孔壁土体直接接触,土体类型对锤头下落的收尾速度无影响。为验证这一假设,笔者尝试使用相同的锤头及泥浆参数,改变土体参数进行5组模拟,结果表明5组工况下的锤头时间-速度曲线基本重合,速度方差为6.4×10-7,证明假设成立,故在后续模型中不再考虑土体类型的影响。
2.1.4 工况表
影响锤头收尾速度的主要因素为锤头质量及泥浆阻力,在进行有限元模拟时,前者可由锤头的大小即锤头直径作为控制指标,后者可由泥浆密度、黏度和锤头泄浆孔半径作为控制指标。针对4个控制指标各设置7组工况来研究其对锤头收尾速度的影响,工况情况见表3。
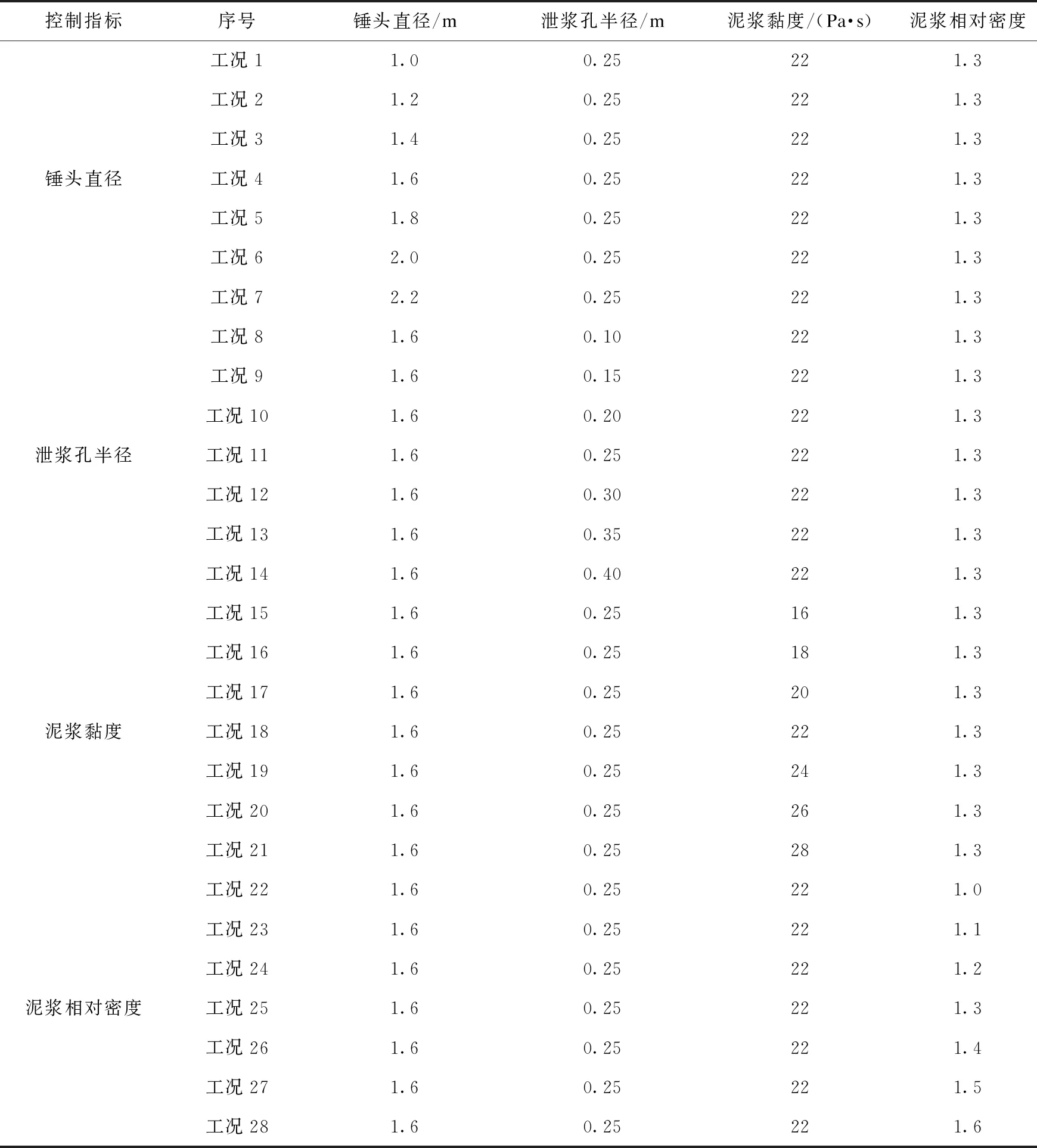
表3 工况表
考虑到工程实际,所有模拟工况对应的泥浆孔半径均比锤头半径大1 cm。对于工况1~工况7中的锤头直径变化,均是以工况4中1.6 m锤头(对应高度1.8 m)为基础等比例缩小、放大得到。
2.2 模拟结果与分析
图1为锤头排开泥浆下落时的有限元模拟示意图。工况1~工况7的锤头下落时间-速度曲线见图2,可以看出,锤头质量对收尾速度有明显影响,锤头直径为1 m(对应质量1 834.44 kg)时,锤头的收尾速度为1.2 m/s;当锤头直径为2.2 m(对应质量19 516.19 kg)时,锤头的收尾速度达到2.1 m/s,可见锤头质量与收尾速度明显正相关,锤头质量越大则下落速度越快,冲击功也越大。但实际工程中,由于受钻孔直径的限制,锤头直径不能自由加大或减小,且锤头材质较为统一,密度难以改变,故通过增大锤头质量的方式增加锤头速度比较困难。
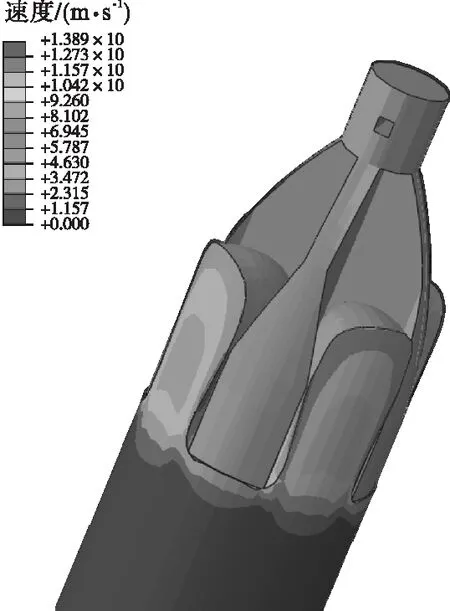
图1 锤头下落示意图
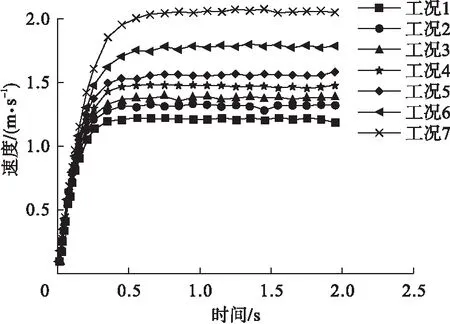
图2 锤头直径变化的时间-速度曲线
工况8~工况14的锤头下落时间-速度曲线见图3,可以看出,泄浆孔半径越大对收尾速度越有利。泄浆孔半径变大,则锤头底面接触泥浆的面积变小,在下落过程中受到的泥浆碰撞阻力变小,速度会增大[16]。但是增大泄浆孔半径意味着减小锤头质量,这与工况1~工况7锤头质量与收尾速度成正比的结论冲突,可见增大泄浆孔半径比一味增加锤头质量更具有经济效益;但是增大泄浆孔半径也意味着会减小锤头的底面积,不利于破岩挤土,实际工程中需要谨慎衡量。
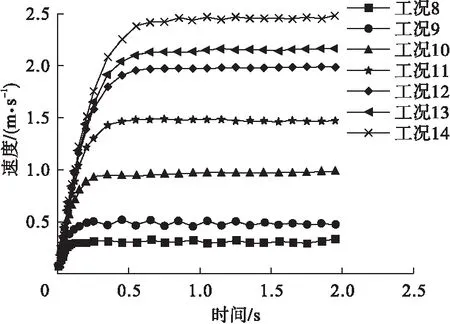
图3 泄浆孔半径变化的时间-速度曲线
工况15~工况21的锤头下落时间-速度曲线见图4,可以看出,泥浆黏度变化对锤头下落速度影响很小。

图4 泥浆黏度变化的时间-速度曲线
黏度表现为液体运动时各分子或颗粒间产生的内摩擦力,是反映液体流动行为的特征。对钻孔灌注桩而言,黏度越大的泥浆在孔壁上产生的泥皮越厚,对阻隔渗漏、维护孔壁稳定有利。但黏度过大,钻进过程中易“糊钻”,造成泥浆泵故障,增加泥浆净化的困难,从而影响钻进速度。
工况22~工况28的锤头下落时间-速度曲线见图5,可以看出,泥浆相对密度越大锤头收尾速度越小。泥浆相对密度大时,泥浆对孔壁的侧压力大于孔隙水压力,对维护孔壁稳定有利,同时泥浆相对密度越大携带钻渣的能力也越大。但比重过大,失水量亦会增大,孔璧上的泥皮也增厚,增加了泥浆原料的消耗,而且会给清孔和灌注混凝土造成困难。泥浆相对密度增大,意味着泥浆中固体颗粒含量增大,还会对钻具产生较大的磨损。
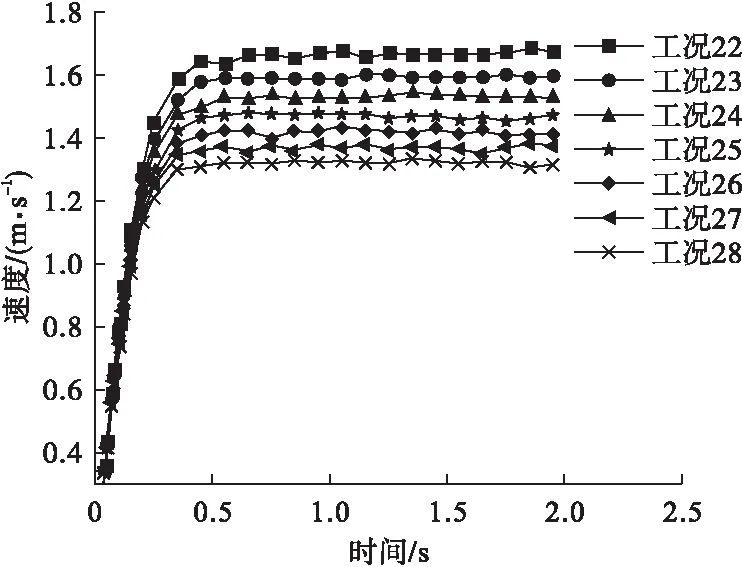
图5 泥浆相对密度变化的时间-速度曲线
3 最佳提钻高度的拟合函数
模拟发现,锤头在下落过程中很快就能达到收尾速度,各工况的平均收尾时间为0.5 s,且0.5 s对应的锤头位移均不超过1 m,说明锤头在下落不超过1 m的距离就达到收尾速度,之后速度将保持不变,即锤头用于破岩挤土的触底动能将保持不变。传统工程经验认为在砂卵石层等坚硬密实的岩层中,应当通过提高钻机冲程的方式增加掘进速度[20],这显然是不对的,提高钻头高度并不能有效增加锤头的冲击功。
3.1 锤头质量与对应收尾高度关系分析
在对工况1~工况7的锤头质量与收尾高度的关系分析时发现,虽然锤头直径越大收尾速度越快,但锤头直径与收尾高度没有明确的相关性,究其原因在于改变锤头直径时,锤头体积及表面积也一并改变,这将影响泥浆的黏滞阻力及碰撞阻力作用,未达到控制单一变量的初衷,故笔者又通过改变密度、保持锤头大小不变的方式来增加锤头质量,密度及质量参数见表4,泄浆孔半径取0.25 m,泥浆黏度取22 Pa·s,泥浆比重取1.3,最终得到了图6中的散点图。此处改变密度是为了接近前文工况1~工况7中的锤头质量,目的仅仅是得到锤头质量与收尾速度的理论对应关系。
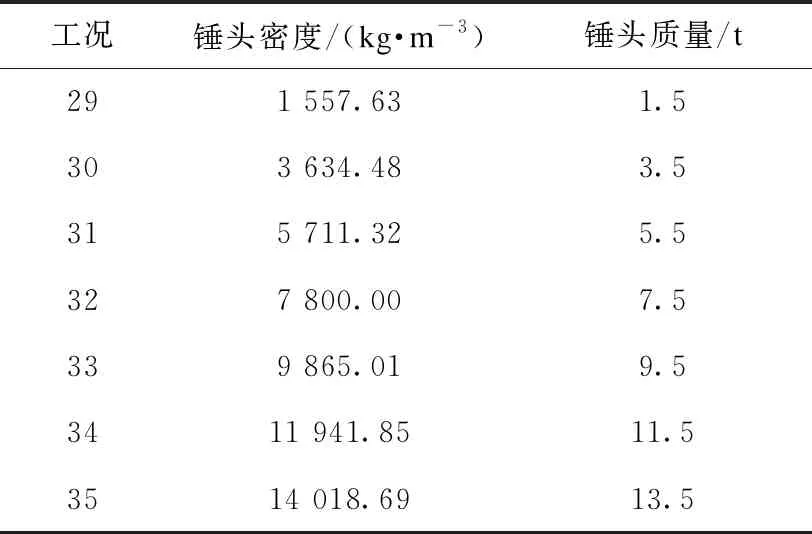
表4 锤头密度变化工况表
锤头质量与对应收尾高度的散点图如图6所示,从图中可以看出,锤头质量与收尾高度大致呈线性关系,对其进行线性拟合,拟合曲线过原点,原因在于锤头质量为0时不会下落,对应收尾高度为0,由此可设拟合函数为
Hm=KmXm.
(6)
式中:Hm为锤头质量对应的收尾高度;Km为锤头质量对应的拟合系数;Xm为锤头质量。
计算后求得Km=0.037 2,得到一次多项式拟合函数:
Hm=0.037 2Xm.
(7)
绘制图6中的理论曲线图,二者方差为0.018 4,方差越接近0拟合结果越好,文中方差达到10-2级,说明拟合度良好。
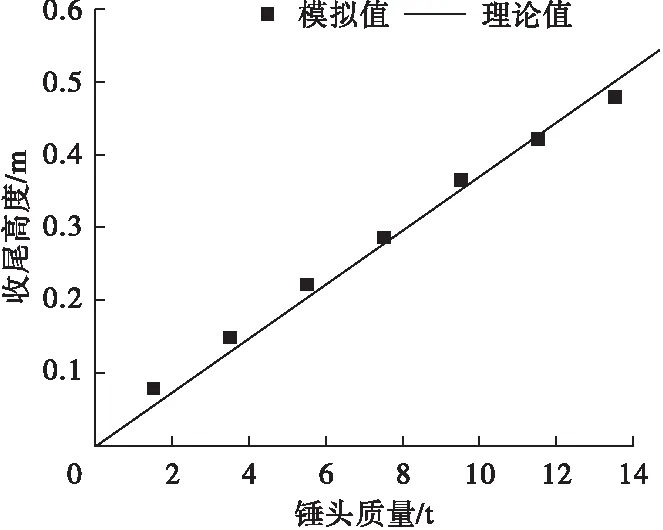
图6 锤头质量与对应收尾高度关系图
3.2 泄浆孔半径与对应收尾高度关系分析
泄浆孔半径与对应收尾高度的散点图如图7所示,从图中可以看出,锤头质量与收尾高度近似呈指数关系,但考虑到其余变量均使用的多项式函数拟合,此处若使用指数函数拟合,将不利于后文最佳提钻高度的公式推导。
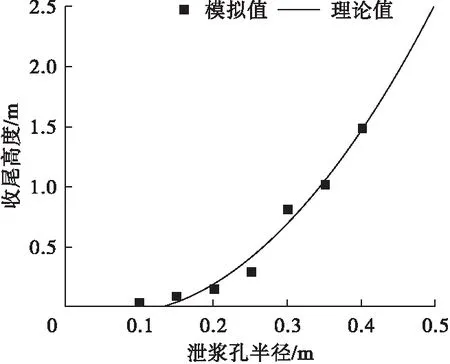
图7 泄浆孔半径与对应收尾高度关系图
因此使用多项式函数拟合,拟合曲线应当过原点,原因在于锤头泄浆孔半径为0时,根据泥浆的不可压缩特性可知锤头不会下落,收尾高度为0。
在使用一次多项式函数拟合后得到模拟值与理论值的方差为0.327 7,绘图后发现拟合曲线与模拟值偏离严重,因此尝试使用二次多项式拟合,设函数为
(8)
式中:Kd1及Kd2为二次多项式拟合的系数。
求得Kd1=-1.840 9,Kd2=13.811 1,得到二次多项式拟合函数:
(9)
绘制图7中的理论曲线图,二者方差为0.085 5,拟合度良好。
笔者又继续进行三次、四次多项式拟合,方差分别为0.091 8和0.092 0,发现次数越大拟合结果反而不好,因此最终选用了二次多项式的拟合结果。
3.3 泥浆黏度与对应收尾高度关系分析
泥浆黏度与对应收尾高度的散点图如图8所示,从图中可以看出,模拟值近乎在一条直线上,模拟值之间的方差为2.19×10-7,说明泥浆黏度变化的影响很小。
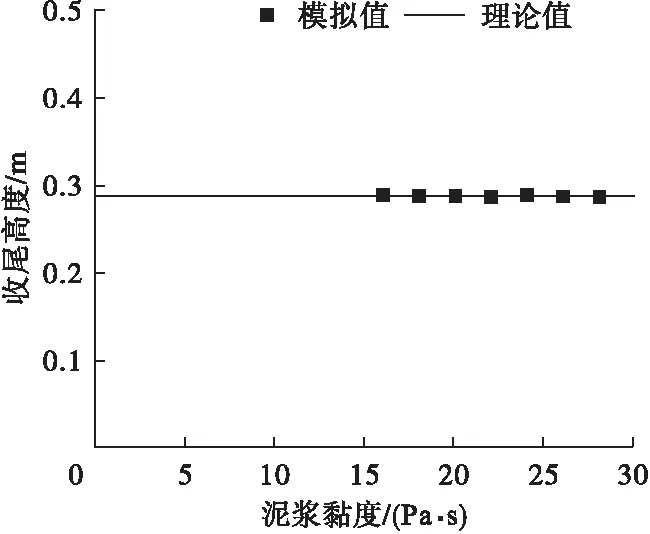
图8 泥浆黏度与对应收尾高度关系图
因此设函数为
Hv=Kv.
(10)
式中:Hv为泥浆黏度对应的收尾高度;Kv为泥浆黏度对应的拟合系数。
计算后求得Kv=0.287 4,得到拟合函数:
Hv=0.287 4.
(11)
绘制图8中的理论曲线图,二者方差为4.679 6×10-4,近似于0,拟合度很好。
3.4 泥浆相对密度与对应收尾高度关系分析
泥浆相对密度与对应收尾高度的散点图如图9所示,从图中可以看出,泥浆相对密度与收尾高度呈反比关系。
首先假设一次拟合函数为
Hw=Kw1+Kw2Xw.
(12)
式中:Hw为泥浆相对密度对应的收尾高度;Kw1及Kw2为一次多项式拟合的系数;Xw为泥浆相对密度。
求得Kw1=0.608 1,Kw2=-0.236 3,得到一次多项式拟合函数:
Hw=0.608 1-0.236 3Xw.
(13)
绘制图9中的理论曲线图,二者方差为0.012 9,拟合度良好。
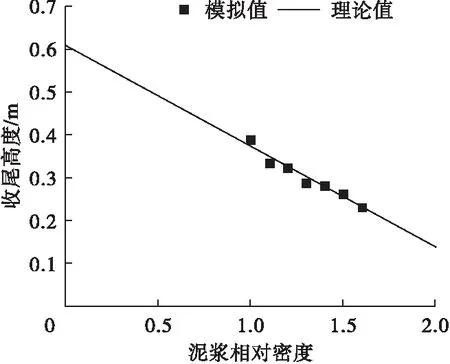
图9 泥浆相对密度与对应收尾高度关系图
笔者又继续使用二次多项式拟合,得到对应的方差为0.012 2,与一次拟合函数相比,方差的缩减幅度非常小,因此使用一次拟合函数就已经足够了,没有必要为了追求更小的方差而使用高次多项式。
3.5 锤头收尾高度的函数表达式
在分别得到4类指标对应的拟合函数后,为了更加直观的得到一个有关最佳提钻高度的统一表达式,使用最小二乘法将4个独立函数整合在一起,设函数表达式为
(14)
式中:K1为泥浆黏度及泥浆相对密度对应的常数项;K2~K5为与3个相关变量对应的系数。
求得K1=0.446 7,K2=0.033 7,K3=-5.667 7,K4=21.232 9,K5=-0.236 3,最终方差为0.046 7,拟合结果良好。由此得到最佳提钻高度的函数表达式为
H=0.446 7+0.033 7Xm-5.667 7Xd+
(15)
将式(15)用于工况8~工况35计算理论值,与模拟值一起绘于图10,二者吻合良好。
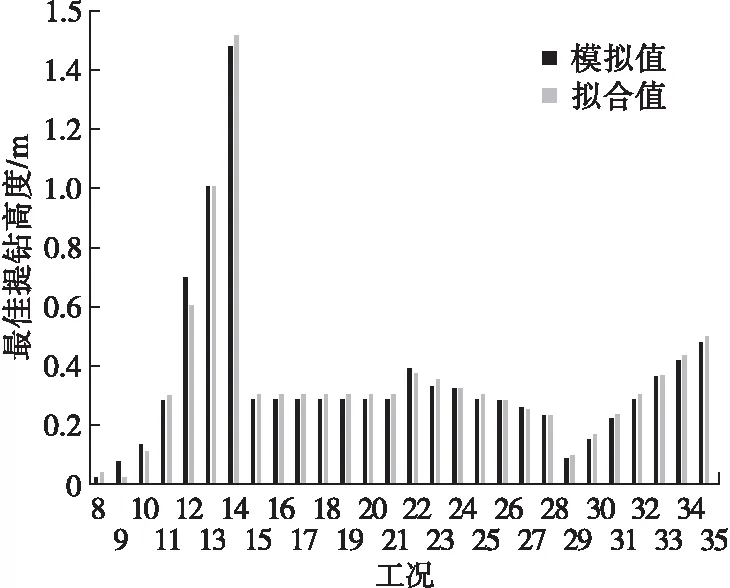
图10 最佳提钻高度的模拟值与拟合值
4 结 论
(1)由锤头在泥浆中的下落时间—速度曲线可得,锤头在下落约0.5 s后达到最大速度,达到最大速度后的瞬间触底可最快完成单次冲击,实现成孔效率最大化。
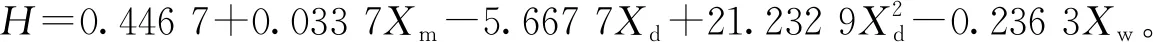
(3)笔者发现在工程中经常采用增加提钻高度来增加锤头冲击功的方式是有误的。锤头达到收尾速度所需高度一般不超过1 m,当提钻高度超过收尾高度后,锤头的冲击功将不再增加,锤头多余的势能不是转化为锤头动能,而是被泥浆阻力耗散转化为泥浆热能及泥浆动能。
