地下厂房锚杆支护的反向传播神经网络智能化设计模型

姚添智, 张建海*，刘桂泽，程东昱，李治国，李永红

(1.四川大学水力学及山区河流开发与保护国家重点实验室，成都 610065；2.中国电建集团成都勘测设计研究院有限公司，成都 610072)

水电站地下厂房是一个庞大的、复杂的地下建筑结构，其地下洞室稳定性受到诸如地质构造、洞室跨度、地应力大小以及支护强度等因素影响[1]。近年来，在中国西部高山峡谷的高地应力区建成的水电站地下厂房例如锦屏一级、白鹤滩、猴子岩等出现了诸如片帮剥落、劈裂破坏、弯折内鼓等围岩变形破坏现象，这就对洞室支护设计提出了更高的要求。对于地下厂房，目前普遍采用系统锚杆和锚索支护法对洞室围岩进行加固，这一方法可以很好地发挥围岩的强度和自身承载力[2]。中国很多学者对锚杆支护进行了大量的研究，胡田清等[3]基于百余个水电站地下厂房资料，开发了“地下厂房数据库系统”，该系统具有围岩稳定分析的功能并可通过配合经验支护参数对地下厂房主厂房支护方案进行设计；周述达等[4]通过对中国17座已建的大型电站地下厂房跨度、高度与支护参数进行回归分析，建立了厂房不同部位锚杆支护方案与洞室规模的关系，据此对水电站地下厂房进行系统支护设计。但是地下厂房的支护设计在方法上仍然以工程类比法为主[5]，而且对高地应力区的大型地下厂房围岩变形特征认知不足，缺乏相关设计经验，不足以全面指导洞室的支护设计。

人工神经网络理论是一种解决非线性问题的科学，葛宏伟[6]等介绍了神经网络在岩石力学参数识别与应力分析、参数预测、岩体稳定性研究、岩体变形预测、岩石工程反分析等多种方向的应用，为岩石力学领域的研究提供了新的思路。目前应用最广泛、最成熟的神经网络模型为反向传播神经网络(back propagation，BP)。BP神经网络是一种多层前馈神经网络，广泛应用于非线性建模、函数逼近、逻辑分类等方面。基于BP神经网络理论，通过研究中外26个跨度在18.0～34.0 m，强度应力比在2.00～80.8之间的水电站地下厂房的锚杆支护方案，以Octave语言作为编写工具，建立水电站地下厂房系统锚杆支护的智能化设计模型(简称“智能化设计模型”)。该模型能实现通过输入洞室跨度以及强度应力比来获得地下厂房锚杆支护方案的功能，并且根据神经元之间的权重关系分析洞室跨度和强度应力比对系统锚杆支护方案的不同影响程度。

1 BP神经网络模型设计与实现

1.1 模型建立

1.1.1 输入层的设计

肖丛苗等[7]针对大跨度地下工程安全风险高的问题，采用理论分析、经验评价、数值模拟的综合评价方法，优化分析得出适用于硬岩条件下大跨度结构的理论分析法，并采用Q评价系统和工程类比法确定了大跨度地下工程锚杆、锚索和喷射混凝土的支护参数。苏国韶[8]以高地应力地区黄河拉西瓦水电站地下厂房大型洞室群为研究背景，综合应用智能优化技术、机器学习以及数值模拟方法，提出了高地应力下大型地下洞室群稳定性分析与智能化优化的新方法，解决了高地应力下大型地下洞室群开挖与支护方案的大规模全局优化问题。根据上述研究现在确定地下厂房系统锚杆支护的智能化设计模型输入参数为洞室跨度B和强度应力比Kσ，强度应力比的计算公式为

(1)

式(1)中：Kσ为强度应力比；Rc为单轴抗压强度；σ1为最大主应力。

1.1.2 输出层的设计

通过分析已建成的水电站地下厂房锚杆支护的方案，将锚杆支护方案分成了6种，编组方案如表1所示，其中，d为锚杆直径，a为锚杆间距，b为锚杆排距。

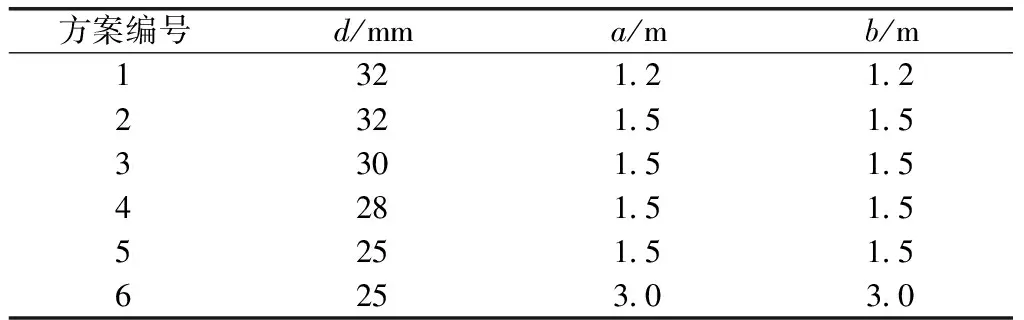
表1 锚杆支护方案

1.1.3 隐含层设计

隐含层的层数和节点数目都影响着预测结果，理论上隐藏层层数越多，预测结果的误差越小，但是隐藏层数目过多又会导致网络结构过于复杂，计算速度慢，参照典型的BP神经网络结构选择隐藏层层数为1层。

隐藏层节点数的选择与输入输出单元数有着直接的关系，但是至今仍没有一个很好的解析公式，隐藏层节点过多会导致学习时间过长；而隐藏层节点数过少则容错性很差，根据前人经验，计算节点数[9]，即

(2)

式(2)中:m为隐含层节点数；n为输入层节点数；l为输出层节点数；α为1～10之间的常数，α取值为7，根据式(2)选取隐藏层节点数为10层。

1.1.4 建立合适的神经网络结构

建立一个适用于水电站地下厂房系统锚杆支护设计的神经网络结构，用于研究水电站地下厂房的洞室跨度和强度应力比与不同系统锚杆支护方案之间的关系。由图1可知，该神经网络结构输入层含有2个单元，分别输入洞室跨度和强度应力比，隐藏层含有10个单元，输出层含有6个单元分别对应表1的6种不同的支护方案。

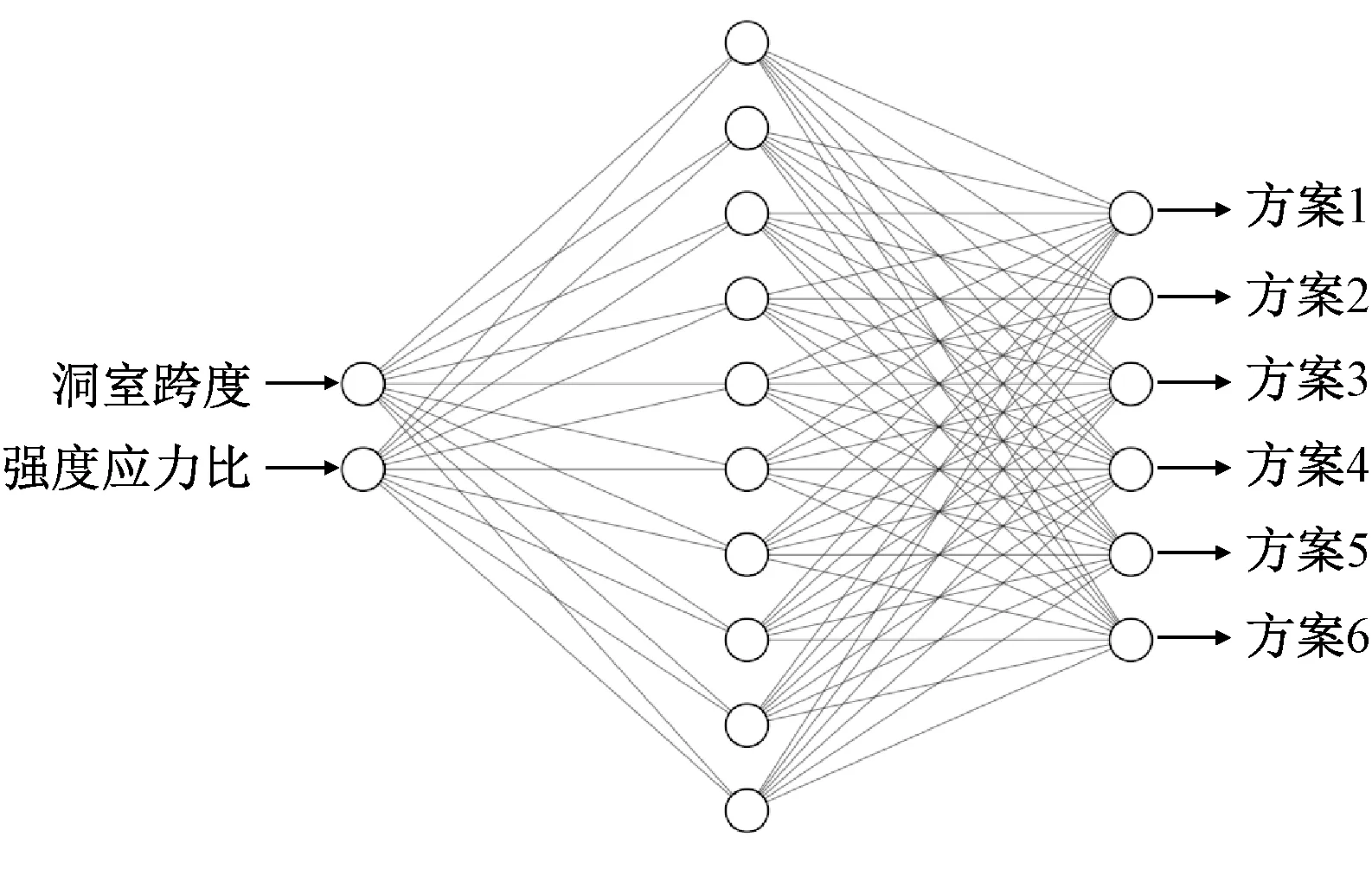
图1 BP神经网络结构图

1.2 模型训练

基于BP神经网络的智能化设计模型的训练过程如图2所示。

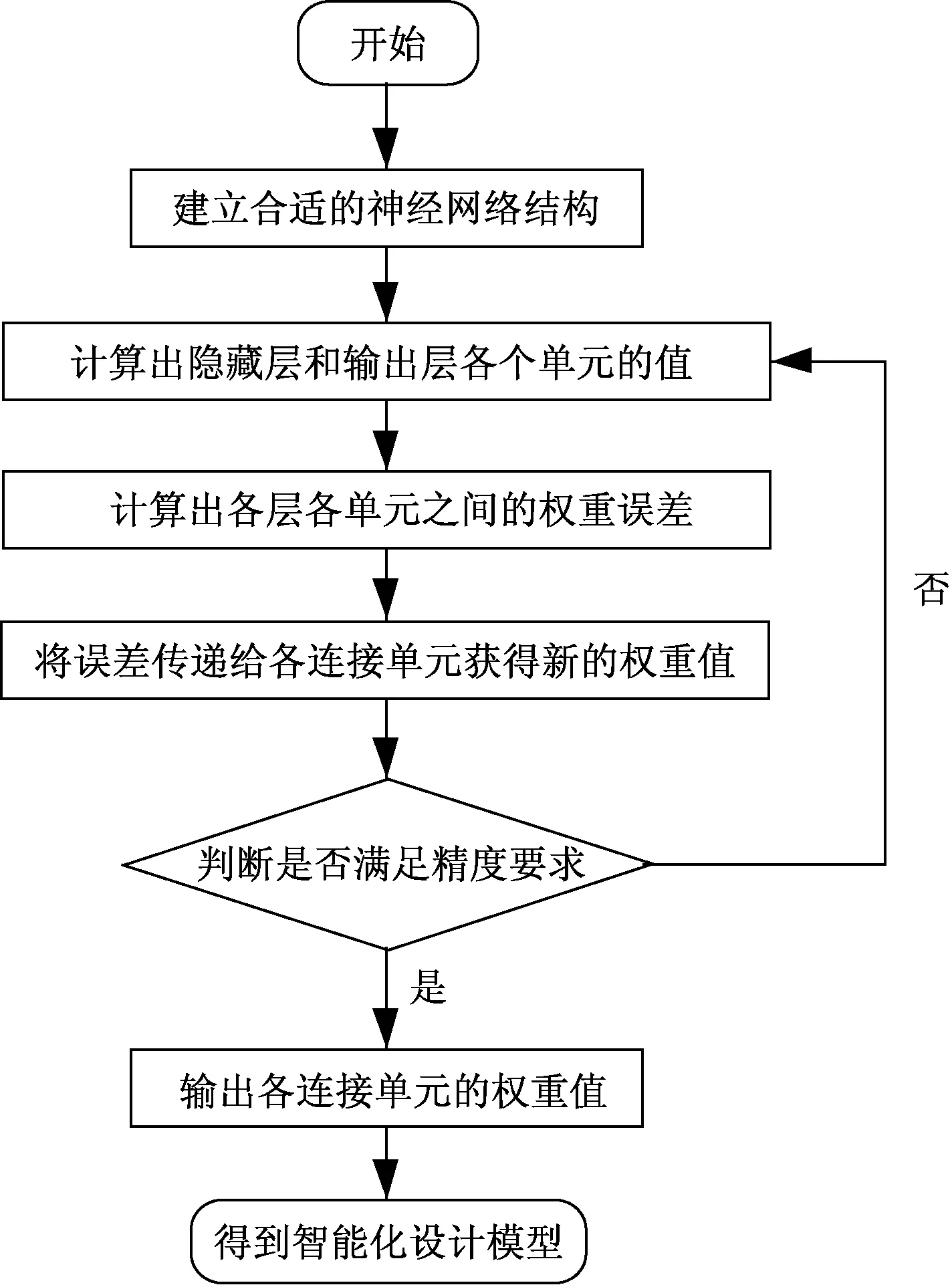
图2 模型训练流程

第一步建立适用于智能化模型的神经网络结构，如图1所示。

第二步初始化神经网络的权重值。

第三步输入训练集数据对神经网络进行前向传播获得初次训练的模型，得到神经网络中各单元的值。

第四步计算初次训练模型的输出层误差值并将其传递给隐藏层，以此来更新输出层和隐藏层之间的权重。同理计算隐藏层到输入层之间的误差，并更新其权重值。

第五步在获得全新的权重值以后得到新的模型，通过验证集对模型进行验证，如果不满足验证集的要求则重复第四步，如果满足则得到最终的智能化支护模型。

1.3 模型训练逻辑

1.3.1 前向传播

首先通过前向传播对网络进行训练。设样本集为X，神经网络的第二层(隐藏层)为a2，第三层(输出层)为a3，Θ(i)为第i层到第i+1层的权重值，初始的Θ(i)是随机设置的，样本期望输出为y，h为实际输出，前向传播公式为

a2=sigmoid[Θ(1)×XT]

(3)

a3=sigmoid[Θ(2)×XT]

(4)

h=a3

(5)

(6)

式中：sigmoid为传递函数。

1.3.2 代价函数

因为初始Θ(i)是随机设置的，所以此时得到的实际输出值h与期望输出值y有很大的误差。为了评价实际输出值h的准确程度，引入代价函数J(Θ)的概念，表达式为

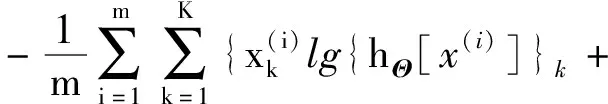
(7)

当值J(Θ)越小的时候代表着实际输出值h与期望输出值y越接近，代表权重Θ的取值越好，所以当J(Θ)值最小的时候即是Θ的最优解。

1.3.3 反向传播

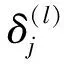
(8)

δ(2)=[Θ(2)]Tδ(3)×g′[z(2)]

(9)

g′[z(2)]=a(2)[1-a(2)]

(10)

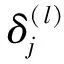
Δ(l)=Δ(l)+δ(l+1)[a(l)]T

(11)

使用式(11)中获得的Δ(l)更新权重θ，然后通过Octave中的最小化连续微分多元函数fmincg来获取最优的权值。

2 模型设计与实现

2.1 模型实现

2.1.1 训练样本及验证集

选取23个水电站地下厂房边墙系统锚杆支护参数为训练样本，分别选取3个不同强度应力比的地下厂房为验证集和测试集[10-16]，训练集数据如表2所示，验证集数据如表3所示，测试集数据如表4所示。

表2 训练样本集

表3 验证集数据

表4 测试集数据

2.1.2 模型实现

使用Ocatve中的fmincg函数求得代价函数值J(Θ)的最优解，即可得到从神经网络输入层到输出层的最优权重值。由图2可知，当权重值θ确定后即可通过输入地下厂房洞室跨度B和强度应力比Kσ来输出锚杆支护方案，此时式(3)、式(4)中的X由样本的训练集变成了测试对象的输入参数。锚杆支护设计模型通过Octave窗口实现交互，模型运行窗口如图3所示。

图3 模型运行窗口

以黄金坪水电站地下厂房为例，通过输入洞室开挖跨度B以及强度应力比Kσ，模型会自动输出锚杆支护方案，结果如图4所示。

图4 模型测试示意图

2.2 模型验证及讨论

将表4收集的测试集数据输入到智能化设计模型中，可得到该模型建议的系统锚杆设计方案，如表5所示，通过模型预测方案与实际工程使用方案的对比来验证智能化设计模型的可靠性。

由表5可知，白山水电站的系统锚杆设计模型的建议方案与实际工程使用的方案一致，二滩水电站建议方案锚杆直径Φ30 mm，锚杆间排距@1.5 m×1.5 m黄金坪水电站建议使用方案为锚杆直径Φ32 mm杆间排距@1.2 m×1.2 m比于实际工程使用的方案更加的安全可靠。

表5 智能化设计模型建议的支护方案表

借助文献[10]提出的支护指数Ib的概念和相应的计算公式对所有已收集工程的智能化设计模型建议方案与实际工程的支护设计方案进行了对比评价，当支护指数Ib=0.8～1.2时支护强度相对合理，Ib>1.2时支护强度偏高，Ib<0.8时支护强度偏低。

支护指数Ib表达式为

(12)

ΔCb为围岩凝聚力增量，计算公式为

(13)

[ΔCb]为开挖跨度B和强度应力比Kσ与围岩凝聚力增量ΔCb的拟合得到的经验公式，即

(14)

式中：η为群锚效应系数；τs为锚杆的抗剪强度；S为锚杆截面积，取η=3.5，τs=300 MPa。

将表2～表4的工程代入智能化设计模型中，并根据式(12)～式(14)计算出智能化设计模型建议方案的支护指数，与实际工程使用的方案进行对比分析，结果如图5所示。

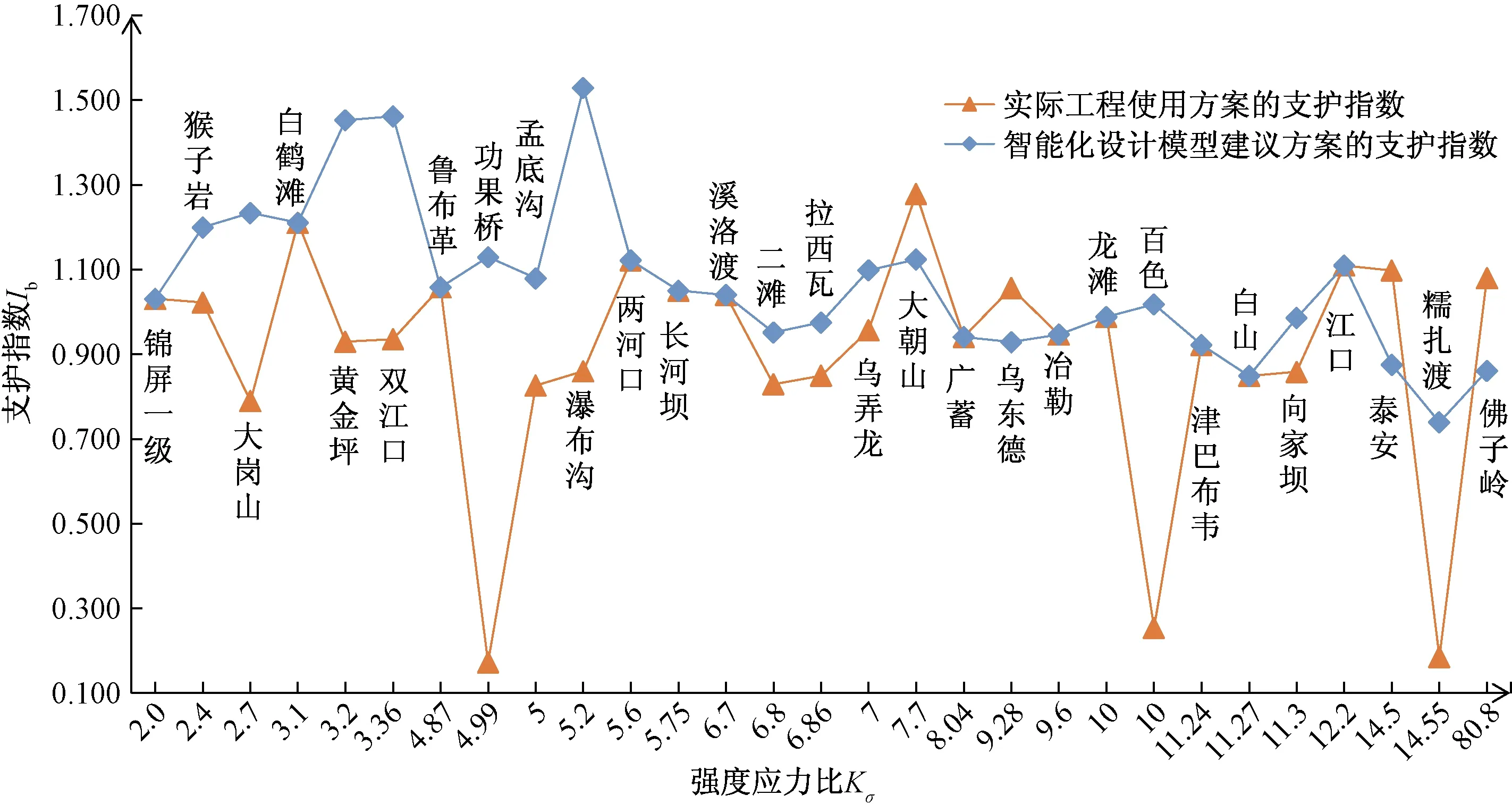
图5 智能化设计模型建议方案与实际工程方案的支护指数对比图

在高地应力地区，工程类比法的工程经验项目较少，难以为不同开挖跨度与强度应力比的工程提供可靠的支护方案参考。所以在实际工程中可能会出现如图5中大岗山水电站的设计支护强度偏低的问题，给施工期造成安全隐患。在中低应力地区，通过传统方法设计的孟底沟、百色和糯扎渡水电站同样出现了系统锚杆支护强度偏低的状况，说明工程类比法在遇到高地应力和不常见的洞室开挖跨度等情况下难以选择适当的系统锚杆支护方案，设计可靠度较低。但是智能化设计模型所建议方案的支护强度普遍优于实际工程使用的方案，且支护指数均在1附近，没有简单地通过提高支护指数而造成经济上的浪费。在相对复杂的高地应力地区，如猴子岩、大岗山水电站，智能化设计模型都提供了比实际工程更安全的设计方案。由此可见，智能化设计模型相较于传统的工程类比法，提供的支护方案可靠性更高且可以保证工程项目的经济性，可以为实际工程中的地下厂房系统锚杆设计提供参考。

3 支护方案影响因素的讨论

3.1 神经网络评价权重的计算方法

不同的系统锚杆支护方案代表着不同的支护强度，在地下厂房洞室中系统锚杆支护方案的选择受到多种因素影响，但是目前还未明确哪一项指标为主要的影响因素。针对本文提出的智能化设计模型，可以通过对各神经元之间的权重的分析处理，进一步探究开挖跨度和强度应力比对系统锚杆支护方案选择的不同影响程度。

为此可以借助以下几项指标来描述其关系。

(1)相关显著性系数rij，其表达式为

(15)

式(15)中:i为神经网络输入单元，i=1,2，…,m；j为神经网络输出单元，j=1,2，…,n；k为神经网络的隐藏单元，k=1,2，…,p；ωki为输入层神经元i和隐藏层神经元k之间的权系数；ωjk为输出层神经元j和隐藏层神经元k之间的权系数。

(2)相关指数Rij，其表达式为

(16)

(3)绝对影响系数Sij，其表达式为

(17)

绝对影响系数Sij可以用来评价不同输入单元对于输出结果的影响程度，某个输入单元的Sij越大说明对于结果的影响越大[17]。

3.2 评价因素权重的确定

根据训练得到的各个神经元之间的权系数如表6所示。

表6 智能化设计模型的神经网络权值

根据BP神经网络得到的权重值可以通过式(16)～式(18)分析两种输入参数对锚杆支护方案选择的影响权重。表7计算了开挖跨度和强度应力比对6种系统锚杆支护方案的影响权重。

由表7可知，在智能化支护设计模型中强度应力比对于结果影响的权重值均大于开挖跨度的权重值，所以在仅考虑洞室跨度和强度应力比的时候，强度应力比的变化对于地下厂房系统锚杆支护方案的不同选择具有更大的影响。

表7 开挖跨度和强度应力比对支护方案的权值计算

4 结论

(1)基于BP神经网络理论，提出地下厂房系统锚杆支护的智能化设计模型。使用Octave作为开发语言，实现了通过输入水电站地下厂房开挖跨度和强度应力比获得了系统锚杆支护方案的功能。

(2)系统锚杆支护设计模型收集了中外29个水电站地下厂房地质条件、厂房规模、系统锚杆支护参数等资料。所收集地下厂房的洞室跨度为18.0～34.0 m、强度应力比为2.00～80.8，使该模型具有较高的可信度和代表性。

(3)选取了黄金坪、二滩、白山水电站作为高、中、低3种不同地应力条件的工程案例用于验证设计模型的可行性。相比于实际工程，智能化设计模型为黄金坪和二滩水电站提供了更加安全、可靠的支护方案。

(4)借助支护指数的概念，对比了智能化设计模型建议的支护方案与实际工程使用的方案的支护强度。结果表明智能化设计模型建议的支护方案更加的稳定、安全，并且在高地应力条件下仍然可以达到理想的设计效果。为以后全面建立地下厂房支护方案设计模型奠定了基础。

(5)通过计算绝对影响系数，得到强度应力比和开挖跨度对于不同支护方案选择的权重。根据计算结果可知，在只考虑开挖跨度和强度应力比的情况下，强度应力比对于系统锚杆支护方案的选择影响更大。此方法为研究不同因素对系统锚杆支护方案选择的影响提供了新的思路。