基于高维张量分解的个性化教育资源推荐算法研究

何英 许文

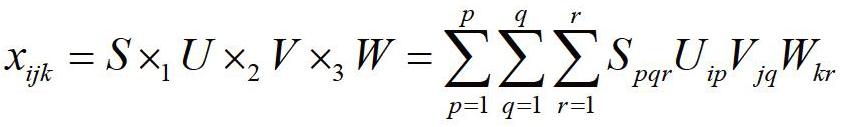
摘 要：随着互联网及在线教育平台的加速发展，积累了大量的教育资源，学习者对网络平台中教育资源的利用依赖性不断提高，但需要花费大量的时间和精力去筛选符合自己的资源[1]。目前，在线平台为学习者们提供的内容基本相同，未能针对个性化的要求提供差异化的资源[2]。文章所构建的基于高维张量分解的个性化教育资源推荐算法，在分解中能够保留高维空间的信息完整性，避免了传统推荐算法在分解中原始信息和特征的丢失，从而为个性化学习资源推荐的研究提供参考。

关键词：高维张量分解;个性化;教育资源;推荐算法

0 引言

目前，个性化推荐技术已经在互联网及电子商务（淘宝、京东等平台）中使用，效果也尤为显著[3]，近几年个性化推荐技术已经逐渐成为教育资源领域应用的研究热点，从而使学习者与教育资源之间形成“找”和“推”的双向模式。学习者对教育资源的选择会根据学习目标、学习风格等不同因素产生不同个性化需求，这使得教育资源推荐变得非常复杂。推荐系统起源于信息检索相关技术，推荐系统的性能和结果质量优劣与推荐方式和推荐策略有着极大的关联，而推荐系统的核心是推荐算法[1]。

我国推荐算法研究时间较短，2005年，张晗等通过Apriori算法建立关联规则，将所得频繁项用个性化教育资源方式呈现出来。后期他们再次建立全新智能教育资源推荐系统，将信息查找与挖掘、联机分析处理等技术结合完成有效推荐[3]。2017年由Andrew G，GaoJ等人提出了一种新的基于矩阵的推荐方法，可向用户提供更有效的学习服务，促使用户制定切实可行的学习计划。由于互联网的信息越来越多，维度越来越高，生活中常见的空间位置信息、视频流数据、图像信息、文档集资料等都是高维数据，使用传统的方法将高维的数据转换成矩阵形式，会破坏原有数据的张量结构，造成数据和信息的损失，影响最终的分析结果准确性。因此，如何获取学习者的个性信息，很好地保留学习者教育资源选择的数据信息结构，设计基于高维张量分解的个性化教育资源推荐算法，对于提高推荐的教育资源精度、提升学习者的学习效率具有十分重要的价值[1]。

1 高维张量分解的个性化教育资源推荐方法

1.1  学习者特征模块

文本在自然情境下采用访谈法开展[4]，选择的访谈对象为高职教育技术研究者和某高职2019级学习“软件测试基础”课程的学生。选取的访谈对象中两位教师均具有多年的教学经验，专业或研究方向为教育技术学，能够保证访谈的结果具有科学性和代表性。

针对文本所指的教师和学生进行访谈后确定个性化推荐系统中推荐的内容与影响因素。一是推荐内容，感兴趣的知识点。二是影响因素，在资源推荐过程中主要影响因素包括学习者属性信息、特征信息、行为轨迹信息等数据。

1.2  教育资源模块

如何准确地对教育资源进行建模是实现个性化教育资源推荐的关键。本文根据国内外典型的教育资源模型规范要求定义了以下几个方面的内容：知识摘要信息、教育资源类型、资源难度系数、估计学习时间以等[1]。模型中的基本信息包括资源的名称、容量大小、作者、上传的时间和存放路径等内容。

1.3  学习情景模块

学习者可以从信息化教学平台获取文字图片、音频、视频等多种教育资源，同时学习者也可以从不同形式的教育资源构建丰富多彩的学习环境，从而形成一种不受时空限制且包含丰富音频、视频资源的学习方式，可以调动学生的学习兴趣。

1.4  高维张量在个性化教育资源推荐上的算法研究

目前推荐系统在多维信息联合应用方面仍存在不足，还有较大的提升空间，推荐系统是在矩阵分解模型的基础上发展起来的，从而衍生出了张量分解模型，张量分解可以提取3种影响因素之间的潜在关系信息[5]。目前大多数基于张量分解的推荐算法采用CP分解或Tucker分解进行优化[6]，通过Tucker分解可以获取高维数据的特征信息，CP分解是Tucker分解的一种特殊形式，如果张量模型中的各维度的数目相等且核心张量是对角的，那么Tucker分解就退化成了cp分解，本文所采用的资源推荐参考因素转化成三维数据时，各维度的数目并不相等。因此，更适合使用Tucker分解。

1.4.1  张量分解

高维张量是由三阶张量推广得到的高维空间，由一个三阶的张量分解可得高维的张量分解，一个三阶张量的定义为：，其中I，J，K是张量的维度，x∈RI*J*K，同理高阶张量的表达式为：

1.4.2  Tucker分解

在张量分解模型中应用比较广泛的推荐算法是Tucker分解[7]，将三阶张量分解成一个核心张量与3个因子矩阵的乘积如公式为：，其中U∈RM×r1，V∈RN×r2，W∈RK×r3是正交矩阵，张量G∈Rr1×r2×r3被称为Tucker分解的核心张量，元组（r1×r2×r3）可以被称为多线性的秩。同理高阶张量的索引模式可表示为：

1.4.3  学习者教育资源推荐算法

张量分解方法就是在三维张量上引用Tucker分解方法，这样能够降低张量的维度[8]。本文抽取学习者、教育资源、学习情景三个维度的特征，输入“学习者-教育资源-学习情景”{s，e，c}三元组的数据构建初始张量x，，其中IS，IE，IC分别代表数据中学习者，教育资源，学习情景的元素。

根据初始张量x进行Tucker分解，将构建的三维张量分解为学习者特征矩阵U、教育资源V、学习情景W以及核心张量S，那么张量分解的公式如下所示：

根据教育资源特征矩阵里面的每行的特征之和，可得特征之和越大，就说明教育资源推荐的越能受到学习者的喜好，反之值越小，就说明推荐的教育资源不受到学习者的喜好。

2 结语

学习者教育资源的推荐系统就要考虑到个性化所涉及的多样性等问题，此时，个性化推荐显得非常重要。教育资源作为教育行业服务领域的研究方向之一，它在信息化教学平台资源库的建设中是必不可少的。本文从学习者个性化教育资源角度出发，将张量Tucker分解成功融合应用到资源推荐上，设计了一种基于高维张量分解的个性化教育资源推荐算法。将现有经典张量分解算法和理论推广到高维张量，研究“学习者-教育资源”高维张量的分解算法，并对算法的效率进行研究，为个性化精准教育资源推荐提供技术基础。

[参考文献]

[1]李光泉.基于学习者个性的教育资源推荐服务研究[D].南昌：江西财经大学，2018.

[2]卫文婕，付宇博.个性化学习资源推荐算法研究[J].中国教育信息化，2018（18）：91-96.

[3]刘静，熊才平，丁继红，等.教育信息资源个性化推荐服务模式研究[J].中国远程教育，2016（2）：5-9，79.

[4]马秀麟，梁静，李小文，等.智能化学习环境下资源推荐的影响因素及权重的探索[J].中国电化教育，2019（3）：110-119.

[5]楊晓蕾，李胜，何熊熊，等.基于张量分解的多维信息融合兴趣点推荐算法[J].小型微型计算机系统，2020（5）：902-907.

[6]汪亮.稀疏高阶张量CP分解[D].广州：广东工业大学，2019.

[7]刘振娇，王新华.基于上下文学习和张量分解的个性化推荐[J].山东师范大学学报（自然科学版），2017（1）：36-42.

[8]胡强.基于张量分解的个性化推荐算法研究[D].南昌：华东交通大学，2018.

（编辑 何 琳）