联合仿真模型中的插值方法分析与实验
2021-09-13蒋洋杨建常
蒋洋 杨建常


摘 要:随着现代科技的进步与发展,计算机仿真的研究深度也在不断扩展,其复杂性也日益增加,采用的工程软件越来越多、不同种类的工程数据格式也越来越多。此时FMI功能模拟接口标准的横空出世,将不同软件工具建立的仿真工程相互连接起来。在仿真过程中对模型间数据交互进行分析,发现存在不同步长FMU模型数据交互情况,此时需要通过插值算法来减少结果误差。该文通过牛顿插值法和三次样条插值法进行内插实验,对这两种插值方法进行比较,分析其适用性。
关键词:FMI联合仿真 数据交互 牛顿插值 三次样条插值
中图分类号:TP393.07 文献标识码:A文章编号:1672-3791(2021)06(a)-0001-03
Analysis and Experiment of Interpolation Method in
Co-simulation Model
JIANG Yang1 YANG Jianchang2
(1.Shenyang Ligong University, Shenyang, Liaoning Province, 110159 China; 2.Unit 32683, Shenyang, Liaoning Province, 110043 China)
Abstract: With the progress and development of modern science and technology, the research depth of computer simulation is also expanding, its complexity is also increasing, more and more engineering software and different types of engineering data formats are used. At this time, the FMI functional simulation interface standard was born, connecting the simulation projects established by different software tools. In the simulation process, the data interaction between models is analyzed, and it is found that there is FMU model data interaction with different steps. So interpolation algorithm is needed to reduce the result error. In this paper, Newton interpolation and Cubic spline interpolation method are used for interpolation experiments, the two interpolation methods are compared and their applicability is analyzed.
Key Words: FMI co-simulation; Data interaction; Cubic spline interpolation; Newton interpolation
隨着时代发展,建模与仿真技术越来越注重系统与模型的联合开发,在仿真上可实现多种学科的联合应用、多种仿真环境的集合以及多种仿真过程的结合[1]。除此之外,为使各模型间的数据可以正常传输处理,以及满足不同模型的系统需求,需要通过标准的接口协议来对不同领域、不同层次的模型进行集成处理。FMI功能模拟接口标准因此应运而生[2]。然而在仿真过程中,不同步长的FMU模型间可能会出现数据丢失以及仿真结果不精确的问题[3]。这一问题可通过使用插值方法对仿真结果行优化处理来解决。
该文主要描述针对仿真中牛顿插值法以及三次样条插值法进行内插的分析与实验,对这两种常见的插值方法进行比较,分析其适用性,得出结论。
1 插值法
插值是指已知某函数的在若干离散点上的函数值,通过求解该函数中待定形式的插值函数以及待定系数,在区间的其他点上用这特定函数的值作为函数f(x)的近似值。不同的插值方法求得多项式的方式不同。
1.1 牛顿插值法
牛顿插值法引入了差商的概念,大大减少了计算量,提高了计算精度[4]。同时,在添加或更新节点时,牛顿插值也具有承袭性,计算更为灵活[5]。已知函数f(x)在n+1个互不相同点处的函数取值为f(xi),高阶差商与低阶差商存在迭代关系。
f(x)在点xi,xj处的一阶差商为:
xi,xj处的一阶差商为
二阶差商是一阶差商的差商,f(x)在点xi,xj,xk处的二阶差商为:
(2)
三阶差商就是二阶差商的差商,以此类推,f(x)在点x0,x1,…xn处的n阶差商为:
(3)
牛顿插值法的基本表现形式为:
f(x)=f(x0)+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x- x1)+…+f[x0,x1,…xn-1,xn](x-x0)(x-x1)…(x-xn-1)
(x-xn)(4)
1.2 三次样条插值
有学者发现随节点个数n的增加,多项式误差不但没减小,反而不断增大。人们把这种节点加密但误差增大的现象称为Runge现象。该文的分段三次样条插值就是克服Runge现象引入的一种插值方法[6]。
顾名思义,分段就是把整区间分成n个区间[(x0, x1), (x1, x2), …(xn-1, xn)],共有n+1个点,其中两个端点x0=a, xn=b,三次样条就是说每个小区间的曲线是一个三次方程,三次样条方程满足以下条件。
(1)在每个分段小区间[xi, xi+1]上,S(x)=Si(x)都是一个三次方程。
(2)满足插值条件,即S(xi)=yi (i=0, 1, 2, …, n)。
(3)曲线光滑,即S(x),S'(x),S''(x)连续。
则这个三次方程可以构造成如下形式:
y=ai+bix+cix2+dix3(5)
这种形式下,称这个方程为三次样条函数[7]。
从公式(5)可以看出每个小区间有4个未知数,有n个小区间,则有4n个未知数,要解出这些未知数,则需要4n个方程来求解。
首先,由于所有点必须满足插值条件S(xi)=yi(i=0, 1, …, n),除了两个端点,所有n-1个内部点的每个点都满足Si(xi+1)=yi+1,Si+1(xi+1)=yi+1前后两个分段三次方程,则有2(n-1)个方程,再加上两个端点分别满足第一个和最后一个三次方程,則总共有2n个方程。
其次,n-1个内部点的一阶导数应该是连续的,即在第i区间的末点和第i+1区间的起点是同一个点,它们的一阶导数应该也相等,即S'i(xi+1)= S'i+1(xi+1),则有n-1个方程。另外,内部点的二阶导数也要连续,即S''i(xi+1)=S''i+1(xi+1),也有n-1个方程,现在总共有4n-2个方程了,还差两个方程就可以解出所有未知数了,这两个方程可通过边界条件得到。
该文算法设计使用固定边界条件(指定端点一阶导数),这样即构造方程组解出所有未知数。
2 基于python的仿真方法设计
2.1 牛顿插值法的设计流程
(1)输入真实离散数值,插值点范围及个数。
(2)调用函数获取差商表。
(3)调用函数获取差商表的对角线元素。
(4)设计newton函数,输出结果。
2.2 三次样条插值法的设计流程
(1)输入真实离散数值,插值点范围及个数。
(2)计算步长,将数据节点和指定的首位端点条件带入矩阵方程。
(3)解矩阵方程,计算样条曲线的系数。
(4)在每个子区间创建方程,输出结果。
3 仿真结果与分析
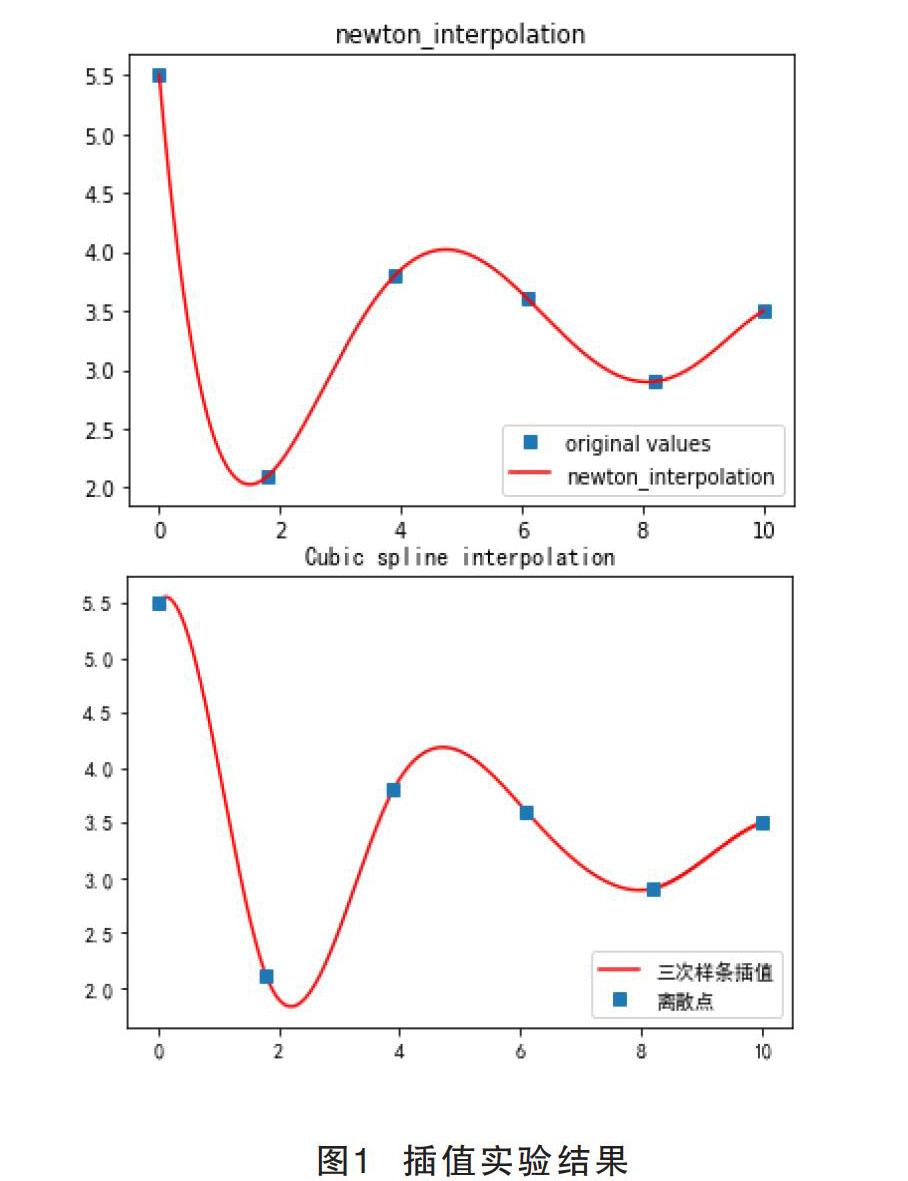
分别对牛顿插值法和三次样条插值法进行实验,得到结果见图1。其中图中小方块点代表真实值,曲线为插值拟合曲线。
由实验结果可看出,两种插值方法得到的插值曲线较为接近,随机取插值点得到的结果也误差较小。但由于分段三次插值可以低代价获得一阶和二阶导数的收敛性质,插值曲线更逼近真实曲线,因此当插值节点较多的情况下,可优先考虑三次样条插值法。
4 结语
随着联合仿真技术的飞速发展,工程人员在设计验证相关产品时更方便快速。该文分析比较了牛顿插值法和三次样条插值法的不同之处,对于仿真过程中不同步长的FMU模型间可能会出现仿真结果不精确的问题进行优化处理,具有一定的应用价值。
参考文献
[1] 罗茂春.基于FMI的航空发动机控制系统多学科联合仿真[D].南京:南京航空航天大学,2019.
[2] 樊卿.基于FMI的飞行器联合仿真技术研究[D].成都:电子科技大学,2018.
[3] 胡嘉悦,李广文,章卫国,等.面向有人/无人机协同远程作战的IVMS架构[J/OL].航空学报:1-12[2021-05-19].https://www.kns.cnki.net/kcms/detail/11.1929.V.20210326.1703.022.html.
[4] 李振昌.基于卫星星历的BDS卫星轨道插值与拟合方法研究及精度分析[D].兰州:兰州交通大学,2019.
[5] 杨伟.基于牛顿插值法的模拟信号采样与重构研究[D].兰州:兰州大学,2017.
[6] 李文.移动机器人路径规划的改进粒子群三次样条插值算法[D].湘潭:湘潭大学,2020.
[7] 魏媛.模糊三次样条插值与模糊最小二乘逼近[D].兰州:西北师范大学,2020.
