基于序列模式的业务流程模型的预测对
2021-09-13齐陈荣
齐陈荣


摘 要:为突破固定模式,实时预测,使流程管理更高效更准确,本文提出一种基于序列模式的对齐预算方法。以业务流程模型和日志集作为输入,通过分析模型中活动的行为关系,将活动划分为不同的序列模式,利用条件概率对序列模式中活动做预测。并且通过实例分析了该方法的有效性。
关键词:Petri网;对齐;预测;序列模式;条件概率
中图分类号:TP391.9 文献标识码:A 文章编号:1673-260X(2021)07-0013-04
0 引言
随着信息技术的快速发展,业务流程管理在企业或组织间扮演着越来越重要的角色。然而,真实的业务场景与流程模型间会存在行为不一致,我们经常使用对齐来描述这种差异。目前,国内外很多学者研究了对齐问题。例如,Bloemen V等[1]提出了不同于标准成本函数的新的成本函数,设计了优先考虑最大化同步移动对齐算法,该算法不同于A*算法和符号算法,最后通过实例说明了算法的实用性和有效性。Garcia-Banuelos L等[2]介绍了一种新的对齐方法,即通过两个事件结构做纠错同步积的对齐方法,并详细阐述了日志与模型间的六种不匹配行为,通过一种自然语言来描述这个变化。刘静[3]等人提取出事件日志有效的高频形态学发生片段,在此基础上发现最优迹对齐。前人在对齐方面的研究,大多是通过暴力搜索来寻找差异且日志与模型都具有完整性。因此,突破固定模式,实时预测,使流程管理更高效更准确显得尤为重要。关于预测的研究有,Tax N等[4]提出了一种基于机器学习方法预测在给定的不完整序列之后可能出现的元素。Hamed R I[5]提出了一种基于模糊规则推理的模糊Petri网方法,通过实验表明所提出的模型可以达到与现有软件相匹配的置信值。Ma Z等[6]利用极小值和可达图解决了有标识Petri网中的一个基本标识估计问题,提出了基础标识的两种概念,并证明对于一组警报是可预测的。
基于上述研究,本文提出了一種基于序列模式的业务流程模型的预测对齐方法。第1节通过动机例子引出本文方法;第2节介绍相关定义;第3节首先将活动划分为三个序列模式,提高对齐效率。然后,利用条件概率预测下一节点的发生;第4节进行实例分析;最后总结全文并展望未来。
1 动机例子
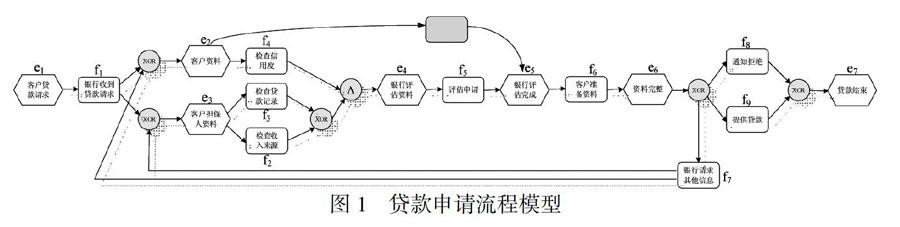
本节将利用某贷款申请流程来说明本文的研究动机,为了方便起见,将每个函数赋予新的标签如表1所示,图2是用EPC(事件驱动过程链)语言描述的贷款申请流程。流程从“银行收到贷款申请”开始,两个任务“检查信用度”和“检查收入来源”或“检查信用度”和“检查贷款记录”并发,进入“评估申请”环节,或者直接进入“客户准备资料”环节,然后两个分支选择发生“提供贷款”或者“通知拒绝”,最后以“贷款结束”完成整个贷款流程。
考虑日志L={ACFI,AEFGI},常见的两种对齐方式有基于A*最短路径算法的最优对齐和最大化同步移动对齐。我们认为这两种对齐方法并不总是合适的,(1)A*算法旨在以暴力搜索的方式寻找最短路径以达到成本最低的对齐如γ1,可以看出通过跳过活动C以达到成本最低,但在真实业务场景中,无法判定活动C是否应该发生,若活动C发生如γ2。(2)最大化同步移动对齐旨在尽量使日志与模型对齐以减少跳过移动,进而达到成本最低如γ3,在模型中活动G是进入循环的标志性活动,若进入循环体如γ4。针对这两种问题,本文提出一种基于序列模式的预测对齐方法,这种方法不仅能预测下一个发生的节点,还能更高效更准确地进行预测。
2 基本概念
定义1[7,8](业务流程Petri网) 一个网PN=(P,T;F)是业务流程Petri网,当其满足以下条件:
(1)P为库所集,有P≠?覫。
(2)T为变迁集,有T≠?覫。
(3)F=(P×T)∪(T×P)为流关系集。
在流程模型P的变迁之间存在一种弱序关系,即一对变迁(x,y)∈T×T是弱序关系,当且仅当存在一个发生序列?滓=t1t2…tn有(P,M0)[?滓〉,并且有i,j∈N,1≤i≤j≤n使得tj=x,ti=y,记作x?酆y。根据弱序关系定义模型和日志的行为轮廓关系[9]。
定义2[10](模型的行为轮廓) 设P是一个流程模型,对?坌(x,y)∈P,则x,y的行为关系如下:
(1)严格序关系→P,若x?酆Py∧y≯Px,记作x→Py。
(2)交叉序关系||P,若x?酆Py∧y?酆Px,记作x||Py。
(3)排他序关系+P,若x≯Py∧y≯Px,记作+Py。
则称集合BP{→P,||P,+P}是模型P的行为轮廓。
定义3[11](序列模式) 流程模型P中的所有活动集A,序列?籽=
定义4(依赖关系) 序列模式?祝=<<?琢1,?琢2,…,?琢k>,<?茁1,?茁2,…,?茁k>,<?酌1,?酌2,…,?酌k>>=<?琢i,?茁i,?酌i>,其中i=1,…,k。
?坌?琢k∈A,?埚?琢k∈?茁i,?酌i,st.?琢k?埸L,其中?琢i为长期依赖关系集,?茁i为长期冲突关系集,?酌i为长期选择关系集,L为日志。
如图2所示,活动a和活动g处于干路,即此活动必须出现在任意一条发生序列上,我们将其称为长期依赖关系。然而,活动e和活动f只能有一个出现在发生序列中,即存在长期选择关系,而活动h和活动i则不能同时出现在一条发生序列中,所以,两者呈长期冲突关系。理解活动集合的划分不仅是预测的基础,还能通过划分模型提高对齐效率。
3 序列模式的预测对齐
序列模式旨在分解流程,将流程模型中的活动按行为关系划分为三个集合,即?祝=<?琢i,?茁i,?酌i>。在三个关系集合中,首先对齐?琢i中的集合,即长期依赖关系优先对齐;然后,在已对齐的活动中利用条件概率预测在集合?茁i中需要对齐的活动;最后,在冲突集合?酌i中找出与已对齐活动呈冲突关系的其他活动将其跳过。
算法1 (序列模式的划分)
输入:输入流程模型P、日志的发生序列L=[li]。
输出:基于序列模式的对齐li?苁。
(1)输入流程模型P,将流程模型中的活动划分为三个活动集合?琢i、?茁i、?酌i,执行步骤(2)。
(2)从日志中选择一条发生序列li,首先对齐在?琢i集合中的活动得到序列li′;然后以已对齐的活动为条件利用条件概率在?茁i集合中预测需要对齐的活动得到序列li″;最后在集合?酌i中找出与已对齐活动呈冲突关系活动,执行步骤(3)。
(3)将冲突的活动直接跳过,输出一条基于序列模式的预测对齐序列li?苁,算法结束。
由于算法2是在条件概率的基础上进行的,因此,我们先引入条件概率定义。
定义5 (条件概率) 设A,B是两个事件,且P(B)>0,P(A/B)为事件B发生的条件下事件A发生的条件概率。当B={B1,B2,…,Bn},Bn≠?覫时,条件概率公式为P(A)=∑,有,P(A)=1-P(A)。
算法2 (基于条件概率的预测)
输入:流程模型P、序列li′和集合?茁i。
输出:集合?茁i中需要对齐的活动。
(1)输入流程模型P和发生序列li′,执行步骤(2)。
(2)利用定义5的条件概率来判定集合?茁i中需要对齐的活动,执行步骤(3)。
(3)将序列li′中已对齐的活动作为条件,如果在此条件下该活动的发生概率大于1/2,则对齐该活动;如果在此条件下该活动不发生的概率大于1/2,则对齐与该活动成选择关系的活动,算法结束。
4 案例分析
算法1和算法2详细阐述了如何利用条件概率预测下一节点的发生,通过划分序列模式,提高了对齐效率。本节将通过一个实例具体分析算法中所提到的方法,由于本文以EPC语义为背景,首先利用方贤文[12]提出的EPC诱导方法将其转化为Petri网,如图3。
考虑日志l1=ABCEFI,首先利用算法1将流程模型划分为三个集合,?琢i=
5 结束语
本文提出了一种基于序列模式的业务流程模型的预测对齐方法,它以流程模型和日志发生序列作为输入,通过划分序列模式将活动分成三个关系集。随后利用条件概率在已对齐活动的情况下预测下一节点发生的概率。该方法打破了以成本和路径为基础的常规对齐方法,并提高了对齐效率,已进行的实例评估验证了该方法在实践中的适用性和可扩展性。
然而,我们的方法也有一定的局限性,它主要限制于有界的流程模型和完整的日志序列,对于无界的流程和序列,我们无法判断。在未来工作中,需要对预测做进一步研究,并将其应用于Prom框架中。
参考文献:
〔1〕Bloemen V, Zelst S J V, Aalst W M P V D, et al. Maximizing Synchronization for Aligning Observed and Modelled Behaviour: 16th International Conference, BPM 2018, Sydney, NSW, Australia, September 9-14, 2018, Proceedings[M]// Business Process Management. 2018.
〔2〕Garcia-Banuelos L, Van Beest N, Dumas M, et al. Complete and Interpretable Conformance Checking of Business Processes[J]. IEEE Transactions on Software Engineering, 2015:1-1.
〔2〕Luciano Garcia-Banuelos,Nick R T P van Beest,Marlon Dumas,et al. Complete and interpretable conformance checking of business processes[J]. IEEE Transactions on Software Engineering, 2018, 44(03):262.
〔3〕刘静,方贤文.基于成本对齐的业务流程变化挖掘方法[J].计算机科学,2020,47(07):78-83.
〔4〕Tax N, Teinemaa I, Zelst S. An interdisciplinary comparison of sequence modeling methods for next-element prediction[J]. Software and Systems Modeling, 2020, 19(02).
〔4〕Tax N, Teinemaa I, Zelst S. An interdisciplinary comparison of sequence modeling methods for next-element prediction[J]. Software and Systems Modeling, 2020, 19(02).
〔5〕Hamed R I. Confidence value prediction of DNA sequencing with Petri net model[J]. Journal of King Saud University ¨c Computer & Information Sciences, 2011, 23(02):79-89.
〔6〕Ma Z, Yin X, Li Z. Marking Predictability and Prediction in Labeled Petri Nets[J]. IEEE Transactions on Automatic Control, 2020, PP(99):1-1.
〔7〕應丽,方贤文,王丽丽,刘祥伟.基于业务能力的可配置业务流程模型变化域分析[J].计算机科学,2019,46(10):322-328.
〔8〕吴哲辉.Petri网理论[M].北京:机械工业出版社,2006.6-42.
〔9〕郝晋渊,孙丹丹,郝真鸣,陈凡,冉宁.基于标签Petri网的自动制造系统初始资源配置优化[J].电子测量与仪器学报,2020,34(08):30-36.
〔10〕郝惠晶,方贤文,王丽丽,刘祥伟.基于Petri网行为紧密度的有效低频行为模式分析[J].计算机科学,2019,46(02):321-326.
〔11〕M. Fani Sani, S.J. van Zelst, and W.M.P. van der Aalst. Applying Sequence Mining for Outlier Detection in Process Mining[J]. 2018.
〔12〕方贤文,彭珂,王丽丽,等.基于配置和撤销状态的业务流程变化传播分析[J].计算机集成制造系统,2018,24(07):1621-1630.
