基于改进BP神经网络的音乐流派分类

摘  要：针对传统音乐流派分类模型性能不稳定、音乐信号特征单一导致分类准确率低的问题，提出了改进的BP神经网络（Back Propagation Neural Network）音乐流派分类模型，通过Python的Librosa库提取了音乐的均方根能量、过零率、频谱质心、频谱对比度等多种特征，并使用PCA（Principal Component Analysis）和LDA（Linear Discriminant Analysis）数据降维方法对特征数据进行可视化分析，证明了特征选取的合理性。最后对四类音乐流派进行仿真实验，并与传统的分类模型对比。实验证明，提出的模型10 折交叉验证的准确率为93.12%，优于KNN（K-Nearest Neighbor）、SVM（Support Vector Machine）等传统的分类模型。

关键词：机器学习;特征提取;支持向量机;梅尔频率倒谱系数

中图分类号：TP39     文献标识码：A

文章编号：2096-1472（2021）-09-17-04

Abstract： Classification models of traditional music genre have problems of unstable performance and low classification accuracy caused by single characteristics of music signals. In view of these problems， this paper proposes an improved BP （Back Propagation） Neural Network music genre classification model. Various features such as root mean square energy， zero crossing rate， spectral centroid， and spectral contrast of music are extracted through the Librosa library of Python. Then， visual analysis of the feature data using PCA （Principal Component Analysis） and LDA （Linear Discriminant Analysis） data dimensionality reduction methods has proved the rationality of feature selection. Finally， simulation experiments are conducted on four types of music genres， and compared with the traditional classification model. The experiment proves that the accuracy of the 10-fold cross-validation of the model proposed in this paper is 93.12%， which is better than traditional classification models such as KNN （K-Nearest Neighbor） and SVM （Support Vector Machine）.

Keywords： machine learning; feature extraction; SVM; MFCC

1   引言（Introduction）

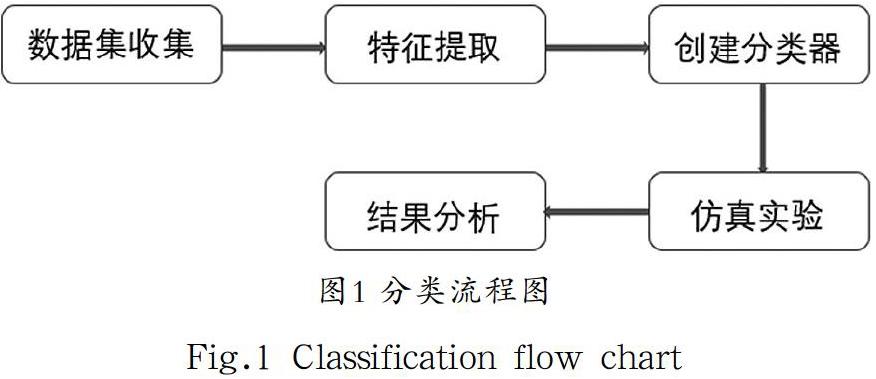
随着多媒体技术的发展，音乐以各种方式出现在人们身边，面对网络上海量的音乐，不同的人喜好差异较大，为方便检索，对音乐流派进行分类尤为重要。庄严[1]等人提出了一种基于谱图分离的音乐流派分类算法，通过对音乐信号的谱图滤波，分离出音乐的打击与和声部分，对特征进行优化，通过SVM分类器对8 种音乐流派进行仿真实验，最终达到73%的准确率。陆欢[2]则采用梅尔频率倒谱系数（Mel-Frequency Cepstral Coefficients， MFCC）特征矩阵作为音乐信号的特征，训练了卷积神经网络作为分类器，在4 种音乐流派上得到88%的结果。本文借助于Python的Librosa库，研究了音乐信号的某些时域特征和频域特征，选取了过零率、均方根能量、频谱质心、滚降截止频率、频谱对比度、梅尔频率倒谱系数作为音乐数据集的特征，有效解决了单一特征造成的分类准确率低的问题。最后借助机器学习的工具，建立了一个4层的BP神经网络模型，实现了有效分类。音乐流派分类主要流程如图1所示。

2  数据处理和特征提取（Data processing and feature extraction）

2.1   数据集

本文中使用的数据集是公开的GTZAN数据集[3]，该数据集包含10 种音乐流派，每种流派各有100 段时长为30 秒，采样频率为22.05 kHz的16 bit的数字信号。本文选取了布鲁斯（bules）、古典（classical）、乡村（country）、金属（metal）共4 种音乐流派，共400 个样本。

2.2   特征提取

语音信号具有短时平稳性，即在一个短時间范围（10 ms—30 ms）内，其特性基本保持不变，因此，对于语音信号的分析都是建立在“短时”的基础上[4]。在提取语音信号的特征时，首先对信号进行分帧加窗处理，特征提取函数的返回值是每一帧上的结果，选取每个特征在所有帧上的平均值和方差作为该文件的特征，这样，对于一个音频文件，提取出来的特征向量的维度是46。特征提取在音乐流派分类中占有非常重要的地位，针对单一特征导致分类准确率低的问题，本文基于Python中的Librosa库提取了过零率、均方根能量等多种特征[5]，特征名称及其维度如表1所示。

（1）过零率是信号相邻两个采样点取值为异号的次数，它可以对敲打的声音进行区分[6]。

（2）均方根能量是每一帧内采样点能量的标准差，可以用来区分有声和无声，轻音和浊音[1]。

（3）频谱质心是用来表征频谱的度量，表示“质心”的位置，与声音的亮度有关，值越小，说明越多的能量集中在了低频的范围内。图2（a）和图2（b）分别展示了blues和metal两种不同流派的音乐频谱质心的位置，可以看到，相比于metal，blues的频谱质心“更低”，且能量主要在低频范围。

（4）滚降截止频率是谱形状的重要测度，85%的幅度分布低于该频率[6]，表示能量大幅上升（或大幅下降）、失去“阻止”（或失去“通过”）信号效果的位置。

（5）频谱对比度是信号的幅度谱在每个子波段上峰值与峰谷平均能量的差，高对比度值通常对应于清晰的窄带信号，而低对比度值对应于宽带噪声。

（6）梅尔频率倒谱系数是语音信号处理中被广泛使用的

特征，由于人耳听到声音的高低与声音的频率之间的关系并不是线性关系，频率尺度更符合人耳的听觉特性[4]，频率与实际频率之间的关系可以表示为：它的计算方式在文献[4]中都有详细描述，这里不再赘述。

2.3   特征数据的降维分析

数据降维方法有多种，线性降维算法因其实现简单快速的特点应用广泛，主成分分析（PCA）和线性判别分析（LDA）是线性降维中两种经典的算法。实验中，分别使用PCA和LDA对提取的46维特征数据进行降维分析，并将其可视化，图3为PCA降维的结果，图4为LDA降维的结果。

从图3中可以看到，通过PCA算法将46 维特征降为2 维后，classical和metal可以被很好的分开。与PCA不同的是，LDA在计算类内散度和类间散度时应用了数据的标签[7]，因此LDA是一种有监督的降维方法。从图4中可以看到，经过LDA降维，特征数据被分成了较为明显的四类，其中，classical、country和metal分类效果较好，从而反映出本文特征选取的合理性。

3  基于正则化的BP神经网络（BP neural network based on  regularization）

3.1   神经网络基础

BP（Back Propagation）神经网络是1986 年由Rumelhart和McClelland为首的科学家提出的，它是基础的也是目前应用最广泛的神经网络之一。图5展示了具有两个隐藏层的神经网络结构图。

信号通过输入层、隐藏层、输出层前向传播得到预测值，利用损失函数衡量预测值与真实值之间的误差，从最后一层反向传播误差[8]，通过适当的优化器，比如梯度下降，随机梯度下降等更新权重参数和偏置参参数，最小化误差，从而使预测值与真实值更接近。神经网络中前向传播和反向传播的伪代码如表2和表3所示。

其中，是由样本数据为行向量组成的输入矩阵，代表神经网络的层数，表示第层神经网络的输出，是激活函数，是层到层的权重矩阵，，表示样本的真实标签组成的向量，表示梯度下降的学习率，表示哈达玛积（Hadamard Product），即对于向量，

3.2   网络结构

本文设计的神经网络包含3 个隐藏层，神经元的个数分别为128、64、32。ReLU激活函数又称为修正线性单元，表达式为，由于其具有单侧抑制，稀疏激活等优点，故选其作为隐藏层的激活函数。选择多分类对数损失作为损失函数，如果目标值为时预测结果为，分类的交叉熵为：。优化器则选择随机梯度下降，这是因为相比于普通的梯度下降算法，随机梯度下降的收敛速度更快。本文研究的是四分类问题，所以输出层的神经元个数为4，输出层的激活函数为Softmax函数。由于本文的数据量较少，并且样本的特征差异不大，为了防止过拟合，在设计神经网络结构时加入正则项，因此优化模型可以表示为：

其中，是损失函数，是权重矩阵的列向量，为正则项，为正则化系数。经过多次调试，最终确定正则化系数为0.004。图6展示了增加正则项与未增加正则项时模型在训练集和测试集上准确率和损失值随着每期训练的变化曲线（图6（a）和图6（c）为增加正则项后曲线图，图6（b）和图6（d）为未增加正则项曲线图）。从图6（a）和图6（b）中可以看出，模型在训练集上表現较好，准确率达到1，而增加正则项后，无论是测试集上的准确率还是损失值变化曲线都更贴近训练集，且经过300 期训练后准确率略微有些提高。

4  实验结果与分析（Experimental results and analysis）

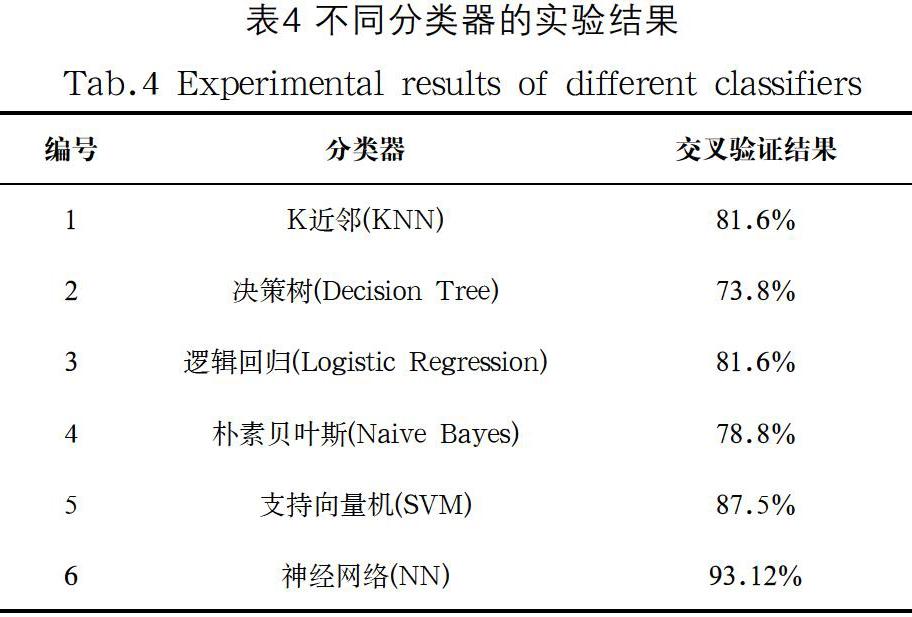
本文按照4∶1的比例划分训练集和测试集，从总样本中选取80 个样本组成测试集，其中每种音乐流派各20 个。剩余320 个样本作为训练集，在训练集上进行10 折交叉验证，即将训练集分成10 个非重叠的部分，每次选其中一部分作为验证集，其余9 部分作为训练集。共进行10 次训练，选取模型在验证集上10 次准确率的平均值为模型最终得分。具体分类结果如表4所示，可以看到，除决策树外，其他模型的准确率均在80%左右，本文建立的神经网络模型（NN）得到的准确率最高，达到93.12%。

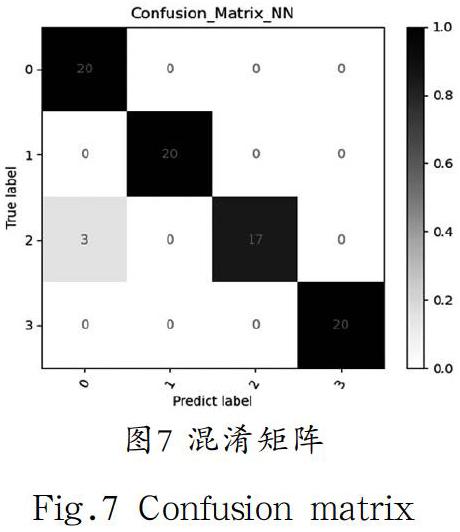
接下来分析模型对每种音乐流派具体的分类结果，我们绘制出模型在测试集上的混淆矩阵如图7所示，其中0代表blues，1代表classical，2代表country，3代表metal。横坐标轴表示的是预测类别的标签，纵坐标轴代表的是真实类别的标签。该模型对blues、classical和metal三种流派能做到精准分类，对于country的区分效果相对较差，误将3 个country类别的文件识别成了blues，我们猜想原因与所提取的特征不能有效将这两种音乐类别区分有关，图3和图4可视化的结果也验证了这一点。

5   结论（Conclusion）

音乐流派分类作为音乐信息检索领域比较热门的方向，涉及信号处理、模式识别、计算机、数学等多门学科，引起众多学者的研究，无论是在特征提取还是分类器的选择上都提出了许多新方法。本文选取的音乐特征虽能够对不同流派的音乐进行区分，但也存在一定的不足，需要寻求更多特征以保证分类的准确率。其次，本文建立的神经网络分类模型在四分类上有不错的表现，但是当音乐种类增多时，分类效果会有一定程度的下降，需要在模型上做进一步的优化。

参考文献（References）

[1] 庄严，于凤芹.基于节奏和韵律调制谱特征的音乐流派分类[J].计算机工程，2015，41（1）：186-189.

[2] 陆欢.基于卷积神经网络的音乐流派分类[J].电子测量技术，2019，42（21）：149-152.

[3] TZANETAKIS G， COOK P. Musical genre classification of audio signals[J]. IEEE Transactions on Speech and Audio Processing， 2002， 10（5）：293-302.

[4] 赵力.语音信号处理[M].北京：机械工业出版社，2016：6-84.

[5] 张俊生，郭彩萍，楼国红，等.Python在数字信号处理中的应用[J].电气电子教学学报，2015，37（04）：115-117.

[6] 黄琦星.基于卷积神经网络的音乐流派分类模型研究[D].长春：吉林大学，2019.

[7] 赵玉娟.数据降维的常用方法分析[J].科技创新导报，2019，32（16）：118-119.

[8] NIELSEN M. Neural networks and deep learning[M]. San Francisco： Determination Press，2015：34-109.

作者简介：

樊思含（1995-），女，硕士生.研究领域：机器学习，计算数学.