非线性分类模型在高速公路边坡监测中的应用

陶 虎

(广西交投科技有限公司，广西 南宁 530000)

0 引言

高速公路边坡是破坏主体自然结构并对其进行防护形成的人造结构，沿线边坡极易受到地质条件和环境因素的影响而失稳，造成滑坡、塌方、落石等灾害，对沿线公路造成巨大的破坏，对通行车辆和人员的安全造成严重威胁。因此在高速公路边坡监测中，如何准确有效预测边坡形变发生，掌握边坡的地质变化和发展趋势，是高速公路养护管理部门在灾害发生前提前做好边坡防护防治、交通警示疏导等措施，减少人员财产经济损失的关键。

高速公路边坡监测的实际目的是进行边坡形变预测，对边坡形变后期的发展做出及时、准确的预判[1]。边坡的形变发展是从蠕动、快速滑动到滑坡的过程，此过程中一些可监测的地质参数(例如边坡位移量、地声、应力、地下水量位等)也会随之变化。地质参数变化受多重因素影响，存在非线性和不确定性，如何利用地质参数进行有效、准确的边坡形变计算预测是非常必要的。

目前，边坡形变计算预测方法主要有两类[2]：(1)定性分析法，通过综合参考边坡周边的各种影响因素，及时评判边坡形变趋势，分析预测其发展变化，典型的方法有工程地质条件比对法和地质参数因子分析法；(2)定量分析法，对地质形变参数采用数学统计、模糊综合评判模型或非线性分类模型等方法进行计算，以获得形变趋势预测数据。目前边坡形变预测没有存在普适性的方法。依据边坡的地质条件和气候环境，建立合适的边坡形变计算预测模型对边坡形变进行有效预测，是边坡监测工作的关键内容。

本文针对广西地区特有的地质条件和气候环境，依托泉南高速公路柳州至南宁段监测项目，应用具备分析非线性和不确定性分类问题的模糊神经网络模型和支持向量机算法对边坡地质参数进行计算，获取地质参数与边坡形变安全系数的拟合回归函数，以获得边坡形变安全系数的变化趋势，判断边坡安全性，为边坡防护防治提供科学依据。

1 非线性分类算法模型

1.1 支持向量机算法模型

支持向量机(support vector machines，SVM)是基于VC维理论[3-4]和追求结构化风险最小原理[5]逐步发展而来的机器学习算法。在统计样本量较少的前提下，能够获得十分出色的统计规律模型[6]。在非线性分类模型中分类问题，假设样本集：(Xi，yi)(i=1，2，3，…，N，y∈{-1，1})，X∈Rn，其中参数y确定正负样本子集X+、X-，能将样本由原始的低维度空间映射到高维度空间，使样本集在维度特征空间具有线性可分的特征。SVM的数学模型中希望得出一个拟合函数f(x)使其分类样本尽可能接近真实情况。这个模型中以f(x)为中心构造一个距离为γ间隔的分类平面，如图1所示。

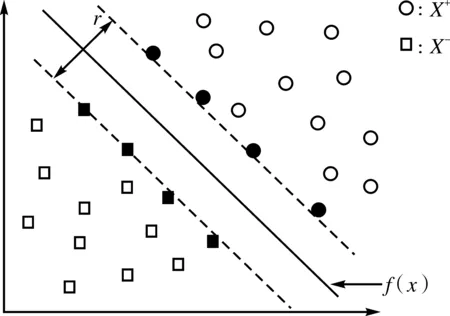
图1 最优分类超平面示意图

设一个变量w*和一个常量c*，则约束式拟合函数可写成判别函数形式：

(1)

其中式(1)向量w*具有最小范数：

(2)

引入松弛变量(ξi，ξi*)，优化判别目标公式为：

(3)

(4)

引入Lagrange乘子法求解二次规划问题，Lagrange方程式为：

(5)

根据目标函数的约束条件可以得到支持向量机的拟合函数为：

(6)

为了将非线性分类通过特征空间映射到高维度特征空间中进行线性问题求解，因此引入了核函数K(Xi，Xj)代替线性问题中的内积运算：

(7)

1.2 模糊神经网络模型

模糊神经网络(FuzzyNeuralNetwork，FNN)模型是综合了模糊系统和神经网络的互补优势性，使该模型具有自主学习、自动识别、自适应模糊化处理等优势。该模型主要思想为对神经网络输入信号模糊化处理，将其转化为模糊系统的输入信号和权值。在FNN模型中，实现学习和优化权值系数是算法的关键。而基于网络自适应模糊神经系统(AdaptiveNetwork-basedFuzzyInferenceSystem，ANFIS)则融合了神经网络学习算法和模糊系统的推理优势，其原理是给定输入/输出的数据集，构造出模糊网络模型(支持T-S型系统)[7]，利用最小二乘法和单独反向传播对系统隶属函数的参数进行调节。ANFIS模型网络结构主要有输入/输出的变量和空间划分，判断规则条数和隶属度函数个数等部分，它可以对模型的可调整参数进行调整，以此来得到最佳输出[10]。模糊神经网络的典型结构如图2所示。

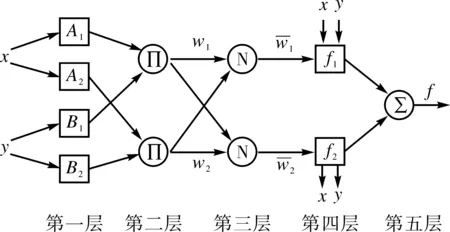
图2 模糊神经网络结构图

在构造模糊网络模型过程中，将原有模型转化为自适应网络模型，从而建立T-S型系统的模糊学习过程。自适应网络模型为多层的前馈网络结构。网络的输入层主要是将输入信号模糊化，该层为输入变量的隶属函数层，节点i的输出函数为：

(8)

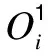
嘉善田歌是民歌艺术的一种特殊表现形式，归属于口传类非物质文化遗产。它们都是口口相传，并没有物质性和符号性载体，跟随着传承者生而生亡而亡。因此，保护传承者，对此类非物质文化遗产的保护传承就显得尤为重要了。传承者，即继承、操纵和创作嘉善田歌的歌手和民间艺人等，是传承主体的核心。而传播者和接受者可以被定义成传播嘉善田歌音乐文化的社会个体或群体，它们可能是一个人，也有可以是一个组织团体，如文化企业、公益社团、媒体和政府等。

首层主要是把模型训练的评价质变数据传播到下一层[8]。第二层是对上层传递的信号进行乘积运算，结果输出得到每条规则的适用度，可表达为：

(9)

式中：每个节点i的输出代表第i条规则的可信度。

第三层是对每条规则的适用度归一化处理，第i个节点计算第i条规则的ωi占全部规则ω之和的比值为：

(10)

第四层是计算模糊规则输出，每个节点i均为自适应节点，其输出结果为：

(11)

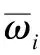
第五层是固定节点，是汇总所有输入信息计算总输出：

(12)

ANFIS的输出结果可在确定前件参数基础上使用后件参数的线性组合表示[12]：

(13)

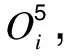
2 监测数据

高速公路边坡地质稳定性的影响因素多样，但在实际边坡监测中边坡形态的不稳定性发展主要是由内摩擦角φ、重度参数γ、粘聚力c、边坡角度α、边坡滑动面与坡面高度H、空隙水压力ρ等边坡截面结构因素共同作用造成的[9]。因此本文选取主要影响边坡地质稳定性因子的实时监测数据，应用非线性分类模型算法计算各参数与边坡形变安全系数A的拟合回归函数，获得A的变化趋势，来判断边坡的安全性。高速公路上常见的边坡截面结构如图3所示。

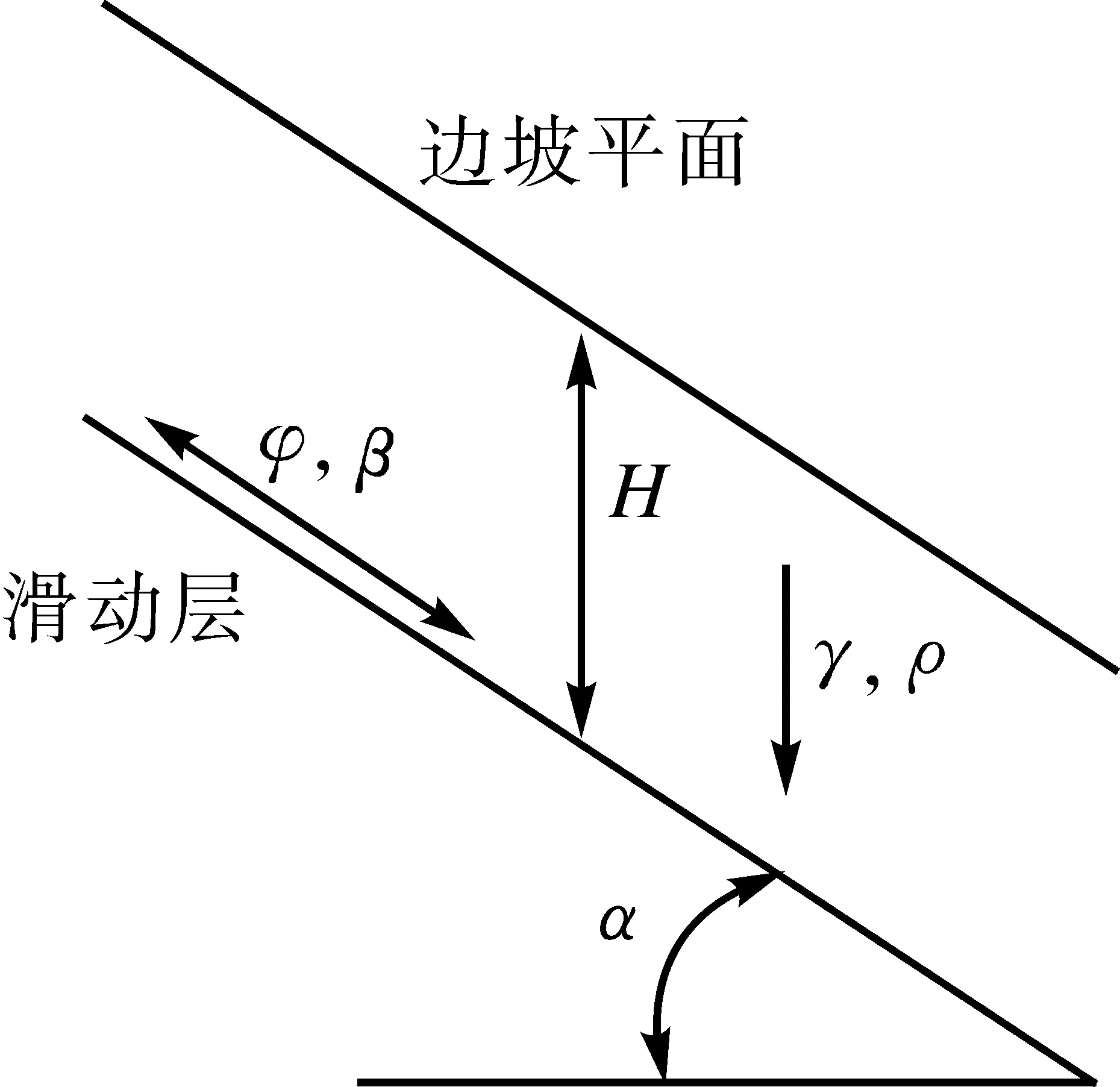
图3 边坡截面结构模型示意图

预测模型的性能与训练样本密切相关，训练样本需考虑样本长度与全面性。它们直接影响着模型学习速度、仿真能力以及能否全面反映监测参数与A的因果关系。A划分为3个等级即稳定、变形、滑坡，并分别赋予值A∈(1，2，3)。本文选取的样本为泉南高速公路柳州至南宁段共5个边坡监测点获得数据40组。其中训练样本数据30组(稳定20组，变形5组，滑坡5组)，测试样本数据10组(如表1所示)。

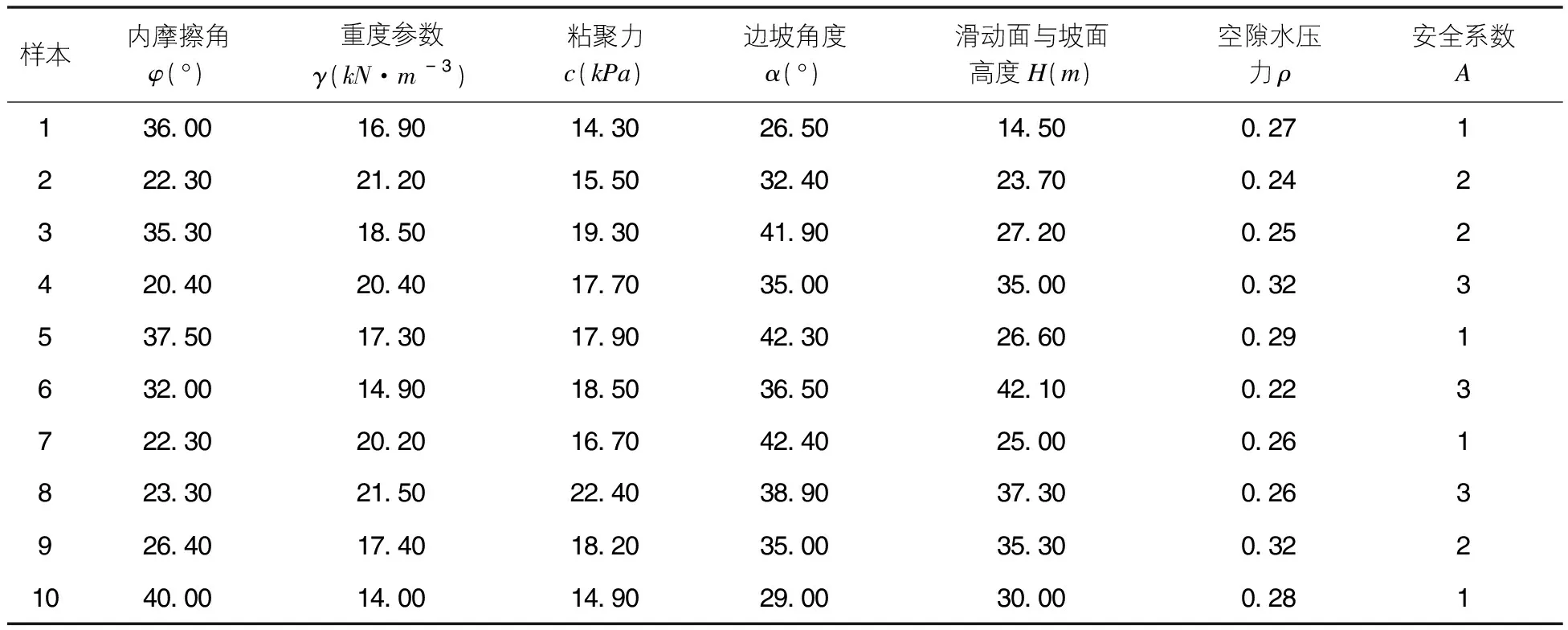
表1 模型测试样本表

因样本组存在奇异性，所以对样本数据进行归一化处理，公式如式(14)所示：

y=(ymax-ymin)·(x-ymin)/(xmax-xmin)+ymin

(14)

3 模型分类测试结果分析

本文使用MATLAB软件中的SVM和ANFIS工具包对边坡监测数据样本进行模拟测试。SVM模型的核函数选择更适合分析复杂非线性分类模型的高斯径向基核函数[7]，该核函数的核半径为1。ANFIS模型分类器采用了6个输入节点、1个输出节点，动量因子选择为0.5，学习效率为0.1，训练模型具有良好的误差收敛性能。使用两种模型对10组数据进行计算预测得到安全系数结果如表2所示，测试结果误差比对如图4所示。

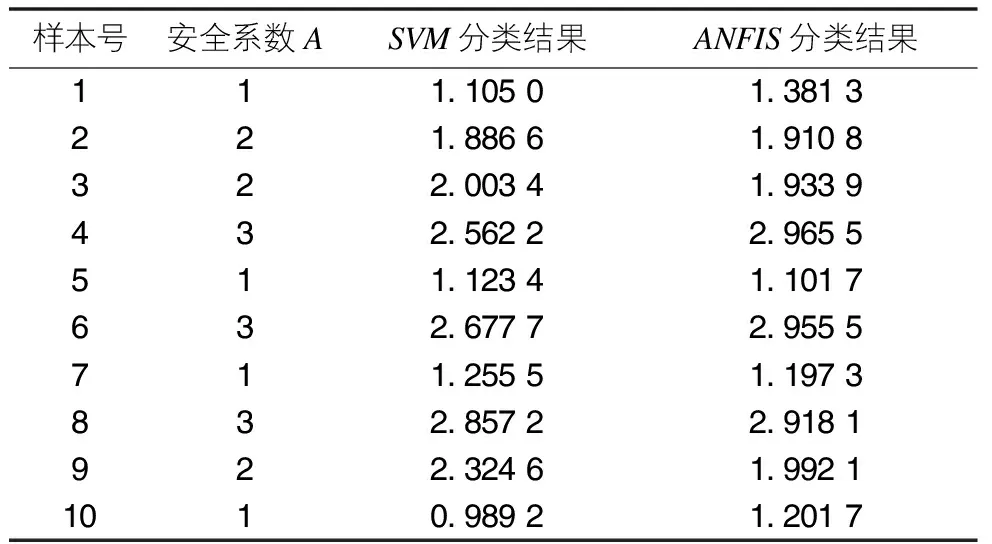
表2 模型分类测试结果比对表

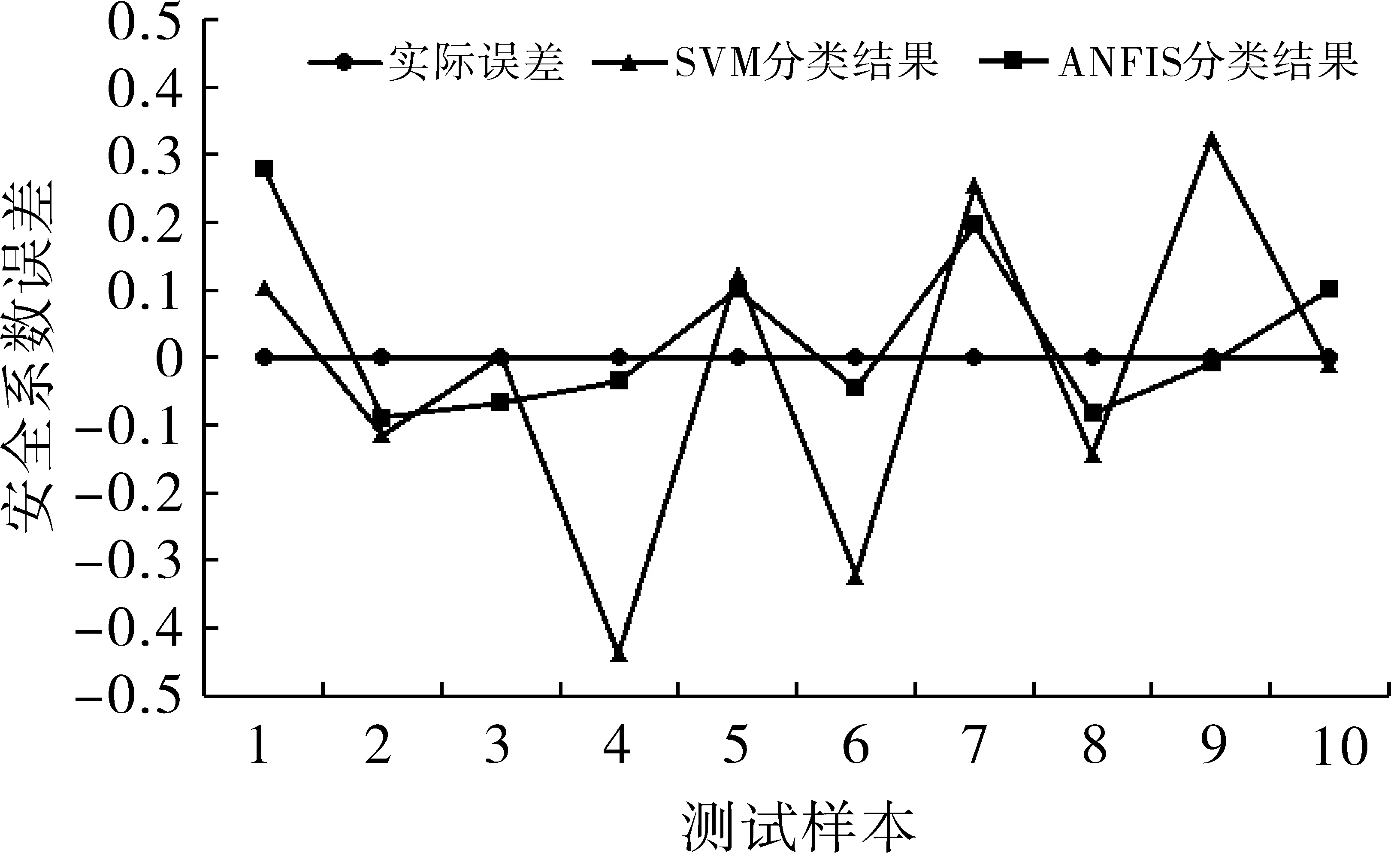
图4 模型测试误差比对示意图

得出SVM分类模型计算预测的安全系数最大误差值为0.437 8，平均误差偏差值为0.186 0；ANFIS分类模型计算预测的安全系数最大误差为0.281 3，平均误差偏差0.107 8。误差分析结果表明，ANFIS分类模型的测试结果比SVM分类模型的测试结果更加接近实际误差，ANFIS分类模型计算预测结果误差有相对较好的收敛性，可获得更为相对准确的安全系数预测结果。

4 结语

本文依托泉南高速公路柳州至南宁段边坡监测项目，针对广西地质条件和气候环境，应用常用的SVM分类模型和ANFIS分类模型，在边坡地质监测数据与边坡安全系数之间建立一种更有效的、误差可收敛的数据计算预测模型，采用30个训练样本组和10个测试样本组进行计算预测，并对其结果进行误差分析比较，得出结论如下：

(1)本文采用非线性分类模型探索边坡地质监测参数与安全系数的相关性，验证了非线性分类模型在边坡监测中应用的有效性。

(2)本文对边坡形变安全系数计算预测，得出ANFIS分类模型可以获得相对更为准确的预测结果。

(3)本文仅对广西的地质和气候条件进行测试，不同区域的地质类型和气候条件下，计算预测结果可能存在较大差异性，后续需探究其他分类模型和监测参数的适宜性。