考虑支座摩阻的半漂浮体系斜拉桥模型修正

陈彦铭,朱利明,邢世玲,徐 松,陈 亮

(南京工业大学,南京 210009)

斜拉桥计算图式较为复杂，模拟计算的边界条件与桥梁实际状态的不同，可能会导致荷载试验计算结果出现偏差。对于半漂浮体系斜拉桥，建立模型时一般不设纵向水平约束，然而大跨度桥梁恒载大，其支座反力也较大，因此不能忽视支座摩阻力的影响。张惠勤等[1]在济南黄河三桥荷载试验过程中，发现在未考虑支座摩阻的情况下，塔偏实测方向与理论相反。王统宁[2]分别在温度、静风和汽车作用下研究支座摩阻对大跨径缆索承重桥梁梁端位移和转角的影响，指出如果不考虑支座摩阻力会使计算得到的梁端位移过大。颜东煌等[3]研究了车辆荷载作用下不同支座模拟方式对大跨度斜拉桥结构主梁纵向位移及桥塔偏位的影响，得出是否考虑支座摩阻的不同情况下差值可达10 cm级别。根据目前研究发现，支座摩阻对斜拉桥的主梁和主塔纵向位移的影响很大，不考虑支座摩阻力一般会使计算得到的主梁和主塔位移过大，在不同的荷载作用下也会出现因未考虑支座摩阻力，计算位移方向与实测方向相反的情况。

以某半漂浮体系斜拉桥荷载试验为背景，针对试验中出现的有限元模型计算结果与实测结果不一致的情况，采用双折线模型和工程上常规的直接加支座摩阻力这2种方式模拟支座摩阻效应修正有限元模型，通过将修正后模型计算值与实测值对比分析，总结出有效的支座摩阻模拟方法。

1 支座摩阻理论

《公路桥涵设计通用规范》[4](JTG D60—2015)中关于支座摩阻力的描述为：上部结构因温度变化引起的伸长或缩短以及受其他纵向力的作用，活动支座将产生一个方向相反的力，即支座摩阻力。摩阻力的大小取决于上部结构传给支座的反力大小、支座类型以及材料。支座摩阻力标准值F的计算公式为

F=μW

式中，W为作用于活动支座上由上部结构重力产生的效应；μ为支座的摩擦系数。

工程上考虑支座摩阻力的常见做法是根据支座反力和摩擦系数求得支座摩阻力的大小，再参考荷载试验模拟计算得到的主梁位移方向，在主梁上加1个与主梁位移方向相反的力。但这种方法并不能模拟活动支座的滑动—停止判别条件，当梁体与支座间未发生滑动时，支座摩阻力小于最大静摩擦力，因此直接加摩阻力的模拟方式并不准确。

参考现有研究，活动盆式支座的摩擦效应可采用双折线模型进行模拟[5-6]。直接加支座摩阻力和双折线模型这2种模拟方法下，滑动支座单元的力-位移曲线如图1所示。支座双折线模型中，当水平力小于临界摩擦力时，支座存在初始水平刚度Ku，Ku的大小为临界摩擦力与支座屈服位移Uy的比值；当水平力大于临界摩擦力时，发生相对位移，并产生与水平力方向相反的摩阻力。在无硅脂润滑条件下，支座摩擦系数一般取0.05[7]，支座的屈服位移一般取2～3 mm[8-9]。

(a) 直接加支座摩阻力

2 实桥荷载试验结果

2.1 工程概况

某工程主桥采用2×115 m独塔四索面斜拉桥，在小里程侧设1个辅助墩，跨径组成为 (34+81+115)m，总长为230 m。该桥车道为双向八车道，分幅布置，单幅标准桥面全宽为19 m，梁高1.5 m，中央分隔带宽为1.5 m，桥面总宽为39.5 m。主桥结构体系采用半漂浮体系，主塔处梁底设置竖向支座及横向挡块，其余辅助墩及过渡墩墩顶设置竖向支座，全桥不设纵向水平约束。

2.2 初始有限元模型

采用MIDAS Civil 2019软件建立全桥有限元模型，采用梁单元对斜拉桥塔、梁和墩进行模拟，由于该桥主跨跨径不大，非线性效应影响较小，斜拉索采用桁架单元模拟，并采用恩斯特公式[10]计算拉索等效弹性模量(考虑拉索垂度效应)。采用桁架单元对斜拉索进行模拟，根据斜拉桥支座形式，初始模型中仅设竖向和横桥向约束，未设纵向水平约束，斜拉桥初始有限元模型如图2所示。

图2 斜拉桥初始有限元模型

2.3 荷载试验方案

选取荷载试验中某一特征工况进行介绍，该工况试验桥跨为8#～9#墩，桥跨共81m，采用三轴载重汽车进行等效加载，主要试验内容为主梁最大正弯矩及挠度、主塔塔顶和主梁梁端纵向位移。荷载试验控制目标与试验效率如表1所示，荷载试验控制截面与轮位纵向布置如图3所示，主梁应变控制截面测点如图4所示。

表1 荷载试验控制目标与试验效率

图3 荷载试验控制截面与轮位纵向布置(单位：cm)

图4 主梁应变控制截面测点

2.4 荷载试验结果

荷载试验结果如表2所示，其中主梁应变校验系数为0.63～0.79，主梁挠度校验系数为0.74，校验系数均小于1.0，满足《城市桥梁检测与评定技术规范》(CJJ/T 233—2015)的要求。实测主梁梁端纵向位移为-0.79 mm，初始模型计算值为33.52 mm；实测主塔塔顶纵向位移为-9.70 mm，初始模型计算值为23.58 mm。初始模型计算的主梁和主塔纵向位移方向均与实测方向相反，且数值相差较大，校验系数为负，不满足规范要求。

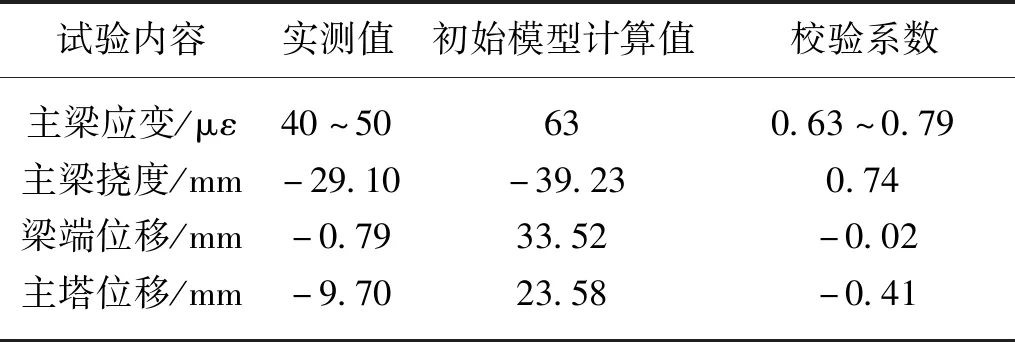
表2 荷载试验结果

3 考虑支座摩阻的有限元模型修正

3.1 有限元模型修正

根据支座摩阻理论，考虑支座摩阻效应对初始模型进行修正，建立4种不同的考虑支座摩阻模型(分别用模型1、模型2、模型3和模型4表示),4种修正模型的摩擦系数均取0.05，模型差别如下。

模型1：直接将支座摩阻力加在主梁上。

模型2：建立双折线模型，支座屈服位移取2 mm。

模型3：建立双折线模型，支座屈服位移取2.5 mm。

模型4：建立双折线模型，支座屈服位移取3 mm。

模型1采取工程上常规的直接加支座摩阻力的模拟方式，提取初始模型中的支座反力，与摩擦系数相乘得到支座摩阻力，根据荷载作用下主梁纵向位移方向，将1个反方向的支座摩阻力加在主梁上。

模型2、模型3和模型4中建立的双折线模型是根据选取的支座摩擦系数和支座屈服位移，在初始模型内梁底单元和墩顶单元间输入如图1(b)所示的力-位移曲线。在midas Civil软件中，可在弹性连接里的变形-内力函数中实现。

3.2 修正模型计算结果分析

分别计算试验荷载作用下4种修正模型的控制截面应变及位移值，与初始模型计算结果和荷载试验实测结果进行比较，各模型计算和实测的荷载试验结果如表3所示。其中，采用校验系数影响系数[η=(修正模型校验系数-初始模型校验系数)×100%]衡量各模型修正方法对荷载试验结果的影响程度，对各试验内容的结果进行分析如下。

表3 各模型计算和实测的荷载试验结果

1) 主梁最大正弯矩

实测主梁控制截面各测点应变数值为40～50 με，初始模型计算值为63 με，初始模型应变校验系数为0.63～0.79。考虑支座摩阻后，修正模型计算应变较初始模型减小，与实测值更接近，4种修正模型计算的应变数值均为52 με左右，应变校验系数为0.76～0.96，比初始模型平均提高约15%。

2) 主梁最大挠度

实测主梁控制截面挠度为-29.10 mm，初始模型计算值为-39.23 mm，初始模型挠度校验系数为0.74。考虑支座摩阻后，修正模型计算挠度值较初始模型减小，与实测值更接近，4种修正模型计算的挠度数值为-30.35～-30.05 mm，挠度校验系数为0.96～0.97，比初始模型平均提高约23%。

3) 主梁梁端纵向位移

实测主梁梁端纵向位移为-0.79 mm，初始模型计算值为33.52 mm，初始模型计算位移方向与实测方向相反且数值相差较大。考虑支座摩阻后，4种修正模型计算的梁端位移方向均与实测方向一致，其中，模型1的计算位移为-2.15 mm，大于实测位移。模型2、模型3和模型4(双折线模型)的计算结果随着支座屈服位移取值的增大呈递增趋势。模型2的计算位移为-0.74 mm，略小于实测值；模型3的计算位移为-0.81 mm，略大于实测值，与实测值最接近。

4) 主梁塔顶纵向位移

实测主梁塔顶纵向位移为-9.70 mm，初始模型计算值为23.58 mm，初始模型计算位移方向与实测方向相反且数值相差较大。考虑支座摩阻后，4种修正模型的塔顶位移方向均与实测方向一致。其中，模型1的计算位移为-11.08 mm，大于实测位移。模型2、模型3和模型4(双折线模型)的计算位移为-9.81～-9.74 mm，均略大于实测值且随着支座屈服位移取值的增大呈递增趋势。

考虑支座摩阻修正模型后，模型计算的应变和挠度数据均更接近实测值，应变和挠度校验系数分别提高了15%和23%，主梁和主塔纵向位移方向也与实测方向一致。模型1(直接加摩阻力)的计算位移结果与实测值相比均偏大，模型2、模型3和模型4(双折线模型)的计算结果与实测值接近，其中模型2(摩擦系数取0.05，屈服位移取2.5 mm)的计算结果与实测数据最吻合。

4 结论

(1) 考虑支座摩阻修正模型后，荷载试验结果较修正前有较大改善，应变和挠度校验系数分别提高了15%和23%，并修正了主梁和主塔纵向位移方向，使之与实测方向一致。

(2) 在支座摩擦系数取0.05的前提下，工程上常规的直接加支座摩阻力的方式因为无法模拟活动支座的滑动—停止判别条件，计算得出的主梁和主塔纵向位移数值普遍大于实测值。而双折线模型的计算结果则与实测值较吻合，建议工程中选用双折线模型模拟支座摩阻效应。

(3) 采用双折线模型模拟支座摩阻效应时，主梁和主塔位移随支座屈服位移取值的增大也呈增大趋势。针对本次试验的斜拉桥，支座摩擦系数取0.05、支座屈服位移取2.5 mm时，有限元模型计算结果与实测值最接近，支座摩擦系数和屈服位移的参数取值可为同类桥梁工程应用提供参考。