基于支路功率的配电网状态估计优化方法

刘汇川，陈曦，王静怡，邵梦虞

（国网江苏省电力有限公司经济技术研究院，江苏 南京210008）

状态估计是一种利用量测数据的相关性和冗余度，应用计算机技术和数学处理的方法对运行参数进行处理，以提高数据的可靠性与完整性，有效获得电力系统实时状态信息的方法[1]。近年来，随着配电系统自动化水平的不断提高，配电网状态估计作为配电自动化系统的基础模块，其算法的收敛性、鲁棒性以及精确度对配电自动化系统和配电网管理系统完成高级分析、控制和调度等功能愈发重要。

由于配电网与输电网在结构、量测配置等方面有较大不同，如：配电网络呈辐射状、三相不平衡、量测冗余度较低、线路R/X较大等。因此，直接将传统的输电系统状态估计方法应用在配电网会出现诸如数值稳定性、信息矩阵不可观测等问题，不能满足工程实际需要。对配电系统的状态估计要求能够处理三相不平衡状况，即进行三相状态估计；能够有效利用辐射状网络结构；能够利用支路电流量测等。

配电系统状态估计较多采用基于支路电气量的方法[1]，文献[2]采用支路电流作为状态量，通过量测变换把各类量测变换成等值的复电流量测从而简化量测矩阵并且实现了三相解耦，在计算时利用配电网辐射状结构，有着与配电系统前推回代潮流计算类似的前推回代过程，简化了计算。但是该方法要求功率量测成对出现且P、Q的权重相同，这在实际工程中很难实现；另外该方法无法利用电压量测，影响了算法的准确度。文献[3]在支路电流法的基础上提出了基于支路功率的配网状态估计方法，该方法通过量测变换，实现了量测函数完全线性化，量测信息矩阵成为常数矩阵，同时P、Q解耦，大大提高计算效率，增强了支路法的实用性。但是，作为对配电网的分析，该算法没有过多考虑配电系统量测配置不足的情况，无法利用支路电流幅值量测和节点电压幅值量测，降低了量测冗余度，从而很容易导致状估结果可信度不高甚至状估计算不可观测的情况。文献[4]推导出了电压电流幅值量测变换公式，并给出了计及全部量测类型的状估计算步骤。但是由于该方法在求取状估初值时只能利用功率量测，在功率量测占比较低数据系统中同样容易出现不可观测的情况，进而无法利用全部量测类型进行状态估计计算。

本文立足于配电网量测配置现状，以提高状态估计的可观测性和准确度为目标，针对实际工程面临的问题，提出一种实用性更强、鲁棒性更高的改进状估方法。本文通过利用节点功率量测和功率伪量测先对电网进行一次前推回代潮流迭代，得到状态估计计算初值，然后利用全部量测类型，通过量测变换，对系统进行状态估计。从根本上避免了在求取状态估计计算初值时出现信息矩阵不可观测的问题，同时可以有效利用全类型量测数据，提高了状估的数值可观测性和计算准确度。

1 状态估计基本原理

状态估计是利用冗余的量测或伪量测数据按照一定的准则来估计系统的真实状态。

量测值与量测真值之间的误差越小，表示估计的状态越准确。基本加权最小二乘状态估计是以计算得到的测量估计值与实际量测值之差的加权平方和最小为目标准则的估计方法。它是许多状态估计算法的基础方法。

在电力系统中，由于量测设备的自身设计、工作环境等因素的不同，其精度往往参差不齐。量测误差越小的数据，在估计过程会使整体结果更精确。所以，有必要对不同精度的数据进行区分，给以不同的权重。

2 量测变换

2.1 量测变换理论

一般的量测函数为非线性函数，若在允许的精度范围内，采用量测变换方法，将实际的量测量变换成与其等值的新的量测量，使得新量测的量测函数为线性函数，这样变换后的量测雅克比矩阵就变为常数矩阵，状态估计问题的计算效率将会显著提高。

2.2 配电系统的量测变换模型

在配电系统中，利用其辐射状结构，采用由首端到末端的支路功率作为状态变量。将电网中实际的功率量测、支路电流幅值量测、节点电压幅值量测统一变换为支路首端等效功率量测，使得变换后的量测雅克比矩阵线性化。

2.2.1 各量测的等效变换

典型配网辐射状结构如图1所示。根据实际量测信息进行量测变换，Pij、Qij表示支路首端功率，Pji、Qji表示支路末端功率，Pm、Qm表示实际量测量，Pme、Qme表示等效量测量，以图中箭头所示方向为正方向。

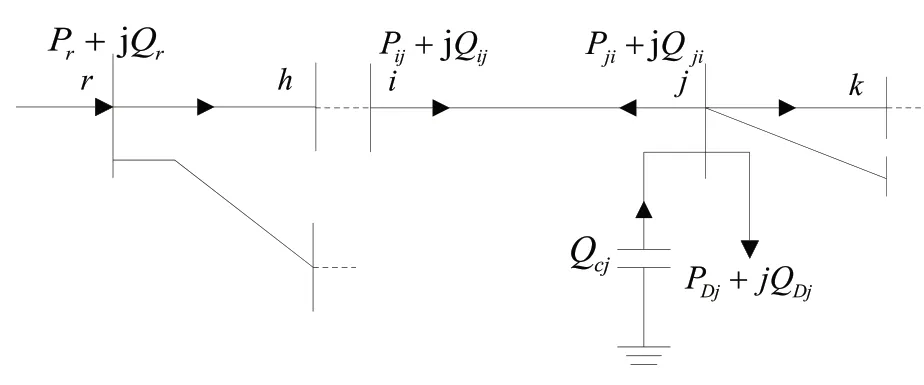
图1 典型辐射状配电网示意图

支路首端功率量测：

支路末端功率量测：

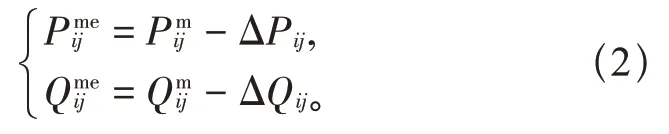
式中：ΔPij、ΔQij为线路Lij的功率损耗，它是状态变量的非线性函数。

负荷功率量测：

根节点注入量测：

电流幅值量测：

式中：为实际支路电流幅值量测；Iij为上一次迭代得到的支路电流幅值估计值。

电压幅值量测：

式中：为实际节点电压幅值量测；Vj为上一次迭代得到的节点电压幅值估计值。

2.2.2 等效量测函数

以支路首端功率作为状态量，经量测变换后的等效量测Z'的量测函数h'分别如下：

支路首端功率等效量测函数：

支路末端功率等效量测函数：

负荷功率等效量测函数：

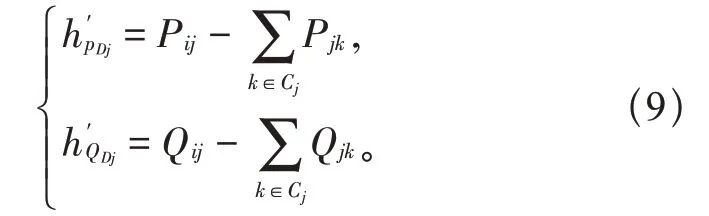
式中：Cj是根节点j的子节点集合。

根节点注入等效量测函数：

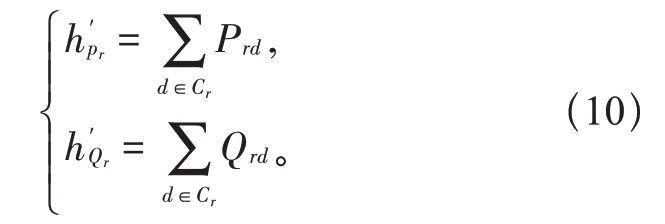
式中：Cr是根节点的子节点集合。

电流幅值等效量测函数：

电压幅值等效量测函数：

2.3 配电系统量测模型在量测变换理论上的表达

由（7）～（12）式可以看到，经过量测变换后，量测函数均为状态量的线性函数；且有功量和无功量实现了解耦：

、是只含有1、-1的稀疏常系数矩阵，当有功量测和无功量测成对出现时，有：=；常向量A′为0。

结合式（1）～（6），可以发现，A(x)为单位阵，因此对于等效量测的权重矩阵W′严格等于实际量测的权重矩阵W。将W分为Wp、WQ，于是得到配电系统等效变换状态估计的迭代式：

其中，等效信息阵：

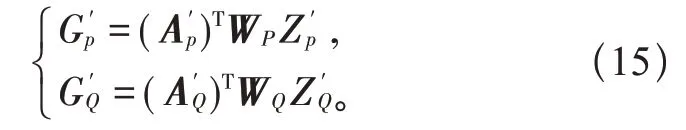
式中：Z为量测向量。

3 算法步骤

3.1 状估初值的获取

基于支路功率的状估算法在进行配电网状态估计时均存在难以利用电流量测的问题，因为初始节点电压幅值相等，导致支路电流的初始计算值为“0”，进而导致第一次迭代时出现无穷大项。在电流量测比重比较大的情况下会造成状估准确度较差甚至数据不可观测，还造成量测量的浪费。如果解决了各节点电压初始值选取的问题，就可以利用全部量测进行状态估计。

可以看到，如何合理地选取状估计算各节点电压的初始幅值，对于进行准确可靠的状估计算十分重要。对此，文献[4]提出只用功率量测先进行一次状估迭代，得到各节点的电压初始值。但是，如果功率量测不足时，仅利用功率量测进行状估依然会出现不可观测的情况，导致后续计算无法进行。因此，本文提出利用节点功率量测和功率伪量测对辐射状电网先进行一次前推回代潮流计算，得到状态变量初值，然后根据等效功率变换的方法利用全部量测类型对系统进行准确的状态估计。

3.2 算法流程

步骤（1）状态估计初始化：包括对网络拓扑分析；添加负荷伪量测和零虚拟负荷量测；根据式（7）～（12）形成系数矩阵、；联立权重矩阵WP、WQ计算信息矩阵、并对其进行因子分解；迭代变量k=0。

步骤（2）根据节点的负荷量测和伪量测对所有节点进行一次前推回代潮流迭代，得到各节点电压和状态量的初始值：

步骤（6）判断相邻两次迭代电压差的模分量的最大值maxΔVi是否小于收敛精度，若是，停止计算；否则，k++跳转步骤(2)。

4 算例分析

本文用C语言编写了改进后的等功率变换状态估计算法，作为比较，同时实现了文献[3]中的算法。本文的算例采用配电系统分析常用算例系统中的33母线系统[1]以及我国某地区实际配电系统的一条183节点出线。对于33母线测试系统的量测配置以及量测值采用文献[4]提出的方法进行量测模拟，以潮流计算解作为真值。

为了对比状态估计的效果，采用文献[4]中给出的量测误差统计值SM和估计误差统计值SE以及目标函数值J(x)作为对比。

4.1 母线系统

系统信息如表1所示。计算结果对比如表2所示。

表1 33母线测试系统信息

由表2可知，两种算法均可以快速收敛。并且，相对于等功率变换的状估方法，本方法的目标函数值优化得更小，而估计误差统计值相对于量测误差统计值也减小得更多，说明估计得到的量测值比量测值更接近于真值。结果证明了本文提出的获取初值的办法是合理有效地。另外，从表1中可以看到，测试系统的量测冗余度较大，说明在量测充裕的系统中，两种方法均能有效地进行状态估计计算，而且都得到了较为理想的状估结果。

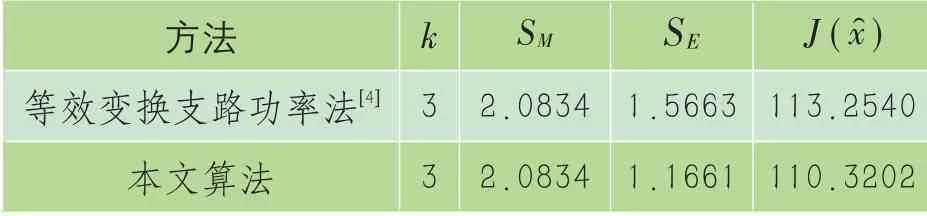
表2 33母线系统计算结果对比

4.2 实际183母线系统

系统信息如表3所示。

计算结果如表4所示。

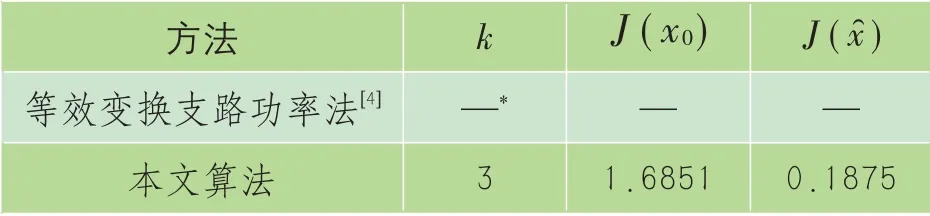
表4 183母线系统计算结果对比

由表3可知，此实际系统的量测配备不足，并且电压电流幅值量测占比重较大，因此需要添加大量的负荷伪量测和零虚拟负荷量测。结合表4的计算结果，可以看出等功率变换的状估方法由于功率量测不足导致状估不可观测。而本文方法能够适应功率量测不足的情况，得到合理的电压初始幅值后，便可以利用全部量测进行状估。算法经过3次迭代就取得收敛，并且通过状估计算目标函数值有了较为显著的下降，可以满足实际应用要求。

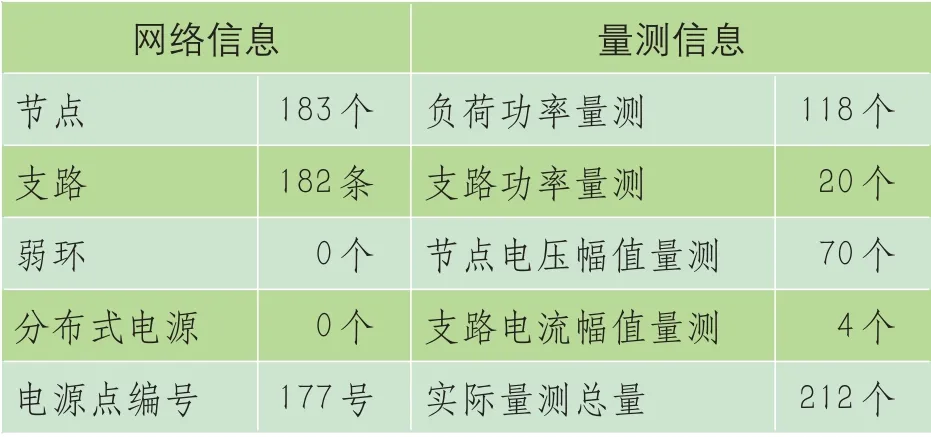
表3 183母线测试系统信息

5 结束语

本文在等效功率变换状估计算方法的基础上，提出了实用性更强的基于支路功率的改进状态估计方法，本方法能够适应实际配电系统中经常遇到的量测冗余度不足、功率量测占比重较低的问题，大大提高了量测系统的可观测性。同时改进方法可以充分利用系统采集到的全类型量测数据，在有限的数据冗余度情况下尽可能提高状态估计准确度。测试算例和实际工程算例均证明，本方法可以有效地解决状态估计问题，具有较强的鲁棒性和实用性。