无缝换乘地铁车站的地震响应特性研究

于仲洋，张鸿儒，邱滟佳，李昊

摘   要：為探究无缝换乘地铁车站的地震响应特性，提高对此类车站结构抗震性能的认识，首先开展此类车站结构缩尺模型的振动台试验. 试验方案设计包括试验模型的制备、试验测点的布设与采集、试验加载工况设计;随后对模型试验过程进行三维有限元数值模拟. 通过对比数值模拟与实测结果，分析模型土的加速度响应规律、结构模型的应变和内力响应规律以及侧墙上的土压力响应规律. 结果表明：数值结果与实测结果吻合较好，验证了本文建模方法的合理性;对于无缝换乘地铁车站结构模型，车站交叉端部对车站结构构件的变形、内力以及周围土层影响明显，而当与车站交叉端部的距离超过1.5倍的车站结构宽度以后，影响基本消失. 上述结论可为复杂地铁车站地震分析的三维计算方法以及此类型车站结构的抗震设计提供有力支持.

关键词：无缝换乘地铁车站;三维数值模拟;振动台试验;地震响应特性;地下结构

中图分类号：TU92;TU435                        文献标志码：A

Study on Seismic Response Characteristics

of a Seamless Exchange Subway Station

YU Zhongyang1，2？覮，ZHANG Hongru1，3，QIU Yanjia1，3，LI Hao1，3

（1. Key Laboratory of Urban Underground Engineering of Ministry of Education，Beijing Jiaotong University，Beijing 100044，China;

2. The First Construction Engineering Company Ltd. of China Construction Second Engineering Bureau，Beijing 100176，China;

3. School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China）

Abstract：To study the seismic response characteristics of the seamless transfer subway station and improve the understanding of the seismic performances of such station structures， the shaking table test on a scale model of such station structure was carried out for  the first time. The design of the shaking table test included the preparation of test models， the arrangement of measuring points， collection of testing data and the design of test working conditions. Then， the processes of the model test were simulated by three-dimensional finite element method. Through comparison between the numerical and measured results， acceleration responses of the model soil， strain and internal force responses of the structure model and soil pressure responses on the sidewall were analyzed. The results showed that the numerical results agreed well with the test data， which validated the rationality of the modeling method in this paper. For the structure model of the seamless exchange subway station， the structural exchange end had an obvious influence on the structural deformation， the structural internal force and its surrounding soils. When the distance between the station exchange ends exceeded 1.5 times station structural width， its effect basically disappeared. These conclusions can provide powerful support to the three-dimensional calculation method for the seismic analysis of complex subway stations and the anti-seismic design of such station structures.

Key words：seamless exchange subway station;three-dimensional numerical simulation;shaking table test;seismic response characteristics;underground structure

随着大城市、特大城市的高速发展，城市轨道交通网络愈发复杂，涌现出了大量的大型复杂地铁车站，如双线换乘、三线换乘地铁车站. 我国位处环太平洋地震带和欧亚地震带之间，70%以上的城市处于地震活动区[1]，因此，对于城市轨道交通的抗震安全性评估和抗震设计已然成为科学研究的重要课题[2]. 近年来各国学者针对城市轨道交通抗震开展了大量的研究，特别是1995年日本阪神大地震，地铁车站的大量损伤破坏使得地下结构抗震得到了越来越多的关注[3-4]. 通过震害实例调查[5-6]、模型试验[7-9]以及数值模拟[10-14]研究，对结构断面形式简单的浅埋地下结构的主要动力反应特性认识基本一致. 地下结构的振动模式主要依赖于周围土层;地下结构的变形由周围土层的变形控制，结构的惯性作用不显著;对于框架式地下结构，中柱是结构的薄弱环节，地下结构的破坏通常是由中柱失效引起的;地下结构构件中材料刚度的过渡区域，如连接段、弯曲段，通常被认为是地下结构地震损伤的关键部位.

然而对于结构断面形式复杂的大型地铁车站，如十字交叉换乘车站、并行通道换乘车站、地下商业区与车站合建结构等，由于其受力特性复杂，除了地下结构与周围土层间动力相互作用外，结构与结构间的动力相互作用也起到至关重要的作用，且其结构模型制作成本高，试验过程困难，因此开展的相关试验研究较少.

袁蕾等[15]以实际工程中换乘地铁车站为例，通过数值模拟的方法分析了不规则结构的侧向变形以及中柱内力等方面的地震特性. 张波等[16]和黄俊等[17]利用数值模拟的方法分析了地铁超近距交叉结构的地震响应特性，并以常见的双隧道下穿单层车站结构为背景进行了振动台试验研究，对比分析了单体车站结构与交叉车站结构的异同. 王国波等[18]利用数值模拟的方法分析了三维的十字换乘车站结构，对比了换乘车站结构的地震响应与单体车站结构的地震响应间的异同，探讨了其空间效应及抗震性能. 于仲洋等[19]以板壳理论为基础，推导了交叉换乘车站结构中交叉部分的影响范围简化模型，并在此基础上提出了交叉换乘车站结构的分步抗震设计思路. 张宇[20]利用数值模拟的方法分析了T型交叉换乘地铁车站结构的地震损伤过程，并通过对比交叉段结构及标准段结构的地震响应特性，证明相互作用特性在此类地铁车站设计中的重要性. 韩学川等[21]基于大开洞连体并行地铁车站的三维有限元模型，在考虑了输入地震动特性以及混凝土结构损失特性等条件下，探究连体并行地铁车站结构非线性地震响应的特性.

综上所述，尽管部分学者对复杂地下结构的地震特性进行过研究，但是对于无缝换乘形式的地铁车站结构的地震特性研究依然较少，且以往研究大部分基于数值模拟的方法，本文则首次通过振动台试验和三维数值模拟两种方法探究无缝换乘地铁车站结构的地震响应特性，包括土层的加速度响应规律、车站结构的应变及内力响应规律，以及结构周围的土压力响应规律. 通过数值模型与实测数据的对比分析，验证本文建模方法的合理性. 通过振动台实测数据结合数值模拟分析，探究此类车站结构交叉端部对车站结构整体抗震性能的影响，为后续此类地铁车站结构的抗震设计奠定基础.

1   振动台模型试验

1.1   试验模型制备

本次试验在中国地震局工程力学所恢先实验室中进行，台面尺寸为5 m×5 m、标准荷载为300 kN、最大倾覆力矩为750 kN·m，剪切模型箱尺寸为3.7 m×2.4 m×1.7 m（长×宽×高）. 文献[22-23]已对模型箱的动力性能、边界效应影响等问题进行测试，证明该模型箱能够有效地完成地下结构的振动台试验.

试验以典型的无缝换乘地铁车站结构为原型，在模型制备过程中对车站结构进行了简化处理，去掉了部分附属结构，实物如图1所示. 模型两个方向的结构断面分别为三层三跨的结构断面和两层三跨的结构断面，模型俯视图呈十字型，总尺寸为2 220 mm×1 600 mm×414 mm（长×宽×高），各断面尺寸如图2所示.

结构模型在制备的过程中充分考虑了振动台设备的限制以及结构模型的整体性，保证结构模型在尽可能满足相似比关系的同时便于加工、制作. 而在小比例缩尺模型试验中，由于钢筋混凝土构件制作复杂且难以保证模型质量，因此选择均质性好、强度高、弹性模量低的有机玻璃作为结构模型的材料. 模型土选取某车站施工现场基坑开挖的重塑土，在装箱完成后对模型土进行不同深度取样，通过室内试验测得土样参数如表1、表2所示.

相似比设计涉及到结构模型和模型土两种材料，在保证结构模型相似比的前提下，需要对模型土施加人工质量才能保证两种材料的相似关系一致，而这将导致土层的动力特性发生明显改变;考虑到试验的目的是探究结构模型的地震响应特性，因此在设计过程中以结构模型的相似关系为主，并允许模型土的一些非关键相似比失真.

选择长度、弹性模量和加速度作为结构模型的基本物理量，剪切波速、密度和加速度作为模型土的基本物理量，根据相似率原理[24]，模型相似比关系如表3所示. 另外，为弥补缩尺模型在质量上的损失，对结构模型进行合理配重，配重计算公式为：m配重 = L2rEr m原型 - m模型;经换算得到模型底层配重为361.6 kg、其余每层配重为542.4 kg.

1.2   测点布设与数据采集

采集数据包括模型土层中的加速度响应、结构模型的应变响应以及结构模型侧墙上的土压力响应. 试验共设置7个应变观测断面，每个断面设置10个测点，分别测试结构侧墙的顶部、中部、底部以及中柱的顶部、底部的应变响应;应变片传感器的电阻值为（120±0.2） Ω，用字母S表示，共计70个. 设置一个加速度观测轴面，测试模型土从底到顶的加速度响应分布. 加速度传感器直径13.2 mm，厚度23 mm，工作频率1～10 000 Hz，电压灵敏度10 mV/g，用字母A表示，共计9个. 设置一个土压力水平观测軸面，测试结构模型表明的土压力响应沿水平方向分布;土压力盒传感器直径28 mm，厚度10 mm，量程0～50 kPa，灵敏度0.5% F.S（Full Scale），用字母P表示，共计6个. 在试验前对各类传感器进行测试与校正，具体测点布置如图3所示.

1.3   试验加载工况

试验工况采用三条频谱特性差异明显的地震波记录，三条地震波强震部分的加速度时程曲线以及其傅氏谱如图4所示.

虽然振动台试验是一个损伤累积的过程，但是也应该尽量保证每组工况初始条件的一致性. 因此，试验加载过程均采用X单向输入，输入地震动的强度从0.1g ～0.6g逐级加载，具体加载工况如表4所示.

2   三维建模

2.1   模型参数

有限元模型中各部分尺寸与模型试验中各部分尺寸一致. 由于有机玻璃材料强度高，试验过程中并没有产生破坏，因此采用线弹性本构关系模型描述结构模型的特性，参数如表5所示. 采用摩尔库伦模型描述土层性质，各工况中的土层参数均由相应工况的共振柱试验拟合得到，如表1、表2所示. 利用瑞利阻尼模型描述土层的阻尼性质，瑞利阻尼参数的计算公式为ξi=（α+βw2i）/2wi，其中，ξi为阻尼比，wi为自振周期，α为质量阻尼系数，β为刚度阻尼系数[25].

2.2   有限元模型

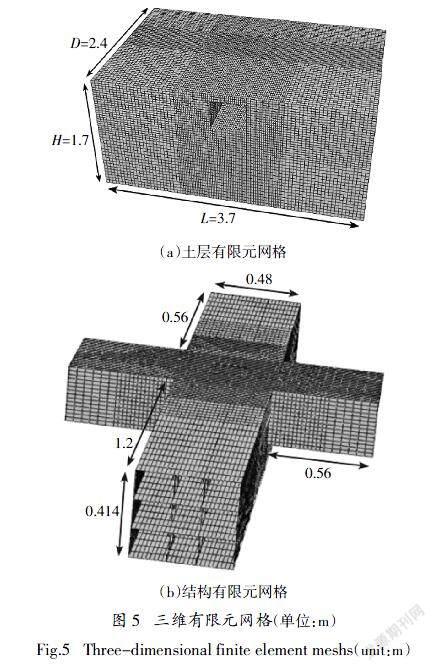
有限元模型的建立参考了文献[25-26]中的方法，采用ABAQUS中C3D8R实体单元模拟土层介质，S4R壳单元模拟原型车站结构. 土层介质的最宽网格尺寸取0.05 m，且距离结构越近，网格越密集，三维模型网格如图5所示. 考虑模型土与结构间的相互作用，采用ABAQUS中“主从面”模拟土与结构间的接触效应，法向采用“硬”接触，切向采用摩擦接触，摩擦系数取0.4[27].

地震动输入方向与试验方向一致. 研究表明，选用试验采集的数据作为模型侧边界可以很好地还原试验结果[28]. 因此，模型底面边界竖向固定，在侧向边界外添加弹簧阻尼器后再添加试验数据，换算得到的应力边界条件，弹簧和阻尼参数选取方法与文献[19]中的方法一致.

法向边界：KBN = αN■，CBN = ρcp      （1）

切向边界：KBT = αT■，CBT = ρcs   （2）

式中：KBN、KBT分别为弹簧的法向刚度与切向刚度;CBN、CBT分别为阻尼的法向与切向参数;R、G、ρ分别为结构与人工边界点的距离、剪切模量和质量密度;cs、cp分别为S波和P波波速;αN、αT分别为法向与切向粘弹性人工边界参数，αN取4/3，αT取2/3[29-30].

3   计算结果与分析

以模型试验和数值模拟计算结果为基础，首先，通过对比分析验证本文建模方法的合理性;随后，利用两部分的计算结果探究此类车站结构与周围土层间以及车站自身结构间复杂的动力相互作用.

3.1   加速度响应对比分析

以工况2、工况10为例，提取模型顶部测点A8的试验实测与数值计算结果，整理测点的加速度时程曲线和傅氏谱分别如图6、图7所示，其余测点（除去损坏测点）的峰值加速度及加速度放大系数如表6所示.

对比图6和图7中曲线可知，数值模拟与试验实测得到的波形和振幅数据吻合较好，傅氏谱的频谱分布也非常相似. 其余工况计算结果均与图6和图7中结果类似，受篇幅限制此处不再一一列举. 综合对比，认为本文的建模方法很好地还原了振动台试验过程，能够有效模拟不同工况条件下土层的加速度响应规律.

另外，由表6数据可以发现，模型顶部测点的加速度响应幅值大于模型底部的加速度响应幅值，该现象证实了场地的放大效应. 而随着地震动强度的增大，场地的加速度放大系数反而减小，该现象是由于地震动强度增大导致模型土的阻尼增大（见表2），从而削弱了场地的放大效应.

3.2   结构应变响应对比分析

使用半桥接法采集结构应变数据，结构构件内外两侧测点反映一个应变值. 分析对象位置如图8所示，分别为地下二层的侧墙底部测点（图中为侧墙交叉处）和地下三层的中柱底部测点.

受篇幅限制，应变时程曲线仅列举测点S3-S4在工况4下的实测数据，如图9所示. 整理分析对象在其他工况条件下的应变响应峰值，以工况2、工况10为例，侧墙和中柱应变响应峰值沿水平方向的变化趋势如图10所示.

由图10可知，两种方法作用下得到的曲线幅值和趋势基本一致，再次证明了本文建模方法的合理性. 另外，尽管地下结构的地震反应在很大程度上取决于输入地震动特性，但是对于本文探究的车站结构形式，车站交叉换乘端部对结构自身内力的影响受输入地震动的影响较小. 在工况2、工况10作用下，车站结构的侧墙和中柱应变响应结果最终均在0.5～0.6 m内变化并趋于稳定.若以车站结构宽度作为计量单位，可认为此类车站交叉换乘端部的影响范围基本在1.5倍的车站结构宽度以内.

3.3   結构构件内力分析

为了进一步探讨无缝换乘地铁车站结构的变形和内力响应特征，揭示此类车站两个方向的结构间的动力相互作用模式，给出车站交叉端部的影响范围，进行了数值模型的结构内力分析. 提取纵向的三层车站结构侧墙的弯矩、剪力和中柱弯矩、轴力值，相应的内力响应沿水平方向的变化曲线，如图11所示.

由图11可知，不同工况条件下结构侧墙顶部均出现弯矩减小，剪力增大的现象，相比于远端构件弯矩平均减小了74.7%，剪力平均提高了381.5%;侧墙交叉处受交叉端部的影响，弯矩和剪力相应地平均增大了111.3%和94.1%;而侧墙底部弯矩平均增大了13.2%，剪力平均减小了35.9%.这是此类无缝换乘地铁车站特有的结构形式造成的，相比于单体地铁车站，此类车站由于横向两层换乘结构的存在，大幅度提高了车站交叉换乘段上部结构的整体刚度，因此，在地震作用下车站交叉换乘段的顶层、中层结构整体变形，弯矩较小;而车站交叉换乘段的底层由于缺少横向结构，水平抗弯刚度骤减，因此在结构侧墙的交叉处出现了结构变形、弯矩增大的现象. 中柱弯矩的变化趋势和产生原因均与侧墙部分类似，中柱的轴力在车站交叉端部附近提高了近50%，主要是由于车站交叉换乘段附近的结构中柱需要承受两个方向的上部荷载，因此中柱轴力显著提高. 另外，随着与车站交叉端部距离的增加，车站各部分结构构件的内力变化最终均在0.5～0.6 m内趋于稳定，由此可认为当距离超过该范围后，车站结构内力基本不再受交叉端部的影响.

上述现象揭示该类型车站两个方向的结构间的动力相互作用模式，综合对比各曲线可以发现，此类车站结构模型的交叉端部对车站结构整体的抗震性能影响显著，尤其是车站的交叉换乘段，由于是结构刚度的过渡区域，因此会在结构底层产生极大的变形. 与此同时，此类换乘地铁车站的交叉端部对车站结构整体的影响存在一定范围，且该影响范围主要受自身结构特性的影响. 对于本文探究的无缝换乘地铁车站结构模型，该影响范围为1.5倍的车站结构宽度，此结论与文献[19]中理论简化模型推导的结论一致，从另一个角度也证明了本文中数值分析的可靠性.

3.4   侧墙土压力分析

3.3节利用数值分析探究此类车站两个方向的结构间的动力相互作用模式，本节利用模型试验进一步探究此类车站与周围土层间的复杂动力相互作用模式.

本次试验在结构模型侧墙的同一高度沿水平方向布置6个土压力盒，如图3（a）所示. 不同工况条件下侧墙上的土压力响应峰值沿水平方向的变化曲线如图12所示. 由图12可知，结构模型附近的土层受车站交叉端部的影响明显，在不同地震波、地震动强度作用下，交叉端附近的土压力相比于远端的土压力平均提高了2.21倍. 这些现象主要是由于交叉端对周围土层的约束作用造成的，越靠近交叉換乘区域，结构另一方向的约束效果越强，交叉点附近的土压力也越大. 而且车站交叉端部对结构周围土压力的影响与其对车站结构内力的影响类似，均存在一定的影响范围，当测点距离车站交叉端部超过0.5～0.6 m后，土压力响应幅值几乎再无变化. 由此可见，无缝换乘地铁车站结构与周围土层间的动力相互作用的影响范围与3.3节中结论类似，车站交叉端部对周围土层的影响范围基本在1.5倍的车站结构宽度内，上述范围可认为是此无缝换乘地铁车站结构模型的影响范围.

综上所述，本文采用的数值分析方法可为后续复杂地下结构的三维建模计算提供参考，而确定的车站交叉端部的影响范围可应用到此类车站的抗震设计中，如以车站交叉端部的影响范围为界限，将车站结构的抗震设计分割为两部分，对于超出影响范围部分的地下结构按照传统方法设计，对于影响范围内的地下结构进行单独设计.

4   结   论

利用振动台模型试验近似地还原了无缝换乘地铁车站结构的地震过程，详细地介绍了试验方案的设计部分，并对试验过程进行了三维有限元的数值模拟，得到如下结论：

1）通过对比有限元数值模拟和模型试验两者的计算结果，证明本文采用的建模方法的合理性，也为后续复杂地下结构的三维地震分析方法提供借鉴.

2）通过数值模拟和试验实测结果，揭示无缝换乘车站两个方向的结构间以及结构与周围土层间的复杂动力相互作用，探究此类车站结构模型的交叉端部的影响. 结果表明：本文探究的无缝换乘地铁车站结构模型，受车站交叉端部影响明显，车站交叉端对结构构件内力以及周围土压力的影响存在相似的影响范围，基本在1.5倍的车站结构宽度以内.

上述结论为了解无缝换乘地铁车站结构的地震特性以及后续复杂地下结构的抗震研究提供了有力支持.

参考文献

[1]    王理，徐伟，王静爱. 中国历史地震活动时空分异[J]. 北京师范大学学报（自然科学版），2003，39（4）：544—550.

WANG L，XU W，WANG J A. The saptio-temporal pattern of historical earthquake disaster in China[J]. Journal of Beijing Normal University （Natural Science），2003，39（4）：544—550.  （In Chinese）

[2]    《中国公路学报》编辑部. 中国隧道工程学术研究综述·2015[J]. 中国公路学报，2015，28（5）：1—65.

Editorial Department of China Highway and Transport. Review on China's tunnel engineering research：2015[J]. China Journal of Highway and Transport，2015，28（5）：1—65. （In Chinese）

[3]    UENISHI K，SAKURAI S. Characteristic of the vertical seismic waves associated with the 1995 Hyogo-Ken Nanbu （Kobe），Japan earthquake estimated from the failure of the Daikai Underground Station[J]. Earthquake Engineering & Structural Dynamics，2000，29（6）：813—821.

[4]    HUO H，BOBET A，FERN？魣NDEZ G，et al. Load transfer mechanisms between underground structure and surrounding ground：evaluation of the failure of the Daikai station[J]. Journal of Geotechnical and Geoenvironmental Engineering，2005，131（12）：1522—1533.

[5]    WANG W L，WANG T T，SU J J，et al. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake[J]. Tunnelling and Underground Space Technology，2001，16（3）：133—150.

[6]    李天斌. 汶川特大地震中山岭隧道变形破坏特征及影响因素分析[J]. 工程地质学报，2008，16（6）：742—750.

LI T B. Failure characteristics and influence factor analysis of mountain tunnels at epicenter zones of great Wenchuan earthquake[J]. Journal of Engineering Geology，2008，16（6）：742—750. （In Chinese）

[7]    陶连金，王沛霖，边金. 典型地铁车站结构振动台模型试验[J]. 北京工业大学学报，2006，32（9）：798—801.

TAO L J，WANG P L，BIAN J. A shaking table test method on the representative subway station structure[J]. Journal of Beijing University of Technology，2006，32（9）：798—801.   （In Chinese）

[8]    CHEN S，ZHUANG H Y，QUAN D Z，et al. Shaking table test on the seismic response of large-scale subway station in a loess site：a case study[J]. Soil Dynamics and Earthquake Engineering，2019，123：173—184.

[9]    ZHUANG H Y，WANG X，MIAO Y，et al. Seismic responses of a subway station and tunnel in a slightly inclined liquefiable ground through shaking table test [J]. Soil Dynamics and Earthquake Engineering，2019，116：371—385.

[10]  郭靖，陈健云. 均质地基地铁车站对临近建筑层间位移角的影响[J]. 湖南大学学报（自然科学版），2013，40（8）：40—45.

GUO J，CHEN J Y. Influence of subway station buried in homogeneous foundations on the inter-story drift ratio of adjacent structures [J]. Journal of Hunan University （Natural Sciences），2013，40（8）：40—45. （In Chinese）

[11]  刘春晓，陶连金，边金，等.可液化土层的位置对土层-地下结构地震反应的影响[J]. 湖南大学学报（自然科学版），2017，44（5）：143—156.

LIU C X，TAO L J，BIAN J，et al. Research on seismic response of the soil and underground structure caused by liquefiable soil in different positions [J]. Journal of Hunan University （Natural Sciences），2017，44（5）：143—156. （In Chinese）

[12]  CHEN Z Y，LIU Z Q. Effects of central column aspect ratio on seismic performances of subway station structures [J]. Advances in Structural Engineering，2018，21（1）：14—29.

[13]  MA C，LU D，DU X，et al. Effect of buried depth on seismic response of rectangular underground structures considering the influence of ground loss [J]. Soil Dynamics and Earthquake Engineering，2018，106：278—297.

[14]  XU Z G，DU X L，XU C S，et al. Numerical research on seismic response characteristics of shallow buried rectangular underground structure[J]. Soil Dynamics and Earthquake Engineering，2019，116：242—252.

[15]  袁蕾，姜忻良. 地鐵换乘站不规则结构对其地震响应的影响[J]. 地震工程与工程振动，2011，31（1）：74—79.

YUAN L，JIANG X L. Influence of irregular structure of subway transfer station on its seismic responses [J]. Journal of Earthquake Engineering and Engineering Vibration，2011，31（1）：74—79. （In Chinese）

[16]  张波，陶连金，姜峰，等. 地铁超近距交叉结构在水平地震荷载下的响应影响分析[J]. 铁道建筑，2011，11：47—50.

ZHANG B，TAO L J，JIANG F，et al. The subway super macro cross structure response under horizontal seismic load impact analysis [J]. Railway Engineering，2011，11：47—50. （In Chinese）

[17]  黄俊，张波. 地铁交叉结构近场地震反应振动台试验研究[J]. 水电能源科学，2013，31（2）：120-122.

HUANG J，ZHANG B. Shaking table model test of subway cross-structure under near-field ground motion [J]. Water Resources and Power，2013，31（2）：120—122. （In Chinese）

[18]  王国波，余淼坤，袁明智，等. 十字换乘地铁车站结构地震响应分析[J]. 岩土工程学报，2019，41（7）：1227—1234.

WANG G B，YU M K，YUAN M Z，et al. Seismic response analysis of cross metro transfer station structure [J]. Chinese Journal of Geotechnical Engineering，2019，41（7）：1227—1234. （In Chinese）

[19]  于仲洋，张鸿儒. 交叉换乘地铁车站地震特性及其设计方法[J]. 东南大学学报（自然科学版），2019，49（5）：1011—1018.

YU Z Y，ZHANG H R. Seismic characteristics and design method for cross transfer subway stations[J]. Journal of Southeast University （Natural Science Edition），2019，49（5）：1011—1018. （In Chinese）

[20]  张宇. T型交叉换乘车站地震反应和损伤分析 [D]. 北京：北京交通大学，2017：64—69

ZHANG Y. The analysis of seismic response and damage of T-shaped transfer station [D].Beijing：Beijing Jiaotong University，2017：64—69. （In Chinese）

[21]  韩学川，陶連金，刘春晓，等. 连体并行地铁车站结构地震响应分析[J]. 北京工业大学学报，2020，46（8）：929—939.

HAN X C，TAO L J，LIU C X，et al. Analysis of influencing factors of seismic response of connected parallel subway stations[J]. Journal of Beijing University of Technology，2020，46（8）：929—939. （In Chinese）

[22]  孙海峰，景立平，王宁伟，等. 振动台多功能叠层剪切箱研制[J]. 岩石力学与工程学报，2011，30（12）：2498—2506.

SUN H F，JING L P，WANG N W，et al. Development of multifunctional laminar shear container for shaking table test[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30（12）：2498—2506. （In Chinese）

[23]  孙海峰，景立平，王树伟，等. 地下结构地震破坏机制试验研究[J]. 岩石力学与工程学报，2013，32（S2）：3627—3635.

SUN H F，JING L P，WANG S W，et al. Experimental study of seismic failure mechanism of underground structure[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32（S2）：3627—3635. （In Chinese）

[24]  林皋，朱彤，林蓓. 结构动力模型试验的相似设计[J]. 大连理工大学学报，2000，40（1）：l—8.

LIN G，ZHU T，LIN B. Similarity technique for dynamic structural model test [J]. Journal of Dalian University of Technology，2000，40（1）：1—8. （In Chinese）

[25]  景立平，孟宪春，孙海峰，等. 三层地铁车站振动台试验的数值模拟[J]. 地震工程与工程振动，2012，32（1）：98—105.

JING L P，MENG X C，SUN H F，et al. Numerical simulation of three-story subway station shaking table test[J].  Journal of Earthquake Engineering and Engineering Vibration，2012，32（1）：98—105. （In Chinese）

[26]  孟宪春. 多层地铁车站振动台试验与数值模拟[D].  哈尔滨：中国地震局工程力学研究所，2011：17—58.

MENG X C. Shaking table test and numerical simulation of Muti-story subway station[D].  Harbin：Institute of Engineering Mechanics，CEA，2011：17—58. （In Chinese）

[27]  庄海洋，王雪剑，王瑞，等. 土-地铁动力相互作用体系侧向变形特征研究[J]. 岩土工程学报，2017，39（10）：1761—1769.

ZHUANG H Y，WANG X J，WANG R，et al. Characteristics of lateral deformation of soil-subway dynamic interaction system[J]. Chinese Journal of Geotechnical Engineering，2017，39（10）：1761—1769. （In Chinese）

[28]  杨林德，王国波，郑永来，等. 地铁车站接头结构振动台模型试验及地震响应的三维数值模拟[J]. 岩土工程学报，2007，29（12）：1892—1898.

YANG L D，WANG G B，ZHENG Y L，et al. Shaking table tests on subway station joint structure and 3D numerical simulation of seismic response [J]. Chinese Journal of Geotechnical Engineering，2007，29（12）：1892—1898. （In Chinese）

[29]  DEEKS A J，RANDOLPH M F. Axisymmetric time-domain transmitting boundaries [J]. Journal of Engineering Mechanics，1994，120（1）：25—42.

[30]  劉晶波，王振宇，杜修力，等. 波动问题中的三维时域黏弹性人工边界[J]. 工程力学，2005，22（6）：46—51.

LIU J B，WANG Z Y，DU X L，et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems [J]. Engineering Mechanics，2005，22（6）：46—51. （In Chinese）